Functional Programming in Scala (2015)
Part 2. Functional design and combinator libraries
We said in chapter 1 that functional programming is a radical premise that affects how we write and organize programs at every level. In part 1, we covered the fundamentals of FP and saw how the commitment to using only pure functions affects the basic building blocks of programs: loops, data structures, exceptions, and so on. In part 2, we’ll see how the assumptions of functional programming affect library design.
We’ll create three useful libraries in part 2—one for parallel and asynchronous computation, another for testing programs, and a third for parsing text. There won’t be much in the way of new syntax or language features, but we’ll make heavy use of the material already covered. Our primary goal isn’t to teach you about parallelism, testing, and parsing. The primary goal is to help you develop skill in designing functional libraries, even for domains that look nothing like the ones here.
This part of the book will be a somewhat meandering journey. Functional design can be a messy, iterative process. We hope to show at least a stylized view of how functional design proceeds in the real world. Don’t worry if you don’t follow every bit of discussion. These chapters should be like peering over the shoulder of someone as they think through possible designs. And because no two people approach this process the same way, the particular path we walk in each case might not strike you as the most natural one—perhaps it considers issues in what seems like an odd order, skips too fast, or goes too slow. Keep in mind that when you design your own functional libraries, you get to do it at your own pace, take whatever path you want, and, whenever questions come up about design choices, you get to think through the consequences in whatever way makes sense for you, which could include running little experiments, creating prototypes, and so on.
There are no right answers in functional library design. Instead, we have a collection of design choices, each with different trade-offs. Our goal is that you start to understand these trade-offs and what different choices mean. Sometimes, when designing a library, we’ll come to a fork in the road. In this text we may, for pedagogical purposes, deliberately make a choice with undesirable consequences that we’ll uncover later. We want you to see this process first-hand, because it’s part of what actually occurs when designing functional programs. We’re less interested in the particular libraries covered here in part 2, and more interested in giving you insight into how functional design proceeds and how to navigate situations that you will likely encounter. Library design is not something that only a select few people get to do; it’s part of the day-today work of ordinary functional programming. In these chapters and beyond, you should absolutely feel free to experiment, play with different design choices, and develop your own aesthetic.
One final note: as you work through part 2, you may notice repeated patterns of similar-looking code. Keep this in the back of your mind. When we get to part 3, we’ll discuss how to remove this duplication, and we’ll discover an entire world of fundamental abstractions that are common toall libraries.
Chapter 7. Purely functional parallelism
Because modern computers have multiple cores per CPU, and often multiple CPUs, it’s more important than ever to design programs in such a way that they can take advantage of this parallel processing power. But the interaction of programs that run with parallelism is complex, and the traditional mechanism for communication among execution threads—shared mutable memory—is notoriously difficult to reason about. This can all too easily result in programs that have race conditions and deadlocks, aren’t readily testable, and don’t scale well.
In this chapter, we’ll build a purely functional library for creating parallel and asynchronous computations. We’ll rein in the complexity inherent in parallel programs by describing them using only pure functions. This will let us use the substitution model to simplify our reasoning and hopefully make working with concurrent computations both easy and enjoyable.
What you should take away from this chapter is not only how to write a library for purely functional parallelism, but how to approach the problem of designing a purely functional library. Our main concern will be to make our library highly composable and modular. To this end, we’ll keep with our theme of separating the concern of describing a computation from actually running it. We want to allow users of our library to write programs at a very high level, insulating them from the nitty-gritty of how their programs will be executed. For example, towards the end of the chapter we’ll develop a combinator, parMap, that will let us easily apply a function f to every element in a collection simultaneously:
val outputList = parMap(inputList)(f)
To get there, we’ll work iteratively. We’ll begin with a simple use case that we’d like our library to handle, and then develop an interface that facilitates this use case. Only then will we consider what our implementation of this interface should be. As we keep refining our design, we’ll oscillate between the interface and implementation as we gain a better understanding of the domain and the design space through progressively more complex use cases. We’ll emphasize algebraic reasoning and introduce the idea that an API can be described by an algebra that obeys specificlaws.
Why design our own library? Why not just use the concurrency primitives that come with Scala’s standard library in the scala.concurrent package? This is partially for pedagogical purposes—we want to show you how easy it is to design your own practical libraries. But there’s another reason: we want to encourage the view that no existing library is authoritative or beyond reexamination, even if designed by experts and labeled “standard.” There’s a certain safety in doing what everybody else does, but what’s conventional isn’t necessarily the most practical. Most libraries contain a lot of arbitrary design choices, many made unintentionally. When you start from scratch, you get to revisit all the fundamental assumptions that went into designing the library, take a different path, and discover things about the problem space that others may not have even considered. As a result, you might arrive at your own design that suits your purposes better. In this particular case, our fundamental assumption will be that our library admits absolutely no side effects.
We’ll write a lot of code in this chapter, largely posed as exercises for you, the reader. As always, you can find the answers in the downloadable content that goes along with the book.
7.1. Choosing data types and functions
When you begin designing a functional library, you usually have some general ideas about what you want to be able to do, and the difficulty in the design process is in refining these ideas and finding a data type that enables the functionality you want. In our case, we’d like to be able to “create parallel computations,” but what does that mean exactly? Let’s try to refine this into something we can implement by examining a simple, parallelizable computation—summing a list of integers. The usual left fold for this would be as follows:
def sum(ints: Seq[Int]): Int =
ints.foldLeft(0)((a,b) => a + b)
Here Seq is a superclass of lists and other sequences in the standard library. Importantly, it has a foldLeft method.
Instead of folding sequentially, we could use a divide-and-conquer algorithm; see the following listing.
Listing 7.1. Summing a list using a divide-and-conquer algorithm

We divide the sequence in half using the splitAt function, recursively sum both halves, and then combine their results. And unlike the foldLeft-based implementation, this implementation can be parallelized—the two halves can be summed in parallel.
The importance of simple examples
Summing integers is in practice probably so fast that parallelization imposes more overhead than it saves. But simple examples like this are exactly the kind that are most helpful to consider when designing a functional library. Complicated examples include all sorts of incidental structure and extraneous detail that can confuse the initial design process. We’re trying to explain the essence of the problem domain, and a good way to do this is to start with trivial examples, factor out common concerns across these examples, and gradually add complexity. In functional design, our goal is to achieve expressiveness not with mountains of special cases, but by building a simple and composable set of core data types and functions.
As we think about what sort of data types and functions could enable parallelizing this computation, we can shift our perspective. Rather than focusing on how this parallelism will ultimately be implemented and forcing ourselves to work with the implementation APIs directly (likely related to java.lang.Thread and the java.util.concurrent library), we’ll instead design our own ideal API as illuminated by our examples and work backward from there to an implementation.
7.1.1. A data type for parallel computations
Look at the line sum(l) + sum(r), which invokes sum on the two halves recursively. Just from looking at this single line, we can see that any data type we might choose to represent our parallel computations needs to be able to contain a result. That result will have some meaningful type (in this case Int), and we require some way of extracting this result. Let’s apply this newfound knowledge to our design. For now, we can just invent a container type for our result, Par[A] (for parallel), and legislate the existence of the functions we need:
· def unit[A](a: => A): Par[A], for taking an unevaluated A and returning a computation that might evaluate it in a separate thread. We call it unit because in a sense it creates a unit of parallelism that just wraps a single value.
· def get[A](a: Par[A]): A, for extracting the resulting value from a parallel computation.
Can we really do this? Yes, of course! For now, we don’t need to worry about what other functions we require, what the internal representation of Par might be, or how these functions are implemented. We’re simply reading off the needed data types and functions by inspecting our simple example. Let’s update this example now.
Listing 7.2. Updating sum with our custom data type

We’ve wrapped the two recursive calls to sum in calls to unit, and we’re calling get to extract the two results from the two subcomputations.
The problem with using concurrency primitives directly
What of java.lang.Thread and Runnable? Let’s take a look at these classes. Here’s a partial excerpt of their API, transcribed into Scala:

Already, we can see a problem with both of these types—none of the methods return a meaningful value. Therefore, if we want to get any information out of a Runnable, it has to have some side effect, like mutating some state that we can inspect. This is bad for compositionality—we can’t manipulate Runnable objects generically since we always need to know something about their internal behavior. Thread also has the disadvantage that it maps directly onto operating system threads, which are a scarce resource. It would be preferable to create as many “logical threads” as is natural for our problem, and later deal with mapping these onto actual OS threads.
This kind of thing can be handled by something like java.util.concurrent .Future, ExecutorService, and friends. Why don’t we use them directly? Here’s a portion of their API:
class ExecutorService {
def submit[A](a: Callable[A]): Future[A]
}
trait Future[A] {
def get: A
}
Though these are a tremendous help in abstracting over physical threads, these primitives are still at a much lower level of abstraction than the library we want to create in this chapter. A call to Future.get, for example, blocks the calling thread until the ExecutorService has finished executing it, and its API provides no means of composing futures. Of course, we can build the implementation of our library on top of these tools (and this is in fact what we end up doing later in the chapter), but they don’t present a modular and compositional API that we’d want to use directly from functional programs.
We now have a choice about the meaning of unit and get—unit could begin evaluating its argument immediately in a separate (logical) thread,[1] or it could simply hold onto its argument until get is called and begin evaluation then. But note that in this example, if we want to obtain any degree of parallelism, we require that unit begin evaluating its argument concurrently and return immediately. Can you see why?[2]
1 We’ll use the term logical thread somewhat informally throughout this chapter to mean a computation that runs concurrently with the main execution thread of our program. There need not be a one-to-one correspondence between logical threads and OS threads. We may have a large number of logical threads mapped onto a smaller number of OS threads via thread pooling, for instance.
2 Function arguments in Scala are strictly evaluated from left to right, so if unit delays execution until get is called, we will both spawn the parallel computation and wait for it to finish before spawning the second parallel computation. This means the computation is effectively sequential!
But if unit begins evaluating its argument concurrently, then calling get arguably breaks referential transparency. We can see this by replacing sumL and sumR with their definitions—if we do so, we still get the same result, but our program is no longer parallel:
Par.get(Par.unit(sum(l))) + Par.get(Par.unit(sum(r)))
If unit starts evaluating its argument right away, the next thing to happen is that get will wait for that evaluation to complete. So the two sides of the + sign won’t run in parallel if we simply inline the sumL and sumR variables. We can see that unit has a definite side effect, but only with regard to get. That is, unit simply returns a Par[Int] in this case, representing an asynchronous computation. But as soon as we pass that Par to get, we explicitly wait for it, exposing the side effect. So it seems that we want to avoid calling get, or at least delay calling it until the very end. We want to be able to combine asynchronous computations without waiting for them to finish.
Before we continue, note what we’ve done. First, we conjured up a simple, almost trivial example. We next explored this example a bit to uncover a design choice. Then, via some experimentation, we discovered an interesting consequence of one option and in the process learned something fundamental about the nature of our problem domain! The overall design process is a series of these little adventures. You don’t need any special license to do this sort of exploration, and you don’t need to be an expert in functional programming either. Just dive in and see what you find.
7.1.2. Combining parallel computations
Let’s see if we can avoid the aforementioned pitfall of combining unit and get. If we don’t call get, that implies that our sum function must return a Par[Int]. What consequences does this change reveal? Again, let’s just invent functions with the required signatures:
def sum(ints: IndexedSeq[Int]): Par[Int] =
if (ints.size <= 1)
Par.unit(ints.headOption getOrElse 0)
else {
val (l,r) = ints.splitAt(ints.length/2)
Par.map2(sum(l), sum(r))(_ + _)
}
Exercise 7.1
![]()
Par.map2 is a new higher-order function for combining the result of two parallel computations. What is its signature? Give the most general signature possible (don’t assume it works only for Int).
Observe that we’re no longer calling unit in the recursive case, and it isn’t clear whether unit should accept its argument lazily anymore. In this example, accepting the argument lazily doesn’t seem to provide any benefit, but perhaps this isn’t always the case. Let’s come back to this question later.
What about map2—should it take its arguments lazily? It would make sense for map2 to run both sides of the computation in parallel, giving each side equal opportunity to run (it would seem arbitrary for the order of the map2 arguments to matter—we simply want map2 to indicate that the two computations being combined are independent, and can be run in parallel). What choice lets us implement this meaning? As a simple test case, consider what happens if map2 is strict in both arguments, and we’re evaluating sum(IndexedSeq(1,2,3,4)). Take a minute to work through and understand the following (somewhat stylized) program trace.
Listing 7.3. Program trace for sum
sum(IndexedSeq(1,2,3,4))
map2(
sum(IndexedSeq(1,2)),
sum(IndexedSeq(3,4)))(_ + _)
map2(
map2(
sum(IndexedSeq(1)),
sum(IndexedSeq(2)))(_ + _),
sum(IndexedSeq(3,4)))(_ + _)
map2(
map2(
unit(1),
unit(2))(_ + _),
sum(IndexedSeq(3,4)))(_ + _)
map2(
map2(
unit(1),
unit(2))(_ + _),
map2(
sum(IndexedSeq(3)),
sum(IndexedSeq(4)))(_ + _))(_ + _)
...
In this trace, to evaluate sum(x), we substitute x into the definition of sum, as we’ve done in previous chapters. Because map2 is strict, and Scala evaluates arguments left to right, whenever we encounter map2(sum(x),sum(y))(_ + _), we have to then evaluate sum(x) and so on recursively. This has the rather unfortunate consequence that we’ll strictly construct the entire left half of the tree of summations first before moving on to (strictly) constructing the right half. Here sum(IndexedSeq(1,2)) gets fully expanded before we consider sum(IndexedSeq(3,4)). And if map2 evaluates its arguments in parallel (using whatever resource is being used to implement the parallelism, like a thread pool), that implies the left half of our computation will start executing before we even begin constructing the right half of our computation.
What if we keep map2 strict, but don’t have it begin execution immediately? Does this help? If map2 doesn’t begin evaluation immediately, this implies a Par value is merely constructing a description of what needs to be computed in parallel. Nothing actually occurs until we evaluate this description, perhaps using a get-like function. The problem is that if we construct our descriptions strictly, they’ll be rather heavyweight objects. Looking back at our trace, our description will have to contain the full tree of operations to be performed:
map2(
map2(
unit(1),
unit(2))(_ + _),
map2(
unit(3),
unit(4))(_ + _))(_ + _)
Whatever data structure we use to store this description, it’ll likely occupy more space than the original list itself! It would be nice if our descriptions were more lightweight.
It seems we should make map2 lazy and have it begin immediate execution of both sides in parallel. This also addresses the problem of giving neither side priority over the other.
7.1.3. Explicit forking
Something still doesn’t feel right about our latest choice. Is it always the case that we want to evaluate the two arguments to map2 in parallel? Probably not. Consider this simple hypothetical example:
Par.map2(Par.unit(1), Par.unit(1))(_ + _)
In this case, we happen to know that the two computations we’re combining will execute so quickly that there isn’t much point in spawning off a separate logical thread to evaluate them. But our API doesn’t give us any way of providing this sort of information. That is, our current API is veryinexplicit about when computations get forked off the main thread—the programmer doesn’t get to specify where this forking should occur. What if we make the forking more explicit? We can do that by inventing another function, def fork[A](a: => Par[A]): Par[A], which we can take to mean that the given Par should be run in a separate logical thread:
def sum(ints: IndexedSeq[Int]): Par[Int] =
if (ints.length <= 1)
Par.unit(ints.headOption getOrElse 0)
else {
val (l,r) = ints.splitAt(ints.length/2)
Par.map2(Par.fork(sum(l)), Par.fork(sum(r)))(_ + _)
}
With fork, we can now make map2 strict, leaving it up to the programmer to wrap arguments if they wish. A function like fork solves the problem of instantiating our parallel computations too strictly, but more fundamentally it puts the parallelism explicitly under programmer control. We’re addressing two concerns here. The first is that we need some way to indicate that the results of the two parallel tasks should be combined. Separate from this, we have the choice of whether a particular task should be performed asynchronously. By keeping these concerns separate, we avoid having any sort of global policy for parallelism attached to map2 and other combinators we write, which would mean making tough (and ultimately arbitrary) choices about what global policy is best.
Let’s now return to the question of whether unit should be strict or lazy. With fork, we can now make unit strict without any loss of expressiveness. A non-strict version of it, let’s call it lazyUnit, can be implemented using unit and fork:
def unit[A](a: A): Par[A]
def lazyUnit[A](a: => A): Par[A] = fork(unit(a))
The function lazyUnit is a simple example of a derived combinator, as opposed to a primitive combinator like unit. We were able to define lazyUnit just in terms of other operations. Later, when we pick a representation for Par, lazyUnit won’t need to know anything about this representation—its only knowledge of Par is through the operations fork and unit that are defined on Par.[3]
3 This sort of indifference to representation is a hint that the operations are actually more general, and can be abstracted to work for types other than just Par. We’ll explore this topic in detail in part 3.
We know we want fork to signal that its argument gets evaluated in a separate logical thread. But we still have the question of whether it should begin doing so immediately upon being called, or hold on to its argument, to be evaluated in a logical thread later, when the computation is forcedusing something like get. In other words, should evaluation be the responsibility of fork or of get? Should evaluation be eager or lazy? When you’re unsure about a meaning to assign to some function in your API, you can always continue with the design process—at some point later the trade-offs of different choices of meaning may become clear. Here we make use of a helpful trick—we’ll think about what sort of information is required to implement fork and get with various meanings.
If fork begins evaluating its argument immediately in parallel, the implementation must clearly know something, either directly or indirectly, about how to create threads or submit tasks to some sort of thread pool. Moreover, this implies that the thread pool (or whatever resource we use to implement the parallelism) must be (globally) accessible and properly initialized wherever we want to call fork.[4] This means we lose the ability to control the parallelism strategy used for different parts of our program. And though there’s nothing inherently wrong with having a global resource for executing parallel tasks, we can imagine how it would be useful to have more fine-grained control over what implementations are used where (we might like for each subsystem of a large application to get its own thread pool with different parameters, for example). It seems much more appropriate to give get the responsibility of creating threads and submitting execution tasks.
4 Much like the credit card processing system was accessible to the buyCoffee method in our Cafe example in chapter 1.
Note that coming to these conclusions didn’t require knowing exactly how fork and get will be implemented, or even what the representation of Par will be. We just reasoned informally about the sort of information required to actually spawn a parallel task, and examined the consequences of having Par values know about this information.
In contrast, if fork simply holds on to its unevaluated argument until later, it requires no access to the mechanism for implementing parallelism. It just takes an unevaluated Par and “marks” it for concurrent evaluation. Let’s now assume this meaning for fork. With this model, Par itself doesn’t need to know how to actually implement the parallelism. It’s more a description of a parallel computation that gets interpreted at a later time by something like the get function. This is a shift from before, where we were considering Par to be a container of a value that we could simply get when it becomes available. Now it’s more of a first-class program that we can run. So let’s rename our get function to run, and dictate that this is where the parallelism actually gets implemented:
def run[A](a: Par[A]): A
Because Par is now just a pure data structure, run has to have some means of implementing the parallelism, whether it spawns new threads, delegates tasks to a thread pool, or uses some other mechanism.
7.2. Picking a representation
Just by exploring this simple example and thinking through the consequences of different choices, we’ve sketched out the following API.
Listing 7.4. Basic sketch for an API for Par

We’ve also loosely assigned meaning to these various functions:
· unit promotes a constant value to a parallel computation.
· map2 combines the results of two parallel computations with a binary function.
· fork marks a computation for concurrent evaluation. The evaluation won’t actually occur until forced by run.
· lazyUnit wraps its unevaluated argument in a Par and marks it for concurrent evaluation.
· run extracts a value from a Par by actually performing the computation.
At any point while sketching out an API, you can start thinking about possible representations for the abstract types that appear.
Exercise 7.2
![]()
Before continuing, try to come up with representations for Par that make it possible to implement the functions of our API.
Let’s see if we can come up with a representation. We know run needs to execute asynchronous tasks somehow. We could write our own low-level API, but there’s already a class that we can use in the Java Standard Library, java.util.concurrent .ExecutorService. Here is its API, excerpted and transcribed to Scala:

So ExecutorService lets us submit a Callable value (in Scala we’d probably just use a lazy argument to submit) and get back a corresponding Future that’s a handle to a computation that’s potentially running in a separate thread. We can obtain a value from a Future with its getmethod (which blocks the current thread until the value is available), and it has some extra features for cancellation (throwing an exception after blocking for a certain amount of time, and so on).
Let’s try assuming that our run function has access to an ExecutorService and see if that suggests anything about the representation for Par:
def run[A](s: ExecutorService)(a: Par[A]): A
The simplest possible model for Par[A] might be ExecutorService => A. This would obviously make run trivial to implement. But it might be nice to defer the decision of how long to wait for a computation, or whether to cancel it, to the caller of run. So Par[A] becomesExecutorService => Future[A], and run simply returns the Future:
type Par[A] = ExecutorService => Future[A]
def run[A](s: ExecutorService)(a: Par[A]): Future[A] = a(s)
Note that since Par is represented by a function that needs an ExecutorService, the creation of the Future doesn’t actually happen until this ExectorService is provided.
Is it really that simple? Let’s assume it is for now, and revise our model if we find it doesn’t allow some functionality we’d like.
7.3. Refining the API
The way we’ve worked so far is a bit artificial. In practice, there aren’t such clear boundaries between designing the API and choosing a representation, and one doesn’t necessarily precede the other. Ideas for a representation can inform the API, the API can inform the choice of representation, and it’s natural to shift fluidly between these two perspectives, run experiments as questions arise, build prototypes, and so on.
We’ll devote this section to exploring our API. Though we got a lot of mileage out of considering a simple example, before we add any new primitive operations, let’s try to learn more about what’s expressible using those we already have. With our primitives and choices of meaning for them, we’ve carved out a little universe for ourselves. We now get to discover what ideas are expressible in this universe. This can and should be a fluid process—we can change the rules of our universe at any time, make a fundamental change to our representation or introduce a new primitive, and explore how our creation then behaves.
Let’s begin by implementing the functions of the API that we’ve developed so far. Now that we have a representation for Par, a first crack at it should be straightforward. What follows is a simplistic implementation using the representation of Par that we’ve chosen.
Listing 7.5. Basic implementation for Par
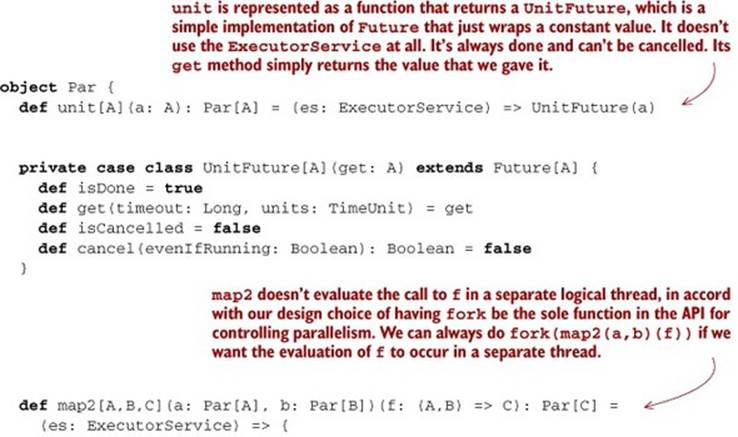

We should note that Future doesn’t have a purely functional interface. This is part of the reason why we don’t want users of our library to deal with Future directly. But importantly, even though methods on Future rely on side effects, our entire Par API remains pure. It’s only after the user calls run and the implementation receives an ExecutorService that we expose the Future machinery. Our users therefore program to a pure interface whose implementation nevertheless relies on effects at the end of the day. But since our API remains pure, these effects aren’t sideeffects. In part 4 we’ll discuss this distinction in detail.
Exercise 7.3
![]()
Hard: Fix the implementation of map2 so that it respects the contract of timeouts on Future.
Exercise 7.4
![]()
This API already enables a rich set of operations. Here’s a simple example: using lazyUnit, write a function to convert any function A => B to one that evaluates its result asynchronously.
def asyncF[A,B](f: A => B): A => Par[B]
Adding infix syntax using implicit conversions
If Par were an actual data type, functions like map2 could be placed in the class body and then called with infix syntax like x.map2(y)(f) (much like we did for Stream and Option). But since Par is just a type alias, we can’t do this directly. There’s a trick to add infix syntax to any type using implicit conversions. We won’t discuss that here since it isn’t that relevant to what we’re trying to cover, but if you’re interested, check out the answer code associated with this chapter.
What else can we express with our existing combinators? Let’s look at a more concrete example.
Suppose we have a Par[List[Int]] representing a parallel computation that produces a List[Int], and we’d like to convert this to a Par[List[Int]] whose result is sorted:
def sortPar(parList: Par[List[Int]]): Par[List[Int]]
We could of course run the Par, sort the resulting list, and repackage it in a Par with unit. But we want to avoid calling run. The only other combinator we have that allows us to manipulate the value of a Par in any way is map2. So if we passed parList to one side of map2, we’d be able to gain access to the List inside and sort it. And we can pass whatever we want to the other side of map2, so let’s just pass a no-op:
def sortPar(parList: Par[List[Int]]): Par[List[Int]] =
map2(parList, unit(()))((a, _) => a.sorted)
That was easy. We can now tell a Par[List[Int]] that we’d like that list sorted. But we might as well generalize this further. We can “lift” any function of type A => B to become a function that takes Par[A] and returns Par[B]; we can map any function over a Par:
def map[A,B](pa: Par[A])(f: A => B): Par[B] =
map2(pa, unit(()))((a,_) => f(a))
For instance, sortPar is now simply this:
def sortPar(parList: Par[List[Int]]) = map(parList)(_.sorted)
That’s terse and clear. We just combined the operations to make the types line up. And yet, if you look at the implementations of map2 and unit, it should be clear this implementation of map means something sensible.
Was it cheating to pass a bogus value, unit(()), as an argument to map2, only to ignore its value? Not at all! The fact that we can implement map in terms of map2, but not the other way around, just shows that map2 is strictly more powerful than map. This sort of thing happens a lot when we’re designing libraries—often, a function that seems to be primitive will turn out to be expressible using some more powerful primitive.
What else can we implement using our API? Could we map over a list in parallel? Unlike map2, which combines two parallel computations, parMap (let’s call it) needs to combine N parallel computations. It seems like this should somehow be expressible:
def parMap[A,B](ps: List[A])(f: A => B): Par[List[B]]
We could always just write parMap as a new primitive. Remember that Par[A] is simply an alias for ExecutorService => Future[A].
There’s nothing wrong with implementing operations as new primitives. In some cases, we can even implement the operations more efficiently by assuming something about the underlying representation of the data types we’re working with. But right now we’re interested in exploring what operations are expressible using our existing API, and grasping the relationships between the various operations we’ve defined. Understanding what combinators are truly primitive will become more important in part 3, when we show how to abstract over common patterns across libraries.[5]
5 In this case, there’s another good reason not to implement parMap as a new primitive—it’s challenging to do correctly, particularly if we want to properly respect timeouts. It’s frequently the case that primitive combinators encapsulate some rather tricky logic, and reusing them means we don’t have to duplicate this logic.
Let’s see how far we can get implementing parMap in terms of existing combinators:
def parMap[A,B](ps: List[A])(f: A => B): Par[List[B]] = {
val fbs: List[Par[B]] = ps.map(asyncF(f))
...
}
Remember, asyncF converts an A => B to an A => Par[B] by forking a parallel computation to produce the result. So we can fork off our N parallel computations pretty easily, but we need some way of collecting their results. Are we stuck? Well, just from inspecting the types, we can see that we need some way of converting our List[Par[B]] to the Par[List[B]] required by the return type of parMap.
Exercise 7.5
![]()
Hard: Write this function, called sequence. No additional primitives are required. Do not call run.
def sequence[A](ps: List[Par[A]]): Par[List[A]]
Once we have sequence, we can complete our implementation of parMap:
def parMap[A,B](ps: List[A])(f: A => B): Par[List[B]] = fork {
val fbs: List[Par[B]] = ps.map(asyncF(f))
sequence(fbs)
}
Note that we’ve wrapped our implementation in a call to fork. With this implementation, parMap will return immediately, even for a huge input list. When we later call run, it will fork a single asynchronous computation which itself spawns N parallel computations, and then waits for these computations to finish, collecting their results into a list.
Exercise 7.6
![]()
Implement parFilter, which filters elements of a list in parallel.
def parFilter[A](as: List[A])(f: A => Boolean): Par[List[A]]
Can you think of any other useful functions to write? Experiment with writing a few parallel computations of your own to see which ones can be expressed without additional primitives. Here are some ideas to try:
· Is there a more general version of the parallel summation function we wrote at the beginning of this chapter? Try using it to find the maximum value of an IndexedSeq in parallel.
· Write a function that takes a list of paragraphs (a List[String]) and returns the total number of words across all paragraphs, in parallel. Generalize this function as much as possible.
· Implement map3, map4, and map5, in terms of map2.
7.4. The algebra of an API
As the previous section demonstrates, we often get far just by writing down the type signature for an operation we want, and then “following the types” to an implementation. When working this way, we can almost forget the concrete domain (for instance, when we implemented map in terms of map2 and unit) and just focus on lining up types. This isn’t cheating; it’s a natural style of reasoning, analogous to the reasoning one does when simplifying an algebraic equation. We’re treating the API as an algebra,[6] or an abstract set of operations along with a set of laws or properties we assume to be true, and simply doing formal symbol manipulation following the rules of the game specified by this algebra.
6 We do mean algebra in the mathematical sense of one or more sets, together with a collection of functions operating on objects of these sets, and a set of axioms. Axioms are statements assumed true from which we can derive other theorems that must also be true. In our case, the sets are particular types like Par[A] and List[Par[A]], and the functions are operations like map2, unit, and sequence.
Up until now, we’ve been reasoning somewhat informally about our API. There’s nothing wrong with this, but it can be helpful to take a step back and formalize what laws you expect to hold (or would like to hold) for your API.[7] Without realizing it, you’ve probably mentally built up a model of what properties or laws you expect. Actually writing these down and making them precise can highlight design choices that wouldn’t be otherwise apparent when reasoning informally.
7 We’ll have much more to say about this throughout the rest of this book. In the next chapter, we’ll design a declarative testing library that lets us define properties we expect functions to satisfy, and automatically generates test cases to check these properties. And in part 3 we’ll introduce abstract interfaces specified only by sets of laws.
7.4.1. The law of mapping
Like any design choice, choosing laws has consequences—it places constraints on what the operations can mean, determines what implementation choices are possible, and affects what other properties can be true. Let’s look at an example. We’ll just make up a possible law that seems reasonable. This might be used as a test case if we were writing tests for our library:
map(unit(1))(_ + 1) == unit(2)
We’re saying that mapping over unit(1) with the _ + 1 function is in some sense equivalent to unit(2). (Laws often start out this way, as concrete examples of identities[8] we expect to hold.) In what sense are they equivalent? This is an interesting question. For now, let’s say two Parobjects are equivalent if for any valid ExecutorService argument, their Future results have the same value.
8 Here we mean identity in the mathematical sense of a statement that two expressions are identical or equivalent.
We can check that this holds for a particular ExecutorService with a function like this:
def equal[A](e: ExecutorService)(p: Par[A], p2: Par[A]): Boolean =
p(e).get == p2(e).get
Laws and functions share much in common. Just as we can generalize functions, we can generalize laws. For instance, the preceding could be generalized this way:
map(unit(x))(f) == unit(f(x))
Here we’re saying this should hold for any choice of x and f, not just 1 and the _ + 1 function. This places some constraints on our implementation. Our implementation of unit can’t, say, inspect the value it receives and decide to return a parallel computation with a result of 42 when the input is 1—it can only pass along whatever it receives. Similarly for our ExecutorService—when we submit Callable objects to it for execution, it can’t make any assumptions or change behavior based on the values it receives. More concretely, this law disallows downcasting orisInstanceOf checks (often grouped under the term typecasing) in the implementations of map and unit.
Much like we strive to define functions in terms of simpler functions, each of which do just one thing, we can define laws in terms of simpler laws that each say just one thing. Let’s see if we can simplify this law further. We said we wanted this law to hold for any choice of x and f. Something interesting happens if we substitute the identity function for f.[9] We can simplify both sides of the equation and get a new law that’s considerably simpler:[10]
9 The identity function is defined as def id[A](a: A): A = a.
10 This is the same sort of substitution and simplification one might do when solving an algebraic equation.

Fascinating! Our new, simpler law talks only about map—apparently the mention of unit was an extraneous detail. To get some insight into what this new law is saying, let’s think about what map can’t do. It can’t, say, throw an exception and crash the computation before applying the function to the result (can you see why this violates the law?). All it can do is apply the function f to the result of y, which of course leaves y unaffected when that function is id.[11] Even more interestingly, given map(y)(id) == y, we can perform the substitutions in the other direction to get back our original, more complex law. (Try it!) Logically, we have the freedom to do so because map can’t possibly behave differently for different function types it receives. Thus, given map(y)(id) == y, it must be true that map(unit(x))(f) == unit(f(x)). Since we get this second law or theorem for free, simply because of the parametricity of map, it’s sometimes called a free theorem.[12]
11 We say that map is required to be structure-preserving in that it doesn’t alter the structure of the parallel computation, only the value “inside” the computation.
12 The idea of free theorems was introduced by Philip Wadler in the classic paper “Theorems for Free!” (http://mng.bz/Z9f1).
Exercise 7.7
![]()
Hard: Given map(y)(id) == y, it’s a free theorem that map(map(y)(g))(f) == map(y)(f compose g). (This is sometimes called map fusion, and it can be used as an optimization—rather than spawning a separate parallel computation to compute the second mapping, we can fold it into the first mapping.)[13] Can you prove it? You may want to read the paper “Theorems for Free!” (http://mng.bz/Z9f1) to better understand the “trick” of free theorems.
13 Our representation of Par doesn’t give us the ability to implement this optimization, since it’s an opaque function. If it were reified as a data type, we could pattern match and discover opportunities to apply this rule. You may want to try experimenting with this idea on your own.
7.4.2. The law of forking
As interesting as all this is, this particular law doesn’t do much to constrain our implementation. You’ve probably been assuming these properties without even realizing it (it would be strange to have any special cases in the implementations of map, unit, or ExecutorService.submit, or have map randomly throwing exceptions). Let’s consider a stronger property—that fork should not affect the result of a parallel computation:
fork(x) == x
This seems like it should be obviously true of our implementation, and it is clearly a desirable property, consistent with our expectation of how fork should work. fork(x) should do the same thing as x, but asynchronously, in a logical thread separate from the main thread. If this law didn’t always hold, we’d have to somehow know when it was safe to call without changing meaning, without any help from the type system.
Surprisingly, this simple property places strong constraints on our implementation of fork. After you’ve written down a law like this, take off your implementer hat, put on your debugger hat, and try to break your law. Think through any possible corner cases, try to come up with counterexamples, and even construct an informal proof that the law holds—at least enough to convince a skeptical fellow programmer.
7.4.3. Breaking the law: a subtle bug
Let’s try this mode of thinking. We’re expecting that fork(x) == x for all choices of x, and any choice of ExecutorService. We have a good sense of what x could be—it’s some expression making use of fork, unit, and map2 (and other combinators derived from these). What aboutExecutorService? What are some possible implementations of it? There’s a good listing of different implementations in the class java.util .concurrent.Executors (API link: http://mng.bz/urQd).
Exercise 7.8
![]()
Hard: Take a look through the various static methods in Executors to get a feel for the different implementations of ExecutorService that exist. Then, before continuing, go back and revisit your implementation of fork and try to find a counterexample or convince yourself that the law holds for your implementation.
Why laws about code and proofs are important
It may seem unusual to state and prove properties about an API. This certainly isn’t something typically done in ordinary programming. Why is it important in FP?
In functional programming it’s easy, and expected, to factor out common functionality into generic, reusable components that can be composed. Side effects hurt compositionality, but more generally, any hidden or out-of-band assumption or behavior that prevents us from treating our components (be they functions or anything else) as black boxes makes composition difficult or impossible.
In our example of the law for fork, we can see that if the law we posited didn’t hold, many of our general-purpose combinators, like parMap, would no longer be sound (and their usage might be dangerous, since they could, depending on the broader parallel computation they were used in, result in deadlocks).
Giving our APIs an algebra, with laws that are meaningful and aid reasoning, makes the APIs more usable for clients, but also means we can treat the objects of our APIs as black boxes. As we’ll see in part 3, this is crucial for our ability to factor out common patterns across the different libraries we’ve written.
There’s actually a rather subtle problem that will occur in most implementations of fork. When using an ExecutorService backed by a thread pool of bounded size (see Executors.newFixedThreadPool), it’s very easy to run into a deadlock.[14] Suppose we have anExecutorService backed by a thread pool where the maximum number of threads is 1. Try running the following example using our current implementation:
14 In the next chapter, we’ll write a combinator library for testing that can help discover problems like these automatically.
val a = lazyUnit(42 + 1)
val S = Executors.newFixedThreadPool(1)
println(Par.equal(S)(a, fork(a)))
Most implementations of fork will result in this code deadlocking. Can you see why? Let’s look again at our implementation of fork:

Note that we’re submitting the Callable first, and within that Callable, we’re submitting another Callable to the ExecutorService and blocking on its result (recall that a(es) will submit a Callable to the ExecutorService and get back a Future). This is a problem if our thread pool has size 1. The outer Callable gets submitted and picked up by the sole thread. Within that thread, before it will complete, we submit and block waiting for the result of another Callable. But there are no threads available to run this Callable. They’re waiting on each other and therefore our code deadlocks.
Exercise 7.9
![]()
Hard: Show that any fixed-size thread pool can be made to deadlock given this implementation of fork.
When you find counterexamples like this, you have two choices—you can try to fix your implementation such that the law holds, or you can refine your law a bit, to state more explicitly the conditions under which it holds (you could simply stipulate that you require thread pools that can grow unbounded). Even this is a good exercise—it forces you to document invariants or assumptions that were previously implicit.
Can we fix fork to work on fixed-size thread pools? Let’s look at a different implementation:
def fork[A](fa: => Par[A]): Par[A] =
es => fa(es)
This certainly avoids deadlock. The only problem is that we aren’t actually forking a separate logical thread to evaluate fa. So fork(hugeComputation)(es) for some ExecutorService es, would run hugeComputation in the main thread, which is exactly what we wanted to avoid by calling fork. This is still a useful combinator, though, since it lets us delay instantiation of a computation until it’s actually needed. Let’s give it a name, delay:
def delay[A](fa: => Par[A]): Par[A] =
es => fa(es)
But we’d really like to be able to run arbitrary computations over fixed-size thread pools. In order to do that, we’ll need to pick a different representation of Par.
7.4.4. A fully non-blocking Par implementation using actors
In this section, we’ll develop a fully non-blocking implementation of Par that works for fixed-size thread pools. Since this isn’t essential to our overall goals of discussing various aspects of functional design, you may skip to the next section if you prefer. Otherwise, read on.
The essential problem with the current representation is that we can’t get a value out of a Future without the current thread blocking on its get method. A representation of Par that doesn’t leak resources this way has to be non-blocking in the sense that the implementations of fork andmap2 must never call a method that blocks the current thread like Future.get. Writing such an implementation correctly can be challenging. Fortunately we have our laws with which to test our implementation, and we only have to get it right once. After that, the users of our library can enjoy a composable and abstract API that does the right thing every time.
In the code that follows, you don’t need to understand exactly what’s going on with every part of it. We just want to show you, using real code, what a correct representation of Par that respects the laws might look like.
The Basic Idea
How can we implement a non-blocking representation of Par? The idea is simple. Instead of turning a Par into a java.util.concurrent.Future that we can get a value out of (which requires blocking), we’ll introduce our own version of Future with which we can register a callback that will be invoked when the result is ready. This is a slight shift in perspective:

Our Par type looks identical, except we’re now using our new version of Future, which has a different API than the one in java.util.concurrent. Rather than calling get to obtain the result from our Future, our Future instead has an apply method that receives a function k that expects the result of type A and uses it to perform some effect. This kind of function is sometimes called a continuation or a callback.
The apply method is marked private[parallelism] so that we don’t expose it to users of our library. Marking it private[parallelism] ensures that it can only be accessed from code within the fpinscala.parallelism package. This is so that our API remains pure and we can guarantee that our laws hold.
Using local side effects for a pure API
The Future type we defined here is rather imperative. An A => Unit? Such a function can only be useful for executing some side effect using the given A, as we certainly aren’t using the returned result. Are we still doing functional programming in using a type like Future? Yes, but we’re making use of a common technique of using side effects as an implementation detail for a purely functional API. We can get away with this because the side effects we use are not observable to code that uses Par. Note that Future.apply is protected and can’t even be called by outside code.
As we go through the rest of our implementation of the non-blocking Par, you may want to convince yourself that the side effects employed can’t be observed by outside code. The notion of local effects, observability, and subtleties of our definitions of purity and referential transparency are discussed in much more detail in chapter 14, but for now an informal understanding is fine.
With this representation of Par, let’s look at how we might implement the run function first, which we’ll change to just return an A. Since it goes from Par[A] to A, it will have to construct a continuation and pass it to the Future value’s apply method.
Listing 7.6. Implementing run for Par

It should be noted that run blocks the calling thread while waiting for the latch. It’s not possible to write an implementation of run that doesn’t block. Since it needs to return a value of type A, it has to wait for that value to become available before it can return. For this reason, we want users of our API to avoid calling run until they definitely want to wait for a result. We could even go so far as to remove run from our API altogether and expose the apply method on Par instead so that users can register asynchronous callbacks. That would certainly be a valid design choice, but we’ll leave our API as it is for now.
Let’s look at an example of actually creating a Par. The simplest one is unit:

Since unit already has a value of type A available, all it needs to do is call the continuation cb, passing it this value. If that continuation is the one from our run implementation, for example, this will release the latch and make the result available immediately.
What about fork? This is where we introduce the actual parallelism:

When the Future returned by fork receives its continuation cb, it will fork off a task to evaluate the by-name argument a. Once the argument has been evaluated and called to produce a Future[A], we register cb to be invoked when that Future has its resulting A.
What about map2? Recall the signature:
def map2[A,B,C](a: Par[A], b: Par[B])(f: (A,B) => C): Par[C]
Here, a non-blocking implementation is considerably trickier. Conceptually, we’d like map2 to run both Par arguments in parallel. When both results have arrived, we want to invoke f and then pass the resulting C to the continuation. But there are several race conditions to worry about here, and a correct non-blocking implementation is difficult using only the low-level primitives of java.util.concurrent.
A Brief Introduction to Actors
To implement map2, we’ll use a non-blocking concurrency primitive called actors. An Actor is essentially a concurrent process that doesn’t constantly occupy a thread. Instead, it only occupies a thread when it receives a message. Importantly, although multiple threads may be concurrently sending messages to an actor, the actor processes only one message at a time, queueing other messages for subsequent processing. This makes them useful as a concurrency primitive when writing tricky code that must be accessed by multiple threads, and which would otherwise be prone to race conditions or deadlocks.
It’s best to illustrate this with an example. Many implementations of actors would suit our purposes just fine, including one in the Scala standard library (see scala.actors.Actor), but in the interest of simplicity we’ll use our own minimal actor implementation included with the chapter code in the file Actor.scala:

Let’s try out this Actor:

It’s not at all essential to understand the Actor implementation. A correct, efficient implementation is rather subtle, but if you’re curious, see the Actor.scala file in the chapter code. The implementation is just under 100 lines of ordinary Scala code.[15]
15 The main trickiness in an actor implementation has to do with the fact that multiple threads may be messaging the actor simultaneously. The implementation needs to ensure that messages are processed only one at a time, and also that all messages sent to the actor will be processed eventually rather than queued indefinitely. Even so, the code ends up being short.
Implementing Map2 via Actors
We can now implement map2 using an Actor to collect the result from both arguments. The code is straightforward, and there are no race conditions to worry about, since we know that the Actor will only process one message at a time.
Listing 7.7. Implementing map2 with Actor

Given these implementations, we should now be able to run Par values of arbitrary complexity without having to worry about running out of threads, even if the actors only have access to a single JVM thread.
Let’s try this out in the REPL:
scala> import java.util.concurrent.Executors
scala> val p = parMap(List.range(1, 100000))(math.sqrt(_))
p: ExecutorService => Future[List[Double]] = < function >
scala> val x = run(Executors.newFixedThreadPool(2))(p)
x: List[Double] = List(1.0, 1.4142135623730951, 1.7320508075688772,
2.0, 2.23606797749979, 2.449489742783178, 2.6457513110645907, 2.828
4271247461903, 3.0, 3.1622776601683795, 3.3166247903554, 3.46410...
That will call fork about 100,000 times, starting that many actors to combine these values two at a time. Thanks to our non-blocking Actor implementation, we don’t need 100,000 JVM threads to do that in.
Fantastic. Our law of forking now holds for fixed-size thread pools.
Exercise 7.10
![]()
Hard: Our non-blocking representation doesn’t currently handle errors at all. If at any point our computation throws an exception, the run implementation’s latch never counts down and the exception is simply swallowed. Can you fix that?
Taking a step back, the purpose of this section hasn’t necessarily been to figure out the best non-blocking implementation of fork, but more to show that laws are important. They give us another angle to consider when thinking about the design of a library. If we hadn’t tried writing out some of the laws of our API, we may not have discovered the thread resource leak in our first implementation until much later.
In general, there are multiple approaches you can consider when choosing laws for your API. You can think about your conceptual model, and reason from there to postulate laws that should hold. You can also just invent laws you think might be useful or instructive (like we did with ourfork law), and see if it’s possible and sensible to ensure that they hold for your model. And lastly, you can look at your implementation and come up with laws you expect to hold based on that.[16]
16 This last way of generating laws is probably the weakest, since it can be too easy to just have the laws reflect the implementation, even if the implementation is buggy or requires all sorts of unusual side conditions that make composition difficult.
7.5. Refining combinators to their most general form
Functional design is an iterative process. After you write down your API and have at least a prototype implementation, try using it for progressively more complex or realistic scenarios. Sometimes you’ll find that these scenarios require new combinators. But before jumping right to implementation, it’s a good idea to see if you can refine the combinator you need to its most general form. It may be that what you need is just a specific case of some more general combinator.
About the exercises in this section
The exercises and answers in this section use our original simpler (blocking) representation of Par[A]. If you’d like to work through the exercises and answers using the non-blocking implementation we developed in the previous section instead, see the file Nonblocking.scala in both theexercises and answers projects.
Let’s look at an example of this. Suppose we want a function to choose between two forking computations based on the result of an initial computation:
def choice[A](cond: Par[Boolean])(t: Par[A], f: Par[A]): Par[A]
This constructs a computation that proceeds with t if cond results in true, or f if cond results in false. We can certainly implement this by blocking on the result of the cond, and then using this result to determine whether to run t or f. Here’s a simple blocking implementation:[17]
17 See Nonblocking.scala in the chapter code for the non-blocking implementation.

But before we call ourselves good and move on, let’s think about this combinator a bit. What is it doing? It’s running cond and then, when the result is available, it runs either t or f. This seems reasonable, but let’s see if we can think of some variations to get at the essence of this combinator. There’s something rather arbitrary about the use of Boolean here, and the fact that we’re only selecting among two possible parallel computations, t and f. Why just two? If it’s useful to be able to choose between two parallel computations based on the results of a first, it should be certainly be useful to choose between N computations:
def choiceN[A](n: Par[Int])(choices: List[Par[A]]): Par[A]
Let’s say that choiceN runs n, and then uses that to select a parallel computation from choices. This is a bit more general than choice.
Exercise 7.11
![]()
Implement choiceN and then choice in terms of choiceN.
Note what we’ve done so far. We’ve refined our original combinator, choice, to choiceN, which turns out to be more general, capable of expressing choice as well as other use cases not supported by choice. But let’s keep going to see if we can refine choice to an even more general combinator.
Exercise 7.12
![]()
There’s still something rather arbitrary about choiceN. The choice of List seems overly specific. Why does it matter what sort of container we have? For instance, what if, instead of a list of computations, we have a Map of them:[18]
18 Map[K,V] (API link: http://mng.bz/eZ4l) is a purely functional data structure in the Scala standard library. It associates keys of type K with values of type V in a one-to-one relationship, and allows us to look up the value by the associated key.
def choiceMap[K,V](key: Par[K])(choices: Map[K,Par[V]]): Par[V]
If you want, stop reading here and see if you can come up with a new and more general combinator in terms of which you can implement choice, choiceN, and choiceMap.
The Map encoding of the set of possible choices feels overly specific, just like List. If we look at our implementation of choiceMap, we can see we aren’t really using much of the API of Map. Really, the Map[A,Par[B]] is used to provide a function, A => Par[B]. And now that we’ve spotted that, looking back at choice and choiceN, we can see that for choice, the pair of arguments was just being used as a function of type Boolean => Par[A] (where the Boolean selects one of the two Par[A] arguments), and for choiceN the list was just being used as a function of type Int => Par[A]!
Let’s make a more general signature that unifies them all:
def chooser[A,B](pa: Par[A])(choices: A => Par[B]): Par[B]
Exercise 7.13
![]()
Implement this new primitive chooser, and then use it to implement choice and choiceN.
Whenever you generalize functions like this, take a critical look at your generalized function when you’re finished. Although the function may have been motivated by some specific use case, the signature and implementation may have a more general meaning. In this case, chooser is perhaps no longer the most appropriate name for this operation, which is actually quite general—it’s a parallel computation that, when run, will run an initial computation whose result is used to determine a second computation. Nothing says that this second computation needs to even exist before the first computation’s result is available. It doesn’t need to be stored in a container like List or Map. Perhaps it’s being generated from whole cloth using the result of the first computation. This function, which comes up often in functional libraries, is usually called bind orflatMap:
def flatMap[A,B](a: Par[A])(f: A => Par[B]): Par[B]
Is flatMap really the most primitive possible function, or can we generalize further? Let’s play around with it a bit more. The name flatMap is suggestive of the fact that this operation could be decomposed into two steps: mapping f: A => Par[B] over our Par[A], which generates aPar[Par[B]], and then flattening this nested Par[Par[B]] to a Par[B]. But this is interesting—it suggests that all we needed to do was add an even simpler combinator, let’s call it join, for converting a Par[Par[X]] to Par[X] for any choice of X:
def join[A](a: Par[Par[A]]): Par[A]
Again we’re just following the types. We have an example that demands a function with the given signature, and so we just bring it into existence. Now that it exists, we can think about what the signature means. We call it join since conceptually it’s a parallel computation that, when run, will execute the inner computation, wait for it to finish (much like Thread.join), and then return its result.
Exercise 7.14
![]()
Implement join. Can you see how to implement flatMap using join? And can you implement join using flatMap?
We’ll stop here, but you’re encouraged to explore this algebra further. Try more complicated examples, discover new combinators, and see what you find! Here are some questions to consider:
· Can you implement a function with the same signature as map2, but using flatMap and unit? How is its meaning different than that of map2?
· Can you think of laws relating join to the other primitives of the algebra?
· Are there parallel computations that can’t be expressed using this algebra? Can you think of any computations that can’t even be expressed by adding new primitives to the algebra?
Recognizing the expressiveness and limitations of an algebra
As you practice more functional programming, one of the skills you’ll develop is the ability to recognize what functions are expressible from an algebra, and what the limitations of that algebra are. For instance, in the preceding example, it may not have been obvious at first that a function like choice couldn’t be expressed purely in terms of map, map2, and unit, and it may not have been obvious that choice was just a special case of flatMap. Over time, observations like this will come quickly, and you’ll also get better at spotting how to modify your algebra to make some needed combinator expressible. These skills will be helpful for all of your API design work.
As a practical consideration, being able to reduce an API to a minimal set of primitive functions is extremely useful. As we noted earlier when we implemented parMap in terms of existing combinators, it’s frequently the case that primitive combinators encapsulate some rather tricky logic, and reusing them means we don’t have to duplicate this logic.
7.6. Summary
We’ve now completed the design of a library for defining parallel and asynchronous computations in a purely functional way. Although this domain is interesting, the primary goal of this chapter was to give you a window into the process of functional design, a sense of the sorts of issues you’re likely to encounter, and ideas for how you can handle those issues.
Chapters 4 through 6 had a strong theme of separation of concerns: specifically, the idea of separating the description of a computation from the interpreter that then runs it. In this chapter, we saw that principle in action in the design of a library that describes parallel computations as values of a data type Par, with a separate interpreter run to actually spawn the threads to execute them.
In the next chapter, we’ll look at a completely different domain, take another meandering journey toward an API for that domain, and draw further lessons about functional design.