Functional Programming in Scala (2015)
Part 2. Functional design and combinator libraries
Chapter 8. Property-based testing
In chapter 7 we worked through the design of a functional library for expressing parallel computations. There we introduced the idea that an API should form an algebra—that is, a collection of data types, functions over these data types, and importantly, laws or properties that express relationships between these functions. We also hinted at the idea that it might be possible to somehow check these laws automatically.
This chapter will take us toward a simple but powerful library for property-based testing. The general idea of such a library is to decouple the specification of program behavior from the creation of test cases. The programmer focuses on specifying the behavior of programs and giving high-level constraints on the test cases; the framework then automatically generates test cases that satisfy these constraints, and runs tests to ensure that programs behave as specified.
Although a library for testing has a very different purpose than a library for parallel computations, we’ll discover that these libraries have a lot of surprisingly similar combinators. This similarity is something we’ll return to in part 3.
8.1. A brief tour of property-based testing
As an example, in ScalaCheck (http://mng.bz/n2j9), a property-based testing library for Scala, a property looks something like this.
Listing 8.1. ScalaCheck properties

And we can check properties like so:
scala> prop.check
+ OK, passed 100 tests.
scala> failingProp.check
! Falsified after 6 passed tests.
> ARG_0: List(0, 1)
Here, intList is not a List[Int], but a Gen[List[Int]], which is something that knows how to generate test data of type List[Int]. We can sample from this generator, and it will produce lists of different lengths, filled with random numbers between 0 and 100. Generators in a property-based testing library have a rich API. We can combine and compose generators in different ways, reuse them, and so on.
The function forAll creates a property by combining a generator of type Gen[A] with some predicate of type A => Boolean. The property asserts that all values produced by the generator should satisfy the predicate. Like generators, properties can also have a rich API. In this simple example we’ve used && to combine two properties. The resulting property will hold only if neither property can be falsified by any of the generated test cases. Together, the two properties form a partial specification of the correct behavior of the reverse method.[1]
1 The goal of this sort of testing is not necessarily to fully specify program behavior, but to give greater confidence in the code. Like testing in general, we can always make our properties more complete, but we should do the usual cost-benefit analysis to determine if the additional work is worth doing.
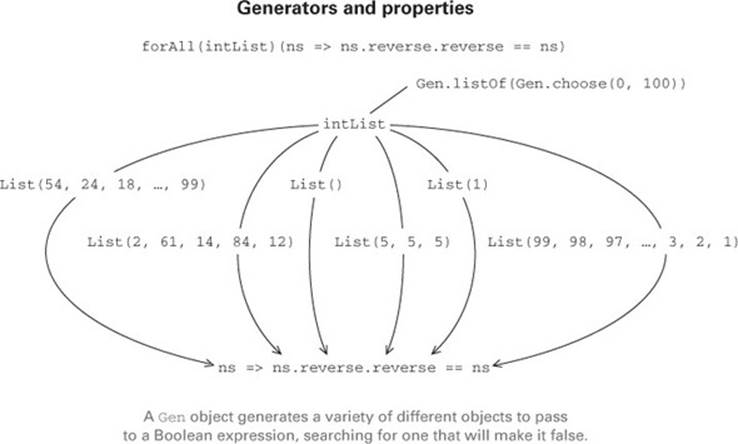
When we invoke prop.check, ScalaCheck will randomly generate List[Int] values to try to find a case that falsifies the predicates that we’ve supplied. The output indicates that ScalaCheck has generated 100 test cases (of type List[Int]) and that they all satisfied the predicates. Properties can of course fail—the output of failingProp.check indicates that the predicate tested false for some input, which is helpfully printed out to facilitate further testing or debugging.
Exercise 8.1
![]()
To get used to thinking about testing in this way, come up with properties that specify the implementation of a sum: List[Int] => Int function. You don’t have to write your properties down as executable ScalaCheck code—an informal description is fine. Here are some ideas to get you started:
· Reversing a list and summing it should give the same result as summing the original, nonreversed list.
· What should the sum be if all elements of the list are the same value?
· Can you think of other properties?
Exercise 8.2
![]()
What properties specify a function that finds the maximum of a List[Int]?
Property-based testing libraries often come equipped with other useful features. We’ll talk more about some of these features later, but just to give an idea of what’s possible:
· Test case minimization —In the event of a failing test, the framework tries smaller sizes until it finds the smallest test case that also fails, which is more illuminating for debugging purposes. For instance, if a property fails for a list of size 10, the framework tries smaller lists and reports the smallest list that fails the test.
· Exhaustive test case generation —We call the set of values that could be produced by some Gen[A] the domain.[2] When the domain is small enough (for instance, if it’s all even integers less than 100), we may exhaustively test all its values, rather than generate sample values. If the property holds for all values in a domain, we have an actual proof, rather than just the absence of evidence to the contrary.
2 This is the same usage of “domain” as the domain of a function (http://mng.bz/ZP8q)—generators describe possible inputs to functions we’d like to test. Note that we’ll also still sometimes use “domain” in the more colloquial sense, to refer to a subject or area of interest, for example, “the domain of functional parallelism” or “the error-handling domain.”
ScalaCheck is just one property-based testing library. And while there’s nothing wrong with it, we’ll derive our own library in this chapter, starting from scratch. Like in chapter 7, this is mostly for pedagogical purposes, but also partly because we should consider no library to be the final word on any subject. There’s certainly nothing wrong with using an existing library like ScalaCheck, and existing libraries can be a good source of ideas. But even if you decide you like the existing library’s solution, spending an hour or two playing with designs and writing down some type signatures is a great way to learn more about the domain and understand the design trade-offs.
8.2. Choosing data types and functions
This section will be another messy and iterative process of discovering data types and functions for our library. This time around, we’re designing a library for property-based testing. As before, this is a chance to peer over the shoulder of someone working through possible designs. The particular path we take and the library we arrive at isn’t necessarily the same as what you would come up with on your own. If property-based testing is unfamiliar to you, even better; this is a chance to explore a new domain and its design space, and make your own discoveries about it. If at any point you’re feeling inspired or have ideas of your own about how to design a library like this, don’t wait for an exercise to prompt you—put the book down and go off to play with your ideas. You can always come back to the chapter if you run out of ideas or get stuck.
8.2.1. Initial snippets of an API
With that said, let’s get started. What data types should we use for our testing library? What primitives should we define, and what might they mean? What laws should our functions satisfy? As before, we can look at a simple example and “read off” the needed data types and functions, and see what we find. For inspiration, let’s look at the ScalaCheck example we showed earlier:
val intList = Gen.listOf(Gen.choose(0,100))
val prop =
forAll(intList)(ns => ns.reverse.reverse == ns) &&
forAll(intList)(ns => ns.headOption == ns.reverse.lastOption)
Without knowing anything about the implementation of Gen.choose or Gen.listOf, we can guess that whatever data type they return (let’s call it Gen, short for generator) must be parametric in some type. That is, Gen.choose(0,100) probably returns a Gen[Int], and Gen.listOf is then a function with the signature Gen[Int] => Gen[List[Int]]. But since it doesn’t seem like Gen.listOf should care about the type of the Gen it receives as input (it would be odd to require separate combinators for creating lists of Int, Double, String, and so on), let’s go ahead and make it polymorphic:
def listOf[A](a: Gen[A]): Gen[List[A]]
We can learn many things by looking at this signature. Notice what we’re not specifying—the size of the list to generate. For this to be implementable, our generator must therefore either assume or be told the size. Assuming a size seems a bit inflexible—any assumption is unlikely to be appropriate in all contexts. So it seems that generators must be told the size of test cases to generate. We can imagine an API where this is made explicit:
def listOfN[A](n: Int, a: Gen[A]): Gen[List[A]]
This would certainly be a useful combinator, but not having to explicitly specify sizes is powerful as well. It means that whatever function runs the tests has the freedom to choose test case sizes, which opens up the possibility of doing the test case minimization we mentioned earlier. If the sizes are always fixed and specified by the programmer, the test runner won’t have this flexibility. Keep this concern in mind as we get further along in our design.
What about the rest of this example? The forAll function looks interesting. We can see that it accepts a Gen[List[Int]] and what looks to be a corresponding predicate, List[Int] => Boolean. But again, it doesn’t seem like forAll should care about the types of the generator and the predicate, as long as they match up. We can express this with the type:
def forAll[A](a: Gen[A])(f: A => Boolean): Prop
Here, we’ve simply invented a new type, Prop (short for property, following the ScalaCheck naming), for the result of binding a Gen to a predicate. We might not know the internal representation of Prop or what other functions it supports, but based on this example we can see that it has an&& operator, so let’s introduce that:
trait Prop { def &&(p: Prop): Prop }
8.2.2. The meaning and API of properties
Now that we have a few fragments of an API, let’s discuss what we want our types and functions to mean. First, consider Prop. We know there exist functions forAll (for creating a property), && (for composing properties), and check (for running a property). In ScalaCheck, this checkmethod has a side effect of printing to the console. It’s fine to expose this as a convenience function, but it’s not a basis for composition. For instance, we couldn’t implement && for Prop if its representation were just the check method:[3]
3 This might remind you of similar problems that we discussed in chapter 7, when we looked at using Thread and Runnable for parallelism.
trait Prop {
def check: Unit
def &&(p: Prop): Prop = ???
}
Since check has a side effect, the only option for implementing && in this case would be to run both check methods. So if check prints out a test report, then we would get two of them, and they would print failures and successes independently of each other. That’s likely not a correct implementation. The problem is not so much that check has a side effect, but more generally that it throws away information.
In order to combine Prop values using combinators like &&, we need check (or whatever function “runs” properties) to return some meaningful value. What type should that value have? Well, let’s consider what sort of information we’d like to get out of checking our properties. At a minimum, we need to know whether the property succeeded or failed. This lets us implement &&.
Exercise 8.3
![]()
Assuming the following representation of Prop, implement && as a method of Prop.
trait Prop { def check: Boolean }
In this representation, Prop is nothing more than a non-strict Boolean, and any of the usual Boolean functions (AND, OR, NOT, XOR, and so on) can be defined for Prop. But a Boolean alone is probably insufficient. If a property fails, we might want to know how many tests succeeded first, and what arguments produced the failure. And if a property succeeds, it would be useful to know how many tests it ran. Let’s try returning an Either to indicate success or failure:
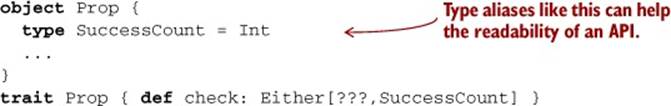
What type shall we return in the failure case? We don’t know anything about the type of the test cases being generated. Should we add a type parameter to Prop and make it Prop[A]? Then check could return Either[A,Int]. Before going too far down this path, let’s ask ourselves whether we really care about the type of the value that caused the property to fail. We don’t really. We would only care about the type if we were going to do further computation with the failure. Most likely we’re just going to end up printing it to the screen for inspection by the person running the tests. After all, the goal here is to find bugs, and to indicate to someone what test cases trigger those bugs so they can go and fix them. As a general rule, we shouldn’t use String to represent data that we want to compute with. But for values that we’re just going to show to human beings, a String is absolutely appropriate. This suggests that we can get away with the following representation for Prop:
object Prop {
type FailedCase = String
type SuccessCount = Int
}
trait Prop {
def check: Either[(FailedCase, SuccessCount), SuccessCount]
}
In the case of failure, check returns a Left((s,n)), where s is some String that represents the value that caused the property to fail, and n is the number of cases that succeeded before the failure occurred.
That takes care of the return value of check, at least for now, but what about the arguments to check? Right now, the check method takes no arguments. Is this sufficient? We can think about what information Prop will have access to just by inspecting the way Prop values are created. In particular, let’s look at forAll:
def forAll[A](a: Gen[A])(f: A => Boolean): Prop
Without knowing more about the representation of Gen, it’s hard to say whether there’s enough information here to be able to generate values of type A (which is what we need to implement check). So for now let’s turn our attention to Gen, to get a better idea of what it means and what its dependencies might be.
8.2.3. The meaning and API of generators
We determined earlier that a Gen[A] was something that knows how to generate values of type A. What are some ways it could do that? Well, it could randomly generate these values. Look back at the example from chapter 6—there, we gave an interface for a purely functional random number generator RNG and showed how to make it convenient to combine computations that made use of it. We could just make Gen a type that wraps a State transition over a random number generator:[4]
4 Recall the definition: case class State[S,A](run: S => (A,S)).
case class Gen[A](sample: State[RNG,A])
Exercise 8.4
![]()
Implement Gen.choose using this representation of Gen. It should generate integers in the range start to stopExclusive. Feel free to use functions you’ve already written.
def choose(start: Int, stopExclusive: Int): Gen[Int]
Exercise 8.5
![]()
Let’s see what else we can implement using this representation of Gen. Try implementing unit, boolean, and listOfN.

As we discussed in chapter 7, we’re interested in understanding what operations are primitive and what operations are derived, and in finding a small yet expressive set of primitives. A good way to explore what is expressible with a given set of primitives is to pick some concrete examples you’d like to express, and see if you can assemble the functionality you want. As you do so, look for patterns, try factoring out these patterns into combinators, and refine your set of primitives. We encourage you to stop reading here and simply play with the primitives and combinators we’ve written so far. If you want some concrete examples to inspire you, here are some ideas:
· If we can generate a single Int in some range, do we need a new primitive to generate an (Int,Int) pair in some range?
· Can we produce a Gen[Option[A]] from a Gen[A]? What about a Gen[A] from a Gen[Option[A]]?
· Can we generate strings somehow using our existing primitives?
The importance of play
You don’t have to wait around for a concrete example to force exploration of the design space. In fact, if you rely exclusively on concrete, obviously useful or important examples to design your API, you’ll often miss out on aspects of the design space and generate APIs with ad hoc, overly specific features. We don’t want to overfit our design to the particular examples we happen to think of right now. We want to reduce the problem to its essence, and sometimes the best way to do this is play. Don’t try to solve important problems or produce useful functionality. Not right away. Just experiment with different representations, primitives, and operations, let questions naturally arise, and explore whatever piques your curiosity. (“These two functions seem similar. I wonder if there’s some more general operation hiding inside,” or “Would it make sense to make this data type polymorphic?” or “What would it mean to change this aspect of the representation from a single value to a List of values?”) There’s no right or wrong way to do this, but there are so many different design choices that it’s impossible not to run headlong into fascinating questions to play with. It doesn’t matter where you begin—if you keep playing, the domain will inexorably guide you to make all the design choices that are required.
8.2.4. Generators that depend on generated values
Suppose we’d like a Gen[(String,String)] that generates pairs where the second string contains only characters from the first. Or that we had a Gen[Int] that chooses an integer between 0 and 11, and we’d like to make a Gen[List[Double]] that then generates lists of whatever length is chosen. In both of these cases there’s a dependency—we generate a value, and then use that value to determine what generator to use next. For this we need flatMap, which lets one generator depend on another.
Exercise 8.6
![]()
Implement flatMap, and then use it to implement this more dynamic version of listOfN. Put flatMap and listOfN in the Gen class.
def flatMap[B](f: A => Gen[B]): Gen[B]
def listOfN(size: Gen[Int]): Gen[List[A]]
Exercise 8.7
![]()
Implement union, for combining two generators of the same type into one, by pulling values from each generator with equal likelihood.
def union[A](g1: Gen[A], g2: Gen[A]): Gen[A]
Exercise 8.8
![]()
Implement weighted, a version of union that accepts a weight for each Gen and generates values from each Gen with probability proportional to its weight.
def weighted[A](g1: (Gen[A],Double), g2: (Gen[A],Double)): Gen[A]
8.2.5. Refining the Prop data type
Now that we know more about our representation of generators, let’s return to our definition of Prop. Our Gen representation has revealed information about the requirements for Prop. Our current definition of Prop looks like this:
trait Prop {
def check: Either[(FailedCase, SuccessCount), SuccessCount]
}
Prop is nothing more than a non-strict Either. But it’s missing some information. We have the number of successful test cases in SuccessCount, but we haven’t specified how many test cases to examine before we consider the property to have passed the test. We could certainly hardcode something, but it would be better to abstract over this dependency:
type TestCases = Int
type Result = Either[(FailedCase, SuccessCount), SuccessCount]
case class Prop(run: TestCases => Result)
Also, we’re recording the number of successful tests on both sides of that Either. But when a property passes, it’s implied that the number of passed tests will be equal to the argument to run. So the caller of run learns nothing new by being told the success count. Since we don’t currently need any information in the Right case of that Either, we can turn it into an Option:
type Result = Option[(FailedCase, SuccessCount)]
case class Prop(run: TestCases => Result)
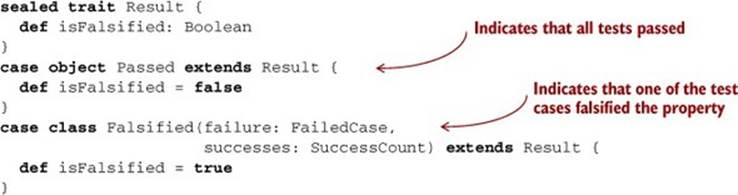
This seems a little weird, since None will mean that all tests succeeded and the property passed and Some will indicate a failure. Until now, we’ve only used the None case of Option to indicate failure. But in this case we’re using it to represent the absence of a failure. That’s a perfectly legitimate use for Option, but its intent isn’t very clear. So let’s make a new data type, equivalent to Option[(FailedCase, SuccessCount)], that shows our intent very clearly.
Listing 8.2. Creating a Result data type
Is this now a sufficient representation of Prop? Let’s take another look at forAll. Can forAll be implemented? Why not?
def forAll[A](a: Gen[A])(f: A => Boolean): Prop
We can see that forAll doesn’t have enough information to return a Prop. Besides the number of test cases to try, Prop.run must have all the information needed to generate test cases. If it needs to generate random test cases using our current representation of Gen, it’s going to need anRNG. Let’s go ahead and propagate that dependency to Prop:
case class Prop(run: (TestCases,RNG) => Result)
If we think of other dependencies that it might need, besides the number of test cases and the source of randomness, we can just add these as extra parameters to Prop.run later.
We now have enough information to actually implement forAll. Here’s a simple implementation.
Listing 8.3. Implementing forAll

Notice that we’re catching exceptions and reporting them as test failures, rather than letting the run throw the error (which would lose information about what argument triggered the failure).
Exercise 8.9
![]()
Now that we have a representation of Prop, implement && and || for composing Prop values. Notice that in the case of failure we don’t know which property was responsible, the left or the right. Can you devise a way of handling this, perhaps by allowing Prop values to be assigned a tag or label which gets displayed in the event of a failure?
def &&(p: Prop): Prop
def ||(p: Prop): Prop
8.3. Test case minimization
Earlier, we mentioned the idea of test case minimization. That is, ideally we’d like our framework to find the smallest or simplest failing test case, to better illustrate the problem and facilitate debugging. Let’s see if we can tweak our representations to support this outcome. There are two general approaches we could take:
· Shrinking —After we’ve found a failing test case, we can run a separate procedure to minimize the test case by successively decreasing its “size” until it no longer fails. This is called shrinking, and it usually requires us to write separate code for each data type to implement this minimization process.
· Sized generation —Rather than shrinking test cases after the fact, we simply generate our test cases in order of increasing size and complexity. So we start small and increase the size until we find a failure. This idea can be extended in various ways to allow the test runner to make larger jumps in the space of possible sizes while still making it possible to find the smallest failing test.
ScalaCheck, incidentally, takes the first approach: shrinking. There’s nothing wrong with this approach (it’s also used by the Haskell library QuickCheck that ScalaCheck is based on: http://mng.bz/E24n), but we’ll see what we can do with sized generation. It’s a bit simpler and in some ways more modular, because our generators only need to know how to generate a test case of a given size. They don’t need to be aware of the “schedule” used to search the space of test cases, and the function that runs the tests therefore has the freedom to choose this schedule. We’ll see how this plays out shortly.
Instead of modifying our Gen data type, for which we’ve already written a number of useful combinators, let’s introduce sized generation as a separate layer in our library. A simple representation of a sized generator is just a function that takes a size and produces a generator:
case class SGen[+A](forSize: Int => Gen[A])
Exercise 8.10
![]()
Implement helper functions for converting Gen to SGen. You can add this as a method on Gen.
def unsized: SGen[A]
Exercise 8.11
![]()
Not surprisingly, SGen at a minimum supports many of the same operations as Gen, and the implementations are rather mechanical. Define some convenience functions on SGen that simply delegate to the corresponding functions on Gen.[5]
5 In part 3 we’ll discuss ways of factoring out this sort of duplication.
Exercise 8.12
![]()
Implement a listOf combinator that doesn’t accept an explicit size. It should return an SGen instead of a Gen. The implementation should generate lists of the requested size.
def listOf[A](g: Gen[A]): SGen[List[A]]
Let’s see how SGen affects the definition of Prop and Prop.forAll. The SGen version of forAll looks like this:
def forAll[A](g: SGen[A])(f: A => Boolean): Prop
Can you see why it’s not possible to implement this function? SGen is expecting to be told a size, but Prop doesn’t receive any size information. Much like we did with the source of randomness and number of test cases, we simply need to add this as a dependency to Prop. But since we want to put Prop in charge of invoking the underlying generators with various sizes, we’ll have Prop accept a maximum size. Prop will then generate test cases up to and including the maximum specified size. This will also allow it to search for the smallest failing test case. Let’s see how this works out.[6]
6 This rather simplistic implementation gives an equal number of test cases to each size being generated, and increases the size by 1 starting from 0. We could imagine a more sophisticated implementation that does something more like a binary search for a failing test case size—starting with sizes 0,1,2,4,8,16..., and then narrowing the search space in the event of a failure.
Listing 8.4. Generating test cases up to a given maximum size

8.4. Using the library and improving its usability
We’ve converged on what seems like a reasonable API. We could keep tinkering with it, but at this point let’s try using the library to construct tests and see if we notice any deficiencies, either in what it can express or in its general usability. Usability is somewhat subjective, but we generally like to have convenient syntax and appropriate helper functions for common usage patterns. We aren’t necessarily aiming to make the library more expressive, but we want to make it pleasant to use.
8.4.1. Some simple examples
Let’s revisit an example that we mentioned at the start of this chapter—specifying the behavior of the function max, available as a method on List (API docs link: http://mng.bz/Pz86). The maximum of a list should be greater than or equal to every other element in the list. Let’s specify this:

At this point, calling run directly on a Prop is rather cumbersome. We can introduce a helper function for running our Prop values and printing their result to the console in a useful format. Let’s make this a method on the Prop companion object.
Listing 8.5. A run helper function for Prop

We’re taking advantage of default arguments here. This makes the method more convenient to call. We want the default number of tests to be enough to get good coverage, but not too many or they’ll take too long to run.
If we try running run(maxProp), we notice that the property fails! Property-based testing has a way of revealing hidden assumptions that we have about our code, and forcing us to be more explicit about these assumptions. The standard library’s implementation of max crashes when given the empty list. We need to fix our property to take this into account.
Exercise 8.13
![]()
Define listOf1 for generating nonempty lists, and then update your specification of max to use this generator.
Let’s try a few more examples.
Exercise 8.14
![]()
Write a property to verify the behavior of List.sorted (API docs link: http://mng.bz/Pz86), which you can use to sort (among other things) a List[Int].[7] For instance, List(2,1,3).sorted is equal to List(1,2,3).
7 sorted takes an implicit Ordering for the elements of the list, to control the sorting strategy.
8.4.2. Writing a test suite for parallel computations
Recall that in chapter 7 we discovered laws that should hold for our parallel computations. Can we express these laws with our library? The first “law” we looked at was actually a particular test case:
map(unit(1))(_ + 1) == unit(2)
We certainly can express this, but the result is somewhat ugly.[8]
8 This is assuming our representation of Par[A] that’s just an alias for the function type ExecutorService => Future[A].
val ES: ExecutorService = Executors.newCachedThreadPool
val p1 = Prop.forAll(Gen.unit(Par.unit(1)))(i =>
Par.map(i)(_ + 1)(ES).get == Par.unit(2)(ES).get)
We’ve expressed the test, but it’s verbose, cluttered, and the idea of the test is obscured by details that aren’t really relevant here. Notice that this isn’t a question of the API being expressive enough—yes, we can express what we want, but a combination of missing helper functions and poor syntax obscures the intent.
Proving Properties
Let’s improve on this. Our first observation is that forAll is a bit too general for this test case. We aren’t varying the input to this test, we just have a hardcoded example. Hardcoded examples should be just as convenient to write as in a traditional unit testing library. Let’s introduce a combinator for it (on the Prop companion object):
def check(p: => Boolean): Prop
How would we implement this? One possible way is to use forAll:
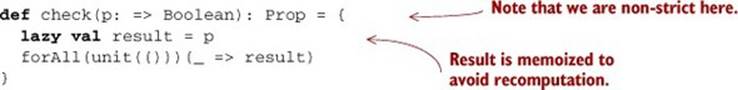
But this doesn’t seem quite right. We’re providing a unit generator that only generates a single value, and then we’re proceeding to ignore that value just to drive the evaluation of the given Boolean.
Even though we memoize the result so that it’s not evaluated more than once, the test runner will still generate multiple test cases and test the Boolean multiple times. For example, if we say run(check(true)), this will test the property 100 times and print “OK, passed 100 tests.” But checking a property that is always true 100 times is a terrible waste of effort. What we need is a new primitive.
Remember, the representation of Prop that we have so far is just a function of type (MaxSize, TestCases, RNG) => Result, where Result is either Passed or Falsified. A simple implementation of a check primitive is to construct a Prop that ignores the number of test cases:
def check(p: => Boolean): Prop = Prop { (_, _, _) =>
if (p) Passed else Falsified("()", 0)
}
This is certainly better than using forAll, but run(check(true)) will still print “passed 100 tests” even though it only tests the property once. It’s not really true that such a property has “passed” in the sense that it remains unfalsified after a number of tests. It is proved after just one test. It seems that we want a new kind of Result:
case object Proved extends Result
Then we can just return Proved instead of Passed in a property created by check. We’ll need to modify the test runner to take this case into account.
Listing 8.6. Using run to return a Proved object
def run(p: Prop,
maxSize: Int = 100,
testCases: Int = 100,
rng: RNG = RNG.Simple(System.currentTimeMillis)): Unit =
p.run(maxSize, testCases, rng) match {
case Falsified((msg, n)) =>
println(s"! Falsified after $n passed tests:\n $msg")
case Passed =>
println(s"+ OK, passed $testCases tests.")
case Proved =>
println(s"+ OK, proved property.")
}
We also have to modify our implementations of Prop combinators like &&. These changes are quite trivial, since such combinators don’t need to distinguish between Passed and Proved results.
Exercise 8.15
![]()
Hard: A check property is easy to prove conclusively because the test just involves evaluating the Boolean argument. But some forAll properties can be proved as well. For instance, if the domain of the property is Boolean, then there are really only two cases to test. If a propertyforAll(p) passes for both p(true) and p(false), then it is proved. Some domains (like Boolean and Byte) are so small that they can be exhaustively checked. And with sized generators, even infinite domains can be exhaustively checked up to the maximum size. Automated testing is very useful, but it’s even better if we can automatically prove our code correct. Modify our library to incorporate this kind of exhaustive checking of finite domains and sized generators. This is less of an exercise and more of an extensive, open-ended design project.
Testing Par
Getting back to proving the property that Par.map(Par.unit(1))(_ + 1) is equal to Par.unit(2), we can use our new Prop.check primitive to express this in a way that doesn’t obscure the intent:
val p2 = Prop.check {
val p = Par.map(Par.unit(1))(_ + 1)
val p2 = Par.unit(2)
p(ES).get == p2(ES).get
}
This is now pretty clear. But can we do something about the p(ES).get and p2(ES).get noise? There’s something rather unsatisfying about it. For one, we’re forcing this code to be aware of the internal implementation details of Par simply to compare two Par values for equality. One improvement is to lift the equality comparison into Par using map2, which means we only have to run a single Par at the end to get our result:
def equal[A](p: Par[A], p2: Par[A]): Par[Boolean] =
Par.map2(p,p2)(_ == _)
val p3 = check {
equal(
Par.map(Par.unit(1))(_ + 1),
Par.unit(2)
)(ES).get
}
This is a bit nicer than having to run each side separately. But while we’re at it, why don’t we move the running of Par out into a separate function, forAllPar. This also gives us a good place to insert variation across different parallel strategies, without it cluttering up the property we’re specifying:

S.map2(g)((_,_)) is a rather noisy way of combining two generators to produce a pair of their outputs. Let’s quickly introduce a combinator to clean that up:[9]
9 Calling this ** is actually appropriate, since this function is taking the product of two generators, in the sense we discussed in chapter 3.
def **[B](g: Gen[B]): Gen[(A,B)] =
(this map2 g)((_,_))
Much nicer:
def forAllPar[A](g: Gen[A])(f: A => Par[Boolean]): Prop =
forAll(S ** g) { case (s,a) => f(a)(s).get }
We can even introduce ** as a pattern using custom extractors (http://mng.bz/4pUc), which lets us write this:
def forAllPar[A](g: Gen[A])(f: A => Par[Boolean]): Prop =
forAll(S ** g) { case s ** a => f(a)(s).get }
This syntax works nicely when tupling up multiple generators—when pattern matching, we don’t have to nest parentheses like using the tuple pattern directly would require. To enable ** as a pattern, we define an object called ** with an unapply function:
object ** {
def unapply[A,B](p: (A,B)) = Some(p)
}
See the custom extractors documentation for more details on this technique.
So S is a Gen[ExecutorService] that will vary over fixed-size thread pools from 1–4 threads, and also consider an unbounded thread pool. And now our property looks a lot cleaner:[10]
10 We can’t use the standard Java/Scala equals method, or the == method in Scala (which delegates to the equals method), since that method returns a Boolean directly, and we need to return a Par[Boolean]. Some infix syntax for equal might be nice. See the answer file for chapter 7 for an example of how to do this.
val p2 = checkPar {
equal (
Par.map(Par.unit(1))(_ + 1),
Par.unit(2)
)
}
These might seem like minor changes, but this sort of factoring and cleanup can greatly improve the usability of our library, and the helper functions we’ve written make the properties easier to read and more pleasant to write. You may want to add a forAllPar version for sized generators as well.
Let’s look at some other properties from chapter 7. Recall that we generalized our test case:
map(unit(x))(f) == unit(f(x))
We then simplified it to the law that mapping the identity function over a computation should have no effect:
map(y)(x => x) == y
Can we express this? Not exactly. This property implicitly states that the equality holds for all choices of y, for all types. We’re forced to pick particular values for y:
val pint = Gen.choose(0,10) map (Par.unit(_))
val p4 =
forAllPar(pint)(n => equal(Par.map(n)(y => y), n))
We can certainly range over more choices of y, but what we have here is probably good enough. The implementation of map can’t care about the values of our parallel computation, so there isn’t much point in constructing the same test for Double, String, and so on. What can affect map is the structure of the parallel computation. If we wanted greater assurance that our property held, we could provide richer generators for the structure. Here, we’re only supplying Par expressions with one level of nesting.
Exercise 8.16
![]()
Hard: Write a richer generator for Par[Int], which builds more deeply nested parallel computations than the simple ones we gave previously.
Exercise 8.17
![]()
Express the property about fork from chapter 7, that fork(x) == x.
8.5. Testing higher-order functions and future directions
So far, our library seems quite expressive, but there’s one area where it’s lacking: we don’t currently have a good way to test higher-order functions. While we have lots of ways of generating data using our generators, we don’t really have a good way of generating functions.
For instance, let’s consider the takeWhile function defined for List and Stream. Recall that this function returns the longest prefix of its input whose elements all satisfy a predicate. For instance, List(1,2,3).takeWhile(_ < 3) results in List(1,2). A simple property we’d like to check is that for any list, s: List[A], and any f: A => Boolean, the expression s.takeWhile(f).forall(f) evaluates to true. That is, every element in the returned list satisfies the predicate.[11]
11 In the Scala standard library, forall is a method on List and Stream with the signature def forall[A] (f: A => Boolean): Boolean.
Exercise 8.18
![]()
Come up with some other properties that takeWhile should satisfy. Can you think of a good property expressing the relationship between takeWhile and dropWhile?
We could certainly take the approach of only examining particular arguments when testing higher-order functions. For instance, here’s a more specific property for takeWhile:
val isEven = (i: Int) => i%2 == 0
val takeWhileProp =
Prop.forAll(Gen.listOf(int))(ns => ns.takeWhile(isEven).forall(isEven))
This works, but is there a way we could let the testing framework handle generating functions to use with takeWhile?[12] Let’s consider our options. To make this concrete, let’s suppose we have a Gen[Int] and would like to produce a Gen[String => Int]. What are some ways we could do that? Well, we could produce String => Int functions that simply ignore their input string and delegate to the underlying Gen[Int]:
12 Recall that in chapter 7 we introduced the idea of free theorems and discussed how parametricity frees us from having to inspect the behavior of a function for every type of argument. Still, there are many situations where being able to generate functions for testing is useful.
def genStringIntFn(g: Gen[Int]): Gen[String => Int] =
g map (i => (s => i))
This approach isn’t sufficient though. We’re simply generating constant functions that ignore their input. In the case of takeWhile, where we need a function that returns a Boolean, this will be a function that always returns true or always returns false—clearly not very interesting for testing the behavior of our function.
Exercise 8.19
![]()
Hard: We want to generate a function that uses its argument in some way to select which Int to return. Can you think of a good way of expressing this? This is a very open-ended and challenging design exercise. See what you can discover about this problem and if there’s a nice general solution that you can incorporate into the library we’ve developed so far.
Exercise 8.20
![]()
You’re strongly encouraged to venture out and try using the library we’ve developed! See what else you can test with it, and see if you discover any new idioms for its use or perhaps ways it could be extended further or made more convenient. Here are a few ideas to get you started:
· Write properties to specify the behavior of some of the other functions we wrote for List and Stream, for instance, take, drop, filter, and unfold.
· Write a sized generator for producing the Tree data type defined in chapter 3, and then use this to specify the behavior of the fold function we defined for Tree. Can you think of ways to improve the API to make this easier?
· Write properties to specify the behavior of the sequence function we defined for Option and Either.
8.6. The laws of generators
Isn’t it interesting that many of the functions we’ve implemented for our Gen type look quite similar to other functions we defined on Par, List, Stream, and Option? As an example, for Par we defined this:
def map[A,B](a: Par[A])(f: A => B): Par[B]
And in this chapter we defined map for Gen (as a method on Gen[A]):
def map[B](f: A => B): Gen[B]
We’ve also defined similar-looking functions for Option, List, Stream, and State. We have to wonder, is it merely that our functions share similar-looking signatures, or do they satisfy the same laws as well? Let’s look at a law we introduced for Par in chapter 7:
map(x)(id) == x
Does this law hold for our implementation of Gen.map? What about for Stream, List, Option, and State? Yes, it does! Try it and see. This indicates that not only do these functions share similar-looking signatures, they also in some sense have analogous meanings in their respective domains. It appears there are deeper forces at work! We’re uncovering some fundamental patterns that cut across domains. In part 3, we’ll learn the names for these patterns, discover the laws that govern them, and understand what it all means.
8.7. Summary
In this chapter, we worked through another extended exercise in functional library design, using the domain of property-based testing as inspiration.
We reiterate that our goal was not necessarily to learn about property-based testing as such, but to highlight particular aspects of functional design. First, we saw that oscillating between the abstract algebra and the concrete representation lets the two inform each other. This avoids overfitting the library to a particular representation, and also avoids ending up with a floating abstraction disconnected from the end goal.
Second, we noticed that this domain led us to discover many of the same combinators we’ve now seen a few times before: map, flatMap, and so on. Not only are the signatures of these functions analogous, the laws satisfied by the implementations are analogous too. There are a great many seemingly distinct problems being solved in the world of software, yet the space of functional solutions is much smaller. Many libraries are just simple combinations of certain fundamental structures that appear over and over again across a variety of different domains. This is an opportunity for code reuse that we’ll exploit in part 3, when we learn both the names of some of these structures and how to spot more general abstractions.
In the next and final chapter of part 2, we’ll look at another domain, parsing, with its own unique challenges. We’ll take a slightly different approach in that chapter, but once again familiar patterns will emerge.