Data Science from Scratch: First Principles with Python (2015)
Chapter 18. Neural Networks
I like nonsense; it wakes up the brain cells.
Dr. Seuss
Perceptrons
defstep_function(x):
return1ifx>=0else0
defperceptron_output(weights,bias,x):
"""returns 1 if the perceptron 'fires', 0 if not"""
calculation=dot(weights,x)+bias
returnstep_function(calculation)
dot(weights,x)+bias==0
weights=[2,2]
bias=-3
weights=[2,2]
bias=-1
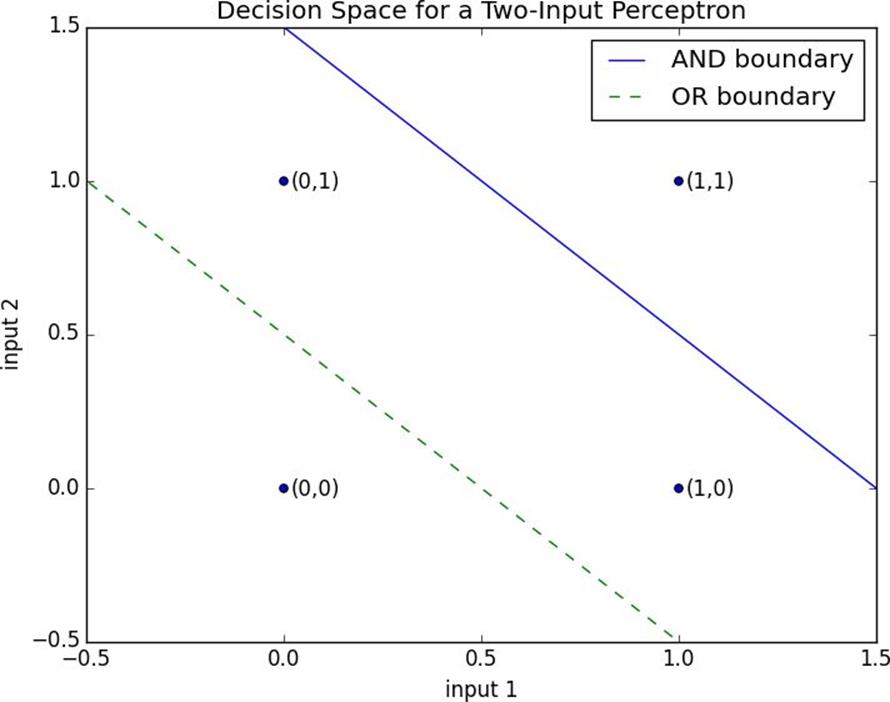
Figure 18-1. Decision space for a two-input perceptron
weights=[-2]
bias=1
and_gate=min
or_gate=max
xor_gate=lambdax,y:0ifx==yelse1
Feed-Forward Neural Networks
defsigmoid(t):
return1/(1+math.exp(-t))
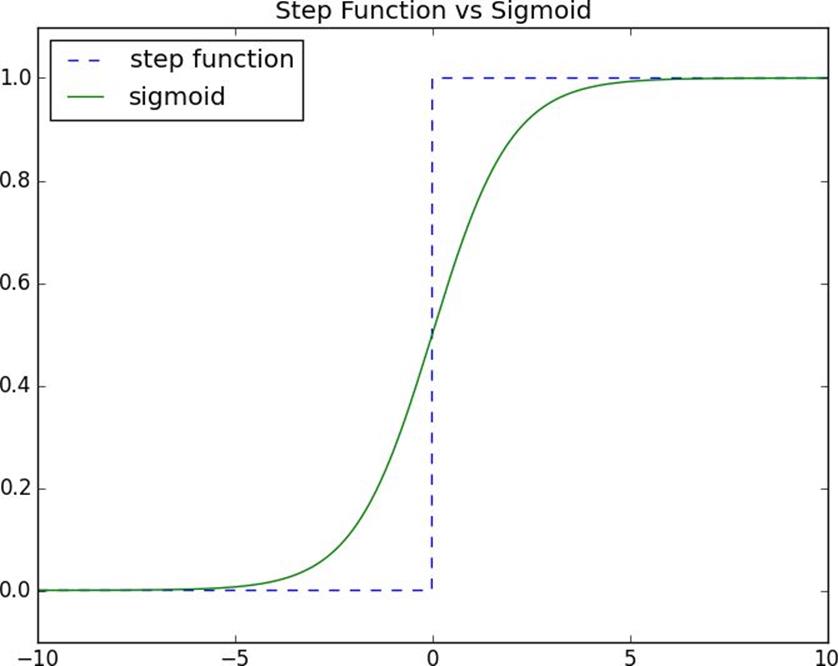
Figure 18-2. The sigmoid function
NOTE
defneuron_output(weights,inputs):
returnsigmoid(dot(weights,inputs))
deffeed_forward(neural_network,input_vector):
"""takes in a neural network
(represented as a list of lists of lists of weights) and returns the output from forward-propagating the input"""outputs=[]
# process one layer at a time
forlayerinneural_network:
input_with_bias=input_vector+[1]# add a bias input
output=[neuron_output(neuron,input_with_bias)# compute the output
forneuroninlayer]# for each neuron
outputs.append(output)# and remember it
# then the input to the next layer is the output of this one
input_vector=output
returnoutputs
xor_network=[# hidden layer
[[20,20,-30],# 'and' neuron
[20,20,-10]],# 'or' neuron
# output layer
[[-60,60,-30]]]# '2nd input but not 1st input' neuron
forxin[0,1]:
foryin[0,1]:
# feed_forward produces the outputs of every neuron
# feed_forward[-1] is the outputs of the output-layer neurons
x,y,feed_forward(xor_network,[x,y])[-1]
# 0 0 [9.38314668300676e-14]# 0 1 [0.9999999999999059]# 1 0 [0.9999999999999059]# 1 1 [9.383146683006828e-14]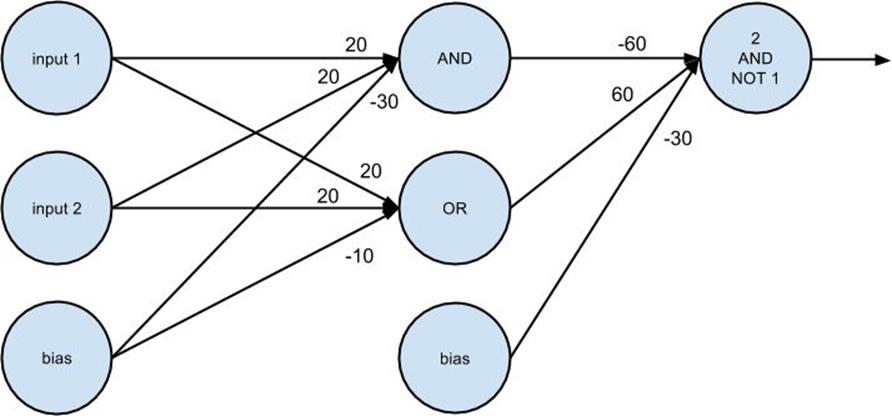
Figure 18-3. A neural network for XOR
1. Run feed_forward on an input vector to produce the outputs of all the neurons in the network.
2. This results in an error for each output neuron — the difference between its output and its target.
3. Compute the gradient of this error as a function of the neuron’s weights, and adjust its weights in the direction that most decreases the error.
4. “Propagate” these output errors backward to infer errors for the hidden layer.
5. Compute the gradients of these errors and adjust the hidden layer’s weights in the same manner.
defbackpropagate(network,input_vector,targets):
hidden_outputs,outputs=feed_forward(network,input_vector)
# the output * (1 - output) is from the derivative of sigmoid
output_deltas=[output*(1-output)*(output-target)
foroutput,targetinzip(outputs,targets)]
# adjust weights for output layer, one neuron at a time
fori,output_neuroninenumerate(network[-1]):
# focus on the ith output layer neuron
forj,hidden_outputinenumerate(hidden_outputs+[1]):
# adjust the jth weight based on both
# this neuron's delta and its jth input
output_neuron[j]-=output_deltas[i]*hidden_output
# back-propagate errors to hidden layer
hidden_deltas=[hidden_output*(1-hidden_output)*
dot(output_deltas,[n[i]forninoutput_layer])
fori,hidden_outputinenumerate(hidden_outputs)]
# adjust weights for hidden layer, one neuron at a time
fori,hidden_neuroninenumerate(network[0]):
forj,inputinenumerate(input_vector+[1]):
hidden_neuron[j]-=hidden_deltas[i]*input
Example: Defeating a CAPTCHA
@@@@@ ..@.. @@@@@ @@@@@ @...@ @@@@@ @@@@@ @@@@@ @@@@@ @@@@@
@...@ ..@.. ....@ ....@ @...@ @.... @.... ....@ @...@ @...@
@...@ ..@.. @@@@@ @@@@@ @@@@@ @@@@@ @@@@@ ....@ @@@@@ @@@@@
@...@ ..@.. @.... ....@ ....@ ....@ @...@ ....@ @...@ ....@
@@@@@ ..@.. @@@@@ @@@@@ ....@ @@@@@ @@@@@ ....@ @@@@@ @@@@@
zero_digit=[1,1,1,1,1,
1,0,0,0,1,
1,0,0,0,1,
1,0,0,0,1,
1,1,1,1,1]
[0,0,0,0,1,0,0,0,0,0]
targets=[[1ifi==jelse0foriinrange(10)]
forjinrange(10)]
random.seed(0)# to get repeatable results
input_size=25# each input is a vector of length 25
num_hidden=5# we'll have 5 neurons in the hidden layer
output_size=10# we need 10 outputs for each input
# each hidden neuron has one weight per input, plus a bias weighthidden_layer=[[random.random()for__inrange(input_size+1)]
for__inrange(num_hidden)]
# each output neuron has one weight per hidden neuron, plus a bias weightoutput_layer=[[random.random()for__inrange(num_hidden+1)]
for__inrange(output_size)]
# the network starts out with random weightsnetwork=[hidden_layer,output_layer]
# 10,000 iterations seems enough to convergefor__inrange(10000):
forinput_vector,target_vectorinzip(inputs,targets):
backpropagate(network,input_vector,target_vector)
defpredict(input):
returnfeed_forward(network,input)[-1]
predict(inputs[7])# [0.026, 0.0, 0.0, 0.018, 0.001, 0.0, 0.0, 0.967, 0.0, 0.0]predict([0,1,1,1,0,# .@@@.
0,0,0,1,1,# ...@@
0,0,1,1,0,# ..@@.
0,0,0,1,1,# ...@@
0,1,1,1,0])# .@@@.
# [0.0, 0.0, 0.0, 0.92, 0.0, 0.0, 0.0, 0.01, 0.0, 0.12]predict([0,1,1,1,0,# .@@@.
1,0,0,1,1,# @..@@
0,1,1,1,0,# .@@@.
1,0,0,1,1,# @..@@
0,1,1,1,0])# .@@@.
# [0.0, 0.0, 0.0, 0.0, 0.0, 0.55, 0.0, 0.0, 0.93, 1.0]importmatplotlib
weights=network[0][0]# first neuron in hidden layer
abs_weights=map(abs,weights)# darkness only depends on absolute value
grid=[abs_weights[row:(row+5)]# turn the weights into a 5x5 grid
forrowinrange(0,25,5)]# [weights[0:5], ..., weights[20:25]]
ax=plt.gca()# to use hatching, we'll need the axis
ax.imshow(grid,# here same as plt.imshow
cmap=matplotlib.cm.binary,# use white-black color scale
interpolation='none')# plot blocks as blocks
defpatch(x,y,hatch,color):
"""return a matplotlib 'patch' object with the specified
location, crosshatch pattern, and color"""returnmatplotlib.patches.Rectangle((x-0.5,y-0.5),1,1,
hatch=hatch,fill=False,color=color)
# cross-hatch the negative weightsforiinrange(5):# row
forjinrange(5):# column
ifweights[5*i+j]<0:# row i, column j = weights[5*i + j]
# add black and white hatches, so visible whether dark or light
ax.add_patch(patch(j,i,'/',"white"))
ax.add_patch(patch(j,i,'\\',"black"))
plt.show()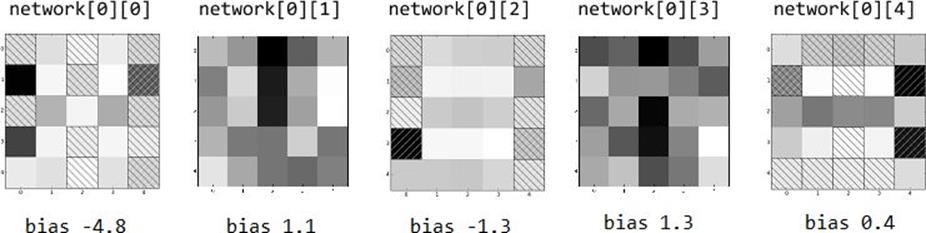
Figure 18-4. Weights for the hidden layer
left_column_only=[1,0,0,0,0]*5
feed_forward(network,left_column_only)[0][0]# 1.0
center_middle_row=[0,0,0,0,0]*2+[0,1,1,1,0]+[0,0,0,0,0]*2
feed_forward(network,center_middle_row)[0][0]# 0.95
right_column_only=[0,0,0,0,1]*5
feed_forward(network,right_column_only)[0][0]# 0.0
my_three=[0,1,1,1,0,# .@@@.
0,0,0,1,1,# ...@@
0,0,1,1,0,# ..@@.
0,0,0,1,1,# ...@@
0,1,1,1,0]# .@@@.
hidden,output=feed_forward(network,my_three)
0.121080 # from network[0][0], probably dinged by (1, 4)
0.999979 # from network[0][1], big contributions from (0, 2) and (2, 2)
0.999999 # from network[0][2], positive everywhere except (3, 4)
0.999992 # from network[0][3], again big contributions from (0, 2) and (2, 2)
0.000000 # from network[0][4], negative or zero everywhere except center row
-11.61 # weight for hidden[0]
-2.17 # weight for hidden[1]
9.31 # weight for hidden[2]
-1.38 # weight for hidden[3]
-11.47 # weight for hidden[4]
- 1.92 # weight for bias input
sigmoid(.121*-11.61+1*-2.17+1*9.31-1.38*1-0*11.47-1.92)
§ Coursera has a free course on Neural Networks for Machine Learning. As I write this it was last run in 2012, but the course materials are still available.
§ Michael Nielsen is writing a free online book on Neural Networks and Deep Learning. By the time you read this it might be finished.
§ PyBrain is a pretty simple Python neural network library.
§ Pylearn2 is a much more advanced (and much harder to use) neural network library.
All materials on the site are licensed Creative Commons Attribution-Sharealike 3.0 Unported CC BY-SA 3.0 & GNU Free Documentation License (GFDL)
If you are the copyright holder of any material contained on our site and intend to remove it, please contact our site administrator for approval.
© 2016-2026 All site design rights belong to S.Y.A.