Algorithms (2014)
Two. Sorting
2.4 Priority Queues
MANY APPLICATIONS REQUIRE that we process items having keys in order, but not necessarily in full sorted order and not necessarily all at once. Often, we collect a set of items, then process the one with the largest key, then perhaps collect more items, then process the one with the current largest key, and so forth. For example, you are likely to have a computer (or a cellphone) that is capable of running several applications at the same time. This effect is typically achieved by assigning a priority to events associated with applications, then always choosing to process next the highest-priority event. For example, most cellphones are likely to process an incoming call with higher priority than a game application.
An appropriate data type in such an environment supports two operations: remove the maximum and insert. Such a data type is called a priority queue. Using priority queues is similar to using queues (remove the oldest) and stacks (remove the newest), but implementing them efficiently is more challenging.
In this section, after a short discussion of elementary representations where one or both of the operations take linear time, we consider a classic priority-queue implementation based on the binary heap data structure, where items are kept in an array, subject to certain ordering constraints that allow for efficient (logarithmic-time) implementations of remove the maximum and insert.
Some important applications of priority queues include simulation systems, where the keys correspond to event times, to be processed in chronological order; job scheduling, where the keys correspond to priorities indicating which tasks are to be performed first; and numerical computations, where the keys represent computational errors, indicating in which order we should deal with them. We consider in CHAPTER 6 a detailed case study showing the use of priority queues in a particle-collision simulation.
We can use any priority queue as the basis for a sorting algorithm by inserting a sequence of items, then successively removing the smallest to get them out, in order. An important sorting algorithm known as heapsort also follows naturally from our heap-based priority-queue implementations. Later on in this book, we shall see how to use priority queues as building blocks for other algorithms. In CHAPTER 4, we shall see how priority queues are an appropriate abstraction for implementing several fundamental graph-searching algorithms; in CHAPTER 5, we shall develop a data-compression algorithm using methods from this section. These are but a few examples of the important role played by the priority queue as a tool in algorithm design.
API
The priority queue is a prototypical abstract data type (see SECTION 1.2): it represents a set of values and operations on those values, and it provides a convenient abstraction that allows us to separate application programs (clients) from various implementations that we will consider in this section. As in SECTION 1.2, we precisely define the operations by specifying an applications programming interface (API) that provides the information needed by clients. Priority queues are characterized by the remove the maximum and insert operations, so we shall focus on them. We use the method names delMax() for remove the maximum and insert() for insert. By convention, we will compare keys only with a helper less() method, as we have been doing for sorting. Thus, if items can have duplicate keys, maximum means any item with the largest key value. To complete the API, we also need to add constructors (like the ones we used for stacks and queues) and a test if empty operation. For flexibility, we use a generic implementation with a parameterized type Key that implements the Comparable interface. This choice eliminates our distinction between items and keys and enables clearer and more compact descriptions of data structures and algorithms. For example, we refer to the “largest key” instead of the “largest item” or the “item with the largest key.”
For convenience in client code, the API includes three constructors, which enable clients to build priority queues of an initial fixed size (perhaps initialized with a given array of keys). To clarify client code, we will use a separate class MinPQ whenever appropriate, which is the same as MaxPQexcept that it has a delMin() method that deletes and returns an item with the smallest key in the queue. Any MaxPQ implementation is easily converted into a MinPQ implementation and vice versa, simply by reversing the sense of the comparison in less().
A priority-queue client
To appreciate the value of the priority-queue abstraction, consider the following problem: You have a huge input stream of N strings and associated integer values, and your task is to find the largest or smallest M integers (and associated strings) in the input stream. You might imagine the stream to be financial transactions, where your interest is to find the big ones, or pesticide levels in an agricultural product, where your interest is to find the small ones, or requests for service, or results from a scientific experiment, or whatever. In some applications, the size of the input stream is so huge that it is best to consider it to be unbounded. One way to address this problem would be to sort the input stream and take the M largest keys from the result, but we have just stipulated that the input stream is too large for that. Another approach would be to compare each new key against the M largest seen so far, but that is also likely to be prohibitively expensive unless M is small. With priority queues, we can solve the problem with the MinPQ client TopM on the next page provided that we can develop efficient implementations of both insert() and delMin(). That is precisely our aim in this section. For the huge values of N that are likely to be encountered in our modern computational infrastructure, these implementations can make the difference between being able to address such a problem and not having the resources to do it at all.
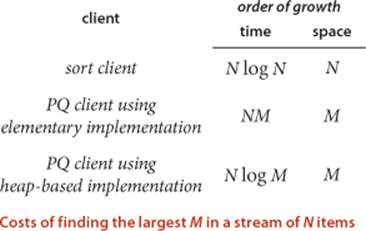
Elementary implementations
The basic data structures that we discussed in CHAPTER 1 provide us with four immediate starting points for implementing priority queues. We can use an array or a linked list, kept in order or unordered. These implementations are useful for small priority queues, situations where one of the two operations are predominant, or situations where some assumptions can be made about the order of the keys involved in the operations. Since these implementations are elementary, we will be content with brief descriptions here in the text and leave the code for exercises (see EXERCISE 2.4.3).
Array representation (unordered)
Perhaps the simplest priority-queue implementation is based on our code for pushdown stacks in SECTION 1.3. The code for insert in the priority queue is the same as for push in the stack. To implement remove the maximum, we can add code like the inner loop of selection sort to exchange the maximum item with the item at the end and then delete that one, as we did with pop() for stacks. As with stacks, we can add resizing-array code to ensure that the data structure is always at least one-quarter full and never overflows.
A priority-queue client
public class TopM
{
public static void main(String[] args)
{ // Print the top M lines in the input stream.
int M = Integer.parseInt(args[0]);
MinPQ<Transaction> pq = new MinPQ<Transaction>(M+1);
while (StdIn.hasNextLine())
{ // Create an entry from the next line and put on the PQ.
pq.insert(new Transaction(StdIn.readLine()));
if (pq.size() > M)
pq.delMin(); // Remove minimum if M+1 entries on the PQ.
} // Top M entries are on the PQ.
Stack<Transaction> stack = new Stack<Transaction>();
while (!pq.isEmpty()) stack.push(pq.delMin());
for (Transaction t : stack) StdOut.println(t);
}
}
Given an integer M from the command line and an input stream where each line contains a transaction, this MinPQ client prints the M lines whose numbers are the highest. It does so by using our Transaction class (see page 79, EXERCISE 1.2.19, and EXERCISE 2.1.21) to build a priority queue using the numbers as keys, deleting the minimum after each insertion once the size of the priority queue reaches M. Once all the transactions have been processed, the top M come off the priority queue in increasing order, so this code puts them on a stack, then iterates through the stack to reverse the order and print them in decreasing order.
% more tinyBatch.txt
Turing 6/17/1990 644.08
vonNeumann 3/26/2002 4121.85
Dijkstra 8/22/2007 2678.40
vonNeumann 1/11/1999 4409.74
Dijkstra 11/18/1995 837.42
Hoare 5/10/1993 3229.27
vonNeumann 2/12/1994 4732.35
Hoare 8/18/1992 4381.21
Turing 1/11/2002 66.10
Thompson 2/27/2000 4747.08
Turing 2/11/1991 2156.86
Hoare 8/12/2003 1025.70
vonNeumann 10/13/1993 2520.97
Dijkstra 9/10/2000 708.95
Turing 10/12/1993 3532.36
Hoare 2/10/2005 4050.20
% java TopM 5 < tinyBatch.txt
Thompson 2/27/2000 4747.08
vonNeumann 2/12/1994 4732.35
vonNeumann 1/11/1999 4409.74
Hoare 8/18/1992 4381.21
vonNeumann 3/26/2002 4121.85
Array representation (ordered)
Another approach is to add code for insert to move larger entries one position to the right, thus keeping the keys in the array in order (as in insertion sort). Thus, the largest entry is always at the end, and the code for remove the maximum in the priority queue is the same as for pop in the stack.
Linked-list representations
Similarly, we can start with our linked-list code for pushdown stacks, modifying either the code for pop() to find and return the maximum or the code for push() to keep keys in reverse order and the code for pop() to unlink and return the first (maximum) item on the list.
Using unordered sequences is the prototypical lazy approach to this problem, where we defer doing work until necessary (to find the maximum); using ordered sequences is the prototypical eager approach to the problem, where we do as much work as we can up front (keep the list sorted on insertion) to make later operations efficient.
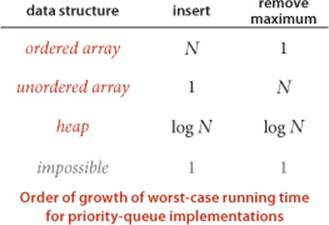
The significant difference between implementing stacks or queues and implementing priority queues has to do with performance. For stacks and queues, we were able to develop implementations of all the operations that take constant time; for priority queues, all of the elementary implementations just discussed have the property that either the insert or the remove the maximum operation takes linear time in the worst case. The heap data structure that we consider next enables implementations where both operations are guaranteed to be fast.
Heap definitions
The binary heap is a data structure that can efficiently support the basic priority-queue operations. In a binary heap, the keys are stored in an array such that each key is guaranteed to be larger than (or equal to) the keys at two other specific positions. In turn, each of those keys must be larger than (or equal to) two additional keys, and so forth. This ordering is easy to see if we view the keys as being in a binary tree structure with edges from each key to the two keys known to be smaller.
Definition. A binary tree is heap-ordered if the key in each node is larger than or equal to the keys in that node’s two children (if any).
Equivalently, the key in each node of a heap-ordered binary tree is smaller than or equal to the key in that node’s parent (if any). Moving up from any node, we get a nondecreasing sequence of keys; moving down from any node, we get a nonincreasing sequence of keys. In particular:
Proposition O. The largest key in a heap-ordered binary tree is found at the root.
Proof: By induction on the size of the tree.
Binary heap representation
If we use a linked representation for heap-ordered binary trees, we would need to have three links associated with each key to allow travel up and down the tree (each node would have one pointer to its parent and one to each child). It is particularly convenient, instead, to use a completebinary tree like the one drawn at right. We draw such a structure by placing the root node and then proceeding down the page and from left to right, drawing and connecting two nodes beneath each node on the previous level until we have drawn N nodes. Complete trees provide the opportunity to use a compact array representation that does not involve explicit links. Specifically, we represent complete binary trees sequentially within an array by putting the nodes in level order, with the root at position 1, its children at positions 2 and 3, their children in positions 4, 5, 6, and 7, and so on.
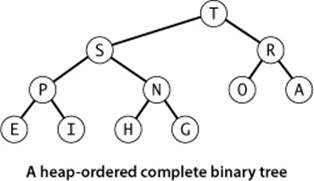
Definition. A binary heap is a collection of keys arranged in a complete heap-ordered binary tree, represented in level order in an array (not using the first entry).
(For brevity, from now on we drop the “binary” modifier and use the term heap when referring to a binary heap.) In a heap, the parent of the node in position k is in position 
k/2
and, conversely, the two children of the node in position k are in positions 2k and 2k + 1. Instead of using explicit links (as in the binary tree structures that we will consider in CHAPTER 3), we can travel up and down by doing simple arithmetic on array indices: to move up the tree from a[k] we set k to k/2; to move down the tree we set k to 2*k or 2*k+1.
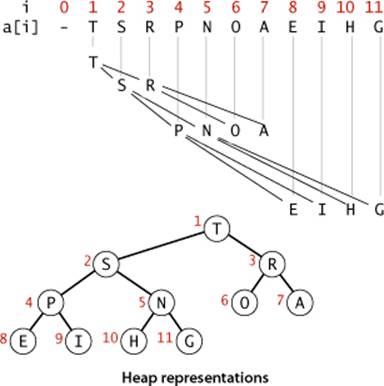
Complete binary trees represented as arrays (heaps) are rigid structures, but they have just enough flexibility to allow us to implement efficient priority-queue operations. Specifically, we will use them to develop logarithmic-time insert and remove the maximum implementations. These algorithms take advantage of the capability to move up and down paths in the tree without pointers and have guaranteed logarithmic performance because of the following property of complete binary trees:
Proposition P. The height of a complete binary tree of size N is lg N .
Proof: The stated result is easy to prove by induction or by noting that the height increases by 1 only when N is incremented to become a power of 2.
Algorithms on heaps
We represent a heap of size N in private array pq[] of length N + 1, with pq[0] unused and the heap in pq[1] through pq[N]. As for sorting algorithms, we access keys only through private helper functions less() and exch(), but since all items are in the instance variable pq[], we use the more compact implementations that do not involve passing the array name as a parameter. The heap operations that we consider work by first making a simple modification that could violate the heap condition, then traveling through the heap, modifying the heap as required to ensure that the heap condition is satisfied everywhere. We refer to this process as reheapifying, or restoring heap order.
Compare and exchange methods for heap implementations
private boolean less(int i, int j)
{ return pq[i].compareTo(pq[j]) < 0; }
private void exch(int i, int j)
{ Key t = pq[i]; pq[i] = pq[j]; pq[j] = t; }
There are two cases. When the priority of some node is increased (or a new node is added at the bottom of a heap), we have to travel up the heap to restore the heap order. When the priority of some node is decreased (for example, if we replace the node at the root with a new node that has a smaller key), we have to travel down the heap to restore the heap order. First, we will consider how to implement these two basic auxiliary operations; then, we shall see how to use them to implement insert and remove the maximum.
Bottom-up reheapify (swim)
If the heap order is violated because a node’s key becomes larger than that node’s parent’s key, then we can make progress toward fixing the violation by exchanging the node with its parent. After the exchange, the node is larger than both its children (one is the old parent, and the other is smaller than the old parent because it was a child of that node) but the node may still be larger than its parent. We can fix that violation in the same way, and so forth, moving up the heap until we reach a node with a larger key, or the root. Coding this process is straightforward when you keep in mind that the parent of the node at position k in a heap is at position k/2. The loop in swim() preserves the invariant that the only place the heap order could be violated is when the node at position k might be larger than its parent. Therefore, when we get to a place where that node is not larger than its parent, we know that the heap order is satisfied throughout the heap. To justify the method’s name, we think of the new node, having too large a key, as having to swim to a higher level in the heap.
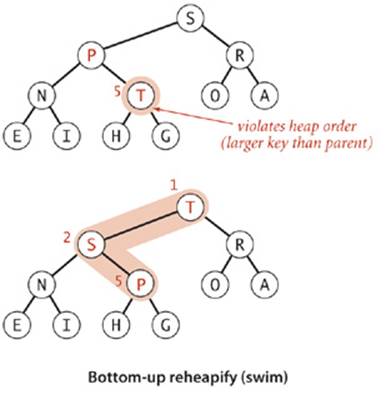
Bottom-up reheapify (swim) implementation
private void swim(int k)
{
while (k > 1 && less(k/2, k))
{
exch(k/2, k);
k = k/2;
}
}
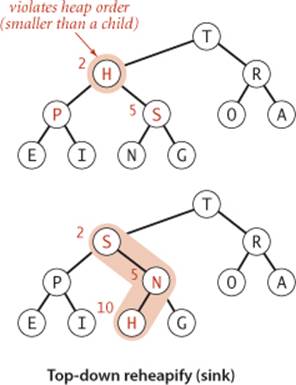
Top-down reheapify (sink)
If the heap order is violated because a node’s key becomes smaller than one or both of that node’s children’s keys, then we can make progress toward fixing the violation by exchanging the node with the larger of its two children. This switch may cause a violation at the child; we fix that violation in the same way, and so forth, moving down the heap until we reach a node with both children smaller (or equal), or the bottom. The code again follows directly from the fact that the children of the node at position k in a heap are at positions 2k and 2k+1. To justify the method’s name, we think about the node, having too small a key, as having to sink to a lower level in the heap.
Top-down reheapify (sink) implementation
private void sink(int k)
{
while (2*k <= N)
{
int j = 2*k;
if (j < N && less(j, j+1)) j++;
if (!less(k, j)) break;
exch(k, j);
k = j;
}
}
IF WE IMAGINE the heap to represent a cutthroat corporate hierarchy, with each of the children of a node representing subordinates (and the parent representing the immediate superior), then these operations have amusing interpretations. The swim() operation corresponds to a promising new manager arriving on the scene, being promoted up the chain of command (by exchanging jobs with any lower-qualified boss) until the new person encounters a higher-qualified boss. The sink() operation is analogous to the situation when the president of the company resigns and is replaced by someone from the outside. If the president’s most powerful subordinate is stronger than the new person, they exchange jobs, and we move down the chain of command, demoting the new person and promoting others until the level of competence of the new person is reached, where there is no higher-qualified subordinate. These idealized scenarios may rarely be seen in the real world, but they may help you better understand basic operation on heaps.
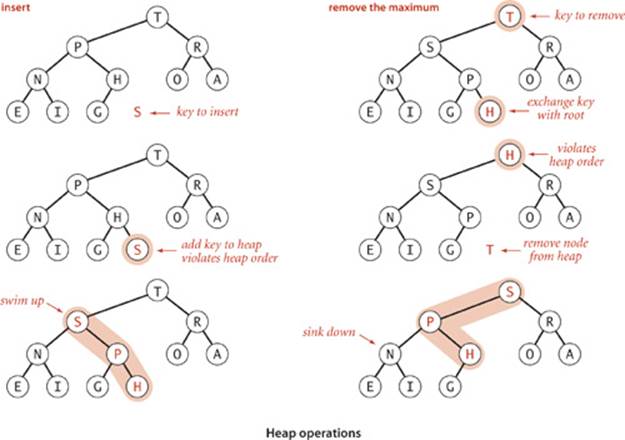
These sink() and swim() operations provide the basis for efficient implementation of the priority-queue API, as diagrammed below and implemented in ALGORITHM 2.6
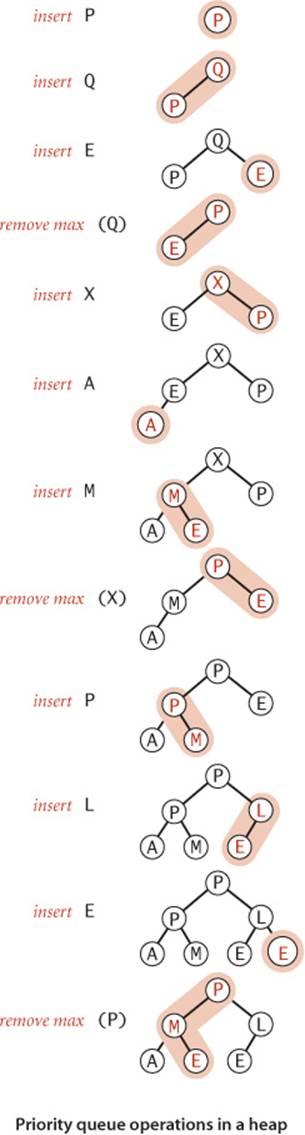
Insert. We add the new key at the end of the array, increment the size of the heap, and then swim up through the heap with that key to restore the heap condition.
Remove the maximum. We take the largest item off the top, put the item from the end of the heap at the top, decrement the size of the heap, and then sink down through the heap with that key to restore the heap condition.
ALGORITHM 2.6 solves the basic problem that we posed at the beginning of this section: it is a priority-queue API implementation for which both insert and delete the maximum are guaranteed to take time logarithmic in the size of the queue.
Algorithm 2.6 Heap priority queue
public class MaxPQ<Key extends Comparable<Key>>
{
private Key[] pq; // heap-ordered complete binary tree
private int N = 0; // in pq[1..N] with pq[0] unused
public MaxPQ(int maxN)
{ pq = (Key[]) new Comparable[maxN+1]; }
public boolean isEmpty()
{ return N == 0; }
public int size()
{ return N; }
public void insert(Key v)
{
pq[++N] = v;
swim(N);
}
public Key delMax()
{
Key max = pq[1]; // Retrieve max key from top.
exch(1, N--); // Exchange with last item.
pq[N+1] = null; // Avoid loitering.
sink(1); // Restore heap property.
return max;
}
// See pages 315-316 for implementations of these helper methods.
private boolean less(int i, int j)
private void exch(int i, int j)
private void swim(int k)
private void sink(int k)
}
The priority queue is maintained in a heap-ordered complete binary tree in the array pq[] with pq[0] unused and the N keys in the priority queue in pq[1] through pq[N]. To implement insert(), we increment N, add the new element at the end, then use swim() to restore the heap order. For delMax(), we take the value to be returned from pq[1], then move pq[N] to pq[1], decrement the size of the heap, and use sink() to restore the heap condition. We also set the now-unused position pq[N+1] to null to allow the system to reclaim the memory associated with it. Code for dynamic array resizing is omitted, as usual (see SECTION 1.3). See EXERCISE 2.4.19 for the other constructors.
Proposition Q. In an N-key priority queue, the heap algorithms require no more than 1 + lg N compares for insert and no more than 2 lg N compares for remove the maximum.
Proof: By PROPOSITION P, both operations involve moving along a path between the root and the bottom of the heap whose number of links is no more than lg N. The remove the maximum operation requires two compares for each node on the path (except at the bottom): one to find the child with the larger key, the other to decide whether that child needs to be promoted.
For typical applications that require a large number of intermixed insert and remove the maximum operations in a large priority queue, PROPOSITION Q represents an important performance breakthrough, summarized in the table shown on page 312. Where elementary implementations using an ordered array or an unordered array require linear time for one of the operations, a heap-based implementation provides a guarantee that both operations complete in logarithmic time. This improvement can make the difference between solving a problem and not being able to address it at all.
Multiway heaps
It is not difficult to modify our code to build heaps based on an array representation of complete heap-ordered ternary trees, with an entry at position k larger than or equal to entries at positions 3k−1, 3k, and 3k+1 and smaller than or equal to entries at position (k+1) / 3, for all indices between 1 and N in an array of N items, and not much more difficult to use d-ary heaps for any given d. There is a tradeoff between the lower cost from the reduced tree height (logd N) and the higher cost of finding the largest of the d children at each node. This tradeoff is dependent on details of the implementation and the expected relative frequency of operations.
Array resizing
We can add a no-argument constructor, code for array doubling in insert(), and code for array halving in delMax(), just as we did for stacks in SECTION 1.3. Thus, clients need not be concerned about arbitrary size restrictions. The logarithmic time bounds implied by PROPOSITION Q are amortizedwhen the size of the priority queue is arbitrary and the arrays are resized (see EXERCISE 2.4.22).
Immutability of keys
The priority queue contains objects that are created by clients but assumes that client code does not change the keys (which might invalidate the heap-order invariant). It is possible to develop mechanisms to enforce this assumption, but programmers typically do not do so because they complicate the code and are likely to degrade performance.
Index priority queue
In many applications, it makes sense to allow clients to refer to items that are already on the priority queue. One easy way to do so is to associate a unique integer index with each item. Moreover, it is often the case that clients have a universe of items of a known size N and perhaps are using (parallel) arrays to store information about the items, so other unrelated client code might already be using an integer index to refer to items. These considerations lead us to the following API:
A useful way of thinking of this data type is as implementing an array, but with fast access to the smallest entry in the array. Actually it does even better—it gives fast access to the minimum entry in a specified subset of an array’s entries (the ones that have been inserted. In other words, you can think of an IndexMinPQ named pq as representing a subset of an array pq[0..N-1] of items. Think of the call pq.insert(i, key) as adding i to the subset and setting pq[i] = key and the call pq.changeKey(i, key) as setting pq[i] = key, both also maintaining data structures needed to support the other operations, most importantly delMin() (remove and return the index of the minimum key) and changeKey() (change the item associated with an index that is already in the data structure—just as in pq[i] = key). These operations are important in many applications and are enabled by our ability to refer to the key (with the index). EXERCISE 2.4.33 describes how to extend ALGORITHM 2.6 to implement index priority queues with remarkable efficiency and with remarkably little code. Intuitively, when an item in the heap changes, we can restore the heap invariant with a sink operation (if the key decreases) and a swim operation (if the key increases). To perform the operations, we use the index to find the item in the heap. The ability to locate an item in the heap also allows us to add the delete() operation to the API.
Proposition Q (continued). In an index priority queue of size N, the number of compares required is proportional to at most log N for insert, change priority, delete, and remove the minimum.
Proof: Immediate from inspection of the code and the fact that all paths in a heap are of length at most ~lg N.
This discussion is for a minimum-oriented queue; as usual, we also implement on the booksite a maximum-oriented version IndexMaxPQ.
Index priority-queue client
The IndexMinPQ client Multiway on page 322 solves the multiway merge problem: it merges together several sorted input streams into one sorted output stream. This problem arises in many applications: the streams might be the output of scientific instruments (sorted by time), lists of information from the web such as music or movies (sorted by title or artist name), commercial transactions (sorted by account number or time), or whatever. If you have the space, you might just read them all into an array and sort them, but with a priority queue, you can read input streams and put them in sorted order on the output no matter how long they are.
Multiway merge priority-queue client
public class Multiway
{
public static void merge(In[] streams)
{
int N = streams.length;
IndexMinPQ<String> pq = new IndexMinPQ<String>(N);
for (int i = 0; i < N; i++)
if (!streams[i].isEmpty())
pq.insert(i, streams[i].readString());
while (!pq.isEmpty())
{
StdOut.println(pq.minKey());
int i = pq.delMin();
if (!streams[i].isEmpty())
pq.insert(i, streams[i].readString());
}
}
public static void main(String[] args)
{
int N = args.length;
In[] streams = new In[N];
for (int i = 0; i < N; i++)
streams[i] = new In(args[i]);
merge(streams);
}
}
This IndexMinPQ client merges together the sorted input streams given as command-line arguments into a single sorted output stream on standard output (see text). Each stream index is associated with a key (the next string in the stream). After initialization, it enters a loop that prints the smallest string in the queue and removes the corresponding entry, then adds a new entry for the next string in that stream. For economy, the output is shown on one line below—the actual output is one string per line.
Heapsort
We can use any priority queue to develop a sorting method. We insert all the items to be sorted into a minimum-oriented priority queue, then repeatedly use remove the minimum to remove them all in order. Using a priority queue represented as an unordered array in this way corresponds to doing a selection sort; using an ordered array corresponds to doing an insertion sort. What sorting method do we get if we use a heap? An entirely different one! Next, we use the heap to develop a classic elegant sorting algorithm known as heapsort.
Heapsort breaks into two phases: heap construction, where we reorganize the original array into a heap, and the sortdown, where we pull the items out of the heap in decreasing order to build the sorted result. For consistency with the code we have studied, we use a maximum-oriented priority queue and repeatedly remove the maximum. Focusing on the task of sorting, we abandon the notion of hiding the representation of the priority queue and use swim() and sink() directly. Doing so allows us to sort an array without needing any extra space, by maintaining the heap within the array to be sorted.
Heap construction
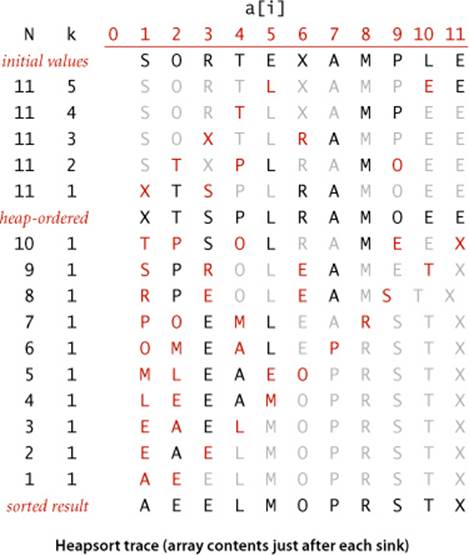
How difficult is the process of building a heap from N given items? Certainly we can accomplish this task in time proportional to N log N, by proceeding from left to right through the array, using swim() to ensure that the items to the left of the scanning pointer make up a heap-ordered complete tree, like successive priority-queue insertions. A clever method that is much more efficient is to proceed from right to left, using sink() to make subheaps as we go. Every position in the array is the root of a small subheap; sink() works for such subheaps, as well. If the two children of a node are heaps, then calling sink() on that node makes the subtree rooted at the parent a heap. This process establishes the heap order inductively. The scan starts halfway back through the array because we can skip the subheaps of size 1. The scan ends at position 1, when we finish building the heap with one call to sink(). As the first phase of a sort, heap construction is a bit counterintuitive, because its goal is to produce a heap-ordered result, which has the largest item first in the array (and other larger items near the beginning), not at the end, where it is destined to finish.
Proposition R. Sink-based heap construction uses fewer than 2N compares and fewer than N exchanges to construct a heap from N items.
Proof: This fact follows from the observation that most of the heaps processed are small. For example, to build a heap of 127 items, we process 32 heaps of size 3, 16 heaps of size 7, 8 heaps of size 15, 4 heaps of size 31, 2 heaps of size 63, and 1 heap of size 127, so 32·1 + 16·2 + 8·3 + 4·4 + 2·5 + 1·6 = 120 exchanges (twice as many compares) are required (at worst). See EXERCISE 2.4.20 for a complete proof.
Algorithm 2.7 Heapsort
public static void sort(Comparable[] a)
{
int N = a.length;
for (int k = N/2; k >= 1; k--)
sink(a, k, N);
while (N > 1)
{
exch(a, 1, N--);
sink(a, 1, N);
}
}
This code sorts a[1] through a[N] using the sink() method (modified to take a[] and N as arguments). The for loop constructs the heap; then the while loop exchanges the largest element a[1] with a[N] and then repairs the heap, continuing until the heap is empty. Decrementing the array indices in the implementations of exch() and less() gives an implementation that sorts a[0] througha[N-1], consistent with our other sorts.
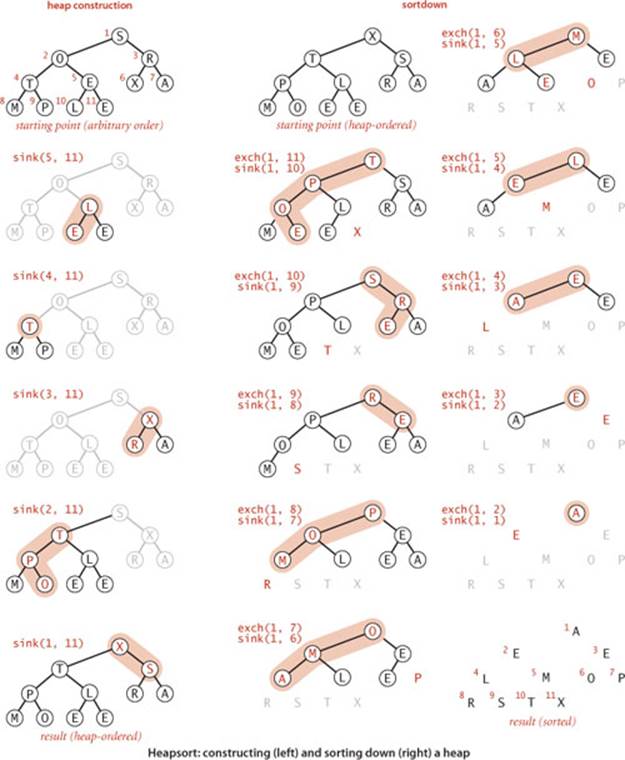
Sortdown
Most of the work during heapsort is done during the second phase, where we remove the largest remaining item from the heap and put it into the array position vacated as the heap shrinks. This process is a bit like selection sort (taking the items in decreasing order instead of in increasing order), but it uses many fewer compares because the heap provides a much more efficient way to find the largest item in the unsorted part of the array.
Proposition S. Heapsort uses fewer than 2N lg N + 2N compares (and half that many exchanges) to sort N items.
Proof: The 2 N term covers the cost of heap construction (see PROPOSITION R). The 2 N lg N term follows from bounding the cost of each sink operation during the sortdown by 2lg N (see PROPOSITION Q).
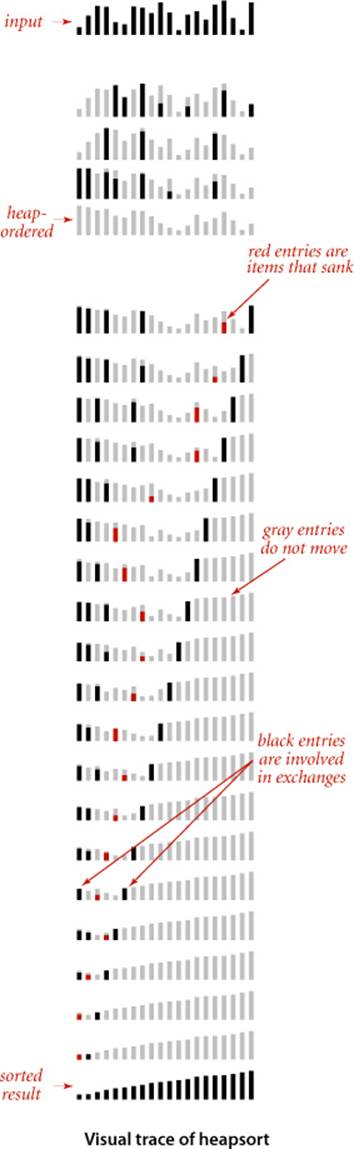
ALGORITHM 2.7 is a full implementation based on these ideas, the classical heapsort algorithm, which was invented by J. W. J. Williams and refined by R. W. Floyd in 1964. Although the loops in this program seem to do different tasks (the first constructs the heap, and the second destroys the heap for the sortdown), they are both built around the sink() method. We provide an implementation outside of our priority-queue API to highlight the simplicity of the sorting algorithm (eight lines of code for sort() and another eight lines of code for sink()) and to make it an in-place sort.
As usual, you can gain some insight into the operation of the algorithm by studying a visual trace. At first, the process seems to do anything but sort, because large items are moving to the beginning of the array as the heap is being constructed. But then the method looks more like a mirror image of selection sort (except that it uses far fewer compares).
As for all of the other methods that we have studied, various people have investigated ways to improve heap-based priority-queue implementations and heapsort. We now briefly consider one of them.
Sink to the bottom, then swim
Most items reinserted into the heap during sortdown go all the way to the bottom. Floyd observed in 1964 that we can thus save time by avoiding the check for whether the item has reached its position, simply promoting the larger of the two children until the bottom is reached, then moving back up the heap to the proper position. This idea cuts the number of compares by a factor of 2 asymptotically—close to the number used by mergesort (for a randomly-ordered array). The method requires extra bookkeeping, and it is useful in practice only when the cost of compares is relatively high (for example, when we are sorting items with strings or other types of long keys).
HEAPSORT IS SIGNIFICANT in the study of the complexity of sorting (see page 279) because it is the only method that we have seen that is optimal (within a constant factor) in its use of both time and space—it is guaranteed to use ~2N lg N compares and constant extra space in the worst case. When space is very tight (for example, in an embedded system or on a low-cost mobile device) it is popular because it can be implemented with just a few dozen lines (even in machine code) while still providing optimal performance. However, it is rarely used in typical applications on modern systems because it has poor cache performance: array entries are rarely compared with nearby array entries, so the number of cache misses is far higher than for quicksort, mergesort, and even shellsort, where most compares are with nearby entries.
On the other hand, the use of heaps to implement priority queues plays an increasingly important role in modern applications, because it provides an easy way to guarantee logarithmic running time for dynamic situations where large numbers of insert and remove the maximum operations are intermixed. We will encounter several examples later in this book.
Q&A
Q. I’m still not clear on the purpose of priority queues. Why exactly don’t we just sort and then consider the items in increasing order in the sorted array?
A. In some data-processing examples such as TopM and Multiway, the total amount of data is far too large to consider sorting (or even storing in memory). If you are looking for the top ten entries among a billion items, do you really want to sort a billion-entry array? With a priority queue, you can do it with a ten-entry priority queue. In other examples, all the data does not even exist together at any point in time: we take something from the priority queue, process it, and as a result of processing it perhaps add some more things to the priority queue.
Q. Why not use Comparable, as we do for sorts, instead of the generic Item in MaxPQ?
A. Doing so would require the client to cast the return value of delMax() to an actual type, such as String. Generally, casts in client code are to be avoided.
Q. Why not use a[0] in the heap representation?
A. Doing so simplifies the arithmetic a bit. It is not difficult to implement the heap methods based on a 0-based heap where the children of a[0] are a[1] and a[2], the children of a[1] are a[3] and a[4], the children of a[2] are a[5] and a[6], and so forth, but most programmers prefer the simpler arithmetic that we use. Also, using a[0] as a sentinel value (in the parent of a[1]) is useful in some heap applications.
Q. Building a heap in heapsort by inserting items one by one seems simpler to me than the tricky bottom-up method described on page 323 in the text. Why bother?
A. For a sort implementation, it is 20 percent faster and requires half as much tricky code (no swim() needed). The difficulty of understanding an algorithm has not necessarily much to do with its simplicity, or its efficiency.
Q. What happens if I leave off the extends Comparable<Key> phrase in an implementation like MaxPQ ?
A. As usual, the easiest way for you to answer a question of this sort for yourself is to simply try it. If you do so for MaxPQ you will get a compile-time error:
MaxPQ.java:21: cannot find symbol
symbol : method compareTo(Key)
which is Java’s way of telling you that it does not know about compareTo() in Item because you neglected to declare that key extends Comparable<Item>.
Exercises
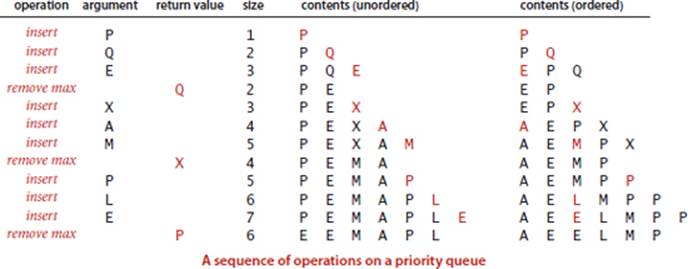
2.4.1 Suppose that the sequence P R I O * R * * I * T * Y * * * Q U E * * * U * E (where a letter means insert and an asterisk means remove the maximum) is applied to an initially empty priority queue. Give the sequence of letters returned by the remove the maximum operations.
2.4.2 Criticize the following idea: To implement find the maximum in constant time, why not use a stack or a queue, but keep track of the maximum value inserted so far, then return that value for find the maximum?
2.4.3 Provide priority-queue implementations that support insert and remove the maximum, one for each of the following underlying data structures: unordered array, ordered array, unordered linked list, and ordered linked list. Give a table of the worst-case bounds for each operation for each of your four implementations.
2.4.4 Is an array that is sorted in decreasing order a max-oriented heap?
2.4.5 Give the heap that results when the keys E A S Y Q U E S T I O N are inserted in that order into an initially empty max-oriented heap.
2.4.6 Using the conventions of EXERCISE 2.4.1, give the sequence of heaps produced when the operations P R I O * R * * I * T * Y * * * Q U E * * * U * E are performed on an initially empty max-oriented heap.
2.4.7 The largest item in a heap must appear in position 1, and the second largest must be in position 2 or position 3. Give the list of positions in a heap of size 31 where the kth largest (i) can appear, and (ii) cannot appear, for k=2, 3, 4 (assuming the values to be distinct).
2.4.8 Answer the previous exercise for the kth smallest item.
2.4.9 Draw all of the different heaps that can be made from the five keys A B C D E, then draw all of the different heaps that can be made from the five keys A A A B B.
2.4.10 Suppose that we wish to avoid wasting one position in a heap-ordered array pq[], putting the largest value in pq[0], its children in pq[1] and pq[2], and so forth, proceeding in level order. Where are the parents and children of pq[k]?
2.4.11 Suppose that your application will have a huge number of insert operations, but only a few remove the maximum operations. Which priority-queue implementation do you think would be most effective: heap, unordered array, or ordered array?
2.4.12 Suppose that your application will have a huge number of find the maximum operations, but a relatively small number of insert and remove the maximum operations. Which priority-queue implementation do you think would be most effective: heap, unordered array, or ordered array?
2.4.13 Describe a way to avoid the j < N test in sink().
2.4.14 What is the minimum number of items that must be exchanged during a remove the maximum operation in a heap of size N with no duplicate keys? Give a heap of size 15 for which the minimum is achieved. Answer the same questions for two and three successive remove the maximumoperations.
2.4.15 Design a linear-time certification algorithm to check whether an array pq[] is a min-oriented heap.
2.4.16 For N=32, give arrays of items that make heapsort use as many and as few compares as possible.
2.4.17 Prove that building a minimum-oriented priority queue of size k then doing N − k replace the minimum (insert followed by remove the minimum) operations leaves the k largest of the N items in the priority queue.
2.4.18 In MaxPQ, suppose that a client calls insert() with an item that is larger than all items in the queue, and then immediately calls delMax(). Assume that there are no duplicate keys. Is the resulting heap identical to the heap as it was before these operations? Answer the same question for twoinsert() operations (the first with a key larger than all keys in the queue and the second for a key larger than that one) followed by two delMax() operations.
2.4.19 Implement the constructor for MaxPQ that takes an array of items as argument, using the bottom-up heap construction method described on page 323 in the text.
2.4.20 Prove that sink-based heap construction uses fewer than 2N compares and fewer than N exchanges.
Creative Problems
2.4.21 Elementary data structures. Explain how to use a priority queue to implement the stack, queue, and randomized queue data types from SECTION 1.3. and EXERCISE 1.3.35.
2.4.22 Array resizing. Add array resizing to MaxPQ, and prove bounds like those of PROPOSITION Q for array accesses, in an amortized sense.
2.4.23 Multiway heaps. Considering the cost of compares only, and assuming that it takes t compares to find the largest of t items, find the value of t that minimizes the coefficient of Nlg N in the compare count when a t-ary heap is used in heapsort. First, assume a straightforward generalization of sink(); then, assume that Floyd’s method can save one compare in the inner loop.
2.4.24 Priority queue with explicit links. Implement a priority queue using a heap-ordered binary tree, but use a triply linked structure instead of an array. You will need three links per node: two to traverse down the tree and one to traverse up the tree. Your implementation should guarantee logarithmic running time per operation, even if no maximum priority-queue size is known ahead of time.
2.4.25 Computational number theory. Write a program that prints out all integers of the form a3 + b3 where a and b are integers between 0 and N in sorted order, without using excessive space. That is, instead of computing an array of the N2 sums and sorting them, build a minimum-oriented priority queue, initially containing (03, 0, 0), (13, 1, 0), (23, 2, 0), . . ., (N3, N, 0). Then, while the priority queue is nonempty, remove the smallest item (i3 + j3, i, j), print it, and then, if j < N, insert the item (i3 + (j+1)3, i, j+1). Use this program to find all distinct integers a, b, c, and d between 0 and 106 such that a3 + b3 = c3 + d3.
2.4.26 Heap without exchanges. Because the exch() primitive is used in the sink() and swim() operations, the items are loaded and stored twice as often as necessary. Give more efficient implementations that avoid this inefficiency, a la insertion sort (see EXERCISE 2.1.25).
2.4.27 Find the minimum. Add a min() method to MaxPQ. Your implementation should use constant time and constant extra space.
2.4.28 Selection filter. Write a program similar to TopM that reads points (x, y, z) from standard input, takes a value M from the command line, and prints the M points that are closest to the origin in Euclidean distance. Estimate the running time of your client for N = 108 and M = 104.
2.4.29 Min/max priority queue. Design a data type that supports the following operations: insert, delete the maximum, and delete the minimum (all in logarithmic time); and find the maximum and find the minimum (both in constant time). Hint: Use two heaps.
2.4.30 Dynamic median-finding. Design a data type that supports insert in logarithmic time, find the median in constant time, and delete the median in logarithmic time. Hint: Use a min-heap and a max-heap.
2.4.31 Fast insert. Develop a compare-based implementation of the MinPQ API such that insert uses ~ log log N compares and delete the minimum uses ~2 log N compares. Hint: Use binary search on parent pointers to find the ancestor in swim().
2.4.32 Lower bound. Prove that it is impossible to develop a compare-based implementation of the MinPQ API such that both insert and delete the minimum guarantee to use ~ log log N compares per operation
2.4.33 Index priority-queue implementation. Implement the basic operations in the index priority-queue API on page 320 by modifying ALGORITHM 2.6 as follows: Change pq[] to hold indices, add an array keys[] to hold the key values, and add an array qp[] that is the inverse of pq[] — qp[i] gives the position of i in pq[] (the index j such that pq[j] is i). Then modify the code in ALGORITHM 2.6 to maintain these data structures. Use the convention that qp[i] = -1 if i is not on the queue, and include a method contains() that tests this condition. You need to modify the helper methods exch() andless() but not sink() or swim().
Partial solution:
public class IndexMinPQ<Key extends Comparable<Key>>
{
private int N; // number of elements on PQ
private int[] pq; // binary heap using 1-based indexing
private int[] qp; // inverse: qp[pq[i]] = pq[qp[i]] = i
private Key[] keys; // items with priorities
public IndexMinPQ(int maxN)
{
keys = (Key[]) new Comparable[maxN + 1];
pq = new int[maxN + 1];
qp = new int[maxN + 1];
for (int i = 0; i <= maxN; i++) qp[i] = -1;
}
public boolean isEmpty()
{ return N == 0; }
public boolean contains(int i)
{ return qp[i] != -1; }
public void insert(int k, Key key)
{
N++;
qp[i] = N;
pq[i] = k;
keys[i] = key;
swim(N);
}
public Key minKey()
{ return keys[pq[1]]; }
public int delMin()
{
int indexOfMin = pq[1];
exch(1, N--);
sink(1);
keys[pq[N+1]] = null;
qp[pq[N+1]] = -1;
return indexOfMin;
}
2.4.34 Index priority-queue implementation (additional operations). Add minIndex(), change(), and delete() to your implementation of EXERCISE 2.4.33.
Solution:
public int minIndex()
{ return pq[1]; }
public void changeKey(int i, Key key)
{
keys[i] = key;
swim(qp[i]);
sink(qp[i]);
}
public void delete(int i)
{
int index = qp[i];
exch(index, N--);
swim(index);
sink(index);
keys[i] = null;
qp[i] = -1;
}
2.4.35 Sampling from a discrete probability distribution. Write a class Sample with a constructor that takes an array p[] of double values as argument and supports the following two operations: random()—return an index i with probability p[i]/T (where T is the sum of the numbers in p[])—and change(i, v)—change the value of p[i] to v. Hint: Use a complete binary tree where each node has implied weight p[i]. Store in each node the cumulative weight of all the nodes in its subtree. To generate a random index, pick a random number between 0 and T and use the cumulative weights to determine which branch of the subtree to explore. When updating p[i], change all of the weights of the nodes on the path from the root to i. Avoid explicit pointers, as we do for heaps.
Experiments
2.4.36 Performance driver I. Write a performance driver client program that uses insert to fill a priority queue, then uses remove the maximum to remove half the keys, then uses insert to fill it up again, then uses remove the maximum to remove all the keys, doing so multiple times on random sequences of keys of various lengths ranging from small to large; measures the time taken for each run; and prints out or plots the average running times.
2.4.37 Performance driver II. Write a performance driver client program that uses insert to fill a priority queue, then does as many remove the maximum and insert operations as it can do in 1 second, doing so multiple times on random sequences of keys of various lengths ranging from small to large; and prints out or plots the average number of remove the maximum operations it was able to do.
2.4.38 Exercise driver. Write an exercise driver client program that uses the methods in our priority-queue interface of ALGORITHM 2.6 on difficult or pathological cases that might turn up in practical applications. Simple examples include keys that are already in order, keys in reverse order, all keys the same, and sequences of keys having only two distinct values.
2.4.39 Cost of construction. Determine empirically the percentage of time heapsort spends in the construction phase for N = 103, 106, and 109.
2.4.40 Floyd’s method. Implement a version of heapsort based on Floyd’s sink-to-the-bottom-and-then-swim idea, as described in the text. Count the number of compares used by your program and the number of compares used by the standard implementation, for randomly ordered distinct keys with N = 103, 106, and 109.
2.4.41 Multiway heaps. Implement a version of heapsort based on complete heap-ordered 3-ary and 4-ary trees, as described in the text. Count the number of compares used by each and the number of compares used by the standard implementation, for randomly ordered distinct keys with N = 103, 106, and 109.
2.4.42 Preorder heaps. Implement a version of heapsort based on the idea of representing the heap-ordered tree in preorder rather than in level order. Count the number of compares used by your program and the number of compares used by the standard implementation, for randomly ordered keys with N = 103, 106, and 109.