Algorithms (2014)
Three. Searching
3.1 Symbol Tables 362
3.2 Binary Search Trees 396
3.3 Balanced Search Trees 424
3.4 Hash Tables 458
3.5 Applications 486
Modern computing and the internet have made accessible a vast amount of information. The ability to efficiently search through this information is fundamental to processing it. This chapter describes classical searching algorithms that have proven to be effective in numerous diverse applications for decades. Without algorithms like these, the development of the computational infrastructure that we enjoy in the modern world would not have been possible.
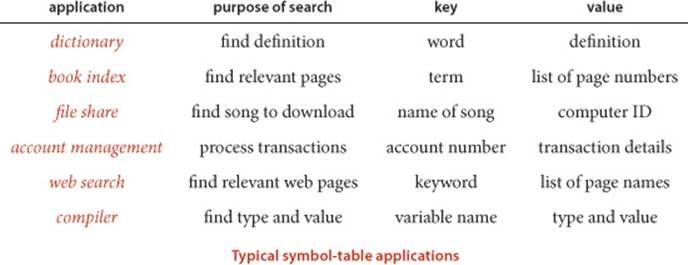
We use the term symbol table to describe an abstract mechanism where we save information (a value) that we can later search for and retrieve by specifying a key. The nature of the keys and the values depends upon the application. There can be a huge number of keys and a huge amount of information, so implementing an efficient symbol table is a significant computational challenge.
Symbol tables are sometimes called dictionaries, by analogy with the time-honored system of providing definitions for words by listing them alphabetically in a reference book. In an English-language dictionary, a key is a word and its value is the entry associated with the word that contains the definition, pronunciation, and etymology. Symbol tables are also sometimes called indices, by analogy with another time-honored system of providing access to terms by listing them alphabetically at the end of a book such as a textbook. In a book index, a key is a term of interest and its value is the list of page numbers that tell readers where to find that term in the book.
After describing the basic APIs and two fundamental implementations, we consider three classic data structures that can support efficient symbol-table implementations: binary search trees, red-black trees, and hash tables. We conclude with several extensions and applications, many of which would not be feasible without the efficient algorithms that you will learn about in this chapter.
3.1 Symbol Tables
The primary purpose of a symbol table is to associate a value with a key. The client can insert key-value pairs into the symbol table with the expectation of later being able to search for the value associated with a given key, from among all of the key-value pairs that have been put into the table. This chapter describes several ways to structure this data so as to make efficient not just the insert and search operations, but several other convenient operations as well. To implement a symbol table, we need to define an underlying data structure and then specify algorithms for insert, search, and other operations that create and manipulate the data structure.
Search is so important to so many computer applications that symbol tables are available as high-level abstractions in many programming environments, including Java—we shall discuss Java’s symbol-table implementations in SECTION 3.5. The table below gives some examples of keys and values that you might use in typical applications. We consider some illustrative reference clients soon, and SECTION 3.5 is devoted to showing you how to use symbol tables effectively in your own clients. We also use symbol tables in developing other algorithms throughout the book.
Definition. A symbol table is a data structure for key-value pairs that supports two operations: insert (put) a new pair into the table and search for (get) the value associated with a given key.
API
The symbol table is a prototypical abstract data type (see CHAPTER 1): it represents a well-defined set of values and operations on those values, enabling us to develop clients and implementations separately. As usual, we precisely define the operations by specifying an applications programming interface (API) that provides the contract between client and implementation:

Before examining client code, we consider several design choices for our implementations to make our code consistent, compact, and useful.
Generics
As we did with sorting, we will consider the methods without specifying the types of the items being processed, using generics. For symbol tables, we emphasize the separate roles played by keys and values in search by specifying the key and value types explicitly instead of viewing keys as implicit in items as we did for priority queues in SECTION 2.4. After we have considered some of the characteristics of this basic API (for example, note that there is no mention of order among the keys), we will consider an extension for the typical case when keys are Comparable, which enables numerous additional methods.
Duplicate keys
We adopt the following conventions in all of our implementations:
• Only one value is associated with each key (no duplicate keys in a table).
• When a client puts a key-value pair into a table already containing that key (and an associated value), the new value replaces the old one.
These conventions define the associative array abstraction, where you can think of a symbol table as being just like an array, where keys are indices and values are array entries. In a conventional array, keys are integer indices that we use to quickly access array values; in an associative array (symbol table), keys are of arbitrary type, but we can still use them to quickly access values. Some programming languages (not Java) provide special support that allows programmers to use code such as st[key] for st.get(key) and st[key] = val for st.put(key, val) where key and val are objects of arbitrary type.
Null keys
Keys must not be null. As with many mechanisms in Java, use of a null key results in an exception at runtime (see the third Q&A on page 387).
Null values
We also adopt the convention that no key can be associated with the value null. This convention is directly tied to our specification in the API that get() should return null for keys not in the table, effectively associating the value null with every key not in the table. This convention has two (intended) consequences: First, we can test whether or not the symbol table defines a value associated with a given key by testing whether get() returns null. Second, we can use the operation of calling put() with null as its second (value) argument to implement deletion, as described in the next paragraph.
Deletion
Deletion in symbol tables generally involves one of two strategies: lazy deletion, where we associate keys in the table with null, then perhaps remove all such keys at some later time; and eager deletion, where we remove the key from the table immediately. As just discussed, the code put(key, null) is an easy (lazy) implementation of delete(key). When we give an (eager) implementation of delete(), it is intended to replace this default. In our symbol-table implementations that do not use the default delete(), the put() implementations on the booksite begin with the defensive code
if (val == null) { delete(key); return; }
to ensure that no key in the table is associated with null. For economy, we do not include this code in the book (and we do not call put() with a null value in client code).
Shorthand methods
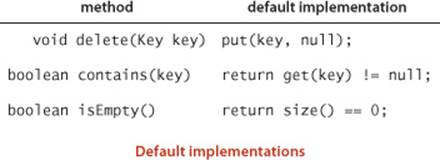
For clarity in client code, we include the methods contains() and isEmpty() in the API, with the default one-line implementations shown here. For economy, we do not repeat this code, but we assume it to be present in all implementations of the symbol-table API and use these methods freely in client code.
Iteration
To enable clients to process all the keys and values in the table, we might add the phrase implements Iterable<Key> to the first line of the API to specify that every implementation must implement an iterator() method that returns an iterator having appropriate implementations of hasNext() and next(), as described for stacks and queues in SECTION 1.3. For symbol tables, we adopt a simpler alternative approach, where we specify a keys() method that returns an Iterable<Key> object for clients to use to iterate through the keys. Our reason for doing so is to maintain consistency with methods that we will define for ordered symbol tables that allow clients to iterate through a specified subset of keys in the table.
Key equality
Determining whether or not a given key is in a symbol table is based on the concept of object equality, which we discussed at length in SECTION 1.2 (see page 102). Java’s convention that all objects inherit an equals() method and its implementation of equals() both for standard types such asInteger, Double, and String and for more complicated types such as File and URL is a head start—when using these types of data, you can just use the built-in implementation. For example, if x and y are String values, then x.equals(y) is true if and only if x and y have the same length and are identical in each character position. For such client-defined keys, you need to override equals(), as discussed in SECTION 1.2. You can use our implementation of equals() for Date (page 103) as a template to develop equals() for a type of your own. As discussed for priority queues on page 320, a best practice is to make Key types immutable, because consistency cannot otherwise be guaranteed.
Ordered symbol tables
In typical applications, keys are Comparable objects, so the option exists of using the code a.compareTo(b) to compare two keys a and b. Several symbol-table implementations take advantage of order among the keys that is implied by Comparable to provide efficient implementations of the put() and get()operations. More important, in such implementations, we can think of the symbol table as keeping the keys in order and consider a significantly expanded API that defines numerous natural and useful operations involving relative key order. For example, suppose that your keys are times of the day. You might be interested in knowing the earliest or the latest time, the set of keys that fall between two given times, and so forth. In most cases, such operations are not difficult to implement with the same data structures and methods underlying the put() and get() implementations. Specifically, for applications where keys are Comparable, we implement in this chapter the following API:

Your signal that one of our programs is implementing this API is the presence of the Key extends Comparable<Key> generic type variable in the class declaration, which specifies that the code depends upon the keys being Comparable and implements the richer set of operations. Together, these operations define for client programs an ordered symbol table.
Minimum and maximum
Perhaps the most natural queries for a set of ordered keys are to ask for the smallest and largest keys. We have already encountered these operations, in our discussion of priority queues in SECTION 2.4. In ordered symbol tables, we also have methods to delete the maximum and minimum keys (and their associated values). With this capability, the symbol table can operate like the IndexMinPQ() class that we discussed in SECTION 2.4. The primary differences are that equal keys are allowed in priority queues but not in symbol tables and that ordered symbol tables support a much larger set of operations.
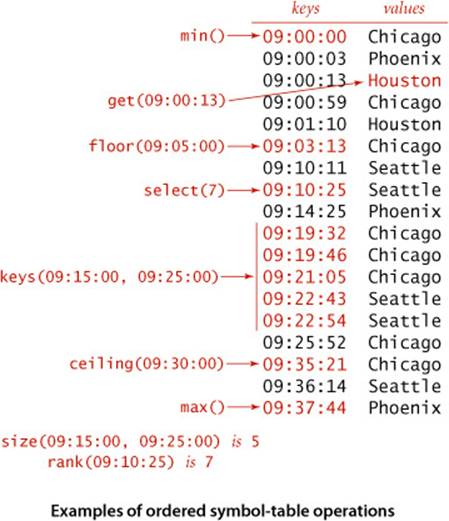
Floor and ceiling
Given a key, it is often useful to be able to perform the floor operation (find the largest key that is less than or equal to the given key) and the ceiling operation (find the smallest key that is greater than or equal to the given key). The nomenclature comes from functions defined on real numbers (the floor of a real number x is the largest integer that is smaller than or equal to x and the ceiling of a real number x is the smallest integer that is greater than or equal to x).
Rank and selection
The basic operations for determining where a new key fits in the order are the rank operation (find the number of keys less than a given key) and the select operation (find the key with a given rank). To test your understanding of their meaning, confirm for yourself that both i == rank(select(i))for all i between 0 and size()-1 and all keys in the table satisfy key == select(rank(key)). We have already encountered the need for these operations, in our discussion of sort applications in SECTION 2.5. For symbol tables, our challenge is to perform these operations quickly, intermixed with insertions, deletions, and searches.
Range queries
How many keys fall within a given range (between two given keys)? Which keys fall in a given range? The two-argument size() and keys() methods that answer these questions are useful in many applications, particularly in large databases. The capability to handle such queries is one prime reason that ordered symbol tables are so widely used in practice.
Exceptional cases
When a method is to return a key and there is no key fitting the description in the table, our convention is to throw an exception (an alternate approach, which is also reasonable, would be to return null in such cases). For example, min(), max(), deleteMin(), deleteMax(), floor(), and ceiling() all throw exceptions if the table is empty, as does select(k) if k is less than 0 or not less than size().
Shorthand methods
As we have already seen with isEmpty() and contains() in our basic API, we keep some redundant methods in the API for clarity in client code. For economy in the text, we assume that the following default implementations are included in any implementation of the ordered symbol-table API unless otherwise specified:

Key equality (revisited)
The best practice in Java is to make compareTo() consistent with equals() in all Comparable types. That is, for every pair of values a and b in any given Comparable type, it should be the case that (a.compareTo(b) == 0) and a.equals(b) have the same value. To avoid any potential ambiguities, we avoid the use ofequals() in ordered symbol-table implementations. Instead, we use compareTo() exclusively to compare keys: we take the boolean expression a.compareTo(b) == 0 to mean “Are a and b equal?” Typically, such a test marks the successful end of a search for a in the symbol table (by finding b). As you saw with sorting algorithms, Java provides standard implementations of compareTo() for many commonly used types of keys, and it is not difficult to develop a compareTo() implementation for your own data types (see SECTION 2.5).
Cost model
Whether we use equals() (for symbol tables where keys are not Comparable) or compareTo() (for ordered symbol tables with Comparable keys), we use the term compare to refer to the operation of comparing a symbol-table entry against a search key. In most symbol-table implementations, this operation is in the inner loop. In the few cases where that is not the case, we also count array accesses.
Searching cost model. When studying symbol-table implementations, we count compares (equality tests or key comparisons). In (rare) cases where compares are not in the inner loop, we count array accesses.
SYMBOL-TABLE IMPLEMENTATIONS are generally characterized by their underlying data structures and their implementations of get() and put(). We do not always provide implementations of all of the other methods in the text because many of them make good exercises to test your understanding of the underlying data structures. To distinguish implementations, we add a descriptive prefix to ST that refers to the implementation in the class name of symbol-table implementations. In clients, we use ST to call on a reference implementation unless we wish to refer to a specific implementation. You will gradually develop a better feeling for the rationale behind the methods in the APIs in the context of the numerous clients and symbol-table implementations that we present and discuss throughout this chapter and throughout the rest of this book. We also discuss alternatives to the various design choices that we have described here in the Q&A and exercises.
Sample clients
While we defer detailed consideration of applications to SECTION 3.5, it is worthwhile to consider some client code before considering implementations. Accordingly, we now consider two clients: a test client that we use to trace algorithm behavior on small inputs and a performance client that we use to motivate the development of efficient implementations.
Test client
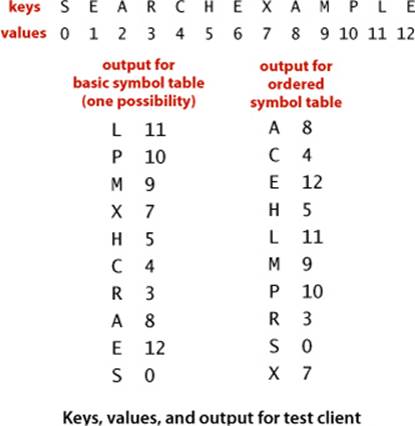
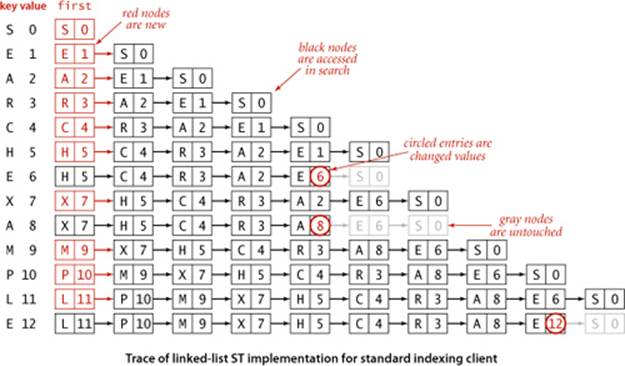
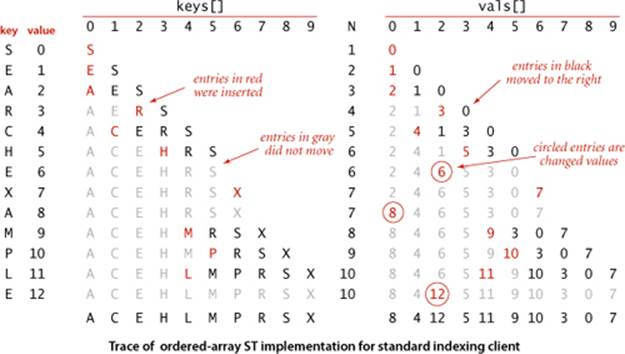
For tracing our algorithms on small inputs we assume that all of our implementations use the test client below, which takes a sequence of strings from standard input, builds a symbol table that associates the value i with the ith string in the input, and then prints the table. In the traces in the text, we assume that the input is a sequence of single-character strings. Most often, we use the string "S E A R C H E X A M P L E". By our conventions, this client associates the key S with the value 0, the key R with the value 3, and so forth. But E is associated with the value 12 (not 1 or 6) and A with the value 8 (not 2) because our associative-array convention implies that each key is associated with the value used in the most recent call to put(). For basic (unordered) implementations, the order of the keys in the output of this test client is not specified (it depends on characteristics of the implementation); for an ordered symbol table the test client prints the keys in sorted order. This client is an example of an indexing client, a special case of a fundamental symbol-table application that we discuss in SECTION 3.5.
Basic symbol-table test client
public static void main(String[] args)
{
ST<String, Integer> st;
st = new ST<String, Integer>();
for (int i = 0; !StdIn.isEmpty(); i++)
{
String key = StdIn.readString();
st.put(key, i);
}
for (String s : st.keys())
StdOut.println(s + " " + st.get(s));
}
Performance client
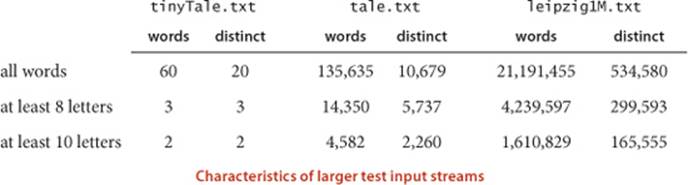
FrequencyCounter (on the next page) is a symbol-table client that finds the number of occurrences of each string (having at least as many characters as a given threshold length) in a sequence of strings from standard input, then iterates through the keys to find the one that occurs the most frequently. This client is an example of a dictionary client, an application that we discuss in more detail in SECTION 3.5. This client answers a simple question: Which word (no shorter than a given length) occurs most frequently in a given text? Throughout this chapter, we measure performance of this client with three reference inputs: the first five lines of C. Dickens’s Tale of Two Cities (tinyTale.txt), the full text of the book (tale.txt), and a popular database of 1 million sentences taken at random from the web that is known as the Leipzig Corpora Collection (leipzig1M.txt). For example, here is the content of tinyTale.txt:
Small test input
% more tinyTale.txt
it was the best of times it was the worst of times
it was the age of wisdom it was the age of foolishness
it was the epoch of belief it was the epoch of incredulity
it was the season of light it was the season of darkness
it was the spring of hope it was the winter of despair
This text has 60 words taken from 20 distinct words, four of which occur ten times (the highest frequency). Given this input, FrequencyCounter will print out any of it, was, the, or of (the one chosen may vary, depending upon characteristics of the symbol-table implementation), followed by the frequency, 10.
To study performance for the larger inputs, it is clear that two measures are of interest: Each word in the input is used as a search key once, so the total number of words in the text is certainly relevant. Second, each distinct word in the input is put into the symbol table (and the total number of distinct words in the input gives the size of the table after all keys have been inserted), so the total number of distinct words in the input stream is certainly relevant. We need to know both of these quantities in order to estimate the running time of FrequencyCounter (for a start, see EXERCISE 3.1.6). We defer details until we consider some algorithms, but you should have in mind a general idea of the needs of typical applications like this one. For example, running FrequencyCounter on leipzig1M.txt for words of length 8 or more involves millions of searches in a table with hundreds of thousands of keys and values. A server on the web might need to handle billions of transactions on tables with millions of keys and values.
A symbol-table client
public class FrequencyCounter
{
public static void main(String[] args)
{
int minlen = Integer.parseInt(args[0]); // key-length cutoff
ST<String, Integer> st = new ST<String, Integer>();
while (!StdIn.isEmpty())
{ // Build symbol table and count frequencies.
String word = StdIn.readString();
if (word.length() < minlen) continue; // Ignore short keys.
if (!st.contains(word)) st.put(word, 1);
else st.put(word, st.get(word) + 1);
}
// Find a key with the highest frequency count.
String max = "";
st.put(max, 0);
for (String word : st.keys())
if (st.get(word) > st.get(max))
max = word;
StdOut.println(max + " " + st.get(max));
}
}
This ST client counts the frequency of occurrence of the strings in standard input, then prints out one that occurs with highest frequency. The command-line argument specifies a lower bound on the length of keys considered.
% java FrequencyCounter 1 < tinyTale.txt
it 10
% java FrequencyCounter 8 < tale.txt
business 122
% java FrequencyCounter 10 < leipzig1M.txt
government 24763
THE BASIC QUESTION THAT THIS CLIENT and these examples raise is the following: Can we develop a symbol-table implementation that can handle a huge number of get() operations on a large table, which itself was built with a large number of intermixed get() and put() operations? If you are only doing a few searches, any implementation will do, but you cannot make use of a client like FrequencyCounter for large problems without a good symbol-table implementation. FrequencyCounter is surrogate for a very common situation. Specifically, it has the following characteristics, which are shared by many other symbol-table clients:
• Search and insert operations are intermixed.
• The number of distinct keys is not small.
• Substantially more searches than inserts are likely.
• Search and insert patterns, though unpredictable, are not random.
Our goal is to develop symbol-table implementations that make it feasible to use such clients to solve typical practical problems.
Next, we consider two elementary implementations and their performance for FrequencyCounter. Then, in the next several sections, you will learn classic implementations that can achieve excellent performance for such clients, even for huge input streams and tables.
Sequential search in an unordered linked list
One straightforward option for the underlying data structure for a symbol table is a linked list of nodes that contain keys and values, as in the code on the facing page. To implement get(), we scan through the list, using equals() to compare the search key with the key in each node in the list. If we find the match, we return the associated value; if not, we return null. To implement put(), we also scan through the list, using equals() to compare the client key with the key in each node in the list. If we find the match, we update the value associated with that key to be the value given in the second argument; if not, we create a new node with the given key and value and insert it at the beginning of the list. This method is known as sequential search: we search by considering the keys in the table one after another, using equals() to test for a match with our search key.
ALGORITHM 3.1 (SequentialSearchST) is an implementation of our basic symbol-table API that uses standard list-processing mechanisms, which we have used for elementary data structures in CHAPTER 1. We have left the implementations of size(), keys(), and eager delete() for exercises. You are encouraged to work these exercises to cement your understanding of the linked-list data structure and the basic symbol-table API.
Can this linked-list-based implementation handle applications that need large tables, such as our sample clients? As we have noted, analyzing symbol-table algorithms is more complicated than analyzing sorting algorithms because of the difficulty of characterizing the sequence of operations that might be invoked by a given client. As noted for FrequencyCounter, the most common situation is that, while search and insert patterns are unpredictable, they certainly are not random. For this reason, we pay careful attention to worst-case performance. For economy, we use the term search hit to refer to a successful search and search miss to refer to an unsuccessful search.
Algorithm 3.1 Sequential search (in an unordered linked list)
public class SequentialSearchST<Key, Value>
{
private Node first; // first node in the linked list
private class Node
{ // linked-list node
Key key;
Value val;
Node next;
public Node(Key key, Value val, Node next)
{
this.key = key;
this.val = val;
this.next = next;
}
}
public Value get(Key key)
{ // Search for key, return associated value.
for (Node x = first; x != null; x = x.next)
if (key.equals(x.key))
return x.val; // search hit
return null; // search miss
}
public void put(Key key, Value val)
{ // Search for key. Update value if found; grow table if new.
for (Node x = first; x != null; x = x.next)
if (key.equals(x.key))
{ x.val = val; return; } // Search hit: update val.
first = new Node(key, val, first); // Search miss: add new node.
}
}
This ST implementation uses a private Node inner class to keep the keys and values in an unordered linked list. The get() implementation searches the list sequentially to find whether the key is in the table (and returns the associated value if so). The put() implementation also searches the list sequentially to check whether the key is in the table. If so, it updates the associated value; if not, it creates a new node with the given key and value and inserts it at the beginning of the list. Implementations of size(), keys(), and eager delete() are left for exercises.
Proposition A. Search misses and insertions in an (unordered) linked-list symbol table having N key-value pairs both require N compares, and search hits N compares in the worst case.
Proof: When searching for a key that is not in the list, we test every key in the table against the search key. Because of our policy of disallowing duplicate keys, we need to do such a search before each insertion.
Corollary. Inserting N distinct keys into an initially empty linked-list symbol table uses ~N2/2 compares.
It is true that searches for keys that are in the table need not take linear time. One useful measure is to compute the total cost of searching for all of the keys in the table, divided by N. This quantity is precisely the expected number of compares required for a search under the condition that searches for each key in the table are equally likely. We refer to such a search as a random search hit. Though client search patterns are not likely to be random, they often are well-described by this model. It is easy to show that the average number of compares for a random search hit is ~N/2: the get() method in ALGORITHM 3.1 uses 1 compare to find the first key, 2 compares to find the second key, and so forth, for an average cost of (1 + 2 + ... + N)/N = (N + 1)/2 ~ N/2.
This analysis strongly indicates that a linked-list implementation with sequential search is too slow for it to be used to solve huge problems such as our reference inputs with clients like FrequencyCounter. The total number of compares is proportional to the product of the number of searches and the number of inserts, which is more than 109 for Tale of Two Cities and more than 1014 for the Leipzig Corpora.
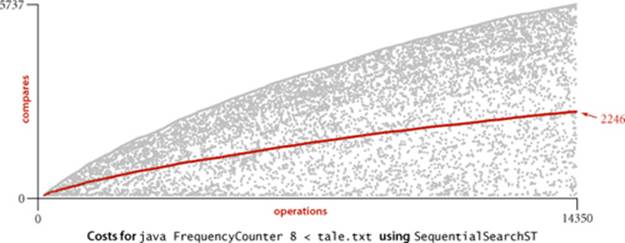
As usual, to validate analytic results, we need to run experiments. As an example, we study the operation of FrequencyCounter with command-line argument 8 for tale.txt, which involves 14,350 put() operations (recall that every word in the input leads to a put(), to update its frequency, and we ignore the cost of easily avoided calls to contains()). The symbol table grows to 5,737 keys, so about one-third of the operations increase the size of the table; the rest are searches. To visualize the performance, we use VisualAccumulator (see page 95) to plot two points corresponding to each put()operation as follows: for the ith put() operation we plot a gray point with x coordinate i and y coordinate the number of key compares it uses and a red point with x coordinate i and y coordinate the cumulative average number of key compares used for the first i put() operations. As with any scientific data, there is a great deal of information in this data for us to investigate (this plot has 14,350 gray points and 14,350 red points). In this context, our primary interest is that the plot validates our hypothesis that about half the list is accessed for the average put() operation. The actual total is slightly lower than half, but this fact (and the precise shape of the curves) is perhaps best explained by characteristics of the application, not our algorithms (see EXERCISE 3.1.36).
While detailed characterization of performance for particular clients can be complicated, specific hypotheses are easy to formulate and to test for FrequencyCounter with our reference inputs or with randomly ordered inputs, using a client like the DoublingTest client that we introduced in CHAPTER 1. We will reserve such testing for exercises and for the more sophisticated implementations that follow. If you are not already convinced that we need faster implementations, be sure to work these exercises (or just run FrequencyCounter with SequentialSearchST on leipzig1M.txt!).
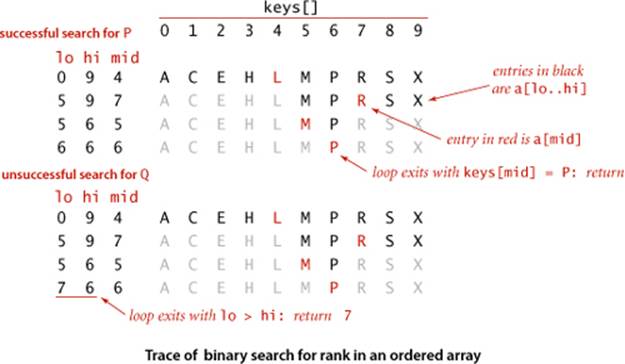
Binary search in an ordered array
Next, we consider a full implementation of our ordered symbol-table API. The underlying data structure is a pair of parallel arrays, one for the keys and one for the values. ALGORITHM 3.2 (BinarySearchST) on the facing page keeps Comparable keys in order in the array, then uses array indexing to enable fast implementation of get() and other operations.
The heart of the implementation is the rank() method, which returns the number of keys smaller than a given key. For get(), the rank tells us precisely where the key is to be found if it is in the table (and, if it is not there, that it is not in the table).
For put(), the rank tells us precisely where to update the value when the key is in the table, and precisely where to put the key when the key is not in the table. We move all larger keys over one position to make room (working from back to front) and insert the given key and value into the proper positions in their respective arrays. Again, studying BinarySearchST in conjunction with a trace of our test client is an instructive introduction to this data structure.
This code maintains parallel arrays of keys and values (see EXERCISE 3.1.12 for an alternative). As with our implementations of generic stacks and queues in CHAPTER 1, this code carries the inconvenience of having to create a Key array of type Comparable and a Value array of type Object, and to cast them back to Key[] and Value[] in the constructor. As usual, we can use array resizing so that clients do not have to be concerned with the size of the array (noting, as you shall see, that this method is too slow to use with large arrays).
Algorithm 3.2 Binary search (in an ordered array)
public class BinarySearchST<Key extends Comparable<Key>, Value>
{
private Key[] keys;
private Value[] vals;
private int N;
public BinarySearchST(int capacity)
{ // See Algorithm 1.1 for standard array-resizing code.
keys = (Key[]) new Comparable[capacity];
vals = (Value[]) new Object[capacity];
}
public int size()
{ return N; }
public Value get(Key key)
{
if (isEmpty()) return null;
int i = rank(key);
if (i < N && keys[i].compareTo(key) == 0) return vals[i];
else return null;
}
public int rank(Key key)
// See page 381.
public void put(Key key, Value val)
{ // Search for key. Update value if found; grow table if new.
int i = rank(key);
if (i < N && keys[i].compareTo(key) == 0)
{ vals[i] = val; return; }
for (int j = N; j > i; j--)
{ keys[j] = keys[j-1]; vals[j] = vals[j-1]; }
keys[i] = key; vals[i] = val;
N++;
}
public void delete(Key key)
// See Exercise 3.1.16 for this method.
}
This ST implementation keeps the keys and values in parallel arrays. The put() implementation moves larger keys one position to the right before growing the table as in the array-based stack implementation in SECTION 1.3. Array-resizing code is omitted here.
Binary search
The reason that we keep keys in an ordered array is so that we can use array indexing to dramatically reduce the number of compares required for each search, using the classic and venerable binary search algorithm that we used as an example in CHAPTER 1. We maintain indices into the sorted key array that delimit the subarray that might contain the search key. To search, we compare the search key against the key in the middle of the subarray. If the search key is less than the key in the middle, we search in the left half of the subarray; if the search key is greater than the key in the middle, we search in the right half of the subarray; otherwise the key in the middle is equal to the search key. The rank() code on the facing page uses binary search to complete the symbol-table implementation just discussed. This implementation is worthy of careful study. To study it, we start with the equivalent recursive code at left. A call to rank(key, 0, N-1) does the same sequence of compares as a call to the nonrecursive implementation in ALGORITHM 3.2, but this alternate version better exposes the structure of the algorithm, as discussed in SECTION 1.1. This recursive rank()preserves the following properties:
• If key is in the table, rank() returns its index in the table, which is the same as the number of keys in the table that are smaller than key.
• If key is not in the table, rank() also returns the number of keys in the table that are smaller than key.
Recursive binary searchz
public int rank(Key key, int lo, int hi)
{
if (hi < lo) return lo;
int mid = lo + (hi - lo) / 2;
int cmp = key.compareTo(keys[mid]);
if (cmp < 0)
return rank(key, lo, mid-1);
else if (cmp > 0)
return rank(key, mid+1, hi);
else return mid;
}
Taking the time to convince yourself that the nonrecursive rank() in ALGORITHM 3.2 operates as expected (either by proving that it is equivalent to the recursive version or by proving directly that the loop always terminates with the value of lo precisely equal to the number of keys in the table that are smaller than key) is a worthwhile exercise for any programmer. (Hint: Note that lo starts at 0 and never decreases.)
Other operations
Since the keys are kept in an ordered array, most of the order-based operations are compact and straightforward, as you can see from the code on page 382. For example, a call to select(k) just returns keys[k]. We have left delete() and floor() as exercises. You are encouraged to study the implementation of ceiling() and the two-argument keys() and to work these exercises to cement your understanding of the ordered symbol-table API and this implementation.
Algorithm 3.2 Binary search in an ordered array (iterative)
public int rank(Key key)
{
int lo = 0, hi = N-1;
while (lo <= hi)
{
int mid = lo + (hi - lo) / 2;
int cmp = key.compareTo(keys[mid]);
if (cmp < 0) hi = mid - 1;
else if (cmp > 0) lo = mid + 1;
else return mid;
}
return lo;
}
This method uses the classic method described in the text to compute the number of keys in the table that are smaller than key. Compare key with the key in the middle: if it is equal, return its index; if it is less, look in the left half; if it is greater, look in the right half.
Algorithm 3.2 Ordered symbol-table operations for binary search
public Key min()
{ return keys[0]; }
public Key max()
{ return keys[N-1]; }
public Key select(int k)
{ return keys[k]; }
public Key ceiling(Key key)
{
int i = rank(key);
return keys[i];
}
public Key floor(Key key)
// See Exercise 3.1.17.
public Key delete(Key key)
// See Exercise 3.1.16.
public Iterable<Key> keys(Key lo, Key hi)
{
Queue<Key> q = new Queue<Key>();
for (int i = rank(lo); i < rank(hi); i++)
q.enqueue(keys[i]);
if (contains(hi))
q.enqueue(keys[rank(hi)]);
return q;
}
These methods, along with the methods of EXERCISE 3.1.16 and EXERCISE 3.1.17, complete the implementation of our (ordered) symbol-table API using binary search in an ordered array. The min(), max(), and select() methods are trivial, just amounting to returning the appropriate key from its known position in the array. The rank() method, which is the basis of binary search, plays a central role in the others. The floor() and delete() implementations, left for exercises, are more complicated, but still straightforward.
Analysis of binary search
The recursive implementation of rank() also leads to an immediate argument that binary search guarantees fast search, because it corresponds to a recurrence relation that describes an upper bound on the number of compares.
Proposition B. Binary search in an ordered array with N keys uses no more than lg N + 1 compares for a search (successful or unsuccessful).
Proof: This analysis is similar to (but simpler than) the analysis of mergesort (PROPOSITION F in CHAPTER 2). Let C(N) be the number of compares to search for a key in a symbol table of size N. We have C(0) = 0, C(1) = 1, and for N > 0 we can write a recurrence relationship that directly mirrors the recursive method:
C(N) ≤ C(![]() N/2
N/2![]() ) + 1.
) + 1.
Whether the search goes to the left or to the right, the size of the subarray is no more than ![]() N/2
N/2![]() , and we use one compare to check for equality and to choose whether to go left or right. When N is one less than a power of 2 (say N = 2n−1), this recurrence is not difficult to solve. First, since
, and we use one compare to check for equality and to choose whether to go left or right. When N is one less than a power of 2 (say N = 2n−1), this recurrence is not difficult to solve. First, since ![]() N/2
N/2![]() = 2n−1−1, we have
= 2n−1−1, we have
C(2n−1) ≤ C(2n−1−1) + 1.
Applying the same equation to the first term on the right, we have
C(2n−1) ≤ C(2n−2−1) + 1 + 1.
Repeating the previous step n − 2 additional times gives
C(2n−1) ≤ C(20) + n
which leaves us with the solution
C(N) = C(2n − 1) ≤ n + 1 < lg N + 1.
Exact solutions for general N are more complicated, but it is not difficult to extend this argument to establish the stated property for all values of N (see EXERCISE 3.1.20). With binary search, we achieve a logarithmic-time search guarantee.
The implementation just given for ceiling() is based on a single call to rank(), and the default two-argument size() implementation calls rank() twice, so this proof also establishes that these operations (and floor()) are supported in guaranteed logarithmic time (min(), max(), and select() are constant-time operations).
Despite its guaranteed logarithmic search, BinarySearchST still does not enable us to use clients like FrequencyCounter to solve huge problems, because the put() method is too slow. Binary search reduces the number of compares, but not the running time, because its use does not change the fact that the number of array accesses required to build a symbol table in an ordered array is quadratic in the size of the array when keys are randomly ordered (and in typical practical situations where the keys, while not random, are well-described by this model).
Proposition B (continued). Inserting a new key into an ordered array of size N uses ~ 2N array accesses in the worst case, so inserting N keys into an initially empty table uses ~ N2 array accesses in the worst case.
Proof: Same as for PROPOSITION A.

For Tale of Two Cities, with over 104 distinct keys, the cost to build the table is nearly 108 array accesses, and for the Leipzig project, with over 106 distinct keys, the cost to build the table is over 1011 array accesses. While not quite prohibitive on modern computers, these costs are extremely (and unnecessarily) high.
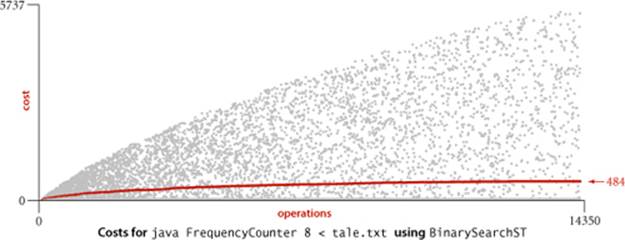
Returning to the cost of the put() operations for FrequencyCounter for words of length 8 or more, we see a reduction in the average cost from 2,246 compares (plus array accesses) per operation for SequentialSearchST to 484 for BinarySearchST. As before, this cost is even better than would be predicted by analysis, and the extra improvement is likely again explained by properties of the application (see EXERCISE 3.1.36). This improvement is impressive, but we can do much better, as you shall see.
Preview
Binary search is typically far better than sequential search and is the method of choice in numerous practical applications. For a static table (with no insert operations allowed), it is worthwhile to initialize and sort the table, as in the version of binary search that we considered in CHAPTER 1 (see page 99). Even when the bulk of the key-value pairs is known before the bulk of the searches (a common situation in applications), it is worthwhile to add to BinarySearchST a constructor that initializes and sorts the table (see EXERCISE 3.1.12). Still, binary search is infeasible for use in many other applications. For example, it fails for our Leipzig Corpora application because searches and inserts are intermixed and the table size is too large. As we have emphasized, typical modern search clients require symbol tables that can support fast implementations of both search and insert. That is, we need to be able to build huge tables where we can insert (and perhaps remove) key-value pairs in unpredictable patterns, intermixed with searches.
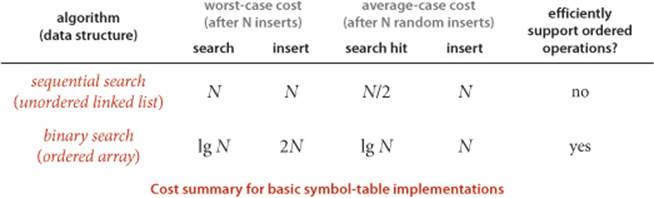
The table below summarizes performance characteristics for the elementary symbol-table implementations considered in this section. The table entries give the leading term of the cost (number of array accesses for binary search, number of compares for the others), which implies the order of growth of the running time.
The central question is whether we can devise algorithms and data structures that achieve logarithmic performance for both search and insert. The answer is a resounding yes! Providing that answer is the main thrust of this chapter. Along with the fast sort capability discussed in CHAPTER 2, fast symbol-table search/insert is one of the most important contributions of algorithmics and one of the most important steps toward the development of the rich computational infrastructure that we now enjoy.
How can we achieve this goal? To support efficient insertion, it seems that we need a linked structure. But a singly linked list forecloses the use of binary search, because the efficiency of binary search depends on our ability to get to the middle of any subarray quickly via indexing (and the only way to get to the middle of a singly linked list is to follow links). To combine the efficiency of binary search with the flexibility of linked structures, we need more complicated data structures. That combination is provided both by binary search trees, the subject of the next two sections, and by hash tables, the subject of SECTION 3.4.
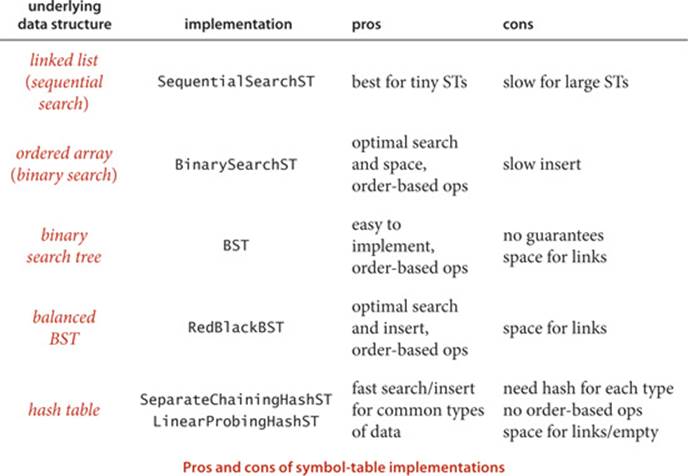
We consider six symbol-table implementations in this chapter, so a brief preview is in order. The table below is a list of the data structures, along with the primary reasons in favor of and against using each for an application. They appear in the order in which we consider them.
We will get into more detail on properties of the algorithms and implementations as we discuss them, but the brief characterizations in this table will help you keep them in a broader context as you learn them. The bottom line is that we have several fast symbol-table implementations that can be and are used to great effect in countless applications.
Q&A
Q. Why not use an Item type that implements Comparable for symbol tables, in the same way as we did for priority queues in SECTION 2.4, instead of having separate keys and values?
A. That is also a reasonable option. These two approaches illustrate two different ways to associate information with keys—we can do so implicitly by building a data type that includes the key or explicitly by separating keys from values. For symbol tables, we have chosen to highlight the associative array abstraction. Note also that a client specifies just a key in search, not a key-value aggregation.
Q. Why bother with equals()? Why not just use compareTo() throughout?
A. Not all data types lead to key values that are easy to compare, even though having a symbol table still might make sense. To take an extreme example, you may wish to use pictures or songs as keys. There is no natural way to compare them, but we can certainly test equality (with some work).
Q. Why not allow keys to take the value null?
A. We assume that Key is an Object because we use it to invoke compareTo() or equals(). But a call like a.compareTo(b) would cause a null pointer exception if a is null. By ruling out this possibility, we allow for simpler client code.
Q. Why not use a method like the less() method that we used for sorting?
A. Equality plays a special role in symbol tables, so we also would need a method for testing equality. To avoid proliferation of methods that have essentially the same function, we adopt the built-in Java methods equals() and compareTo().
Q. Why not declare key[] as Object[] (instead of Comparable[]) in BinarySearchST before casting, in the same way that val[] is declared as Object?
A. Good question. If you do so, you will get a ClassCastException because keys need to be Comparable (to ensure that entries in key[] have a compareTo() method). Thus, declaring key[] as Comparable[] is required. Delving into the details of programming-language design to explain the reasons would take us somewhat off topic. We use precisely this idiom (and nothing more complicated) in any code that uses Comparable generics and arrays throughout this book.
Q. What if we need to associate multiple values with the same key? For example, if we use Date as a key in an application, wouldn’t we have to process equal keys?
A. Maybe, maybe not. For example, you can’t have two trains arrive at the station on the same track at the same time (but they could arrive on different tracks at the same time). There are two ways to handle the situation: use some other information to disambiguate or make the value a Queue of values having the same key. We consider applications in detail in SECTION 3.5.
Q. Presorting the table as discussed on page 385 seems like a good idea. Why relegate that to an exercise (see EXERCISE 3.1.12)?
A. Indeed, this may be the method of choice in some applications. But adding a slow insert method to a data structure designed for fast search “for convenience” is a performance trap, because an unsuspecting client might intermix searches and inserts in a huge table and experience quadratic performance. Such traps are all too common, so that “buyer beware” is certainly appropriate when using software developed by others, particularly when interfaces are too wide. This problem becomes acute when a large number of methods are included “for convenience” leaving performance traps throughout, while a client might expect efficient implementations of all methods. Java’s ArrayList class is an example (see EXERCISE 3.5.27).
Exercises
3.1.1 Write a client that creates a symbol table mapping letter grades to numerical scores, as in the table below, then reads from standard input a list of letter grades and computes and prints the GPA (the average of the numbers corresponding to the grades).

3.1.2 Develop a symbol-table implementation ArrayST that uses an (unordered) array as the underlying data structure to implement our basic symbol-table API.
3.1.3 Develop a symbol-table implementation OrderedSequentialSearchST that uses an ordered linked list as the underlying data structure to implement our ordered symbol-table API.
3.1.4 Develop Time and Event ADTs that allow processing of data as in the example illustrated on page 367.
3.1.5 Implement size(), delete(), and keys() for SequentialSearchST.
3.1.6 Give the number of calls to put() and get() issued by FrequencyCounter, as a function of the number W of words and the number D of distinct words in the input.
3.1.7 What is the average number of distinct keys that FrequencyCounter will find among N random nonnegative integers less than 1,000, for N=10, 102, 103, 104, 105, and 106?
3.1.8 What is the most frequently used word of ten letters or more in Tale of Two Cities?
3.1.9 Add code to FrequencyCounter to keep track of the last call to put(). Print the last word inserted and the number of words that were processed in the input stream prior to this insertion. Run your program for tale.txt with length cutoffs 1, 8, and 10.
3.1.10 Give a trace of the process of inserting the keys E A S Y Q U E S T I O N into an initially empty table using SequentialSearchST. How many compares are involved?
3.1.11 Give a trace of the process of inserting the keys E A S Y Q U E S T I O N into an initially empty table using BinarySearchST. How many compares are involved?
3.1.12 Modify BinarySearchST to maintain one array of Item objects that contain keys and values, rather than two parallel arrays. Add a constructor that takes an array of Item values as argument and uses mergesort to sort the array.
3.1.13 Which of the symbol-table implementations in this section would you use for an application that does 103 put() operations and 106 get() operations, randomly intermixed? Justify your answer.
3.1.14 Which of the symbol-table implementations in this section would you use for an application that does 106 put() operations and 103 get() operations, randomly intermixed? Justify your answer.
3.1.15 Assume that searches are 1,000 times more frequent than insertions for a BinarySearchST client. Estimate the percentage of the total time that is devoted to insertions, when the number of searches is 103, 106, and 109.
3.1.16 Implement the delete() method for BinarySearchST.
3.1.17 Implement the floor() method for BinarySearchST.
3.1.18 Prove that the rank() method in BinarySearchST is correct.
3.1.19 Modify FrequencyCounter to print all of the values having the highest frequency of occurrence, not just one of them. Hint: Use a Queue.
3.1.20 Complete the proof of PROPOSITION B (show that it holds for all values of N). Hint: Start by showing that C(N) is monotonic: C(N) ≤ C(N+1) for all N > 0.
Creative Problems
3.1.21 Memory usage. Compare the memory usage of BinarySearchST with that of SequentialSearchST for N key-value pairs, under the assumptions described in SECTION 1.4. Do not count the memory for the keys and values themselves, but do count references to them. For BinarySearchST, assume that array resizing is used, so that the array is between 25 percent and 100 percent full.
3.1.22 Self-organizing search. A self-organizing search algorithm is one that rearranges items to make those that are accessed frequently likely to be found early in the search. Modify your search implementation for EXERCISE 3.1.2 to perform the following action on every search hit: move the key-value pair found to the beginning of the list, moving all pairs between the beginning of the list and the vacated position to the right one position. This procedure is called the move-to-front heuristic.
3.1.23 Analysis of binary search. Prove that the maximum number of compares used for a binary search in a table of size N is precisely the number of bits in the binary representation of N, because the operation of shifting 1 bit to the right converts the binary representation of N into the binary representation of ![]() N/2
N/2![]() .
.
3.1.24 Interpolation search. Suppose that arithmetic operations are allowed on keys (for example, they may be Double or Integer values). Write a version of binary search that mimics the process of looking near the beginning of a dictionary when the word begins with a letter near the beginning of the alphabet. Specifically, if kx is the key value sought, klo is the key value of the first key in the table, and khi is the key value of the last key in the table, look first ![]() (kx − klo)/(khi − klo)
(kx − klo)/(khi − klo)![]() -way through the table, not half-way. Test your implementation against BinarySearchST for FrequencyCounter.
-way through the table, not half-way. Test your implementation against BinarySearchST for FrequencyCounter.
3.1.25 Software caching. Since the default implementation of contains() calls get(), the inner loop of FrequencyCounter
if (!st.contains(word)) st.put(word, 1);
else st.put(word, st.get(word) + 1);
leads to two or three searches for the same key. To enable clear client code like this without sacrificing efficiency, we can use a technique known as software caching, where we save the location of the most recently accessed key in an instance variable. Modify SequentialSearchST and BinarySearchSTto take advantage of this idea.
3.1.26 Frequency count from a dictionary. Modify FrequencyCounter to take the name of a dictionary file as its argument, count frequencies of the words from standard input that are also in that file, and print two tables of the words with their frequencies, one sorted by frequency, the other sorted in the order found in the dictionary file.
3.1.27 Small tables. Suppose that a BinarySearchST client has S search operations and N distinct keys. Give the order of growth of S such that the cost of building the table is the same as the cost of all the searches.
3.1.28 Ordered insertions. Modify BinarySearchST so that inserting a key that is larger than all keys in the table takes constant time (so that building a table by calling put() for keys that are in order takes linear time).
3.1.29 Test client. Write a test client for BinarySearchST that tests the implementations of min(), max(), floor(), ceiling(), select(), rank(), deleteMin(), deleteMax(), and keys() that are given in the text. Start with the standard indexing client given on page 370. Add code to take additional command-line arguments, as appropriate.
3.1.30 Certification. Add assert statements to BinarySearchST to check algorithm invariants and data structure integrity after every insertion and deletion. For example, every index i should always be equal to rank(select(i)) and the array should always be in order.
Experiments
3.1.31 Performance driver. Write a performance driver program that uses put() to fill a symbol table, then uses get() such that each key in the table is hit an average of ten times and there is about the same number of misses, doing so multiple times on random sequences of string keys of various lengths ranging from 2 to 50 characters; measures the time taken for each run; and prints out or plots the average running times.
3.1.32 Exercise driver. Write an exercise driver program that uses the methods in our ordered symbol-table API on difficult or pathological cases that might turn up in practical applications. Simple examples include key sequences that are already in order, key sequences in reverse order, key sequences where all keys are the same, and keys consisting of only two distinct values.
3.1.33 Driver for self-organizing search. Write a driver program for self-organizing search implementations (see EXERCISE 3.1.22) that uses put() to fill a symbol table with N keys, then does 10 N successful searches according to a predefined probability distribution. Use this driver to compare the running time of your implementation from EXERCISE 3.1.22 with BinarySearchST for N = 103, 104, 105, and 106 using the probability distribution where search hits the ith smallest key with probability 1/2i.
3.1.34 Zipf’s law. Do the previous exercise for the probability distribution where search hits the ith smallest key with probability 1/(iHN) where HN is a Harmonic number (see page 185). This distribution is called Zipf’s law. Compare the move-to-front heuristic with the optimal arrangement for the distributions in the previous exercise, which is to keep the keys in increasing order (decreasing order of their expected frequency).
3.1.35 Performance validation I. Run doubling tests that use the first N words of Tale of Two Cities for various values of N to test the hypothesis that the running time of FrequencyCounter is quadratic when it uses SequentialSearchST for its symbol table.
3.1.36 Performance validation II. Explain why the performance of BinarySearchST and SequentialSearchST for FrequencyCounter is even better than predicted by analysis.
3.1.37 Put/get ratio. Determine empirically the ratio of the amount of time that BinarySearchST spends on put() operations to the time that it spends on get() operations when FrequencyCounter is used to find the frequency of occurrence of values in 1 million random M-bit int values, for M = 10, 20, and 30. Answer the same question for tale.txt and compare the results.
3.1.38 Amortized cost plots. Develop instrumentation for FrequencyCounter, SequentialSearchST, and BinarySearchST so that you can produce plots like the ones in this section showing the cost of each put() operation during the computation.
3.1.39 Actual timings. Instrument FrequencyCounter to use Stopwatch and StdDraw to make a plot where the x-axis is the number of calls on get() or put() and the y-axis is the total running time, with a point plotted of the cumulative time after each call. Run your program for Tale of Two Cities usingSequentialSearchST and again using BinarySearchST and discuss the results. Note: Sharp jumps in the curve may be explained by caching, which is beyond the scope of this question.
3.1.40 Crossover to binary search. Find the values of N for which binary search in a symbol table of size N becomes 10, 100, and 1,000 times faster than sequential search. Predict the values with analysis and verify them experimentally.
3.1.41 Crossover to interpolation search. Find the values of N for which interpolation search in a symbol table of size N becomes 1, 2, and 10 times faster than binary search, assuming the keys to be random 32-bit integers (see EXERCISE 3.1.24). Predict the values with analysis, and verify them experimentally.
All materials on the site are licensed Creative Commons Attribution-Sharealike 3.0 Unported CC BY-SA 3.0 & GNU Free Documentation License (GFDL)
If you are the copyright holder of any material contained on our site and intend to remove it, please contact our site administrator for approval.
© 2016-2026 All site design rights belong to S.Y.A.