From Mathematics to Generic Programming (2011)
13. A Real-World Application
I am fairly familiar with all forms of secret writings, and am myself the author of a trifling monograph upon the subject, in which I analyze one hundred and sixty separate ciphers, but I confess that this is entirely new to me.
Sherlock Holmes
Throughout this book, we’ve seen examples of important algorithms that came out of work on number theory. We’ve also seen how attempts to generalize those mathematical results brought about the development of abstract algebra, and how its ideas about abstraction led directly to the principles of generic programming. Now we’re going put it all together. We’ll show how our mathematical results and our generalized algorithms can be used to implement a real-world application: a particular kind of system for secure communication, known as a public-key cryptosystem.
13.1 Cryptology
Cryptology is the science of secret communication. Cryptography is concerned with developing codes and ciphers;1 cryptanalysis with breaking them.
1 Technically, a code is a system for secret communication where a meaningful concept such as the name of a person, place, or event is replaced with some other text, while a cipher is a system for modifying text at the level of its representation (letters or bits). But we’ll use the terms interchangeably; in particular, we’ll use encode and decode informally to mean encipher and decipher.
The idea of sending secret messages dates back to ancient times, with examples of cryptography in many societies including Sparta and Persia. Julius Caesar used the technique of replacing letters with those in a “rotated” alphabet (now known as the Caesar cipher) to send military messages. In the 19th century, cryptography and “cryptograms,” puzzles that use a simple substitution cipher, caught the public’s imagination. In an 1839 magazine article, Edgar Allen Poe claimed he could decipher any such messages his readers submitted—and apparently succeeded. A few years later he published a short story called “The Gold Bug,” which includes an account of how to break such a code. A substitution cipher also featured prominently, several decades later, in Sir Arthur Conan Doyle’s Sherlock Holmes mystery, “The Adventure of the Dancing Men.”
But the importance of cryptography went well beyond casual entertainment. Codes and ciphers played an important role in diplomacy, espionage, and warfare. By the early 20th century, creating better cryptographic schemes was a top priority for the military of the world’s leading powers. The ability to break these codes could make the difference between success and failure on the battlefield.
Bletchley Park and the Development of Computers
In World War II, the main British cryptanalysis group was based at an estate in the countryside called Bletchley Park. At the time, the German navy was using an enhanced version of a commercial encryption mechanism called the Enigma machine. An earlier version of the Engima had been cracked by Polish cryptographer Marian Rejewski, using an electromechanical device that tested many possible Enigma settings in parallel.
At Bletchley Park, a brilliant young mathematician named Alan Turing, whose previous work provided much of the foundations of what became computer science, designed a much more sophisticated version of Rejewski’s device called a “bombe.” Through the work of Turing and many others, the Allies were able to decipher the Enigma messages, a great help in winning the war.
Another encryption mechanism used by the Nazis was called the Lorenz machine. To break the Lorenz cipher, the British cryptographers realized that the electromechanical bombes were not fast enough. So an engineer named Tommy Flowers designed a much more powerful electronic device using vacuum tubes, called “Colossus.” Although it was not a general-purpose machine and was only partially programmable, Colossus may have been the world’s first programmable electronic digital computer.
A cryptosystem consists of algorithms for encrypting and decrypting data. The original data is called the plaintext, and the encrypted data is called the ciphertext. A set of keys determine the behavior of the encryption and decryption algorithms:
ciphertext = encryption(key0, plaintext)
plaintext = decryption(key1, ciphertext)
The system is symmetric if key0 = key1; otherwise, it is asymmetric.
Many early cryptosystems were symmetric and used secret keys. The problem with this is that the sender and the receiver of the message both must have the keys in advance. If the key is compromised and the sender wants to switch to a new one, he has the additional problem of figuring out how to secretly convey the new key to the receiver.
* * *
A public-key cryptosystem is an encryption scheme that makes use of a pair of keys: a public key pub for encrypting, and a private key prv for decrypting. If Alice wants to send a message to Bob, she encrypts the message with Bob’s public key. The ciphertext is then unreadable to anyone but Bob, who uses his private key to decrypt the message.
To have a public-key cryptosystem, the following requirements must be satisfied:
1. The encryption function needs to be a one-way function: easy to compute, with an inverse that is hard to compute. Here, “hard” has its technical computer science meaning of taking exponential time—in this case, exponential in the size of the key.
2. The inverse function has to be easy to compute when you have access to a certain additional piece of information, known as the trapdoor.
3. Both encryption and decryption algorithms are publicly known. This ensures the confidence of all parties in the technique being used.
A function meeting the first two requirements is known as a trapdoor one-way function.
Perhaps the best-known and most widely used public-key cryptosystem is the RSA algorithm, named after its creators (Rivest, Shamir, and Adleman). As we’ll see shortly, RSA depends on some mathematical results about primes.
Who Invented Public-Key Cryptography?
For years, it was believed that Stanford professor Martin Hellman, together with two graduate students, Whitfield Diffie and Ralph Merkle, invented public-key cryptography in 1976. They proposed how such a system would work, and realized it would require a trapdoor one-way function. Unfortunately, they didn’t give an example of such a function—it was just a hypothetical construct. In 1977, MIT researchers Ron Rivest, Adi Shamir, and Len Adleman came up with a procedure for creating a trapdoor one-way function, which became known as the RSA algorithm after the inventors’ initials.
In 1997, the British government disclosed that one of their intelligence researchers, Clifford Cocks, had actually invented a special case of RSA in 1973—but it took 20 years after the publication of the RSA algorithm before they declassified Cocks’ memo. After that, Admiral Bobby Ray Inman, the former head of the U.S. National Security Agency, claimed that his agency had invented some sort of public-key cryptographic technique even earlier, in the 1960s, although no evidence was given. Who knows which country’s intelligence agency will come forward next with an earlier claim?
13.2 Primality Testing
The problem of distinguishing prime numbers from composite ... is known to be one of the most important and useful in arithmetic.
C. F. Gauss, Disquisitiones Arithmeticae
An important problem in modern cryptography is determining whether an integer is prime. Gauss believed that (1) deciding whether a number is prime or composite is a very hard problem, and so is (2) factoring a number. He was wrong about #1, as we shall see. So far, he seems to be right about #2, which is a good thing for us, since modern cryptosystems are based on this assumption.
To find out if a number n is prime, it helps to have a predicate that tells us whether it’s divisible by a given number i:
Click here to view code image
template <Integer I>
bool divides(const I& i, const I& n) {
return n % i == I(0);
}
We can call this repeatedly to find the smallest divisor of a given number n. Just as we did with the Sieve of Eratosthenes in Chapter 3, our loop for testing divisors will start at 3, advance by 2, and stop when the square of the current candidate reaches n:
Click here to view code image
template <Integer I>
I smallest_divisor(I n) {
// precondition: n > 0
if (even(n)) return I(2);
for (I i(3); i * i <= n; i += I(2)) {
if (divides(i, n)) return i;
}
return n;
}
Now we can create a simple function to determine whether n is prime:
Click here to view code image
template <Integer I>
I is_prime(const I& n) {
return n > I(1) && smallest_divisor(n) == n;
}
This is mathematically correct, but it’s not going to be fast enough. Its complexity is ![]() . That is, it’s exponential in the number of digits. If we want to test a 200-digit number, we may be waiting for more time than the life of the universe.
. That is, it’s exponential in the number of digits. If we want to test a 200-digit number, we may be waiting for more time than the life of the universe.
To overcome this problem, we’re going to need a different approach, which will rely on the ability to do modular multiplication. We’ll use a function object that provides what we need:
Click here to view code image
template <Integer I>
struct modulo_multiply {
I modulus;
modulo_multiply(const I& i) : modulus(i) {}
I operator() (const I& n, const I& m) const {
return (n * m) % modulus;
}
};
We’ll also need an identity element:
Click here to view code image
template <Integer I>
I identity_element(const modulo_multiply<I>&) {
return I(1);
}
Now we can compute a multiplicative inverse modulo prime p. It uses the result we showed in Chapter 5 that, as a consequence of Fermat’s Little Theorem, the inverse of an integer a, where 0 < a < p, is ap−2 (see Section 5.4, right after the proof of Fermat’s Little Theorem). It also uses the power function we created in Chapter 7:
Click here to view code image
template <Integer I>
I multiplicative_inverse_fermat(I a, I p) {
// precondition: p is prime & a > 0
return power_monoid(a, p - 2, modulo_multiply<I>(p));
}
With these pieces, we can now use Fermat’s Little Theorem to test if a number n is prime. Recall that Fermat’s Little Theorem says:
If p is prime, then ap−1 − 1 is divisible by p for any 0 < a < p.
Equivalently:
If p is prime, then ap–1 = 1 mod p for any 0 < a < p.
We want to know if n is prime. So we take an arbitrary number a smaller than n, raise it to the n − 1 power using modular multiplication (mod n), and check if the result is 1. (We call the number a we’re using a witness.) If the result is not equal to 1, we know definitely by the contrapositive of the theorem that n is not prime. If the result is equal to 1, we know that there’s a good chance that n is prime, and if we do this for lots of random witnesses, there’s a very good chance that it is prime:
Click here to view code image
template <Integer I>
bool fermat_test(I n, I witness) {
// precondition: 0 < witness < n
I remainder(power_semigroup(witness,
n - I(1),
modulo_multiply<I>(n)));
return remainder == I(1);
}
This time we use power_semigroup instead of power_monoid, because we know we’re not going to be raising anything to the power 0. The Fermat test is very fast, because we have a fast way to raise a number to a power—our O(log n) generalized Egyptian multiplication algorithm from Chapter 7.
* * *
While the Fermat test works the vast majority of the time, it turns out that there are some pathological cases of numbers that will fool it for all witnesses coprime to n; they produce remainders of 1 even though they’re composite. These are called Carmichael numbers.
Definition 13.1. A composite number n > 1 is a Carmichael number if and only if
∀b > 1, coprime(b, n) ![]() bn−1 = 1 mod n
bn−1 = 1 mod n
172081 is an example of a Carmichael number. Its prime factorization is 7 · 13 · 31 · 61.
Exercise 13.1. Implement the function:
bool is_carmichael(n)
Exercise 13.2. Find the first seven Carmichael numbers using your function from Exercise 13.1.
13.3 The Miller-Rabin Test
To avoid worrying about Carmichael numbers, we’re going to use an improved version of our primality tester, called the Miller-Rabin test; it will again rely on the speed of our power algorithm.
We know that n − 1 is even (it would be awfully silly to run a primality test on an even n), so we can represent n − 1 as the product 2k · q. The Miller-Rabin test uses a sequence of squares w20q, w21q, ..., w2kq, where w is a random number less than the one we are testing. The last exponent in this sequence is n − 1, the same value the Fermat test uses; we’ll see why this is important shortly.
We’re also going to rely on the self-canceling law (Lemma 5.3), except we’ll write it with new variable names and assuming modular multiplication:
For any 0 < x < n ∧ prime(n), x2 = 1 mod n ![]() x = 1 ∨ x = −1
x = 1 ∨ x = −1
Remember that in modular arithmetic, −1 mod n is the same as (n − 1) mod n, a fact that we rely on in the following code. If we find some x2 = 1 mod n where x is neither 1 nor −1, then n is not prime.
Now we can make two observations: (1) If x2 = 1 mod n, then there’s no point in squaring x again, because the result won’t change; if we reach 1, we’re done. (2) If x2 = 1 mod n and x is not −1, then we know n is not prime (since we already ruled out x = 1 earlier in the code).
Here’s the code, which returns true if n is probably prime, and false if it definitely is not:
Click here to view code image
template <Integer I>
bool miller_rabin_test(I n, I q, I k, I w) {
// precondition n > 1 ∧ n – 1 = 2kq ∧ q is odd
modulo_multiply<I> mmult(n);
I x = power_semigroup(w, q, mmult);
if (x == I(1) || x == n - I(1)) return true;
for (I i(1); i < k; ++i) {
// invariant x = w2i – 1 q
x = mmult(x, x);
if (x == n - I(1)) return true;
if (x == I(1)) return false;
}
return false;
}
Note that we pass in q and k as arguments. Since we’re going to call the function many times with different witnesses, we don’t want to refactor n – 1 every time.
Why can we return true at the beginning if the power_semigroup call returns 1 or – 1? Because we know that squaring the result will give 1, and squaring is equivalent to multiplying the exponent in the power calculation by a factor of 2, and doing this k times will make the exponent n – 1, the value we need for Fermat’s Little Theorem to hold. In other words, if wq mod n = 1 or –1, then w2k q mod n = wn – 1 mod n = 1.
Let’s look at an example. Suppose we want to know if n = 2793 is prime. We choose a random witness w = 150. We factor n – 1 = 2792 into 22 · 349, so q = 349 and k = 2. We compute
x = wq mod n = 150349 mod 2793 = 2019
Since the result is neither 1 nor – 1, we start squaring x:
i = 1; x2 = 15021 ·349 mod 2793 = 1374
i = 2; x2 = 15022 ·349 mod 2793 = 2601
Since we haven’t reached 1 or – 1 yet, and i = k, we can stop and return false; 2793 is not prime.
Like the Fermat test, the Miller-Rabin test is right most of the time. Unlike the Fermat test, the Miller-Rabin test has a provable guarantee: it is right at least 75% of the time2 for a random witness w. (In practice, it’s even more often.) Randomly choosing, say, 100 witnesses makes the probability of error less than 1 in 2200. As Knuth remarked, “It is much more likely that our computer has dropped a bit, due ... to cosmic radiations.”
2 In fact, the requirement that q must be odd is needed for this probability guarantee.
AKS: A New Test for Primality
In 2002, Neeraj Kayal and Nitin Saxena, two undergraduate students at the Indian Institute of Technology at Kanpur, together with their advisor, Manindra Agrawal, came up with a deterministic polynomial-time algorithm for primality testing, and published their result. This is a problem that people in number theory had been working on for centuries.
There is a very clear paper by Andrew Granville describing the technique. Although it is a dense mathematical paper, it is understandable to a surprisingly wide audience. This is unusual; most important mathematical results being published in recent decades require years of prior mathematical study to be understood. Determined readers who are willing to put in serious effort are encouraged to read it.
Despite the fact that the AKS algorithm is a great accomplishment, we’re not going to use it here, because the probabilistic Miller-Rabin algorithm is still considerably faster.
13.4 The RSA Algorithm: How and Why It Works
The RSA algorithm is one of the most important and widely used cryptosystems in use today. It is often used for authentication—to prove that users, companies, websites, and other entities with an online presence are who they say they are. It is also often used to exchange private keys that are used in a separate, faster symmetric cryptosystem used to encode data being communicated.
Some of the important communication protocols that use RSA are:

We use many of these protocols daily. For example, anytime you visit a “secure” website (one whose URL has an https prefix), you’re relying on SSL/TLS, which in turn uses RSA or (depending on the implementation) a similar public-key cryptosystem.
RSA relies on the mathematical results we’ve just shown for primality testing. RSA requires two steps: key generation, which needs to be done only rarely, and encoding/decoding, which is done every time a message is sent or received.
Key generation works as follows. First, the following values are computed:
• Two random large primes, p1 and p2 (the Miller-Rabin test makes this feasible)
• Their product, n = p1p2
• The Euler function of their product, which we can compute using Equation 5.5 from Chapter 5: φ (p1p2) = (p1 – 1) (p2 – 1)
• A random public key pub, coprime with φ(p1p2)
• A private key prv, the multiplicative inverse of pub modulo φ (p1p2) (To compute this, we’ll use the extended GCD function we derived in Chapter 12.)
When these computations are complete, p1 and p2 are destroyed; pub and n are published, and prv is kept secret. At this point, there is no feasible way to factor n, since it is such a large number with such large factors.
The encoding and decoding process is simpler. The text is divided into equalsize blocks, say 256 bytes long, which are interpreted as large integers. The message block size s must be chosen so that n > 2 s. To encode a plaintext block, we use our familiar power algorithm:
Click here to view code image
power_semigroup(plaintext_block, pub, modulo_multiply<I>(n));
Decoding looks like this:
Click here to view code image
power_semigroup(ciphertext_block, prv, modulo_multiply<I>(n));
Observe that we do exactly the same operation to encode and decode. The only difference is which text and which key we pass in.
* * *
How does RSA work? Encryption consists of raising a message m to a power pub; decryption consists of raising the result to the power prv. We need to show that the result of applying these two operations is the original message m (modulo n):
(mpub)prv = m mod n
Proof. Recall that we specifically created prv to be the multiplicative inverse of pub modulo φ (p1p2), so by definition, the product of pub and prv is some multiple q of φ (p1p2) with a remainder of 1. We can make that substitution in the exponent on the right.
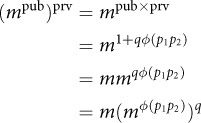
Now we can apply Euler’s theorem from Chapter 5, which says that aφ (n) – 1 is divisible by n; that is, a φ (n) = 1 + vn. Making that substitution, we have
= m (1 + vn) q
When we expand (1 + vn) q, every term will be a multiple of n except 1, so we can collapse all of these and just say we have 1 plus some other multiple of n:
= m + wn
= m mod n
![]()
The Euler theorem step depends on m being coprime with n = p1p2. Since the message m could be anything, how do we know that it will be coprime to p1p2? Since p1 and p2 are enormous primes, that probability is practically indistinguishable from 1, and people normally do not worry about it. However, if you want to address this, you can add one extra byte to the end of m. The extra byte is not actually part of the message, but is there only to ensure that we have a coprime. When we create m, we check whether it is coprime; if it isn’t, we simply add 1 to this extra byte.
* * *
Why does RSA work? In other words, why do we believe it’s secure? The reason is that factoring is hard, and therefore computing φ is not feasible. Perhaps if quantum computers prove to be realizable in the future, it will be possible to run an exponential number of divisor tests in parallel, making factoring a tractable problem. But for now, we can rely on RSA for many secure communications applications.
Project
Exercise 13.3. Implement an RSA key generation library.
Exercise 13.4. Implement an RSA message encoder/decoder that takes a string and the key as its arguments.
Hints:
• If your language does not support arbitrary-precision integers, you’ll need to install a package for handling them.
• Remember that two numbers are coprime if their GCD is 1. This will come in handy for one of the key generation steps.
• You’ll need the results that we derived in Chapter 12. There are two relevant functions, extended_gcd and multiplicative_inverse.
Recall that the extended_gcd function from Chapter 12 returns a pair (x,y) such that ax + ny = gcd(a,n). You can use this function to check for coprimes. It’s also part of the implementation of multiplicative_inverse, a function that returns the multiplicative inverse of a modulo n if it exists, or 0 if it does not. Unlike the function multiplicative_inverse_fermat that we introduced in Section 13.2, this one works for any n, not just primes:
Click here to view code image
template <Integer I>
I multiplicative_inverse(I a, I n) {
std::pair<I, I> p = extended_gcd(a, n);
if (p.second != I(1)) return I(0);
if (p.first < I(0)) return p.first + n;
return p.first;
}
You’ll need this to get the private key from the public key.
13.5 Thoughts on the Chapter
Issues of identity, privacy, and security are becoming increasingly important as more of our personal data lives online and more of our personal communication travels over the Internet. As we have seen, many important protocols for keeping data private and secure from tampering rely on RSA or similar publickey cryptosystems for authentication, exchange of keys used for encryption, or other security features.
These important practical capabilities owe their existence to results from one of the most theoretical branches of mathematics, number theory. There is a perception among programmers that mathematicians are people who don’t know or care about practical concerns and that mathematics, particularly in its more abstract areas, has little practical value. Looking at the history, we can see that both of these perceptions are false. The greatest mathematicians enthusiastically worked on extremely practical problems—for example, Gauss worked on one of the first electromechanical telegraphs, and Poincaré spent years developing time zones. Perhaps more importantly, it is impossible to know which theoretical ideas are going to have practical applications.