Plan, Activity, and Intent Recognition: Theory and Practice, FIRST EDITION (2014)

Part III. Modeling Human Cognition

Chapter 8. Decision-Theoretic Planning in Multiagent Settings with Application to Behavioral Modeling

Prashant Doshi, Xia Qu and Adam Goodie, University of Georgia, Athens, GA, USA

Abstract

Optimal planning in environments shared with other interacting agents often involves recognizing the intent of others and their plans. This is because others’ actions may impact the state of the environment and, consequently, the efficacy of the agent’s plan. Planning becomes further complicated in the presence of uncertainty, which may manifest due to the state being partially observable, nondeterminism in how the dynamic state changes, and imperfect sensors. A framework for decision–theoretic planning in this space is the interactive partially observable Markov decision process (I-POMDP), which generalizes the well-known POMDP to multiagent settings. This chapter describes the general I-POMDP framework and a particular approximation that facilitates its usage. Because I-POMDPs elegantly integrate beliefs and the modeling of others in the subject agent’s decision process, they apply to modeling human behavioral data obtained from strategic games. We explore the effectiveness of models based on simplified I-POMDPs in fitting experimental data onto theory-of-mind–based recursive reasoning.

Keywords

Behavioral models

Experimental data

Modeling other agents

Nested beliefs

Planning

Recursive thinking

Uncertainty

Acknowledgments

We acknowledge grant support from the U.S. Air Force, #FA9550-08-1-0429, and from the National Science Foundation, CAREER #IIS-0845036. All opinions expressed in this article are those of the authors alone and do not reflect on the funding agencies in any way.

8.1 Introduction

Partially observable Markov decision processes (POMDP) [28,44] offer a formal approach for decision–theoretic planning in contexts that are uncertain. This type of planning involves deciding on a sequence of actions that is expected to be optimal under the uncertainty. In particular, the framework is appropriate for planning given uncertainty about the physical state and action outcomes, using observations that reveal partial information about the current state. Consequently, a decision–theoretic “universal plan,” also called a policy, is typically a mapping from a sequence of observations of increasing length to the optimal action.

Although a policy is similar in its representation to a contingent plan for classical nondeterministic domains [27], it is usually associated with a guarantee of optimality while the contingent plans are often outcomes of fast heuristic search. Because observation sequences could become very long with time, POMDPs usually maintain probability distributions over the state space called beliefs, which are sufficient statistics for the observation history and provide for a compact policy representation. Littman [30] provides a generally accessible tutorial on POMDPs for obtaining a detailed background.

The basic formulation of POMDPs may not be adequate if the context also includes other interacting agents that observe and act. This is because others’ actions may disturb the plan in various ways. We could include a fixed marginal distribution over others’ actions within the POMDP as a way of anticipating how others act. However, this form of implicit modeling would be naive because other agents’ behaviors often evolve with time. Consequently, more sophisticated generalizations that provide explicit support for modeling other agents are needed for decision–theoretic planning in multiagent settings.

A framework that generalizes POMDPs to multiagent settings is the decentralized POMDP (Dec-POMDP) [4]. This framework provides a vector of decision–theoretic plans—one for each agent—in a cooperative setting. Another generalization is the interactive POMDP (I-POMDP) framework [22], which generalizes the state space of the problem to include behavioral models of the other agents; these are updated over time and a plan is formulated in response to these models’ distribution.

The interaction context in a multiagent setting may range from complete cooperation among the agents to strict competition. As we may include computable models of any type in the state space, the I-POMDP framework has the attractive property of being applicable in situations where agents may have identical or conflicting objectives, thereby modeling interaction contexts that are varied compared to the common rewards in Dec-POMDPs [14].

In this chapter, we focus on the I-POMDP framework because of its relevance to the topics covered in this book. The key difference from a POMDP is that I-POMDPs define an interactive state space, which combines the traditional physical state space with explicit models of other agents sharing the environment in order to predict their behavior. Inspired in part by Dennett’s intentional stance [13], the framework categorizes models into those that are intentional and others that are subintentional. Intentional models ascribe beliefs, capabilities, and preferences to others, assuming that the agent is Bayesian and rational, and could themselves be I-POMDPs. Examples of subintentional models include probability distributions and finite-state controllers.

The notion of learning the models of other agents in an I-POMDP is generally similar to Bayesian approaches for probabilistic plan recognition, especially those that perform weighted model counting [19]. Early implementations of plan recognition inferred the likelihood of the models from observing the other agents’ actions directly. We may also use general-purpose Bayesian networks for plan recognition [10,11], which allows for inference over the models using observations of the effect that others’ actions may have on the subject agent’s state. Such inferential modeling is an integral part of I-POMDPs, making the framework an appropriate choice for this problem and its subsequent use for planning. Furthermore, I-POMDPs account for agents’ nested modeling of others as intentional agents.

Investigations reveal that human recursive thinking of the sort, what do you think that I think that you think, often vital to recognizing intent, tends to be shallow by default [9,17,26]. Camerer et al. [9], for example, concludes that typical recursive reasoning could go no deeper than two or even one level. However, recent experiments [23,33] show that human recursive thinking could generally go deeper than previously thought in competitive situations. Because I-POMDPs consider recursive beliefs, they are a natural choice as a point of departure for computationally modeling the behavioral data collected in the experiments.

We apply them augmented with well-known human learning and behavioral models in order to model human data that are consistent with three levels of recursive reasoning in fixed-sum games. We compare the performance of the I-POMDP-based models to the use of weighted fictitious play [12] for modeling the data. Instead of ascertaining the opponent’s mental models, weighted fictitious play relies exclusively on past patterns of the opponent’s actions. In the broader context, Camerer [8] provides a detailed survey of behavioral experiments in strategic settings and the implications for game theory.

The remainder of the chapter is structured as follows. We describe in detail the I-POMDP framework and its finitely nested approximation in Section 8.2. In this section, we outline its formal definition and discuss the key steps involving the belief update and value iteration that underpin the solution of I-POMDPs. Next, in Section 8.3, we focus on an application of I-POMDPs to modeling human behavior in games of strategy. We briefly describe the study and the data that we seek to model; subsequently, we explore multiple computational models of the behavioral data, two of which are based on I-POMDPs. We end this chapter with a brief summary discussion in Section 8.4.

8.2 The Interactive POMDP Framework

The presence of other agents in a shared environment complicates planning because other agents’ actions may impact the state of the planning problem as well. Although the planning process could remain oblivious of others, this would likely make the policy suboptimal. Therefore interactive POMDPs generalize POMDPs to multiagent settings by explicitly including models of the other agents as part of the state space [22]. For clarity, we focus on a setting shared by two agents, and , although the framework naturally extends to multiple agents.

The I-POMDP for an agent, , in a setting with one other agent, , is mathematically defined as:

where

is the set of interactive states defined as . Here, is the set of physical states and is the set of computable models of the other agent, .

is the set of joint actions of the agents.

is the set of observations of agent .

models the probabilistic transitions between the physical states. Mathematically, is a function that maps each transition between states on performing a joint action to its probability, . Notice that we do not include transitions between models because we assume that actions do not manipulate the (mental) models directly.

represents the observational capabilities of the agent and is a function that maps observations in a state resulting from joint actions to a probability distribution, . We assume that models may not be observed directly and therefore do not include them in .

gives the immediate reward obtained by agent conditioned on the physical state and the joint action. Another interpretation of is that it models the preferences of agent .

is the criterion under which the reward is optimized. This is often an optimization of the summed reward over a finite set of timesteps, or of the summation of the geometrically discounted reward over an infinite set of timesteps in the limit.

We subdivide the set of computable models of the other agent, , into those that are intentional, and the remaining are subintentional. Intentional models, denoted by , are analogous to types as in game theory [25] and ascribe beliefs, capabilities, and preferences to the other agent. These are abstractions that constitute Dennett’s intentional stance [13] and allow for a reasoned prediction of the other agent’s behavior using well-studied mental constructs.

An intentional model of agent , consists of ’s belief, , and ’s frame, , where the parameters of agent are defined analogously to the preceding. Because could be modeling agent intentionally, the belief could be infinitely nested. Subintentional models, on the other hand, include finite-state automatons and probability distributions over the agent’s actions, and scant attention is paid to how we arrive at such models.

8.2.1 Finitely Nested I-POMDP

Infinitely nested beliefs pose challenges for making the framework operational. An obvious challenge is that of noncomputability of the belief system; other challenges include some impossible belief systems that could arise in infinitely nested beliefs, as noted by Binmore [5] and Brandenburger [6]. A natural way to enable computability is to truncate the beliefs to finite levels by defining level 0 beliefs. Finite nestings, additionally, avoid the impossible beliefs. This leads to a finitely nested framework, , with denoting the level, which approximates the original I-POMDP outlined in the previous section.

Such beliefs are similar to the hierarchical belief systems discussed in game theory in order to define universal type spaces [7,35] and formalize interactive epistemology [1,2]. Specifically, level 0 interactive states are just the physical states and level 0 beliefs are probability distributions over the level 0 states. Subsequently, level 0 models contain level 0 intentional models—each of which consists of a level 0 belief and the frame—and subintentional models. Level 1 interactive states are combinations of the physical states and level 0 models of the other agent. Level 1 beliefs are distributions over the level 1 interactive states, and level 1 models contain level 1 intentional models and level 0 models.

We construct higher levels analogously:

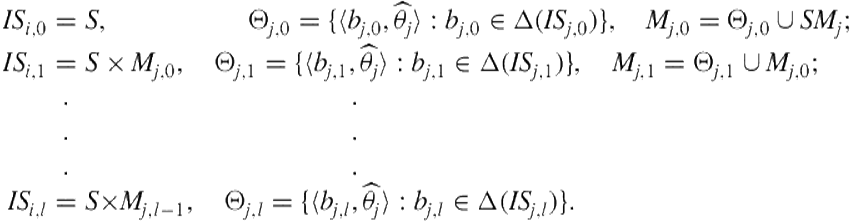
Notice that the level interactive state space contains models of all levels up to . A common simplifying approximation, which we adopt from here onward, is to consider models of the previous level only.

8.2.2 Bayesian Belief Update

Because of partial observability, the solution approach maintains a belief over the interactive states, which is a sufficient statistic fully summarizing the observation history. Beliefs are updated after the subject agent’s action and observation using Bayes rule, and a key step involves inferring the other agents’ models from observations, which has similarities with Bayesian plan recognition.

Two differences complicate the belief update in multiagent settings. First, because the state of the physical environment depends on the actions performed by all agents, the prediction of how it changes has to be made based on the probabilities of various actions of the other agent. Probabilities of the other’s actions are obtained by solving its models. Agents attempt to infer which actions other agents have performed by sensing their results on the environment. Second, and of greater interest in the context of this book, changes in the subject agent’s belief over the models and changes in the models themselves have to be included in the update. The latter changes reflect the other’s observations and, if it is modeled intentionally, the update of the other agent’s beliefs is the result of its actions and observations. In this case, the agent has to update its beliefs about the other agent based on which models support its observations and on what it anticipates the other agent may observe and how it updates.

To facilitate understanding, we may decompose the belief update, denoted using , into the two steps of prediction and correction, analogously to POMDPs. Gmytrasiewicz and Doshi [22] provide a formal derivation of the update from first principles. In the first step (Eq. 8.1), the distribution over the interactive state is updated given the joint action of the agents and the previous belief. We predict the probability of the other agent’s action using its models and revise its intentional models by updating the belief contained in each of them using the action and its possible observations:

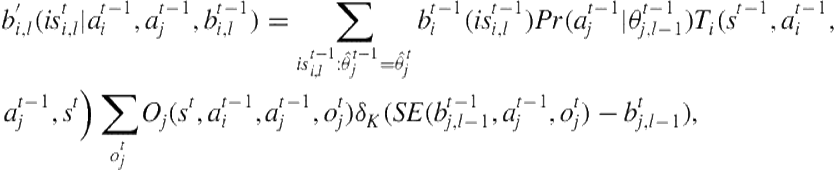(8.1)

where

is the distribution over ’s actions obtained by solving the intentional model.

is the Kronecker delta function, which is 1 when its argument vanishes and 0 otherwise.

is the update of the other agent’s belief in its model, .

The rest of the functions were defined previously.

Because the other agent’s action is not directly observed, beliefs obtained after prediction are averaged over the other agent’s action and weighted based on the likelihood of the observation, , that receives:

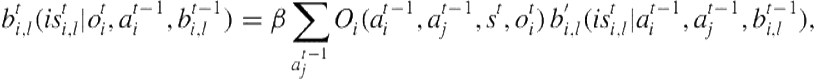(8.2)

where

is the normalization constant.

is defined in Eq. 8.1.

is as defined previously.

While the belief update just presented is for intentional models, it is performed analogously when the model is subintentional, with the main difference being that ’s belief and its update are not explicitly considered. Equations 8.1 and 8.2 together formalize a key inferential step of modeling others within the belief update. This involves updating the subject agent’s belief over the models and updating the models themselves, both of which facilitate dynamic plan recognition under uncertainty.

8.2.3 Solution Using Value Iteration

Analogous to a POMDP, we associate a value with each belief, which represents the discounted, long-term expected reward that would be obtained by starting at that belief and following the optimal policy from there onward. Formally,

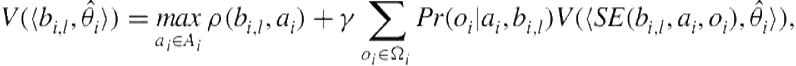
where and discounts the value of the future expected reward. Because the belief space is continuous, we may not iteratively compute the value of each belief. Instead, we compute the value of each interactive state (i.e., corners of the belief simplex) and obtain the value for each belief by performing an inner product between the vector of values for the interactive states and the belief vector. However, notice that the space of interactive states itself may be very large but is countable¹ and may be abstracted to permit solutions [39].

While the asymptotic complexity of finitely nested I-POMDPs has not been formally established as yet, it is possible that they are at least as difficult to solve as decentralized POMDPs. In particular, they may involve solving an exponential number of POMDPs with given beliefs, in the worst case.

8.3 Modeling Deep, Strategic Reasoning by Humans Using I-POMDPs

A general approach for recognizing the intent and plans of another agent in strategic contexts involves modeling its strategic reasoning. An important aspect of strategic reasoning is the depth to which one thinks about others’ thinking about others in order to decide on an action. Investigations in the context of human recursive reasoning [9,17,26,45] reveal a pessimistic outlook: in general-sum games, humans think about others’ strategies but usually do not ascribe further recursive thinking to others. When humans repeatedly experience games where others do reason about others’ actions to decide on their own, humans learn to reason about others’ reasoning; however, the learning in general tends to be slow, requiring many experiences, and incomplete—a significant population continues to exhibit shallow thinking.

Recently though, Goodie et al. [23] reported that in fixed-sum, competitive games human behavior is generally consistent with deeper levels of recursive reasoning. In games designed to test two and three levels of recursive reasoning, the observed actions were broadly consistent with the deeper levels by default. On experiencing these games repeatedly, the proportion of participants exhibiting the deeper thinking, leading to rational behavior in those games, increased even further, which is indicative of learning.

We apply I-POMDPs to model human judgment and behavioral data, reported by Goodie et al. [23], that is consistent with three levels of recursive reasoning in the context of fixed-sum games. In doing so, we investigate principled modeling of aggregate behavioral data consistent with levels rarely observed before and provide insights on how humans model another’s planning. Previously, Doshi et al. [15] used an empirically informed I-POMDP, simplified and augmented with psychologically plausible learning and choice models, to computationally model data pertaining to recursive reasoning up to the second level. Data from both general- and fixed-sum games, providing evidence of predominantly level 1 and 2 reasoning, respectively, were successfully modeled.

An I-POMDP is particularly appropriate because of its use of intentional modeling, which elegantly integrates modeling others and others’ modeling of others in the subject agent’s decision-making process. Furthermore, intentional models are directly amenable to descriptively modeling human behavior. An important outcome of this application of I-POMDPs is that it contributes specific insights on how people perform plan recognition in strategic contexts involving extended interactions.

We investigate the performance of three candidate models on previously unmodeled behavioral data. Our first model is the previous I-POMDP-based model, which uses underweighted belief learning, parameterized by , and a quantal-response choice model[31] for the subject agent, parameterized by . This choice model is based on the broad empirical finding that rather than always choosing the optimal action that maximizes the expected utility, individuals are known to select actions that are proportional to their utilities. The quantal-response model assigns a probability of choosing an action as a sigmoidal function of how close to optimal is the action:

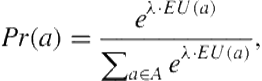(8.3)

where is an action of the subject agent belonging to the set, , and is the expected utility of this action. Choice models (e.g., the quantal response), which permit multiple actions, serve a dual purpose of allowing for choices that reasoning may not have modeled accurately. We extend the I-POMDP-based model to make it applicable to games, evaluating up to level 3 reasoning.

Although the preceding model employs an empirically supported choice model for the subject agent, it does not ascribe plausible choice models to the opponent in the experiments who is also projected as being human. We hypothesize that an informed-choice model for the opponent supports more nuanced explanations for observed opponent actions. This provides greater flexibility to the model, thereby leading to improved performance. Thus, our second candidate model generalizes the previous by intuitively using a quantal-response choice model for selecting the opponent’s actions at level 2.

Finally, our third candidate model deviates from using I-POMDPs by using weighted fictitious play [12], which predominantly relies on the past pattern of the opponent’s observed actions to form a judgment about what the opponent will do next. We couple it with a quantal-response choice model to generate the decisions for the games. This model differs from the previous two in that it does not seek to ascertain the mental models of the opponent but instead bases itself on the observed frequency of empirical play.

Other decision–theoretic approaches exist that model reasoning about others. A Bayesian model [3,24] attributes representational beliefs and desires to others; it captures these attributions as Bayesian inference in a POMDP that does rational planning and belief updating. Baker et al. [3] employed this approach in controlled spatial scenarios to infer participants’ judgment about the initial beliefs and desires of another agent from observed data. In particular, the experiments demonstrated that the full representational capacity of POMDPs was needed to explain human judgments about both beliefs and desires of others, which may change in the scenarios.

PsychSim [38], a social simulation tool, employs a formal decision–theoretic approach using recursive modeling to provide a computational model of how agents influence each other’s beliefs. PsychSim was used to analyze toy school bully scenarios and deployed in training software for teaching cross-cultural skills (e.g., language and negotiation) for modeling urban stabilization and health interventions. Another POMDP-based model [40] used beliefs based on the well-known cognitive hierarchy [9] combined with an inequity-aversion-based utility function, leading to a generative model to classify different types of subjects engaged in multiround investor–trustee games. In these studies, belief attributions play a key role in the modeling of reasoning about others’ actions in the context of human social interactions. Similarly, beliefs generalized recursively are integral to I-POMDPs and our modeling of data.

8.3.1 Background: Level 3 Recursive Reasoning

The experiments used a two-player, alternate-move game of complete and perfect information. The game and its tree are depicted in Figure 8.1. It starts at state A, where player may choose to move or stay. If chooses to move, the game goes to state B, where player needs to decide between moving or staying. If a move is taken, the game proceeds to the next state and the other player takes her or his turn to choose. The game continues up to two moves of . An action of stay by either player also terminates the game. In the study, the focus is on how player plays the game when it starts at A.

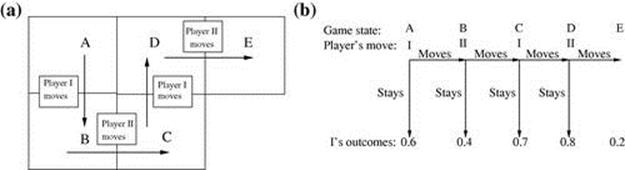
FIGURE 8.1 A four-stage, fixed-sum sequential game in (a) grid and (b) tree form. The probabilities are for player I. While the structure is similar to Rosenthal’s Centipede game [41], the fixed-sum payoffs differ. The sum of the players’ payoffs in Rosenthal’s version grow as the game progresses (“the pie grows”); they remain fixed at 1 in this game.

Outcomes of staying or when the game terminates at E are probabilities of winning in a different task for each player. The rational action is the one that maximizes the probability of winning. To decide whether to move or stay at state A, a rational player must reason about whether player will choose to move or stay at B. A rational player ’s choice in turn depends on whether player will move or stay at C, and a rational player ’s choice in turn depends on whether player will move or stay at D. Thus, the game lends itself naturally to recursive reasoning, and the level of reasoning is governed by the height of the game tree.

8.3.1.1 Methodology

To test up to the third level of recursive reasoning, Goodie et al. designed the computer opponent (player ), projected as a human player, to play a game in three ways if player chooses to move and the game proceeds to state B:

1. Player decides on an action by simply choosing rationally between the outcomes of default staying at states B and C in Figure 8.1; is a zero-level player and is called myopic.

2. reasons that player will choose rationally between the outcomes of stay at C and move followed by default stay at D, and based on this action, selects an action that maximizes its outcomes; is a first-level player who explicitly reasons about ’s subsequent choice and is called predictive.

3. reasons that player is predictive and will act rationally at C, reasoning about ’s rational action at D; is a second-level player who explicitly reasons about ’s subsequent choice, which is decided by rationally thinking about ’s subsequent action at D. We call this type of a super-predictive.

Therefore, if player thinks that II is super-predictive, then is reasoning extensively to the third level.

To illustrate, if player in Figure 8.1 chooses to move, then she thinks that a myopic player will stay to obtain a payoff of 0.6 at B compared to move, which will obtain 0.3 at C. She thinks that a predictive thinking that being myopic will move to D, thereby obtaining 0.8 instead of staying at C, and will decide to move, thinking that he can later move from D to E, which gives an outcome of 0.8. A super-predictive knows that is predictive, expecting that if moves from C to D then will move to E, which gives only 0.2; thus, will choose to stay at C and, therefore, will stay at B.

The rational choice of players depends on the preferential ordering of states of the game rather than specific probabilities. Because we cannot find a single preference ordering that distinguishes between the actions of the three opponent reasoning types, Goodie et al. [23] employed a combination of two differently ordered games to diagnose each level of reasoning from the other two.

8.3.1.2 Results

Participants were assigned randomly to different groups that played against a myopic, predictive, or super-predictive opponent. Each person participated in 30 trials, with each trial consisting of two games with payoff orderings that were diagnostic and a “catch” trial controlling for inattention. For convenience of presentation, the 30 trials were grouped into 6 blocks of 5 trials each.

From the participants’ data in each of the three types of opponent groups, Goodie et al. measured an achievement score, which is the proportion of trials in a block in which the participants played the conditionally rational action (best response) given the opponent’s level of reasoning. They also reported a prediction score, which is the proportion of trials in which the participants’ expectation about the opponent’s action was correct given the opponent type. This score provides a measure of successful plan recognition. The rationality error measured the proportion of trials in which participants’ actions were not consistent with their expectations of the opponent’s actions.

In Figure 8.2(a), we show the mean achievement scores across all participants for each of the three opponent groups. Goodie et al. define a metric, L, as the trial after which performance over the most recent 10 trials never failed to achieve statistical significance (cumulative binomial probability < 0.05). This implies making no more than one incorrect choice in any window of 10 trials. For participants who never permanently achieved statistical significance, L was assigned a value of 30. We observe that participants in the super-predictive opponent group had the highest overall achievement score, with an average L score of 11.3, followed by those in myopic opponent group with L score of 27.2. These L scores are consistent with the observations that achievement scores in these two groups are increasing.

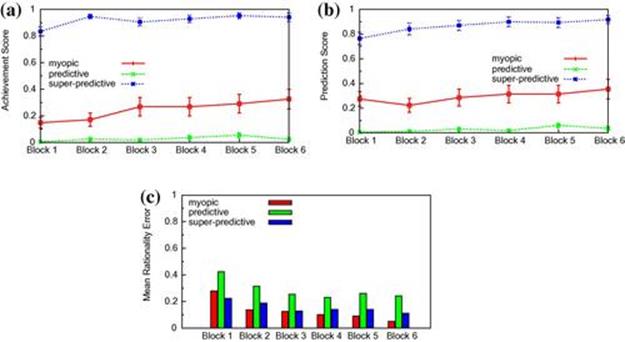
FIGURE 8.2 (a) Mean achievement and (b) mean prediction scores of participants for the different opponent groups across test blocks. (c) Mean rationality errors. Comparatively low achievement scores for the myopic opponent group are due to a large proportion of participants in that group reasoning at the deepest level of 3, but this proportion gradually reduces due to learning.

We further investigated the achievement scores for the myopic opponent group by computing the mean achievement scores for just this group given the three types of opponents. We observed that the achievement scores of this group, given a super-predictive opponent, are high, indicating that a large proportion of participants are reasoning at the deepest level of 3; however, this proportion gradually reduces as a result of learning. Participants in the predictive opponent group had an achievement score close to 0 and an L score of 30, which means they never truly achieved a corresponding strategy. Similar to the mean achievement score, participants in the super-predictive opponent group exhibited the highest prediction scores while those in the predictive opponent group had the lowest scores; see Figure 8.2(b).

The high achievement scores for the super-predictive group in combination with the low achievement scores for the other groups validate the study’s hypothesis that participants generally engage in third-level reasoning by default in enabling scenarios. A secondary hypothesis was that participants’ reasoning level will change from the default as the games progress. This is evident from the significantly increasing achievement scores for the super-predictive and myopic groups, thereby providing evidence of learning. However, participants for whom first-level reasoning is optimal learned slowly and incompletely.

8.3.2 Computational Modeling

We seek process-oriented and principled computational models with predictions that are consistent with the observed data of the previous subsection. These models differ from statistical curve fitting by providing some insights into the cognitive processes of judgment and decision making that possibly led to the observed data. To computationally model the results, a multiagent framework that integrates recursive reasoning in the decision process is needed. Finitely nested I-POMDPs described in Section 8.2 represent a choice that meets the requirements of explicit consideration of recursive beliefs and decision making based on such beliefs.

8.3.2.1 Simplified and empirically informed I-POMDP

Doshi et al. [15] modeled the shorter three-stage games using . We extend this modeling to the four-stage games considered here. These games challenge modeling by being larger; allow for a deeper level of reasoning; and, as mentioned in Section 8.3.1, permit additional plausible models that could be ascribed to the opponent. As Doshi et al. noted, the lookahead in the game is naturally modeled recursively rather than sequentially, and we model the four-stage game using .

Physical state space, , is perfectly observable though the interactive space is not; ’s actions, are deterministic and has similar actions; observes other’s actions, is not needed; deterministically indicates ’s action given ’s observations; and captures the diagnostic preferential ordering of the states contingent on which of the three games in a trial is being considered.

Because the opponent is thought to be human and guided by payoffs, we focus on intentional models only. Given that expectations about the opponent’s action by the participants showed consistency with the opponent types used in the experimentation, intuitively, model set , where is the level 0 (myopic) model of the opponent, is the level 1 (predictive) model, and is the level 2 (super-predictive) model—all of which model ’s action at the superscripted state B. Parameters of these models are analogous to the I-POMDP for agent , except for , which reflects the preferential ordering of the states for the opponent.

The super-predictive model, , includes the level 1 model of , which includes the level 0 model of , in its interactive state space. Agent ’s initial belief, , assigns a probability distribution to ’s models based on the game being modeled. This belief will reflect the general, de facto thinking of the participants about their opponents. It also assigns a marginal probability 1 to state A, indicating that decides at that state. Beliefs that are part of ’s three models, respectively, assign a marginal probability 1 to B, indicating that acts at that state. Belief , which is part of , assigns a probability of 1 to state C. Additionally, belief , which is part of , assigns a marginal probability of 1 to state D.

Previous investigations of strategic behavior in games, including Trust [29] and Rosenthal’s Centipede games, have attributed social models (e.g., reciprocity and altruistic behavior) to others [18,32,40]. Although it may not be possible to completely eliminate such social factors and others (e.g., inequality aversion) from influencing participants’ choices, Goodie et al. sought to design the game to minimize their effects and isolate the level of recursive thinking as the variable. Reciprocity motivates participants to reward kind actions and punish unkind ones.

Altruism and reciprocity are usually observed when the sum of payoffs for both players has a potential to increase through altruistic actions, as in both the Trust and Rosenthal’s Centipede games. However, the setting of fixed-sum with no increase in total payoffs at any stage makes the games we consider competitive and discourages these models. Nevertheless, participants may choose to alternate between staying and providing an opportunity to the opponent by moving at state A. Such play is weakly reflective of altruism and is also optimal given the opponent types of myopic and predictive in our games. Consequently, it should result in high achievement scores for these groups. Figure 8.2 shows low achievement scores for these groups and high achievement scores for the super-predictive group that requires the participant to stay at each game, both of which point to minimal evidence of such alternating play.

Another social process that could explain some of the participants’ behavior is a desire for inequality aversion [16], which would motivate participants to choose an action that leads to similar chances of winning for both players. For example, such a desire should cause participants to move proportionately more if the chance of winning at state A is 0.6 and this chance is preferentially in the middle, than say, when the chance at A is between 0.45 and 0.55. However, participants displayed a lower move rate of about 12% in the former case compared to a move rate of 14.5% in the latter case. Thus, we believe that inequality aversion did not play a significant role in motivating participants, and we do not model it. Finally, Goodie et al. [23] report on an additional experiment, which measured for the effect of uncertainty (risk) aversion on choices, and concluded that it did not offer an alternative explanation for the observed data.

8.3.2.2 Learning and decision models

From Figures 8.2(a,b) and our analysis, notice that some of the participants learn about the opponent model as they continue to play. However, in general, the rate of learning is slow. This is indicative of the cognitive phenomenon that the participants could be underweighting the evidence they observe. We may model this by making the observations slightly noisy in and augmenting normative Bayesian learning in the following way:

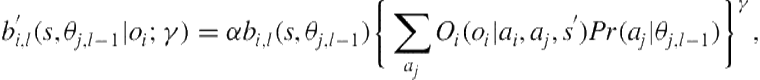(8.4)

where is the normalization factor; is the nested level of the model; state corresponds to A and to B; action is to move; and if , then the evidence is underweighted while updating the belief over ’s models.

In Figure 8.2(c), we observe significant rationality errors in the participants’ decision making. Such “noisy” play was also observed by McKelvey and Palfrey [32] and included in the model for their data. We use the quantal-response model [31] described previously in Eq. 8.3 to simulate human nonnormative choice. Although the quantal response has broad empirical support, it may not correctly model the reasons behind nonnormative choice in this context. Nevertheless, its inclusive property provides our modeling with a general capability to account for observed actions that are not rational.

Doshi et al. [15] augmented I-POMDPs with both these models to simulate human recursive reasoning up to level 2. As they continue to apply to our data, we extend the I-POMDP model to the longer games and label it as .

The methodology for the experiments reveals that the participants are deceived into thinking that the opponent is human. Therefore, participants may justify observed actions of the opponent that are not rational given the attributed type as errors in their decision making rather than due to their level of reasoning. Thus, we generalize the previous model by attributing quantal-response choice to opponent’s action selection as well. We clarify that our use of quantal response here provides a way for our model to account for nonnormative choices by others. Let be the quantal-response parameter for the participant and be the parameter for the opponent’s action. Then,

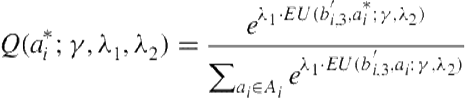(8.5)

parameters, is the participant’s action and is the probability assigned by the model. is the expected utility for on performing action , given its updated belief, , for the game, with parameterizing ’s action probabilities, , present in Eq. 8.4 and in computation of the utility. We label this new model as .

8.3.2.3 Weighted fictitious play

A different reason for participant behavior that relies more heavily on past patterns of observed actions of the opponent, instead of ascertaining the mental models of the opponent as in the previous I-POMDP-based models, is applicable. A well-known learning model in this regard is weighted (generalized) fictitious play [12]. To apply this model, we first transform the game of Figure 8.1 into its equivalent normal form.

Let be the observed frequency of opponent’s action, . We update this as:

(8.6)

where parameter is the weight put on the past observations; is an indicator function that is 1 when ’s action in consideration is identical to the currently observed ’s action, , and 0 otherwise. We point out that when , the model collapses into the Cournot dynamics that involves responding to the opponent’s action in the previous time step only. When , it assumes the form of the original fictitious play. We may initialize to 1 for all actions. The weighted frequency, when normalized, is deemed to be representative of agent ’s belief of what will do in the next game in the trials.

Due to the presence of rationality errors in the data, we combine the belief update of Eq. 8.6 with quantal response:

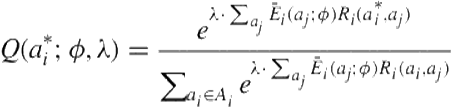(8.7)

Here, is the normalized frequency (belief) as obtained from Eq. 8.6 and . We label this model as .

8.3.3 Evaluation

We evaluate the comparative fitness of the different generative models to the data and visually compare the experiment’s data with model simulations. We begin by discussing our technique for learning the parameters of the models from the data.

8.3.3.1 Learning parameters from data

In , three parameters are involved: representing participants’ learning rate, representing nonnormative actions of the participant and her opponent, respectively. The empirically informed I-POMDP model gives a likelihood of the experiment data given specific values of the three parameters.

We begin by learning . Because this parameter characterizes expected opponent behavior, we use the participants’ expectations of their opponent’s action in each game, denoted as , as the data. Denoting this set of expectations as , the likelihood of is obtained by taking the product of over games and participants because the probability is hypothesized to be conditionally independent between games given the model and is independent between participants.

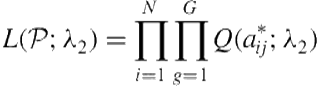
Here, is the observed expectation of ’s action in game , and is the probability assigned by the model to the action, with a computation that is analogous to Eq. 8.5 except that ’s lower-level belief replaces ’s belief and does not ascribe nonnormative choice to its opponent.

To learn parameters (or in ), we use the participants’ actions at state A. Data consisting of these actions are denoted as . The likelihood of this data is given by the probability of the observed actions of participant as assigned by our model over all games and participants.

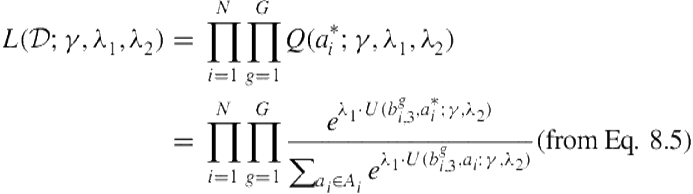
We may simplify the computation of the likelihoods by taking its log. To estimate the values of the three parameters (), we maximize the log likelihoods using the Nelder–Mead simplex method [36]. Notice that the ideal functions will assign a probability of 1 to the observed actions, resulting in a log likelihood of 0; otherwise, the likelihoods are negative.

Parameters for are learned by maximizing the log likelihood of the data, , in which the quantal-response function is as shown in Eq. 8.7. In this regard, we note that the experiment’s data include actions performed by the participants at states A and C, and programmed opponent actions at states B and D, if the game progressed to those states.

8.3.3.2 Model performance

We use stratified, fivefold cross-validation to learn the parameters and evaluate the models.

To learn , we use the expectations data of the catch games only. This is because no matter the type of the opponent, the rational action for the opponent in catch games is to move. Thus, expectations of stay by the participants in the catch trials would signal a nonnormative action selection by the opponent. This also permits learning a single value across the three groups. However, this is not the case for the other parameters.

In Figure 8.2, we observe that for different opponents, the learning rate, L, is different. Also, in Figure 8.2(c), we observe that the rationality errors differ considerably between the opponent groups. Therefore, we learn parameters, and given the value of (and in ), separately from each group’s diagnostic games. Analogously, we learn and for from the diagnostic games. We report the learned parameters averaged over the training folds in Table 8.1.

Table 8.1

Average Parameter Values Learned from the Training Folds

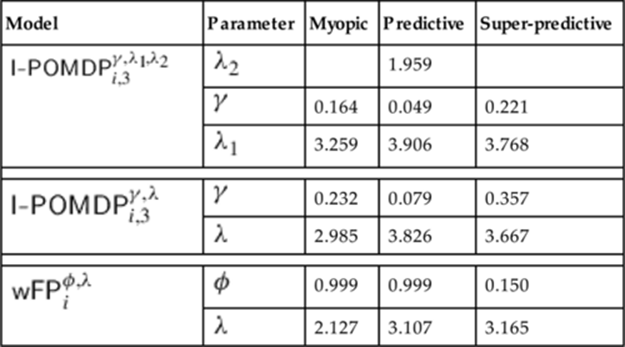
Note: Data for the experiment are for the three candidate models.

From Table 8.1, we see that for the predictive opponent group is close to 0. This is consistent with the observation that participants in this group did not make much progress in learning the opponent’s type. Consequently, we focus our analysis on the myopic and super-predictive opponent groups from here onward. Furthermore, note the dichotomy in the value of between the myopic and super-predictive opponent groups. A value closer to 0 for the super-predictive group indicates that the previously observed action is mostly sufficient to predict the opponent’s action in the next game. However, ’s value close to 1 is indicative of the past pattern of observed actions, not helping much in modeling the behavior of the other groups.

We show the log likelihoods of the different models, including a random one that predicts the other’s actions randomly and chooses its own actions randomly, in Table 8.2. The random model serves as our null hypothesis. We point out that has the highest likelihood in the myopic context, although the likelihood of the other I-POMDP-based model is slightly better for the super-predictive group. The difference for the myopic context is significant, with a log likelihood ratio test yielding , while the difference for the super-predictive context is not significant.

Table 8.2

Log Likelihood of the Different Models Evaluated on the Test Folds

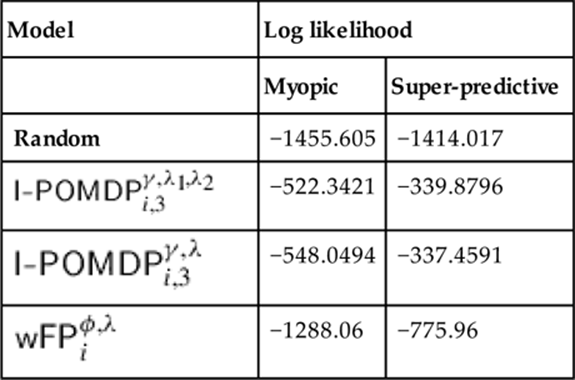
Note: This table uses the parameters shown in Table 8.1. The difference between the I-POMDP-based models for the myopic group is significant.

On the other hand, exhibits a vast difference in the log likelihoods between groups, with the low likelihood for the myopic group—though still better than that for the random model—indicating a poor fit. As we see next, this is a result of the potentially poor descriptive prediction of the opponent’s actions by relying solely on observed empirical play.

We use the learned values in Table 8.1 to parameterize the underweighting and quantal responses within the I-POMDP-based models and fictitious play. We cross-validated the models on the test folds. Using a participant’s actions in the first 5 trials, we initialized the prior belief distribution over the opponent types. The average simulation performance of the model is displayed in Figure 8.3. We do not show the simulation performance of other models due to lack of space. Notice that -based achievement and prediction scores have values and trends similar to the experimental data. However, there is some discrepancy in the first block caused by the difficulty in determining an accurate measure of the participant’s initial beliefs as she or he starts the experiment. Each model data point is the average of 500 simulation runs.

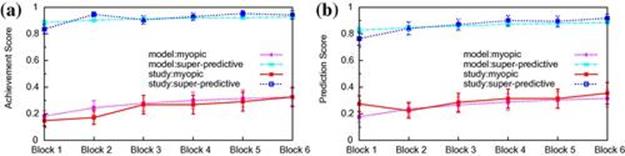
FIGURE 8.3 Comparison of -based Simulations with Actual Data in Test Folds (a) mean achievement scores and (b) mean prediction scores. The model-based scores exhibit values and trends similar to the experimental data, albeit the larger discrepancy in the first block. Additionally, the trend in the model-based scores appears smoother compared to the actual data, possibly because of the large number of simulation runs.

We also measure the goodness of the fit by computing the mean squared error (MSE) of the output by the models—, and —and compare it to those of the random model (null hypothesis) for significance. We show the MSE for the achievement and prediction scores based on the models in Table 8.3.

Table 8.3

MSE of the Different Models Comparison with the Experiment’s Data

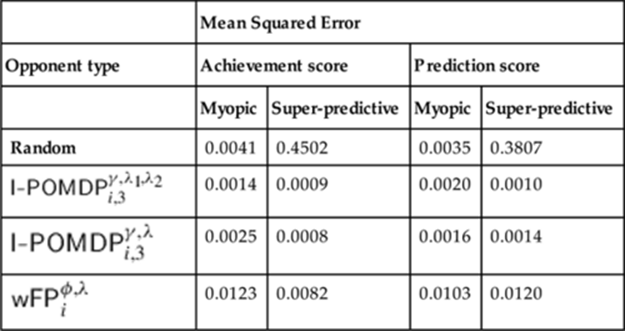
Note: The difference in MSE of the achievement score for the myopic group between the two I-POMDP models is significant.

Notice from the table that both I-POMDP-based models have MSEs that are significantly lower than the random model. Recall that the log likelihood of is higher than for the myopic opponent (refer to Table 8.2). This is reflected in the difference in MSE of the achievement score for the myopic group between the two that is significant (Student’s paired t-test: ). However, other MSE differences between the two models are insignificant and do not distinguish one model over the other across the scores and groups. A large MSE of reflects its weak simulation performance, although it does improve on the par set by random model for the super-predictive group.

Although attributing nonnormative action selection to the opponent did not result in significantly more accurate expectations for any group, we think that it allowed the model to generate actions for agent that fit the data better by supporting an additional account of ’s (surprising) myopic behavior. This provides preliminary evidence that humans could be attributing the same error in choice that they themselves make to others. Of course, this positive result should be placed in the context of the increased expense of learning an additional parameter, .

8.4 Discussion

Recent applications of I-POMDPs testify to the significance and growing appeal of intent-recognition and decision–theoretic planning in multiagent settings. They are being used to explore strategies for countering money laundering by terrorists [34,37] and enhanced to include trust levels for facilitating defense simulations [42,43]. They have been used to produce winning strategies for playing the lemonade stand game [47], explored for use in playing Kriegspiel [20,21], and even discussed as a suitable framework for a robot learning a task interactively from a human teacher [46].

Real-world applications of planning often involve mixed settings populated by humans and human-controlled agents. Examples of such applications include UAV reconnaissance in an urban operating theater and online negotiations involving humans. The optimality of an agent’s decisions as prescribed by frameworks, such as I-POMDPs, in these settings depends on how accurately the agent models the strategic reasoning of others and, subsequently, on their plans. Consequently, I-POMDPs have been modified to include empirical models for simulating human behavioral data pertaining to strategic thought and action [15], an application that we explored in detail earlier in this chapter. Successfully modeling deep-recursive reasoning is indicative that multiagent decision–theoretic models can be descriptively expressive and can provide a principled alternative to ad hoc modeling.

Additionally, parameterized and procedural modeling contributes valuable insights on how people engage in recognizing others’ strategic plans. For example, the substantial mean prediction scores observed for the super-predictive and myopic groups (refer toFigure 8.2) imply that participants in our context generally predict that others are using the optimal strategy and—with less success—the simple strategy of relying on just immediate rewards. This implies that people are capable of thorough thinking about others’ plans in motivating scenarios. As they experience more games, which provides an opportunity for learning others’ plans, the general level of success improves, though slowly, and remains incomplete. Finally, the modeling points toward people attributing the possibility of nonnormative action selection to others.

Although the simplicity of our particular game setting did not require the full use of the I-POMDP machinery, it does provide a principled “top-down” point of departure for building computational models. Of course, the alternative would be to build new models from scratch, “bottom-up,” which may not generalize. I-POMDPs bring with themselves a probabilistic representation and belief-based learning, both of which are key to this behavioral modeling application. Even though we did not show modeling results for the predictive opponent group in order to promote clarity, the I-POMDP-based models simulated the low scores closely.

Despite the good descriptive validity, I-POMDP models should not be viewed as being uniquely competent for modeling data. Nor should they preclude exploring opponent modeling along different dimensions. For example, our use of the quantal-response choice model characterizes the probability of selecting actions as being proportional to their expected utilities. While this model is indeed plausible, a simpler choice model, which suggests performing the optimal action with probability and uniformly distributed over the remaining actions, could be plausible as well.

As applications emerge for I-POMDPs, approaches that allow their solutions to scale become crucial. Consequently, developing approximations that trade solution optimality for efficiency is a fruitful line of investigation for decision–theoretic planning in multiagent settings.

8.5 Conclusion

Decision-theoretic planning in multiagent settings as formalized using the I-POMDP framework combines inferential reasoning over agent models with decision-theoretic planning in partially observable environments. If the models are intentional, reasoning on a nested hierarchy of models is performed. We explored an application of this framework appropriately generalized with cognitive models of choice and belief update toward modeling behavioral data on human recursive thinking in competitive games. Empirical results demonstrate that humans could be attributing the same errors in choice that they themselves make to others in order to explain non-normative behavior of others. This finding improves our understanding of the theory of mind and adversarial intent.

References

1. Aumann RJ, Brandenburger A. Epistemic conditions for Nash equilibirum. Econometrica. 1995;63:1161-1180.

2. Aumann RJ. Interactive epistemology II: probability. Int J Game Theor. 1999;28:301-314.

3. Baker C, Saxe R, Tenenbaum J. Bayesian theory of mind: modeling joint belief-desire attribution. Conference of Cognitive Science Society. 2011:2469-2474.

4. Bernstein DS, Givan R, Immerman N, Zilberstein S. The complexity of decentralized control of Markov decision processes. Math Oper Res. 2002;27:819-840.

5. Binmore K. Essays on foundations of game theory. Pittman; 1982.

6. Brandenburger A. The power of paradox: some recent developments in interactive epistemology. Int J Game Theor. 2007;35:465-492.

7. Brandenburger A, Dekel E. Hierarchies of beliefs and common knowledge. J Economic Theor. 1993;59:189-198.

8. Camerer C. Behavioral game theory: experiments in strategic interaction. Princeton University Press; 2003.

9. Camerer C, Ho T-H, Chong J-K. A cognitive hierarchy model of games. Quart J Econom. 2004;119:861-898.

10. Charniak E, Goldman R. A probabilistic model for plan recognition. Proceedings AAAI. 1991:160-165.

11. Charniak E, Goldman R. A Bayesian model of plan recognition. Artifi Intell. 1993;64:53-79.

12. Cheung Y-W, Friedman D. Individual learning in normal-form games. Games Econom Behav. 1997;19:46-76.

13. Dennett D. Intentional systems. Brainstorms. MIT Press; 1986.

14. Doshi P. Decision making in complex multiagent settings: a tale of two frameworks. AI Mag. 2012;33:82-95.

15. Doshi P, Qu X, Goodie A, Young D. Modeling human recursive reasoning using empirically informed interactive POMDPs. IEEE Trans Syst Man Cybern A: Syst Humans. 2012;42(6):1529-1542.

16. Fehr E, Schmidt K. A theory of fairness, competition and cooperation. Quart J Econom. 1999;114:817-868.

17. Ficici S, Pfeffer A. Modeling how humans reason about others with partial information. International Conference on Autonomous Agents and Multiagent Systems. 2008:315-322.

18. Gal Y, Pfeffer A. Modeling reciprocal behavior in human bilateral negotiation. Twenty-Second Conference on Artificial Intelligence. 2007:815-820.

19. Geib CW, Goldman RP. Recognizing plan/goal abandonment. Eighteenth International Joint Conference on Artificial Intelligence. 2003:1515-1517.

20. Giudice AD, Gmytrasiewicz P. Towards strategic Kriegspiel play with opponent modeling. Game Theoretic and Decision-Theoretic Agents, AAAI Spring Symposium. 2007:17-22.

21. Giudice AD, Gmytrasiewicz P. Towards strategic Kriegspiel play with opponent modeling (extended abstract). Autonomous Agents and Multiagent Systems Conference. 2009:1265-1266.

22. Gmytrasiewicz PJ, Doshi P. A framework for sequential planning in multiagent settings. J Artif Intell Res. 2005;24:49-79.

23. Goodie AS, Doshi P, Young DL. Levels of theory-of-mind reasoning in competitive games. J Behav Decis Making. 2012;24:95-108.

24. Goodman N, Baker C, Tenebaum J. Cause and intent: social reasoning in causal learning. Conference of Cognitive Science Society. 2009:2759-2764.

25. Harsanyi JC. Games with incomplete information played by Bayesian players. Manage Sci. 1967;14:159-182.

26. Hedden T, Zhang J. What do you think I think you think? Strategic reasoning in matrix games. Cognition. 2002;85:1-36.

27. Hoffmann J, Brafman RI. Contingent planning via heuristic forward search with implicit belief states. International Conference on Artificial Planning Systems. 2005:71-80.

28. Kaelbling L, Littman M, Cassandra A. Planning and acting in partially observable stochastic domains. Artif Intell. 1998;101:99-134.

29. King-Casas B, Tomlin D, Anen C, Camerer C, Quartz S, Montague P. Getting to know you: reputation and trust in a two-person economic exchange. Science. 2005;308:78-83.

30. Littman M. A tutorial on partially observable Markov decision processes. J Math Psychol. 2009;53:119-125.

31. McKelvey R, Palfrey T. Quantal response equilibria for normal form games. Games Econom Behav. 1995;10:6-38.

32. McKelvey RD, Palfrey TR. An experimental study of the centipede game. Econometrica. 1992;60:803-836.

33. Meijering B, Rijn HV, Taatgen N, Verbrugge R. I do know what you think I think: second-order theory of mind in strategic games is not that difficult. Cognitive Science. 2011:2486-2491.

34. Meissner C. A complex game of cat and mouse. Lawrence Livermore Natl Labor Sci Technol Rev. 2011:18-21.

35. Mertens J, Zamir S. Formulation of Bayesian analysis for games with incomplete information. Int J Game Theor. 1985;14:1-29.

36. Nelder JA, Mead R. A simplex method for function minimization. Comput J. 1965;7:308-313.

37. Ng B, Meyers C, Boakye K, Nitao J. Towards applying interactive POMDPs to real-world adversary modeling. Innovative Applications in Artificial Intelligence. 2010:1814-1820.

38. Pynadath D, Marsella S. Psychsim: modeling theory of mind with decision-theoretic agents. International Joint Conference on Artificial Intelligence. 2005:1181-1186.

39. Rathnasabapathy B, Doshi P, Gmytrasiewicz PJ. Exact solutions to interactive POMDPs using behavioral equivalence. Autonomous Agents and Multi-Agent Systems Conference. 2006:1025-1032.

40. Ray D, King-Casas B, Montague PR, Dayan P. Bayesian model of behavior in economic games. Neural information processing systems. 2008:1345-1352.

41. Rosenthal R. Games of perfect information, predatory pricing and the chain store paradox. J Econom Theor. 1981;25:92-100.

42. Seymour R, Peterson GL. Responding to sneaky agents in multi-agent domains. Florida Artificial Intelligence Research Society Conference. 2009:99-104.

43. Seymour R, Peterson GL. A trust-based multiagent system. IEEE International Conference on Computational Science and Engineering. 2009:109-116.

44. Smallwood R, Sondik E. The optimal control of partially observable Markov decision processes over a finite horizon. Oper Res. 1973;21:1071-1088.

45. Stahl D, Wilson P. On player’s models of other players: theory and experimental evidence. Games Econom Behav. 1995;10:218-254.

46. Woodward, MP, Wood, RJ. Learning from humans as an I-POMDP. Position paper, Harvard University; 2010.

47. Wunder M, Kaisers M, Yaros J, Littman M. Using iterated reasoning to predict opponent strategies. International Conference on Autonomous Agents and Multi-Agent Systems. 2011:593-600.