Modeling Human Plan Recognition Using Bayesian Theory of Mind - Modeling Human Cognition - Plan, Activity, and Intent Recognition: Theory and Practice, FIRST EDITION (2014)

Plan, Activity, and Intent Recognition: Theory and Practice, FIRST EDITION (2014)

Part III. Modeling Human Cognition

Chapter 7. Modeling Human Plan Recognition Using Bayesian Theory of Mind

Chris L. Baker and Joshua B. Tenenbaum, Massachusetts Institute of Technology, Cambridge, MA, USA

Abstract

The human brain is the most powerful plan-recognition system we know. Central to the brain’s remarkable plan-recognition capacity is a theory of mind (ToM): our intuitive conception of other agents’ mental states—chiefly, beliefs and desires—and how they cause behavior. We present a Bayesian framework for ToM-based plan recognition, expressing generative models of belief- and desire-dependent planning in terms of partially observable Markov decision processes (POMDPs), and reconstructing an agent’s joint belief state and reward function using Bayesian inference, conditioned on observations of the agent’s behavior in the context of its environment. We show that the framework predicts human judgments with surprising accuracy, and substantially better than alternative accounts. We propose that “reverse engineering” human ToM by quantitatively evaluating the performance of computational cognitive models against data from human behavioral experiments provides a promising avenue for building plan recognition systems.

Keywords

theory of mind

commonsense psychology

belief–desire inference

cognitive modeling

Bayesian modeling

partially observable Markov decision processes

7.1 Introduction

Among the many impressive cognitive endowments of the human species, our physical intelligence and our social intelligence are two of the most essential for our success. Human physical intelligence uses intuitive theories of the physical laws of the world to maintain accurate representations of the state of the environment; analogously, human social intelligence uses folk–psychological theories to reason about other agents’ state of mind. For example, to drive safely we must reason about the acceleration and deceleration of massive objects (physical intelligence), but more subtly, we must reason about the state of mind of other drivers (social intelligence). Consider the situation in Figure 7.1, in which an oncoming car is approaching an intersection with its left turn signal on. To safely pass through this intersection in the opposite direction, a driver must quickly judge whether the driver of the oncoming car knows he is there. If yes, he can safely proceed through the intersection without slowing; if not, he should slow down to avoid a collision as the other car turns left in front of him. That these judgments go beyond simple, programmatic rules of thumb (e.g., “use caution at two-way intersections when oncoming car signals left”) is evident from the flexibility with which they apply. If eye contact is made with the oncoming driver, one can be more certain that she will wait; if there is glare on the windshield, the opposite is the case. Other contexts engage analogous cognitive processes; for example, there is always the risk that an oncoming car will turn left without signaling, which is more likely when the driver is on the phone, when visibility is poor, at intersections where left turns are prohibited and so on.

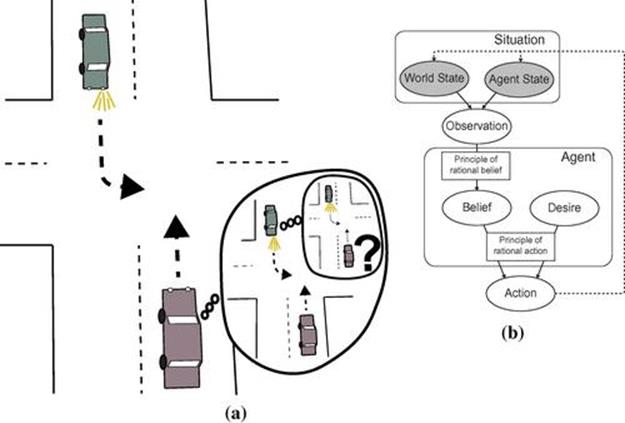
image

FIGURE 7.1 Commonsense theory of mind reasoning.(a) Safely crossing an intersection opposite a car signaling left requires us to represent the other driver’s beliefs about the situation: Does the driver of the oncoming car believe the way is clear? (b) Causal schema for ToM. Traditional accounts of ToM (e.g., Dennett [38], Wellman[136], and Gopnik and Meltzoff [57]) have proposed informal versions of this schema, characterizing the content and causal relations of ToM in commonsense terms; e.g., “seeing is believing” for the principle of rational belief, or “get what you desire” for the principle of rational action.

These kinds of nuanced, context-sensitive inferences are ubiquitous in human social intelligence, but virtually absent from even the most advanced artificial intelligence (AI) and robotic systems. To return to our driving example, the recent successes in self-driving cars [127], though impressive, are more the result of advances in machine vision and AI planning than social intelligence; even the most advanced, lifelike robots cannot reason about the beliefs, desires, and intentions of other agents. Machines lack a theory of mind (ToM): the intuitive grasp that humans have of our own and other people’s mental states—how they are structured, how they relate to the world, and how they cause behavior. Humans understand that others use their observations to maintain accurate representations of the state and structure of the world; that they have desires for the world to be a certain way; and that these mental states guide their actions in predictable ways, favoring the means most likely to achieve their desires according to their beliefs.

An influential view among developmental psychologists and philosophers is that ToM is constructed around an intuitive causal schema, sketched in Figure 7.1(b), in which beliefs and desires generate actions via abstract causal laws [57,137,138,91]. These causal models allow us to perform mental simulations of others’ situation-dependent thought processes and actions, and also to reason backward to infer what others are thinking, given their behavior. A growing body of evidence has shown that simple forms of these representations are present even in young infants, who by 6 months of age have the capacity to attribute goals or desires on the basis of others’ reaching movements [142], or to infer whether one agent intends to help or hinder another based on their actions and the context in which they are performed [63]. These abilities rapidly increase in sophistication; by as early as 10 months of age, infants represent agents’ beliefs and use them to predict their behavior [90,99] and attribute goals to agents who act rationally in pursuit of those goals, but not to agents who act irrationally [50,35].

Based on this evidence, Gergely et al. [50] have proposed that infants’ precocious social reasoning abilities rely on an early-emerging version of the “intentional stance” [38]: the assumption that agents will have sensible beliefs about the world and their situation, and will act rationally to achieve their desires; these functional relationships are illustrated by the “principle of rational belief” and “principle of rational action” boxes in Figure 7.1(b), respectively. Although this perspective provides a unifying account of the developmental data, its insights are restricted to qualitative phenomena—it does not explain quantitative variation in human reasoning as a function of actions, situations, or prior expectations of plausible mental states. Furthermore, generating empirical predictions from nonformal accounts involves introspecting on our own intuitive psychological knowledge—a circular reliance on the very intuitions theories of ToM must ultimately explain.

To go beyond these limitations, we propose to “reverse-engineer” the core representations and mechanisms of human ToM using cognitively inspired computational modeling. This allows us to test competing hypotheses about the nature of human ToM by comparing the ability of computational models defined over different knowledge representations—different priors over the kinds of mental states and the relations among them—to quantitatively fit human judgments into controlled behavioral experiments. We ground our modeling within the large body of research on plan, activity, and intent recognition (PAIR) to highlight its potential to scale to real-world action understanding problems of the kind that solve humans effortlessly, an essential property that computational theories of human ToM must capture.

Our proposed framework, called Bayesian theory of mind (BToM), formalizes ToM as a theory-based Bayesian model [126]. BToM formalizes the core principles of human ToM proposed by classic accounts—that others’ behavior is generated by approximately rational belief- and desire1-dependent planning—in terms of maximization of expected gains and minimization of expected losses within partially observable Markov decision processes (POMDPs) [76]. This casts ToM as a kind of “intuitive economics”—a folk analog of utility theory used for understanding everyday behavior. Importantly, this does not assume that humans necessarily plan or act rationally in all circumstances. Rather, we tacitly expect others to behave rationally (or approximately so) in particular situations, and perform “explanation by rationalization” by attributing the mental states that make their behavior appear the most rational within the present context. For a given situational context, these principles are applied by running an approximate planning mechanism, which takes the situation and the agents’ hypothesized beliefs and desires as input and produces a probability distribution over actions as output. Today, many off-the-shelf software packages are available that can provide this planning mechanism within BToM for modestly sized problems.

Our knowledge of others’ mental states is fundamentally uncertain, both due to the inability to observe them directly and due to the unpredictability of how someone with a particular mental state will behave; many different mental states could produce the same action, and the same mental state could produce many different actions. The probabilistic, causal models generated by the planning mechanism within BToM capture these properties, supporting prediction of agents’ noisy behavior, given their beliefs and desires, but also the reverse—“inverting” models of planning to perform causal inference of beliefs and desires, given observed behavior. We express “inverse planning” as a Bayesian inference, scoring candidate belief–desire hypotheses by the probability they could have generated the observed behavior, weighted by the prior.

These probabilistic inferences are inspired by techniques long employed within the PAIR literature; however, PAIR research has primarily focused on inference of “motivational” states (e.g., desires, goals, intentions or plans), rather than “epistemic” states (e.g., beliefs or knowledge). Traditionally, PAIR models also have not embedded probabilistic representations of behavior within top-down theories of rational planning, though this is now changing in the field [103,107,108,40,39] and in the work we describe here. These aspects of BToM are inspired by classic philosophical and psychological accounts of human ToM. Explicit representation of a theory of utility–theoretic planning is the key to integrating these two sources of inspiration, and highlights the inextricable coupling of belief and desire attributions—expected utility is a function of both beliefs and desires, with beliefs modulating the degree to which different desires influence any particular decision. In most situations, other agents’ beliefs are only partially known (as in our driving example), but when inferred jointly with desires, they can often be plainly determined.

We describe an experimental paradigm designed to evoke quantitatively varying judgments in situations that reflect the naturalistic contexts in which ToM is commonly used. For this, we created a “foraging” scenario in which observers (human subjects and computational models) are given a birds-eye view of individual agents walking around a campus environment to eat lunch at one of several “food trucks” (see Figure 7.2). Agents can desire to eat at particular trucks, but be uncertain about the trucks’ locations, requiring careful consideration of where to walk based on these desires and beliefs. Over a number of trials, the task is to infer the agent’s degree of desire for each truck and belief about each truck’s location, based on observing a single trajectory. This induces a rich set of joint attributions, ranging from totally uncertain beliefs and ambivalent desires to sharply peaked beliefs and strongly ordered desires. We analyze the output of BToM, as well as several alternative models, when given the same time-series input presented to human subjects, then compare the fit of each model to the human data. Accurately predicting people’s judgments across all conditions is a challenging task, and it provides a strong basis for identifying the best model of human ToM knowledge and reasoning.

image

FIGURE 7.2 Example experimental scenario.The small sprite represents the location of the agent and the black trail with arrows superimposed records the agent’s movement history. Two shaded cells in opposite corners of the environment represent spots where trucks can park and each contains a different truck. The shaded area of each frame represents the area that is outside of the agent’s current view. This figure shows actual frames from an experimental stimulus. (For color version of this figure, the reader is referred to the online version of this chapter.)

The remainder of this chapter is organized as follows. First, Section 7.2 begins with an informal description of the BToM framework to convey the main intuitions behind our modeling, expressed in terms of the food-truck domain of our experiments for clarity. We then provide the formal, mathematical details of BToM. We also formulate several alternative models as simplified versions of the full belief–desire inference model; these serve to test the level of representational complexity necessary to capture human ToM reasoning. We then relate our models to proposals from the large literature on PAIR, and discuss the connections between AI and psychology that have been made within this field. Section 7.3 describes a domain and methodology for testing computational models of ToM behaviorally, showing the output of our models over a selection of key scenarios, then comparing these predictions with human behavioral judgments. Section 7.4 describes several extensions of the BToM modeling and experiments presented here to give a sense of the generality of our approach. We also discuss limitations of the framework, and open questions for future research to address. Section 7.5 summarizes our main findings and contributions to PAIR, AI, and cognitive science.

7.2 Computational Framework

Bayesian theory of mind (BToM) is a theory-based Bayesian (TBB) framework [126], which models the structured knowledge of human ToM at multiple levels of abstraction, representing the ontology and principles of the theory at an abstract level and mapping these concepts to particular domains and contexts to generate specific predictions and inferences. The TBB approach divides the world into domain-specific theories, with each theory applying its own set of abstract principles to organize the phenomena within its domain. Often these principles consist of sophisticated mechanisms or models, analogous to the principles posited by scientific theories, e.g., a physics engine for intuitive physical reasoning [65], genetic and ecological networks for intuitive biology [120], or rational planning for intuitive psychology [8,130,6]). Theories bridge different levels of abstraction, applying their mechanisms within a specific context (e.g., running a physical simulation that takes the present scene as input) and grounding the output of these mechanisms in the observed data (i.e., establishing the meaning and referents of the theory). TBB analysis has been applied in Cognitive Science [126,59,80] to formulate “rational” [4], “computational-level” [92] or “ideal-observer” [48,81] models of human cognition. This approach can be used to evaluate how closely human judgments approach the ideal Bayesian inferences, but it can also serve to identify which structured representations best explain human judgments under hypothetically unbounded computational resources. Here, we study the representational content of ToM, aiming to show that human inferences closely approach the Bayesian ideal under plausible representational assumptions.

7.2.1 Informal Sketch

BToM represents an observer using a theory of mind to understand the actions of an individual agent within some environmental context. This corresponds to the setting of “keyhole plan recognition” [31] in the PAIR literature. For concreteness, we use as a running example a simple spatial context (e.g., a college campus or urban landscape) defined by buildings and perceptually distinct objects, with agents’ actions corresponding to movement, although in general BToM can be defined over arbitrary state and action spaces (e.g., a card game where the state describes players’ hands and actions include draw or fold). Figure 7.2 shows an example condition from our behavioral experiment. The world is characterized by the campus size, the location and size of buildings, and the location of several different goal objects, here food trucks. The agent is a hungry graduate student leaving his office and walking around campus in search of satisfying lunch food. There are three trucks that visit campus: Korean (K), Lebanese (L) and Mexican (M), but only two parking spots where trucks are allowed to park, indicated in Figure 7.2 by the shaded cells in which K and L are parked. The area of the environment that is not visible from the student’s location is shaded in gray.

Given the information provided by the context, the state space for planning is constructed by enumerating the set of all possible configurations of the dynamic aspects of the world. In our spatial contexts, we decompose the state representation into the world state, which represents the location of all dynamic objects (here, arrangement of trucks in parking spaces), and the agent state, which specifies the objective, physical properties of the agent (e.g., its current location in space, which is assumed to occupy a discrete grid in our experiment). The action space represents the set of actions available to the agent, and the state-transition distribution is constructed to capture the (possibly stochastic) effects of these actions on the world and agent state. In a spatial domain, the actions consist of moving in a particular direction (e.g., North, South, East, West). The state-transition distribution represents the movement that results from attempting these actions from each state, integrating the spatial relations, (e.g., adjacency), and constraints (e.g., walls or obstacles) defined by the environment. Here we assume for simplicity that the world state remains constant across each observed episode.

The observation space represents the set of possible sensory signals an agent can receive, and the observation distribution expresses the observations generated by each state. In a spatial setting, observations depend on the agent’s 360-degree field of view, illustrated by the unshaded regions in Figure 7.2. As an example, in Frames 5 and 15, the agent can observe that K is in the Southwest parking spot but cannot see which truck is in the Northeast parking spot; only in Frame 10 does the observation uniquely identify the world as containing K in the Southwest parking spot and L in the Northeast parking spot. To capture the possibility of failing to see a truck that is actually there, we assume that with a small probability, an agent can mistakenly observe a spot to be empty. This captures the inference, for example, in Figure 7.2 that the agent really did want L but didn’t notice that the truck was in fact parked in the Northeast spot.

The hallmark of ToM is an awareness that others have representational mental states that can differ from our own. The representations we have described so far are assumed to be shared by both the agent and the observer, but the BToM observer also maintains representations of the agent’s representational mental states—beliefs about the agent’s beliefs and desires. The content of the agent’s desire consists of objects or events in the world. The agent’s degree of desire is represented in terms of the subjective reward received for taking actions in certain states (e.g., acting to attain a goal while in close proximity to the goal object). The agent can also act to change its own position (or the state of the world) at a certain cost (e.g., navigating to reach a goal may incur a small cost at each step). Like desires, beliefs are defined by both their content and the strength or degree with which they are held. The content of a belief is a representation corresponding to a possible world. For instance, if the agent is unsure about the location of a particular object, its belief contents are worlds in which the object is in different locations. The agent’s degree of belief reflects the subjective probability it assigns to each possible world.

The principles governing the relation between the world and the agent’s beliefs, desires, and actions can be naturally expressed within partially observable Markov decision processes (POMDPs) [76]. POMDPs capture the causal relationship between beliefs and the world using the principle of rational belief, which formalizes how the agent’s belief is affected by observations in terms of Bayesian belief updating. Given an observation, the agent updates its degree of belief in a particular world based on the likelihood of receiving that observation in that world. POMDPs represent how beliefs and desires cause actions using the principle of rational action, or rational planning. Intuitively, rational POMDP planning provides a predictive model of an agent optimizing the trade-off between exploring the environment to discover the greatest rewards and exploiting known rewards to minimize costs incurred.

On observing an agent’s behavior within an environment, the beliefs and desires that caused the agent to generate this behavior are inferred using Bayesian inference. The observer maintains a hypothesis space of joint beliefs and desires, which represent the agent’s initial beliefs about the world state and the agent’s static desires for different goals. For each hypothesis, the observer evaluates the likelihood of generating the observed behavior given the hypothesized belief and desire. The observer integrates this likelihood with the prior over mental states to infer the agent’s joint belief and desire.

As an example of how this works, consider the scenario shown in Figure 7.2. At first, the agent can only see where K, but not L, is parked. Because he can see K, he knows that the spot behind the building either holds L, M, or is empty. By Frame 10, the agent has passed K, indicating that he either wants L or M (or both) and believes that the desired truck is likely to be behind the building—or else he would have gone straight to K under the principle of rational action. After Frame 10, the agent discovers that L is behind the building and turns back to K. Obviously, the agent desires K more than L, but more subtly, it also seems likely that he wants M more than either K or L; this attribution is made without explicit observation of the choice for M–even without M being present in the scene. BToM captures this inference by resolving the desire for L or M over K in favor of M after the agent rejects L. In other words, BToM infers the best explanation for the observed behavior—the only consistent desire that could lead the agent to act the way he did.

7.2.2 Formal Modeling

This section provides mathematical details of the BToM framework sketched previously; this can be skipped by the casual reader. First, we describe the construction of the state space, action space, state-transition distribution, observation space, and observation distribution used for POMDP planning. We then derive the formation and dynamics of the BToM representation of agents’ beliefs and desires. Finally, we derive the Bayesian computations that support joint belief and desire inference, then explain how model predictions are generated for our experiment.

In the food-truck domain, the agent occupies a discrete state space image of points in a 2D grid. The world state space image is the set of possible assignments of the K, L, and M trucks to parking spots (consisting of 13 configurations in total). For simplicity, we assume that the world is static (i.e., that the locations of the trucks do not change over the course of a episode), although the extension to dynamic worlds is straigntforward (e.g., allowing trucks to arrive, depart, or move). The action space image includes actions North, South, East, West, Stay, and Eat. The state-transition distribution image represents the conditional probability of transitioning to agent state image at time image, given the world image, the agent state image, and action image at time image. Valid movement actions are assumed to yield their intended transition with probability image and to do nothing otherwise; invalid actions (e.g., moving into walls) have no effect on the state. The Eat action is assumed to lead to a special “Finished” state if selected when the agent is at the location of a food truck and to have no effect on the state otherwise.

The agent’s visual observations are represented by the isovist from its present location: a polygonal region containing all points of the environment within a 360-degree field of view [36,94]. Example isovists from different locations in one environment are shown in Figure 7.2. The observation distribution image is constructed by first computing the isovist for every agent and world state pair in image. Then, for each agent state image, the isovists for all worlds image are compared to establish which sets of worlds are perceptually distinguishable from that agent state. In the food-truck domain, worlds are distinguished by the locations of the food trucks.

We assume that the probability of observing which truck is in a parking spot is proportional to the area of that grid cell contained within the isovist. We model observation noise with the simple assumption that with probability image, the agent can fail to notice a truck’s presence in a parking spot, mistakenly observing the symbol that “nothing” is there instead. From a given agent state, all perceptually distinguishable worlds are assumed to generate different observation symbols; worlds that are indistinguishable will emit the same observation symbol. For example, in Figure 7.2, Frames 5 and 15, the observation symbol will be consistent with only worlds containing the Korean truck in the Southwest parking spot and either the Lebanese truck, Mexican truck, or nothing in the Northeast parking spot. The observation symbol in Frame 10 will uniquely identify the state of the world.

Students are assumed to know their own location image (and the location of all buildings and parking spots) but can be uncertain about the state of the world image (i.e., the truck locations); technically, this induces a particular kind of POMDP called a mixed-observability MDP [98]. The observer represents the agent’s belief as a probability distribution over image; for image denotes the agent’s degree of belief that image is the true world state. In the food-truck domain, image represents students’ beliefs about which trucks are where. As agents receive observations, they are assumed to perform Bayesian belief updating to integrate image, the probability their belief assigns to world image at time image with two likelihood functions2: image, the probability of making the observed transition from image to image given action image in world image; and image, the likelihood of generating observation image, given the agent state image and world image:

image(7.1)

From the agent’s perspective, given image and image, the belief update at time image is a deterministic function of the prior belief image, the action image, and the previous agent state image. As a shorthand for this deterministic computation, we write:

image(7.2)

BToM assumes that agents’ desires are defined over classes of states, actions and “events” (state transitions), and that each desire has an associated “degree” or strength. In the food-truck domain, agents’ desires correspond to eating at one of several food trucks, but their degree of desire for each truck is unknown. Within the POMDP model, eating events are represented as state transitions from a truck location to the “Finished” state. The degree of desire for each truck is embedded within the agent’s reward function image, where image is the location of a truck in world image, and image. This reward represents the subjective utility the agent receives for eating at the truck located at image. The reward function also represents the costs (negative rewards) the agent incurs for movement actions, which are each assumed to have a cost of 1. Once the student has eaten (i.e., transitioned to the absorbing “Finished” state), all rewards and costs cease, implying that rational agents should optimize the trade-off between the distance traveled versus the reward obtained, choosing which truck to visit based on its desirability, the probability that it will be present, and the total cost to reach its location.

The representations defined so far provide the input to the POMDP planning mechanism of BToM. The output of the POMDP solver is the value function image, where image is the agent’s image-dimensional belief vector and image is an agent state. Given image, the agent’spolicy is computed, which represents the probability distribution over the agent’s actions, given its beliefs and location. 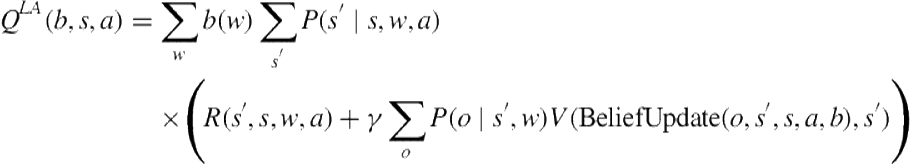First, the lookahead state–action value function [70] image is computed to integrate the expected immediate cost of action image with the expected discounted future value of taking that action:

image(7.3)

The agent’s policy image is assumed to stochastically maximize the lookahead state–action value function using the softmax function:

image(7.4)

The image parameter establishes the degree of determinism with which the agent executes its policy, capturing the intuition that agents tend to, but do not always, follow the optimal policy.

A wealth of algorithms and off-the-shelf solvers are applicable to the (relatively simple) POMDPs of our food-truck domain. Because many of the probabilistic computations involved in solving these POMDPs are shared with the inferential component of BToM, we implement one of the simplest approximate POMDP solvers, based on discretizing the real-valued belief space with a set of belief points drawn from a regular grid, and applying the value iteration algorithm to these points [88]. The value of arbitrary beliefs is then obtained by linearly interpolating between the values at the neighboring grid points; this provides a piecewise-linear upper bound to the optimal value function.

Together, the state-transition distribution and the agent’s policy, belief updating function, and observation distribution comprise the BToM observer’s predictive model of the agent’s behavior and mental states. These representations are composed to form the structured probabilistic model in Figure 7.3, which takes the form of a dynamic Bayesian network (DBN) described by Murphy [95]. The most basic computation the DBN model supports is forward-sampling: given initial belief image, desire image, world state image, and agent state image, drawing samples from the joint distribution over all variables in the network involves sequentially sampling from the conditional distributions in Figure 7.3. 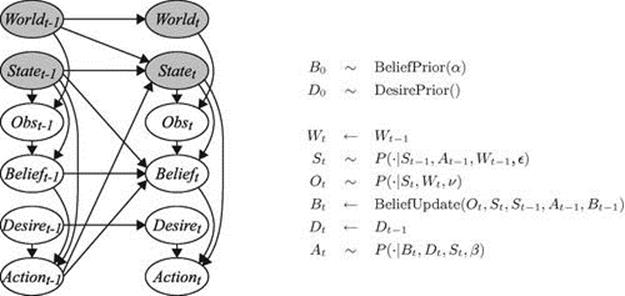This is the process by which the BToM observer assumes an agent’s trajectory to have been generated, only with initial beliefs image and desires image that are unknown to the observer and must be inferred.

image

FIGURE 7.3 Observer’s grounding of the theory as a dynamic Bayes net.Variables in the DBN are abbreviated by their first letter, the “image” symbol denotes “is distributed as,” and the “image” symbol denotes deterministic assignment. The DBN encodes the observer’s joint distribution over an agent’s beliefs image and desires image over time, given the agent’s physical state sequence image in world image. For simplicity, we assume that the world image and the agent’s desire image remain constant over the course of an episode.

Bayesian inference of an agent’s beliefs image and desires image, given its observed trajectory image in world image, requires prior probability distributions over the agent’s initial beliefs and desires to be specified. To tractably represent these priors over the multidimensional, continuous space of beliefs, we discretize the belief simplex image using the Freudenthal triangulation [88] of resolution image to generate image initial belief points image. Each initial belief point image is assigned prior probability proportional to the density ofimage at image, assumed to be a image-dimensional symmetric Dirichlet distribution with parameter image. Similarly, in our scenarios, the agent’s actions depend on its desires for the three different food trucks, and we generate a regular 3D grid with resolutionimage to represent image hypotheses image about the agent’s joint desires for each truck. For simplicity, we assume a uniform prior over the space of desires, denoted DesirePrior ().

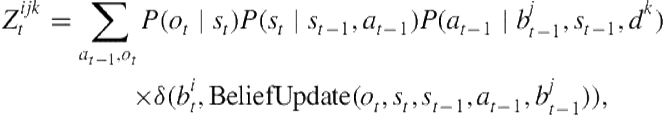Given the agent’s state sequence image in world image, reasoning about the agent’s beliefs and desires over time is performed using the belief-propagation algorithm, a standard approach to inference in DBNs. For clarity, we describe belief–desire inference in BToM by analogy to the forward–backward algorithm for inference in hidden Markov models (HMMs) [105], a well-known special case of belief propagation. At each timestep, given the set of belief points image at the previous timestep, a new set of image belief points, image is generated by applying the BeliefUpdate () function to each pair of possible actions and observations image of the agent. To determine the probability of transitioning from each image to each image (given desire hypothesis image), we compute a belief- and desire-transition matrix image, summing over all actions image and observations image that could yield the transition:

image(7.5)

where the image-function equals 1 when image and 0 otherwise. This ensures that only prior beliefs image, observations image, and actions image that produce the belief update image enter into the summation.

As in HMMs, an online estimate of the state of the system—in this case, the beliefs and desires that constitute the agent’s mental state—is given by the forward distribution:

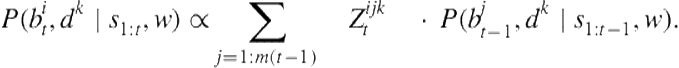image(7.6)

This provides the marginal posterior distribution over the agent’s beliefs and desires, given all the information provided by the agent’s trajectory up to time image. The recursive matrix multiplication in Eq. 7.6 resembles the filtering computation within HMMs, but with a nonstationary, context-dependent transition matrix defined over two jointly distributed variables. It is also related to the algorithm for filtering over infinitely nested beliefs proposed by Zettlemoyer et al. [146]; here, we consider a special case with only one agent, but extend their algorithm to jointly infer desires in addition to beliefs.

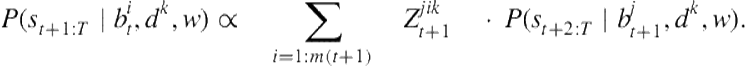Next, we define the backward distribution, which recursively propagates information backward in time to give the marginal likelihood of the agent’s future trajectory up to time image, given its mental state at some past time point image:

image(7.7)

Together, the forward and backward distributions allow us to compute the joint posterior marginal over the agent’s beliefs and desires at time image, given the state sequence up until image. This is given by the product of the forward and backward distributions, called the smoothing distribution:

image(7.8)

This computation is analogous to the forward–backward algorithm in HMMs. Equation 7.8 provides the basis for model predictions of people’s joint desire and retrospective belief inferences in our experiment.

7.2.3 Alternative Models

To test whether the full representational capacity of BToM is necessary to understand people’s mental state attributions, we formulate two alternative models as special cases of our joint inference model. Each alternative model “lesions” a central component of the full model’s representation of beliefs, and tests whether it is possible to explain people’s inferences about agents’ desires in our experiment without appeal to a full-fledged ToM.

Our first alternative model is called TrueBelief. This model assumes that the true world state is fully observable to the agent, implying that the agent has true beliefs about the location of every truck and plans to go directly to the truck that will provide the maximum reward while incurring the least cost. Technically, TrueBelief uses an MDP generative model of the agent’s behavior, instead of the more complex, more computationally intensive POMDP model used by BToM. We formulate the TrueBelief model by modifying the agent’s beliefs (i.e., the BeliefPrior () distribution and BeliefUpdate () function) to assign probability 1 to the true world state image:

image(7.9)

We hypothesized that TrueBelief would correlate moderately well with people’s desire judgments because of the statistical association between desired objects and actions. In addition, if people’s belief attributions are highly influenced by the true state of the world in each condition, their belief judgments should correlate strongly with the TrueBelief model predictions.

Our second alternative model is called NoObs. In this model, the agent’s initial belief about the world state is generated from the image distribution in the same manner as in BToM (see Figure 7.3), but the BeliefUpdate () function is modified so that the initially sampled belief remains fixed throughout the trial (as if the agent was “blindfolded,” or otherwise unable to observe the world state):

image(7.10)

We hypothesized that this model might fit people’s belief and desire inferences in situations where the agent appears to move toward the same truck throughout the entire trial, but that for actions that require belief updating or exploration to explain, for instance, when the agent begins by exploring the world, then changes direction based on observation of the world state (e.g., Figure 7.2), NoObs would be a poor fit.

7.2.4 AI and ToM

The long association between psychology and PAIR research in AI provides important touchstones for our work. From the perspective of this chapter, the key threads running through research on understanding agents and actions in philosophy, psychology, linguistics, and AI are:

1. Modeling others as intentional agents with representational mental states such as beliefs and desires

2. Framing PAIR as a problem of probabilistic inference over generative models of behavior.

Both of these assumptions are fundamental to our work here.

An explicit connection with “commonsense psychology” was made by the earliest literature on plan recognition [111,113,139], which arose from multiple fertile collaborations between AI and social psychology researchers. Plan recognition also became an important component within models of pragmatics and discourse understanding in linguistics [102,3,60,86,32]. Inspired by speech-act theory [5,116] and Gricean pragmatics [58], these approaches assume that speakers have a representation of listeners’ knowledge, beliefs, desires, and intentions (expressed in modal or first-order logic), and use these representations to plan utterances to influence interlocutors’ mental states and behavior [33].3

Classical accounts of plan recognition were motivated conceptually in terms of reasoning about intentional action—the first key thread identified above—but in practice inference in these models typically involved heuristic, rule-based reasoning about the speaker’s beliefs, desires, intentions, and planning process [111,102,3]. Although general algorithmic approaches to inference about classical planning agents were later developed by Kautz and Allen [79,78], logical approaches to plan recognition remained limited by the difficulty of capturing naturalistic behaviors in purely logical terms, and by the inability of logical inferences to capture the gradedness and ambiguity inherent in human mental state attributions.

A subsequent generation of models picked up the second key thread, formulating PAIR as a problem of probabilistic inference over context-dependent, generative models of actions [27,2,53,104,20,47]. However, unlike the previous generation of plan-recognition approaches, these models do not explicitly employ planning algorithms to generate models of agents’ actions. Instead, they either assume that probability distributions over intention- or goal-dependent actions are specified a priori [27,53,104,20,47], or that they are learned from a corpus of previously observed behavior [2]. Given observed actions, the plan, goal, or intention most likely to have generated them can be inferred using Bayes’ rule.

Recent approaches have also applied discriminative probabilistic models to PAIR [85,131], directly learning the structure and parameters of the conditional distribution over activities and goals, given behavioral observations. These probabilistic PAIR techniques perform graded inferences, and given sufficient data, they can learn the appropriate probability distributions over real-world behavior. They can also achieve generalization to new contexts and activities using abstract, structured representations of environments, actions, and goals. However, without explicit representations of intent- or goal-directed planning—the purposeful, adaptive processes captured by classic accounts of PAIR—these models’ generalization beyond the realm of previous experience is fundamentally limited.

Recent work across a number of fields has begun to tie together the two key threads running through previous PAIR research. Within the field of economics, the seminal “Bayesian games” framework of Harsanyi [67–69] and research in behavioral economics and behavioral game theory [122,72,21,22] have modeled the degree to which people represent and reason about other players’ types, encompassing information about their utility functions, knowledge, and strategic reasoning processes. Research in the fields of multiagent systems and human–computer interaction has also explored these issues [52,93,44,51,45,40], modeling agents’ recursive reasoning about each others’ utility functions, strategies, and plans and recently framing these representations in terms of ToM [103,121,39]. Although these approaches focus on the need for recursive representations of intentional agents in interactive contexts (rather than on PAIR per se), the probabilistic inferences over models of intentional agents’ planning they perform integrate the key threads of both classic and probabilistic PAIR models.

Within the field of machine learning, Ng and Russell [97] formulated the problem of inferring an agent’s utility function to explain its behavior in terms of “inverse reinforcement learning” (IRL; also see Chajewska and Koller [25]). Reinforcement learning describes the problem facing an agent figuring out how to act to maximize reward in an unknown environment [124]. Inverse reinforcement learning is the opposite problem: given data on how an agent behaves, determine the unknown reward function it is maximizing. In recent years, IRL (also known as “inverse optimal control”) has seen increasing interest in Machine Learning, yielding an expanding number of theoretical and applied results [26,1,106,96,41,147,135,28].

In the field of cognitive science, a rapidly growing body of research, complementing game–theoretic and IRL-based approaches to PAIR, has suggested that human judgments about intentional agents’ mental states (i.e., goals, intentions, preferences, desires) can be modeled as probabilistic inverse planning, or inverse decision making–Bayesian inferences over predictive models of rational, intentional behavior [9,133,54,10,7,143,8,55,89,130,16,144,125,74,75,73,123]. Closely related to, but preceding these approaches, models of motor control have been applied to capture the understanding and imitation of physical movement [141,100,109]. Recent research has also begun to develop probabilistic versions of the ideas from pragmatics and discourse understanding previously discussed in similar terms [43,56], and similar models of intentional communication have been effective in modeling pedagogy as well [119].4

An array of alternative approaches to modeling ToM have been proposed in cognitive science as well. Logical frameworks analogous to classical PAIR models have been formulated in terms of rule-based schemas [112,115,134], and more recently expressed in the cognitive architecture Polyscheme [23] to capture the dynamics of cognitive processing during ToM reasoning [14,15,13,12]. Accounts analogous to discriminative probabilistic models have been expressed both as connectionist models [132,17], and in terms of low-level motion cue-based action categorization [18,11,145]. Elsewhere, we have compared the ability of heuristic or cue-based versus inverse-planning accounts to quantitatively fit human judgments [7,8,130,73], arguing that models of planning, rather than simple heuristics or low-level cues, are core mental representations of ToM.

7.3 Comparing the Model to Human Judgments

Given the diverse range of AI and cognitive models relating to human ToM, how can we evaluate these models, both in terms of their quantitative fit to human behavior, and in terms of their real-world practicality and performance? Here we describe a range of scenarios, set within our food-truck domain, that can be presented to both human subjects and computational models. These scenarios systematically vary the observed actions, the environmental constraints, the truck locations, and the costs incurred for executing a particular trajectory. This establishes a natural setting for ToM reasoning, involving agents with varying beliefs and desires, whose actions depend on these factors as well as the structure of environment.

As illustrated earlier in Figure 7.2, these food-truck scenarios can be presented to human subjects as animated 2D displays of agents navigating through simple “grid-world” contexts. In Figure 7.2, the agent and trucks’ locations are marked by small sprites, buildings are marked by black grid squares, and potential parking spaces are marked by shaded grid squares. These details determine the agent’s line-of-sight visibility, which is illustrated by the unshaded region of space surrounding the agent. Similar 2D animations have been shown to evoke strong impressions of agency and intentionality in infant [50,64] and adult [71,128,129] observers, and have been employed in several computational studies of human-action understanding [8] and social goal inference [18,130]. They are also known to recruit brain regions that have been implicated in the perception of animacy and biological motion [114,24,83,46].

People’s intuitive judgments on viewing these animated stimuli can be elicited behaviorally using psychophysical methods. In the food-truck context, people can report their desire attributions by rating how much the student liked each truck, and their belief attributions by retrospectively rating the student’s degree of belief in each possible world—Lebanese truck (L), Mexican truck (M), or nothing (N) parked in the Northeast spot—before they set off along their path, based on the information from their subsequently observed trajectory. Both kinds of ratings can be expressed using a 7-point Likert scales.

Applying BToM to our food-truck scenarios requires specifying a number of settings and parameters. We select resolutions image for discretizing the belief and desire spaces, respectively. This directly corresponds to the 7-point psychological scale for human ratings, providing sufficient resolution to represent the joint probabilistic dependencies between beliefs and desires and allowing inference to be performed relatively tractably. The range of reward values is calibrated to the spatial scale of our environments, taking values −20, 0, …, 100 to represent desires ranging from aversion, to ambivalence, to a strong desire for each truck. These desires trade off against the relative cost of movements, assumed to be equal to 1 for each step, with 15 steps required to cross the environment from East–West and 5 steps required to cross from South–North.

Model predictions are based on the student’s expected reward value for each truck (K, L, M) and the expected degree of belief in each possible world (L, M, N) for each trial, where the expectation is taken over the posterior marginal distribution in Eq. 7.8. Two free parameters are fit for the BToM model: image, which specifies the agent’s degree of determinism in selecting the best action, and image, which specifies the agent’s level of observation noise. Only the determinism parameter image is relevant for the TrueBelief and NoObsmodels and is set for them as well. Parameter fits are not meant to be precise; we report the best values found among several drawn from a coarse grid. The remaining parameters, image, the Dirichlet hyperparameter for the image distribution, and image, the movement noise in the state-transition distribution, are set to default values: image to produce a uniform prior over beliefs, and image to reflect a very small probability of the agent’s intended movements failing.

Next, we provide a detailed demonstration of some of the rich dynamical inferences made by BToM, using the food-truck scenario shown in Figure 7.2. Initially, the agent can see that the Korean (K) truck is in the Southwest parking spot, but the Northeast parking spot is not visible from its location—it may believe that either the Lebanese (L) truck, the Mexican (M) truck, or Nothing (N) is parked there, or be uncertain which of these possibilities is the case. At first, the agent heads in the direction of the Korean truck, which is also the shortest route to reach the Northeast parking spot or to see what is there. The agent then passes the Korean truck, rounds the corner to see the Northeast parking spot, sees that the Lebanese truck is parked there, and turns back to eat at the Korean truck.

Over the course of this simple scenario, BToM performs a range of nuanced, but intuitive, types of temporal inferences, all of which can be expressed as different queries over Eq. 7.8. Figure 7.4 plots examples of several of these types of mental state reasoning over time. The most straightforward inferences are those about an agent’s current mental state, given its actions up to the present time, referred to as online inferences. For example, the annotated stimulus in Figure 7.4(a) illustrates online inference of the agent’s mental state at time 10, given its movements up to that point. More conceptually challenging are retrospective inferences, shown in Figure 7.4(b), which are about the agent’s beliefs at some past moment, given its trajectory prior and subsequent to that moment. The annotated stimulus in Figure 7.4(b) depicts retrospective inference of the agent’s initial mental state at time 1, given its full trajectory up to Step 15, once it has arrived at K.

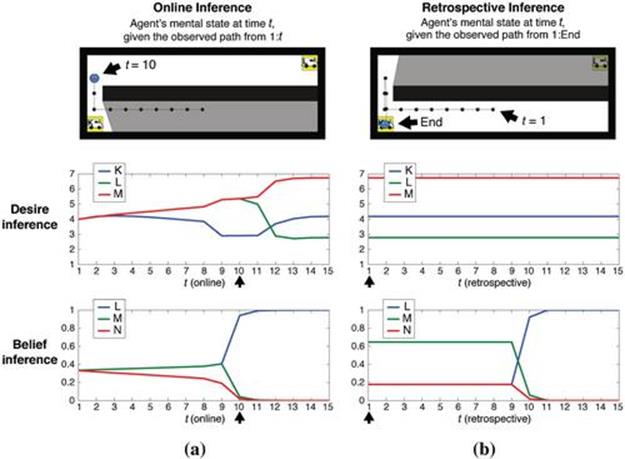
image

FIGURE 7.4 Online and retrospective desire and belief inferences in BToM.In each stimulus panel, the marked path up to the position of the agent indicates the portion of the trajectory observed: in (a), up to image; in (b), up to image. The arrow in each stimulus panel indicates the point in time at which the agent’s mental state is queried: in (a) at image; in (b) at image. For each plot of the model inferences, the arrows along the X axis indicate the timestep shown in the annotated example stimulus. (a) Online inference of the agent’s desires and beliefs, given its partial trajectory. (b) Retrospective inference of the agent’s desires and beliefs at each frame, given its entire trajectory.

BToM’s online desire and belief inferences plotted in Figure 7.4(a) correspond closely to the intuitive mentalistic description of the scenario given in Section 7.2.1. The model initially infers that the agent desires K, L, and M equally, and believes that L, M, or N are equally likely to be in the Northeast parking spot. Gradually, BToM infers that the agent desires L and M over K and desires L and M equally. The model also gradually infers that the agent believes that either L or M is more likely to be in the Northeast parking spot than N. By Frame 10, the inferred desire for L or M over K has strengthened after the agent passes K. Once the agent gains line-of-sight visual access to the Northeast parking spot, the model strongly infers that the agent’s belief resolves toward L—the true state of the world. At Frame 11, the agent pauses in the same position for one timestep, which causes the model’s desire attributions for M and L to begin to diverge; by Frame 12, the agent’s full desire ordering has been inferred: M is desired over K and both M and K are desired over L.

These online inferences are intuitive and demonstrate the potential for ToM reasoning to go beyond the data given, but the retrospective inferences made by BToM go further still. BToM retrospectively explains the agent’s entire trajectory by inferring the agent’s full sequence of mental states—its desires and beliefs at each point in time, how they caused its actions, and how they were affected by its observations. Earlier in Figure 7.4(b), BToM retrospectively attributes that the agent had a strong false belief before Frame 10 that M was in the Northeast parking spot. Contrast this with the online inference, shown in Figure 7.4(a), which infers the agent’s belief at each frame based only on the information available up to that point, and thus cannot distinguish whether the agent believes L or M to be more likely. After frame 10, the online and retrospective inferences match—because the agent has observed the Northeast parking spot, both models attribute the true belief that L is there, and no further changes occur. BToM retrospectively attributes an intense desire for M, a weak desire for K, and almost no desire for L. Note that the retrospective desire inference matches the online inference in Figure 7.4(a) at the last timestep because both reflect the agent’s entire movement history, and the inferred desire is assumed to be constant over the agent’s trajectory.

So far we have shown that BToM makes rich, intuitive predictions about the patterns of mental state inferences induced by our food-truck scenarios. Now we test how accurately these predictions, as well as those of our alternative models, fit human behavioral judgments. Figure 7.5 presents revealing comparisons of human judgments with model predictions in several specific cases. Example A compares behavioral and modeling results for our running example scenario introduced in Figure 7.2, and analyzed with BToM in Figure 7.4. For both desire and belief inferences, people’s judgments in Condition A closely match the predictions of BToM but not those of the two alternative models. In this condition, both humans and BToM infer that the agent desires M most, K second most, and L least, while NoObs and TrueBelief incorrectly infer that K is most strongly desired because, superficially, it is the agent’s eventual destination. Humans and BToM attribute the false belief to the agent that M is most likely to be in the Northeast parking spot, which (necessarily) differs from the TrueBelief inference, but also that of NoObs, which makes no specific prediction in this case.

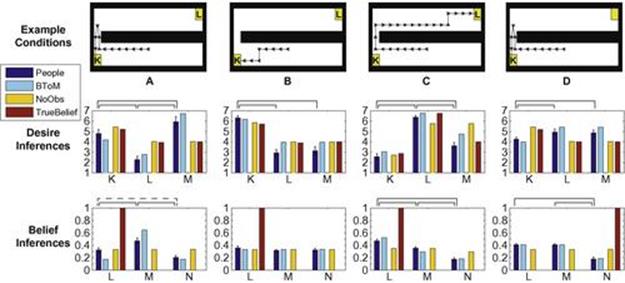
image

FIGURE 7.5 Four representative conditions from the experiment, illustrating experimental stimuli, and corresponding mean human desire and belief judgments alongside BToM, NoObs, and TrueBelief model predictions.Desire attributions were performed for trucks K, L, or M, rated on a scale of 1 to 7, and belief attributions were made about the agents’ initial beliefs about the contents of the Northeast parking spot—either truck L or M or no truck (N)—rated on a 1 to 7 scale, and normalized to a probability scale from 0 to 1. Error bars show standard error (nimage16). Solid brackets indicate differences between pairs of human ratings that were predicted by the model. The bracket in example Condition A between L and N indicates the sole difference that the model did not predict.

Further examples of the close correspondence between human judgments and BToM predictions are shown in Conditions B, C, and D of Figure 7.5. The simplest example is Condition B in which the agent moves directly to K without first checking the contents of the Northeast parking spot. People and all models correctly attribute a strong desire for K, and infer that L and M are probably desired equally. BToM and NoObs match people’s judgment that the agent’s belief is ambiguous between all possible worlds because the strong desire inferred for K renders this belief irrelevant to the agent’s behavior.

In Condition C, the agent’s path initially overlaps with that of Condition A, but once the Northeast parking spot is in view, the agent continues onward to reach the L truck. Here, humans, BToM, and TrueBelief infer that L is desired most, M second most, and K least. BToM also predicts people’s belief attributions, with L being most likely, M second most likely, and N least likely. However, NoObs does not distinguish between L or M for either desires or beliefs. The explanation for the maximal desire and belief ratings for L is straightforward, but the systematically elevated desire and belief ratings for M are more subtle and interesting. For these ratings, BToM infers that the agent may have desired both L and M over K, and initially believed M to be in the Northeast parking spot. Indeed, this hypothesis could also explain the observed trajectory, but the evidence for it is weak and indirect, which is reflected in the relatively weaker ratings for M than L.

Condition D is similar to Condition A but with an empty Northeast parking spot. As in Condition A, only BToM predicts the pattern of people’s inferences for desires and beliefs. Here, it is ambiguous whether the agent most desires L or M, or which one it believes to be present, and people’s judgments reflect this, with their desire ratings for L and M greater than for K, and their belief ratings for L and M greater than for N. In this case, NoObs and TrueBelief make desire attributions that are identical to those made in Condition A because both are unable to reason about the role of the agent’s beliefs and observations in determining its behavior.

Finally, we analyze the overall quantitative fit between people’s judgments and our three models. Over 54 conditions in total, BToM predicted people’s judgments about agents’ desires closely (image), and less well, but still reasonably for judgments about agents’ initial beliefs (image). NoObs and TrueBelief fit substantially worse than BToM for desire judgments (image and image, respectively), suggesting that joint reasoning over desires and beliefs is essential for explaining people’s desire attributions. The NoObs model can in principle infer agents’ beliefs but without a theory of how beliefs are updated from observations, it must posit highly implausible initial beliefs that correlate poorly with subjects’ judgments over the whole set of experimental conditions (image). TrueBelief’s belief predictions are based on the actual state of the world in each trial; the poor correlation with people’s judgments image demonstrates that they did not simply refer to the true world state in their belief attributions.

7.4 Discussion

This chapter described a model of human theory of mind inspired by techniques in plan, activity, and intent recognition and artificial intelligence. We argued that the central representations of ToM can be understood as intuitive versions of the formal models of intelligent agents developed by AI researchers and economists, supporting rich, context-sensitive simulations of the thoughts and plans of others. Our Bayesian ToM model formulated reasoning about others’ mental states as probabilistic inference over these intuitive models, yielding rich attributions of beliefs and desires from sparsely observed behavior. To test these models, we proposed an approach to rigorously evaluating computational models of ToM against fine-grained human judgments, which showed a strong quantitative correspondence between BToM and human inferences.

Although this chapter has focused on reasoning about the activities of individual agents within simple spatial situations, in related work we have extended our models to multiagent situations involving competitive or cooperative interactions, e.g., chasing and fleeing [7] or helping and hindering [130,62]. In these domains, our generative models of agents’ interactive behavior take the form of Markov games [87] (see Gmytrasiewicz and Doshi [51] and Doshi et al. [39] (this book) for related multiagent planning formalisms). Inference is performed over agents’ social goals, beliefs, and other mental states using Bayesian computations similar to those described in this chapter. For example, Figure 7.6 compares human inferences with theory- and heuristic-based model inferences of whether each of two agents is “chasing” or “fleeing” the other across three simple environmental contexts. At a coarse level, people’s judgments are sensitive to the agents’ relative movements (i.e., “toward” or “away” from the other agent), which both the theory- and heuristic-based models capture, but they also exhibit fine-grained variation as a function of the environment, which only the theory-based model is able to explain by reasoning about the agents’ context- and goal-dependent planning.

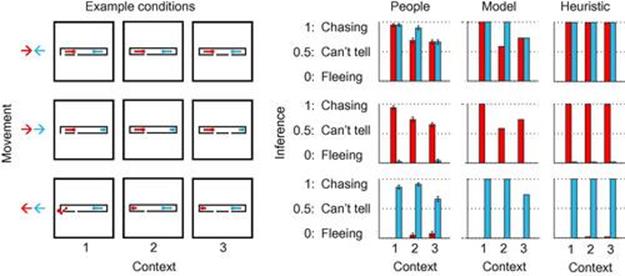
image

FIGURE 7.6 Example stimuli and results from an experiment on inferring “chasing” or “fleeing.”Stimuli consist of a dark agent and light agent occupying a discrete grid world, with obstacles and boundaries marked by black grid squares. The different agents occupy opposite sides of a long enclosing “room,” with their location indicated by large dots, and their path history illustrated by the dotted trail extending behind them. A image subset of the experimental design is shown, with three different environmental contexts and three different relative movement patterns. The three contexts differ in the exits available at each side of the room, and the three relative movement patterns are “dark moves toward light and light moves toward dark,” “dark moves toward light and light moves away from dark,” and “dark moves away from light and light moves toward dark.” Experimental subjects inferred whether each agent was “chasing” or “fleeing” the other. Two models were compared with human judgments: a theory-based model, which assumed that agents use representations of each others’ goals to plan actions to achieve their own goals, and a heuristic-based model, which used minimizing or maximizing geodesic distance as correlates of chasing and fleeing, respectively. Both models capture the coarse structure of people’s judgments, which reflects the agents’ relative movements, but only the theory-based model captures the fine-grained, joint dependence of people’s inferences on both the agents’ movements and the environmental context.

Generally speaking, AI models of (approximately) rational planning, including MDPs, POMDPs, and multiagent extensions such as Markov games [87], interactive POMDPs [51], and partially observable stochastic games [66] are becoming increasingly practical for real-world applications. As algorithms for solving these problems improve, so will the ability of our computational models to perform forward-simulation of agents’ mental state-dependent behaviors in realistic contexts. As described here, the inverse inference problems involved in ToM are strictly more difficult than the forward-planning problems; however, tractable optimization- and search-based algorithms for solving the inverse problems have been the focus of promising ongoing research [97,1,96,147,41,28]. Thus, although the BToM framework can surely be generalized outside of the spatial situations presented in this chapter, its capacity to quantitatively predict human reasoning beyond our examples remains an open question for future research.

Another open question concerns whether alternative models can explain human ToM judgments with accuracy and precision comparable to BToM. Here, we tested two simplified alternatives to BToM, and other work [8,130,73,101] has considered several models based on discriminative or generative statistical inference (prominent theoretical alternatives discussed in Section 7.2.4 [18,145,2]). In the settings we have tested, variants of BToM uniformly outperform these alternative models, but it is possible that PAIR is supported by different mechanisms in other settings, in particular, those in which strict notions of rationality are ill-defined [101].

From a practical standpoint, the suitability of BToM for engineering PAIR systems depends on two factors: whether AI models of intentional agents are actually the correct generative models of naturalistic behavior within a given setting and whether the Bayesian computations BToM requires can be tractably approximated. In domains similar to the present experimental setting, it is plausible that these conditions are satisfied. Foraging and spatial navigation, as instantiated within our food-truck scenario, are very natural tasks even for infants; they are evolutionarily ancient and necessary for the survival of our species [34,19,11,82], and we can gain volumes of experience performing and observing others perform them throughout the lifespan. Therefore, it is plausible that humans behave near rationally, have finely tuned expectations that others will behave near rationally, and perform reasoning in ways that come impressively close to the optimal Bayesian inferences within these domains.

Of course, none would argue that human behavior is strictly rational under all circumstances [77]–is BToM simply inapplicable to these situations? In fact, Saxe’s “argument from error” cites a body of research showing a systematic dissociation between people’s expectations that others will behave rationally, and the behavior that others actually produce, as evidence for a rationality-based ToM [110]. Although overattribution of rationality constitutes a departure from ideal observer or rational inference in the sense defined earlier, an advantage of predictive models of rational planning is their ability to generalize to novel contexts, allowing behavior to be understood far outside of the familiar situations encountered in everyday life. Furthermore, the rationality assumption may provide a general space of prior models that is refined as more data from others’ or even one’s own behavior are observed. Additional data could even be “simulated” offline using neural mechanisms for decision making; these possibilities highlight the prospect of a hybrid account combining the strengths of planning- and statistically-based mechanisms within the BToM framework. Elucidating the role of these and other mechanisms within a range of contexts by comparing actual behavior, predicted behavior, and interpreted behavior is a promising next step within the BToM research program defined in this chapter.

Under circumstances where BToM and human inferences diverge, this may be because people’s expectations are sensitive to others’ systematic deviations from strict rationality in ways that our present models do not capture. Developing formal models of the complex psychological factors influencing real-world decision making is the goal of the burgeoning fields of behavioral economics [21] and neuroeconomics [37]; as research in these fields produces more realistic models of human behavior, integrating these models within theory-based Bayesian models of ToM will be a promising avenue for improving PAIR systems, perhaps bringing them more in line with human intuitions as well. In other cases, discrepancies between BToM and people could result from fundamental human processing constraints, in the spirit of Chomsky’s “competence-versus-performance” distinction [29]. Understanding people’s approximate inference strategies at the algorithmic [92] or process [4] levels is essential for identifying these cases and could suggest adaptive, resource-constrained algorithms for AI systems to emulate. On the other hand, these areas provide opportunities where computational social intelligence may eventually surpass and augment human intelligence.

Our experimental finding that people’s inferences about agents’ desires are more robust than their inferences about beliefs, and more consistent with our Bayesian model’s predictions, is intriguingly consistent with classic asymmetries between these two kinds of mental state attributions in the ToM literature. Intentional actions are the joint consequence of an agent’s beliefs and desires, but inferences from actions back to beliefs are frequently more difficult and indirect than inferences about desires. Actions often point with salient perceptual cues directly toward an agent’s goal or desired state. When a person wants to take a drink, her hand moves clearly toward the full glass of water on the table. In contrast, no motion so directly indicates what she believes to be inside the glass. Infants as young as five months old can infer agents’ goals from their actions [49], while inferences about representational beliefs seem to be present only in rudimentary forms by one year of age [99] and in more robust forms only by age four [137]. Whether these differences are best explained at the competence level, in terms of modifications to the theory of belief-dependent planning described here or at the performance level, in terms of fundamental cognitive processing constraints, is a crucial question for future study.

7.5 Conclusion

Research on plan recognition began with the idea that AI models of planning can be used in reverse to understand as well as generate behavior. This chapter identified a strong connection between this classic AI idea and human social intelligence, modeling human ToM within a theory-based Bayesian framework inspired by work in AI, PAIR, and machine learning. It is fascinating to find such close parallels between AI and human cognition, but perhaps it should not be too surprising. AI modeling has always been informed by introspection on human intelligence, and cognitive science has always looked to AI for representations and algorithms to explain the abstract computations performed in the human mind and brain. It makes good sense that formal theories of planning should mirror our intuitive theories of what it means to be an intelligent agent because their design has been guided by ToM in the minds of AI researchers.

In the real world, humans still far surpass even the most advanced artificial social intelligence. We believe that engineering PAIR systems with humanlike ToM, using the same kinds of probabilistic models and action representations that support social reasoning in humans, will help to narrow this gap, while also advancing our basic scientific understanding of human social cognition. While psychologists have long studied ToM and action understanding using behavioral experiments, they did not have rigorous computational models of these capacities, framed in the same terms used to engineer AI systems. That is changing as modern PAIR research (and AI more broadly) offers tools to recast the relevant areas of psychological and behavioral science as engineering (or more accurately, “reverse engineering”) disciplines. Engineering large-scale PAIR systems that integrate models of ToM will provide the most challenging test yet of these models’ adequacy and, if successful, demonstrate the need for continual exchange of ideas and techniques between AI and cognitive science.

References

1. Abbeel P, Ng AY. Apprenticeship learning via inverse reinforcement learning. Proceedings of the 21st International Conference on Machine Learning. 2004.

2. Albrecht DW, Zukerman I, Nicholson AE. Bayesian models for keyhole plan recognition in an adventure game. User Model User-Adapt Interact. 1998;8(1–2):5-47.

3. Allen JF, Perrault CR. Analyzing intention in utterances. Artif Intell. 1980;15:143-178.

4. Anderson JR. The adaptive character of thought. Lawrence Erlbaum Associates; 1990.

5. Austin JL. How to do things with words. Clarendon Press; 1962.

6. Baker CL. Bayesian theory of mind: modeling human reasoning about beliefs, desires, goals and social relations. Unpublished doctoral dissertation, Massachusetts Institute of Technology, Cambridge, MA, 2012.

7. Baker CL, Goodman ND, Tenenbaum JB. Theory-based social goal inference. Proceedings of the 13th Annual Conference of the Cognitive Science Society. 2008:1447-1455.

8. Baker CL, Saxe R, Tenenbaum JB. Action understanding as inverse planning. Cognition. 2009;113:329-349.

9. Baker CL, Tenenbaum JB, Saxe RR. Bayesian models of human action understanding. Advances in neural information processing systems. vol. 18. 2006:99-106.

10. Baker CL, Tenenbaum JB, Saxe RR. Goal inference as inverse planning. Proceedings of the 29th Annual Conference of the Cognitive Science Society. 2007:779-787.

11. Barrett H, Todd PM, Miller G, Blythe P. Accurate judgments of intention from motion cues alone: a cross-cultural study. Evol Human Behav. 2005;26(4):313-331.

12. Bello P. Shared representations of belief and their effects on action selection: a preliminary computational cognitive model. Proceedings of the 33rd Annual Conference of the Cognitive Science Society. 2011:2997-3002.

13. Bello P, Bignoli P, Cassimatis NL. Attention and association explain the emergence of reasoning about false beliefs in young children. Proceedings of the Eighth International Conference on Cognitive Modeling. 2007:169-174.

14. Bello P, Cassimatis NL. Developmental accounts of theory-of-mind acquisition: achieving clarity via computational cognitive modeling. Proceedings of the 28th Annual Conference of the Cognitive Science Society. 2006:1014-1019.

15. Bello P, Cassimatis NL. Some unifying principles for computational models of theory-of-mind. Proceedings of the Seventh International Conference on Cognitive Modeling. 2006.

16. Bergen L, Evans OR, Tenenbaum JB. Learning structured preferences. Proceedings of the 32nd Annual Conference of the Cognitive Science Society. 2010.

17. Berthiaume VG, Shultz TR, Onishi KH. A constructivist connectionist model of developmental transitions on false-belief tasks. Cognition. 2013;126(3):441-458.

18. Blythe PW, Todd PM, Miller GF. How motion reveals intention: categorizing social interactions. In: Todd PM, Gigerenzer G, The ABC Research Group, eds. Simple heuristics that make us smart. Oxford University Press; 1999:257-286.

19. Bogdan RJ. Interpreting minds. Bradford Books, MIT Press; 1997.

20. Bui H, Venkatesh S, West G. Policy recognition in the abstract hidden Markov model. J Artif Intell Res. 2002;17:451-499.

21. Camerer CF. Behavioral game theory: experiments in strategic interaction. Princeton University Press; 2003.

22. Camerer CF, Ho T-H, Chong J-K. A cognitive hierarchy model of games. Quart J Econom. 2004;119(3):861-898.

23. Cassimatis NL. Integrating cognitive models based on different computational methods. Proceedings of the 27th Annual Conference of the Cognitive Science Society. 2005.

24. Castelli F, Happe F, Frith U, Frith C. Movement and mind: a functional imaging study of perception and interpretation of complex intentional movement patterns. Neuroimage. 2000;12(3):314-325.

25. Chajewska U, Koller D. Utilities as random variables: density estimation and structure discovery. Proceedings of the 16th Annual Conference on Uncertainty in Artificial Intelligence. 2000:63-71.

26. Chajewska U, Koller D, Ormoneit D. Learning an agent’s utility function by observing behavior. Proceedings of the 18th International Conference on Machine Learning. 2001:35-42.

27. Charniak E, Goldman RP. A Bayesian model of plan recognition. Artif Intell. 1993;64:53-79.

28. Choi J, Kim K-E. Inverse reinforcement learning in partially observable environments. J Mach Learning Res. 2011;12:691-730.

29. Chomsky N. Aspects of the theory of syntax. MIT Press; 1965.

30. Churchland PM. Eliminative materialism and the propositional attitudes. J Philos. 1981;78(2):67-90.

31. Cohen P, Perrault R, Allen J. Beyond question answering. In: Lehnart W, Ringle M, eds. Strategies for natural language processing. Lawrence Erlbaum Associates; 1981:245-274.

32. Cohen PR, Morgan J, Pollack ME, eds. Intentions in communication. MIT Press; 1990.

33. Cohen PR, Perrault CR. Elements of a plan-based theory of speech acts. Cognitive Sci. 1979;3:177-212.

34. Cosmides L, Tooby J. Cognitive adaptations for social exchange. In: Barkow J, Cosmides L, Tooby J, eds. The adapted mind: evolutionary psychology and the generation of culture. Oxford University Press; 1992.

35. Csibra G, Biró S, Koós O, Gergely G. One-year-old infants use teleological representations of actions productively. Cognitive Sci. 2003;27:111-133.

36. Davis LS, Benedikt ML. Computational models of space: Isovists and isovist fields. Comput Graph Image Processing. 1979;11:49-72.

37. Dayan P, Daw ND. Decision theory, reinforcement learning, and the brain. Cognitive Affective Behav Neurosci. 2008;8(4):429-453.

38. Dennett DC. The intentional stance. MIT Press; 1987.

39. Doshi P, Qu X, Goodie A. Decision-theoretic planning in multiagent settings with application to behavioral modeling. In: Sukthankar G, Goldman RP, Geib C, Pynadath DV, Bui HH, eds. Plan, activity, and intent recognition. Waltham, MA: Morgan Kaufmann Publishers; 2014:205-226.

40. Doshi P, Qu X, Goodie A, Young D. Modeling recursive reasoning by humans using empirically informed interactive POMDPs. Proceedings of the Ninth International Conference on Autonomous Agents and Multiagent Systems. 2010.

41. Dvijotham K, Todorov E. Inverse optimal control with linearly-solvable MDPs. Proceedings of the 27th International Conference on Machine Learning. 2010:335-342.

42. Fagin R, Halpern JY, Moses Y, Vardi MY. Reasoning about knowledge. MIT Press; 1995.

43. Frank MC, Goodman ND, Lai P, Tenenbaum JB. Informative communication in word production and word learning. Proceedings of the 31st Annual Conference of the Cognitive Science Society. 2009.

44. Gal Y, Pfeffer A. Reasoning about rationality and beliefs. Proceedings of the Third International Conference on Autonomous Agents and Multiagent Systems. 2004.

45. Gal Y, Pfeffer A. Networks of influence diagrams: a formalism for representing agents beliefs and decision-making processes. J Artif Intell Res. 2008;33:109-147.

46. Gao T, Scholl BJ, McCarthy G. Dissociating the detection of intentionality from animacy in the right posterior superior temporal sulcus. J Neurosci. 2012;32(41):14276-14280.

47. Geib CW, Goldman RP. A probabilistic plan recognition algorithm based on plan tree grammars. Artif Intell. 2009;173(11):1101-1132.

48. Geisler WS. Sequential ideal-observer analysis of visual discrimination. Psychol Rev. 1989;96:267-314.

49. Gergely G, Csibra G. Teleological reasoning in infancy: the naïve theory of rational action teleological reasoning in infancy: the naïve theory of rational action. Trends Cognitive Sci. 2003;7(7):287-292.

50. Gergely G, Nádasdy Z, Csibra G, Biró S. Taking the intentional stance at 12 months of age. Cognition. 1995;56:165-193.

51. Gmytrasiewicz PJ, Doshi P. A framework for sequential planning in multi-agent settings a framework for sequential planning in multi-agent settings. J Artif Intell Res. 2005;24:49-79.

52. Gmytrasiewicz PJ, Durfee EH. A rigorous, operational formalization of recursive modeling. Proceedings of the First International Conference on Multi-agent Systems. 1995.

53. Goldman RP, Geib CW, Miller CA. A new model of plan recognition. Proceedings of the 15th Conference on Uncertainty in Artificial Intelligence. 1999:245-254.

54. Goodman ND, Baker CL, Bonawitz EB, et al. Intuitive theories of mind: a rational approach to false belief. Proceedings of the 28th Annual Conference of the Cognitive Science Society. 2006:1382-1390.

55. Goodman ND, Baker CL, Tenenbaum JB. Cause and intent: social reasoning in causal learning. Proceedings of the 21st Annual Conference of the Cognitive Science Society. 2009:2759-2764.

56. Goodman ND, Stuhlmüller A. Knowledge and implicature: modeling language understanding as social cognition. Top Cognitive Sci. 2013;5:173-184.

57. Gopnik A, Meltzoff AN. Words, thoughts, and theories. MIT Press; 1997.

58. Grice P. Studies in the way of words. Harvard University Press; 1989.

59. Griffiths TL, Tenenbaum JB. Theory-based causal induction. Psychol Rev. 2009;116:661-716.

60. Grosz BJ, Sidner CL. Attention, intentions, and the structure of discourse. Comput Linguist. 1986;12:175-204.

61. Grosz BJ, Sidner CL. Plans for discourse. In: Cohen PR, Morgan J, Pollack ME, eds. Intentions in communication. MIT Press; 1990:417-444.

62. Hamlin JK, Ullman TD, Tenenbaum JB, Goodman ND, Baker CL. The mentalistic basis of core social cognition: experiments in preverbal infants and a computational model. Develop Sci. 2013;16(2):209-226.

63. Hamlin JK, Wynn K. Young infants prefer prosocial to antisocial others. Cognitive Develop. 2011;26(1):30-39.

64. Hamlin JK, Wynn K, Bloom P. Social evaluation by preverbal infants. Nature. 2007;450:557-560.

65. Hamrick JB, Battaglia PW, Tenenbaum JB. Internal physics models guide probabilistic judgments about object dynamics. Proceedings of the 33rd Annual Conference of the Cognitive Science Society. 2011.

66. Hansen EA, Bernstein DS, Zilberstein S. Dynamic programming for partially observable stochastic games. Proceedings of the 19th National Conference on Artificial Intelligence. 2004.

67. Harsanyi JC. Games with incomplete information played by Bayesian players: Part I. the basic model. Manage Sci. 1967;14(3):159-182.

68. Harsanyi JC. Games with incomplete information played by Bayesian players: Part II Bayesian equilibrium points. Manage Sci. 1968;14(5):320-334.

69. Harsanyi JC. Games with incomplete information played by Bayesian players: Part III. The basic probability distribution of the game. Management Sci. 1968;14(7):486-502.

70. Hauskrecht M. Value-function approximations for partially observable Markov decision processes. J Artif Intell Res. 2000;13:33-94.

71. Heider F, Simmel MA. An experimental study of apparent behavior An experimental study of apparent behavior. Am J Psychol. 1944;57:243-249.

72. Ho TH, Camerer C, Weigelt K. Iterated dominance and iterated best response in experimental p-beauty contests. AmEconom Rev. 1998;88:947-969.

73. Jara-Ettinger J, Baker CL, Tenenbaum JB. Learning what is where from social observations. Proceedings of the 34th Annual Conference of the Cognitive Science Society. 2012:515-520.

74. Jern A, Kemp C. Capturing mental state reasoning with influence diagrams. Proceedings of the 33rd Annual Conference of the Cognitive Science Society. 2011.

75. Jern A, Lucas CG, Kemp C. Evaluating the inverse decision-making approach to preference learning. Advances in neural information processing systems. 2011.

76. Kaelbling LP, Littman ML, Cassandra AR. Planning and acting in partially observable stochastic domains planning and acting in partially observable stochastic domains. Artif Intell. 1998;101:99-134.

77. Kahneman D, Slovic P, Tversky A, eds. Judgment under uncertainty: heuristics and biases. Cambridge University Press; 1982.

78. Kautz, H. A Formal Theory of Plan Recognition A formal theory of plan recognition. Unpublished doctoral dissertation, University of Rochester, Rochester, NY; 1987.

79. Kautz H, Allen J. Generalized plan recognition. Proceedings of the Fifth National Conference on Artificial Intelligence. 1986:32-37.

80. Kemp C, Tenenbaum JB. Structured statistical models of inductive reasoning. Psychol Rev. 2009;116(1):20-58.

81. Knill D, Richards W. Perception as Bayesian inference. Cambridge University Press; 1996.

82. Krasnow MM, Truxaw D, Gaulin SJC, New J, Ozono H, Uono S, et al. Cognitive adaptations for gathering-related navigation in humans. Evol Human Behav. 2011;32:1-12.

83. Lee SM, Gao T, McCarthy G. Attributing intentions to random motion engages the posterior superior temporal sulcus. Soc Cogn Affect Neurosci. 2014;9(1):81-87.

84. Lewis D. Convention: a philosophical study. Harvard University Press; 1969.

85. Liao L, Fox D, Kautz H. Learning and inferring transportation routines. Proceedings of the 19th National Conference on Artificial Intelligence. 2004:348-353.

86. Litman DJ, Allen JF. A plan recognition model for subdialogues in conversations. Cognitive Sci. 1987;11:163-200.

87. Littman ML. Markov games as a framework for multi-agent reinforcement learning. Proceedings of the 11th International Conference on Machine Learning. 1994:157-163.

88. Lovejoy WS. Computationally feasible bounds for partially observed Markov decision processes. Oper Res. 1991;39(1):162-175.

89. Lucas C, Griffiths TL, Xu F, Fawcett C. A rational model of preference learning and choice prediction by children. Advances in neural information processing systems 21. 2009.

90. Luo Y. Three-month-old infants attribute goals to a non-human agent. Develop Sci. 2011;14(2):453-460.

91. Luo Y, Baillargeon R. Toward a mentalistic account of early psychological reasoning. Curr Direct Psychol Sci. 2010;19(5):301-307.

92. Marr D. Vision. Freeman Publishers; 1982.

93. Milch B, Koller D. Probabilistic models for agents’ beliefs and decisions. Proceedings of the 16th Conference on Uncertainty in Artificial Intelligence. 2000:389-396.

94. Morariu VI, Prasad VSN, Davis LS. Human activity understanding using visibility context. IEEE/RSJ IROS workshop: from sensors to human spatial concepts; 2007.

95. Murphy, KP. Dynamic Bayesian Networks: Representation, Inference and Learning. Unpublished doctoral dissertation, Massachusetts Institute of Technology; 2002.

96. Neu G, Szepesvári C. Apprenticeship learning using inverse reinforcement learning and gradient methods. Proceedings of the 23rd Conference on Uncertainty in Artificial Intelligence. 2007.

97. Ng AY, Russell S. Algorithms for inverse reinforcement learning. Proceedings of the 17th International Conference on Machine Learning. 2000:663-670.

98. Ong SCW, Png SW, Hsu D, Lee WS. POMDPs for robotic tasks with mixed observability. Robotics: Sci Syst. 2009;5.

99. Onishi KH, Baillargeon R. Do 15-month-old infants understand false beliefs? Science. 2005;308(5719):255-258.

100. Oztop E, Wolpert D, Kawato M. Mental state inference using visual control parameters. Cognitive Brain Res. 2005;22:129-151.

101. Pantelis PC, Baker CL, Cholewiak SA, Sanik K, Weinstein A, Wu C, et al. Inferring the intentional states of autonomous virtual agents. Cognition. 2014;130:360-379.

102. Perrault CR, Allen JF. A plan-based analysis of indirect speech acts. Comput Linguist. 1980;6(3–4):167-182.

103. Pynadath DV, Marsella SC. Psychsim: modeling theory of mind with decision-theoretic agents. Proceedings of the 21st International Joint Conference on Artificial Intelligence. 2005.

104. Pynadath DV, Wellman MP. Probabilistic state-dependent grammars for plan recognition. Proceedings of the 16th Conference on Uncertainty in Artificial Intelligence. 2000.

105. Rabiner LR. A tutorial on hidden Markov models and selected applications in speech recognition. Proc IEEE. 1989;77(2):257-286.

106. Ramachandran D, Amir E. Bayesian inverse reinforcement learning. Proceedings of the 20th International Joint Conference on Artificial Intelligence. 2007.

107. Ramirez M, Geffner H. Probabilistic plan recognition using off-the-shelf classical planners. Proceedings of the 25th National Conference on Artificial Intelligence. 2010.

108. Ramirez M, Geffner H. Goal recognition over POMDPs: inferring the intention of a POMDP agent. Proceedings of the 27th International Joint Conference on Artificial Intelligence. 2011.

109. Rao RPN, Shon AP, Meltzoff AN. A Bayesian model of imitation in infants and robots. In: Dautenhahn K, Nehaniv C C, eds. Imitation and social learning in robots, humans, and animals. Cambridge University Press; 2007.

110. Saxe R. Against simulation: the argument from error. Trends Cognitive Sci. 2005;94.

111. Schank RC, Abelson RP. Scripts, plans, goals, and understanding: an inquiry into human knowledge structures. Lawrence Erlbaum Associates; 1977.

112. Schmidt CF, Marsella SC. Planning and plan recognition from a computational point of view. In: Whiten A, ed. Natural theories of mind: evolution, development, and simulation of everyday mindreading. Basil Blackwell; 1991:109-126.

113. Schmidt CF, Sridharan NS, Goodson JL. The plan recognition problem: an intersection of psychology and artificial intelligence. Artif Intell. 1978;11:45-83.

114. Schultz J, Friston K, Wolpert DM, Frith CD. Activation in posterior superior temporal sulcus parallels parameter inducing the percept of animacy. Neuron. 2005;45:625-635.

115. Schultz TR. From agency to intention: a rule-based, computational approach. In: Whiten A, ed. Natural theories of mind: evolution, development, and simulation of everyday mindreading. Basil Blackwell; 1991:79-95.

116. Searle JR. Speech acts: an essay in the philosophy of language. Cambridge University Press; 1969.

117. Searle JR. Intentionality: an essay in the philosophy of mind. Cambridge University Press; 1983.

118. Searle JR. Collective intentions and actions. In: Cohen PR, Morgan J, Pollack ME, eds. Intentions in communication. MIT Press; 1990:401-415.

119. Shafto P, Goodman ND. Teaching games: statistical sampling assumptions for learning in pedagogical situations. Proceedings of the 30th Annual Conference of the Cognitive Science Society. 2008.

120. Shafto P, Kemp C, Bonawitz EB, Coley JD, Tenenbaum JB. Inductive reasoning about causally transmitted properties. Cognition. 2008;109:175-192.

121. Si M, Marsella SC, Pynadath DV. Modeling appraisal in theory of mind reasoning. J Autonomous Agents Multi Agent Syst. 2010;20(1):14-31.

122. Stahl DO, Wilson PW. On players models of other players: theory and experimental evidence. Games Econom Behav. 1995;10:218-254.

123. Stuhlmüller A, Goodman ND. Reasoning about reasoning by nested conditioning: modeling theory of mind with probabilistic programs. J Cognitive Syst Res. 2013.

124. Sutton RS, Barto AG. Reinforcement learning: an introduction. MIT Press; 1998.

125. Tauber S, Steyvers M. Using inverse planning and theory of mind for social goal inference. Proceedings of the 33rd Annual Conference of the Cognitive Science Society. 2011.

126. Tenenbaum JB, Griffiths TL, Kemp C. Theory-based Bayesian models of inductive learning and reasoning. Trends Cognitive Sci. 2006;10(7):309-318.

127. Thrun S, Montemerlo M, Dahlkamp H, Stavens D, Aron A, Diebel J, et al. Stanley: the robot that won the DARPA grand challenge. J Field Robot. 2006;23(9):661-692.

128. Tremoulet PD, Feldman J. Perception of animacy from the motion of a single object. Perception. 2000;29:943-951.

129. Tremoulet PD, Feldman J. The influence of spatial context and the role of intentionality in the interpretation of animacy from motion. Percept Psychophys. 2006;29:943-951.

130. Ullman TD, Baker CL, Macindoe O, Evans O, Goodman ND, Tenenbaum JB. Help or hinder. Advances in neural information processing systems 22. 2009:1874-1882.

131. Vail DL, Veloso MM, Lafferty JD. Conditional random fields for activity recognition conditional random fields for activity recognition. Proceedings of the Sixth International Conference on Autonomous Agents and Multiagent Systems. 2007.

132. Van Overwalle F. Infants’ teleological and belief inference: a recurrent connectionist approach to their minimal representational and computational requirements. Neuroimage. 2010;52:1095-1108.

133. Verma D, Rao R. Goal-based imitation as probabilistic inference over graphical models. Advances in neural information processing systems. vol. 18. 2006:1393-1400.

134. Wahl S, Spada H. Children’s reasoning about intentions, beliefs and behaviour. Cognitive Sci Quart. 2000:15-34.

135. Waugh K, Ziebart BD, Bagnell JA. Computational rationalization: the inverse equilibrium problem. Proceedings of the 28th International Conference on Machine Learning. 2011.

136. Wellman HM. The child’s theory of mind. MIT Press; 1990.

137. Wellman HM, Bartsch K. Young children’s reasoning about beliefs. Cognition. 1988;30:239-277.

138. Wellman HM, Gelman SA. Cognitive development: foundational theories of core domains. Annu Rev Psychol. 1992;43:337-375.

139. Whiten A, ed. Natural theories of mind: evolution, development, and simulation of everyday mindreading. Basil Blackwell; 1991.

140. Wimmer H, Perner J. Beliefs about beliefs: representation and constraining function of wrong beliefs in young children’s understanding of deception. Cognition. 1983;13(1):103-128.

141. Wolpert DM, Doya K, Kawato M. A unifying computational framework for motor control and social interaction. Philos Trans R Soc Lond B. 2003;358:593-602.

142. Woodward AL. Infants selectively encode the goal object of an actor’s reach. Cognition. 1998;69:1-34.

143. Yoshida W, Dolan RJ, Friston KJ. Game theory of mind. PLoS Comput Biol. 2008;4(12):1-14.

144. Yoshida W, Seymour B, J Friston K, Dolan RJ. Neural mechanisms of belief inference during cooperative games. J Neurosci. 2010;30(32):10744-10751.

145. Zacks JM. Using movement and intentions to understand simple events. Cognitive Sci. 2004;28:979-1008.

146. Zettlemoyer LS, Milch B, Kaelbling LP. Multi-agent filtering with infinitely nested beliefs. Advances in neural information processing systems. 21. 2009.

147. Ziebart BD, Bagnell JA, Dey AK. Modeling interaction via the principle of maximum causal entropy. Proceedings of the 27th International Conference on Machine Learning. 2010.

1 These are the so-called “propositional attitudes” central to classic discussions of ToM and “folk–psychology” (e.g., see Wimmer and Perner [140], Dennett [38] and Churchland [30]). This chapter focuses on beliefs and desires; in general, ToM may encompass a broader class of mental states (e.g., including emotions), although the extent to which the propositional content of these may be reducible to beliefs and desires is debatable (e.g., see Searle [117]).

2 The first of these is necessary to capture belief updating on the basis of worlds with different dynamics. For example, suppose the agent is at a parking spot, and believes a truck to be there. If the agent does not transition to the “Finished” state on choosing the “Eat” action, it can instantly deduce that no truck is there, even without receiving the corresponding observation signal (assuming “Finished” state transitions are deterministic when trucks are present).

3 Analyses based on sophisticated notions of common knowledge described by Lewis [84] and Fagin et al. [42] and joint intention described by Searle [118] and Grosz and Sidner [61], are outside of the scope of this chapter.

4 These frameworks depart from the keyhole plan-recognition setting considered here, instead performing intended plan recognition.