Algorithms Third Edition in C++ Part 5. Graph Algorithms (2006)
CHAPTER EIGHTEEN
Graph Search
18.4 Properties of DFS Forests
As noted in Section 18.2, the trees that describe the recursive structure of DFS function calls give us the key to understanding how DFS operates. In this section, we examine properties of the algorithm by examining properties of DFS trees.
If we add external nodes to the DFS tree to record the moments when we skipped recursive calls for vertices that had already been visited, we get the compact representation of the dynamics of DFS illustrated in Figure 18.9. This representation is worthy of careful study. The tree is a representation of the graph, with a vertex corresponding to each graph vertex and an edge corresponding to each graph edge. We can choose to show the two representations of the edge that we process (one in each direction), as shown in the left part of the figure, or just one representation of each edge, as shown in the center and right parts of the figure. The former is useful in understanding that the algorithm processes each and every edge; the latter is useful in understanding that the DFS tree is simply another graph representation. Traversing the internal nodes of the tree in preorder gives the vertices in the order in which DFS visits them; moreover, the order in which we visit the edges of the tree as we traverse it in preorder is the same as the order in which DFS examines the edges of the graph.
Indeed, the DFS tree in Figure 18.9 contains the same information as the trace in Figure 18.5 or the step-by-step illustration of Trémaux traversal in Figures 18.2 and 18.3. Edges to internal nodes represent edges (passages) to unvisited vertices (intersections), edges to external nodes represent occasions where DFS checks edges that lead to previously visited vertices (intersections), and shaded nodes represent edges to vertices for which a recursive DFS is in progress (when we open a door to a passage where the door at the other end is already open). With these interpretations, a preorder traversal of the tree tells the same story as that of the detailed maze-traversal scenario.
To study more intricate graph properties, we classify the edges in a graph according to the role that they play in the search. We have two distinct edge classes:
• Edges representing a recursive call (tree edges)
• Edges connecting a vertex with an ancestor in its DFS tree that is not its parent (back edges)
When we study DFS trees for digraphs in Chapter 19, we examine other types of edges, not just to take the direction into account, but also because we can have edges that go across the tree, connecting nodes that are neither ancestors nor descendants in the tree.
Since there are two representations of each graph edge that each correspond to a link in the DFS tree, we divide the tree links into four classes, using the preorder numbers and the parent links (in the ord and st arrays, respectively) that our DFS code computes. We refer to a link from v to w in a DFS tree that represents a tree edge as
• A tree link if w is unmarked
• A parent link if st[w] is v
and a link from v to w that represents a back edge as
• A back link if ord[w] < ord[v]
• A down link if ord[w] > ord[v]
Each tree edge in the graph corresponds to a tree link and a parent link in the DFS tree, and each back edge in the graph corresponds to a back link and a down link in the DFS tree.
In the graphical DFS representation illustrated in Figure 18.9, tree links point to unshaded circles, parent links point to shaded circles, back links point to unshaded squares, and down links point to shaded squares. Each graph edge is represented either as one tree link and one parent link or as one down link and one back link. These classifications are tricky and worthy of study. For example, note that even though parent links and back links both point to ancestors in the tree, they are quite different: A parent link is just the other representation of a tree link, but a back link gives us new information about the structure of the graph.
Figure 18.10 DFS trace (tree link classifications)

This version of Figure 18.5 shows the classification of the DFS tree link corresponding to each graph edge representation encountered. Tree edges (which correspond to recursive calls) are represented as tree links on the first encounter and parent links on the second encounter. Back edges are back links on the first encounter and down links on the second encounter.
The definitions just given provide sufficient information to distinguish among tree, parent, back, and down links in a DFS class implementation. Note that parent links and back links both have ord[w] < ord[v], so we have also to know that st[w] is not v to know that v-w is a back link. Figure 18.10 depicts the result of printing out the classification of the DFS tree link for each graph edge as that edge is encountered during a sample DFS. It is yet another complete representation of the basic search process that is an intermediate step between Figure 18.5 and Figure 18.9.
The four types of tree links correspond to the four different ways in which we treat edges during a DFS, as described (in maze-exploration terms) at the end of Section 18.1. A tree link corresponds to DFS encountering the first of the two representations of a tree edge, leading to a recursive call (to as-yet-unseen vertices); a parent link corresponds to DFS encountering the other representation of the tree edge (when going through the adjacency list on that first recursive call) and ignoring it. A back link corresponds to DFS encountering the first of the two representations of a back edge, which points to a vertex for which the recursive search function has not yet completed; a down link corresponds to DFS encountering a vertex for which the recursive search has completed at the time that the edge is encountered. In Figure 18.9, tree links and back links connect unshaded nodes, represent the first encounter with the corresponding edge, and constitute a representation of the graph; parent links and down links go to shaded nodes and represent the second encounter with the corresponding edge.
We have considered this tree representation of the dynamic characteristics of recursive DFS in detail not just because it provides a complete and compact description of both the graph and the operation of the algorithm, but also because it gives us a basis for understanding numerous important graph-processing algorithms. In the remainder of this chapter, and in the next several chapters, we consider a number of examples of graph-processing problems that draw conclusions about a graph’s structure from the DFS tree.
Search in a graph is a generalization of tree traversal. When invoked on a tree, DFS is precisely equivalent to recursive tree traversal; for graphs, using it corresponds to traversing a tree that spans the graph
Figure 18.11 DFS forest
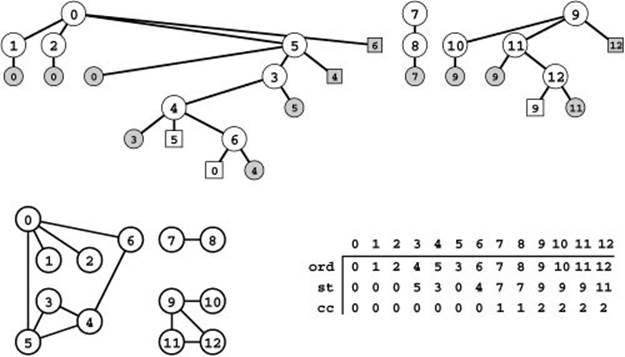
The DFS forest at the top represents a DFS of an adjacency-matrix representation of the graph at the bottom right. The graph has three connected components, so the forest has three trees. The ord vector is a preorder numbering of the nodes in the tree (the order in which they are examined by the DFS) and the st vector is a parent-link representation of the forest. The cc vector associates each vertex with a connected-component index (see Program 18.4). As in Figure 18.9, edges to circles are tree edges; edges that go to squares are back edges; and shaded nodes indicate that the incident edge was encountered earlier in the search, in the other direction.
and that is discovered as the search proceeds. As we have seen, the particular tree traversed depends on how the graph is represented. DFS corresponds to preorder tree traversal. In Section 18.6, we examine the graph-searching analog to level-order tree traversal and explore its relationship to DFS; in Section 18.7, we examine a general schema that encompasses any traversal method.
When traversing graphs with DFS, we have been using the ord vector to assign preorder numbers to the vertices in the order that we start processing them. We can also assign postorder numbers to vertices, in the order that we finish processing them (just before returning from the recursive search function). When processing a graph, we do more than simply traverse the vertices—as we shall see, the preorder and postorder numbering give us knowledge about global graph properties that helps us to accomplish the task at hand. Preorder numbering suffices for the algorithms that we consider in this chapter, but we use postorder numbering in later chapters.
We describe the dynamics of DFS for a general undirected graph with a DFS forest that has one DFS tree for each connected component. An example of a DFS forest is illustrated in Figure 18.11.
With an adjacency-lists representation, we visit the edges connected to each vertex in an order different from that for the adjacency-matrix representation, so we get a different DFS forest, as illustrated in Figure 18.12. DFS trees and forests are graph representations that describe not only the dynamics of DFS but also the internal representation
Figure 18.12 Another DFS forest
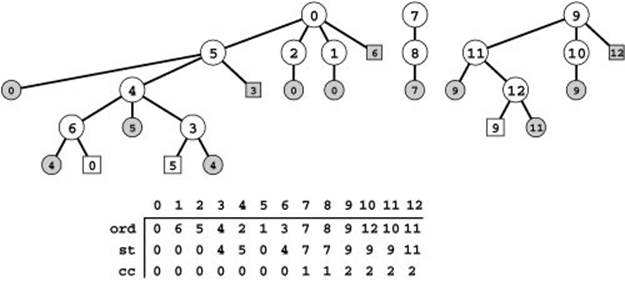
This forest describes depth-first search of the same graph as Figure 18.11, but using an adjacency-list representation, so the search order is different because it is determined by the order that nodes appear in adjacency lists. Indeed, the forest itself tells us that order: it is the order in which children are listed for each node in the tree. For instance, the nodes on 0’s adjacency list were found in the order 521 6, the nodes on 4’s list are in the order 653, and so forth. As before, all vertices and edges in the graph are examined during the search, in a manner that is precisely described by a preorder walk of the tree. The ord and st vectors depend upon the graph representation and the search dynamics and are different from Figure 18.11, but the vector cc depends on graph properties and is the same.
of the graph. For example, by reading the children of any node in Figure 18.12 from left to right, we see the order in which they appear on the adjacency list of the vertex corresponding to that node. We can have many different DFS forests for the same graph—each ordering of nodes on adjacency lists leads to a different forest.
Details of the structure of a particular forest inform our understanding of how DFS operates for particular graphs, but most of the important DFS properties that we consider depend on graph properties that are independent of the structure of the forest. For example, the forests in Figures 18.11and 18.12 both have three trees (as would any other DFS forest for the same graph) because they are just different representations of the same graph, which has three connected components. Indeed, a direct consequence of the basic proof that DFS visits all the nodes and edges of a graph (see Properties 18.2 through 18.4) is that the number of connected components in the graph is equal to the number of trees in the DFS forest. This example illustrates the basis for our use of graph search throughout the book: A broad variety of graph-processing class implementations are based on learning graph properties by processing a particular graph representation (a forest corresponding to the search).
Potentially, we could analyze DFS tree structures with the goal of improving algorithm performance. For example, should we attempt to speed up an algorithm by rearranging the adjacency lists before starting the search? For many of the important classical DFS-based algorithms, the answer to this question is no, because they are optimal—their worst-case running time depends on neither the graph structure nor the order in which edges appear on the adjacency lists (they essentially process each edge exactly once). Still, DFS forests have a characteristic structure that is worth understanding because it distinguishes them from other fundamental search schema that we consider later in this chapter.
Figure 18.13 shows a DFS tree for a larger graph that illustrates the basic characteristics of DFS search dynamics. The tree is tall and thin, and it demonstrates several characteristics of the graph being searched and of the DFS process.
• There exists at least one long path that connects a substantial fraction of the nodes.
• During the search, most vertices have at least one adjacent vertex that we have not yet seen.
• We rarely make more than one recursive call from any node.
• The depth of the recursion is proportional to the number of vertices in the graph.
This behavior is typical for DFS, though these characteristics are not guaranteed for all graphs. Verifying facts of this kind for graph models of interest and various types of graphs that arise in practice requires detailed study. Still, this example gives an intuitive feel for DFS-based algorithms that is often borne out in practice. Figure 18.13 and similar figures for other graph-search algorithms (see Figures 18.24 and 18.29) help us understand differences in their behavior.
Exercises
18.15 Draw the DFS forest that results from a standard adjacency-matrix DFS of the graph
3-7 1-4 7-8 0-5 5-2 3-8 2-9 0-6 4-9 2-6 6-4.
18.16 Draw the DFS forest that results from a standard adjacency-lists DFS of the graph
3-7 1-4 7-8 0-5 5-2 3-8 2-9 0-6 4-9 2-6 6-4.
18.17 Write a DFS trace program to produce output that classifies each of the two representations of each graph edge as corresponding to a tree, parent, back, or down link in the DFS tree, in the style of Figure 18.10.
• 18.18 Write a program that computes a parent-link representation of the full DFS tree (including the external nodes), using an vector of E integers between 0 and V − 1. Hint: The first V entries in the vector should be the same as those in the st vector described in the text.
Figure 18.13 Depth-first search
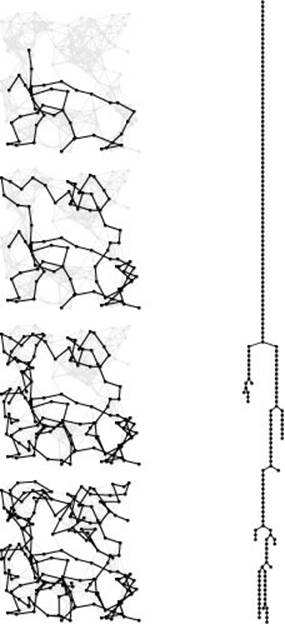
This figure illustrates the progress of DFS in a random Euclidean near-neighbor graph (left). The figures show the DFS tree vertices and edges in the graph as the search progresses through 1/4, 1/2, 3/4, and all of the vertices (top to bottom). The DFS tree (tree edges only) is shown at the right. As is evident from this example, the search tree for DFS tends to be quite tall and thin for this type of graph (as it is for many other types of graphs commonly encountered in practice). We normally find a vertex nearby that we have not seen before.
• 18.19 Instrument the spanning-forest DFS class (Program 18.3) by adding member functions (and appropriate private data members) that return the height of the tallest tree in the forest, the number of back edges, and the percentage of edges processed to see every vertex.
• 18.20 Run experiments to determine empirically the average values of the quantities described in Exercise 18.19 for graphs of various sizes, drawn from various graph models (see Exercises 17.64–76).
• 18.21 Write a function that builds a graph by inserting edges from a given vector into an initially empty graph, in random order. Using this function with an adjacency-lists implementation of the graph ADT, run experiments to determine empirically properties of the distribution of the quantities described in Exercise 18.19 for all the adjacency-lists representations of large sample graphs of various sizes, drawn from various graph models (see Exercises 17.64–76).