Algorithms Third Edition in C++ Part 5. Graph Algorithms (2006)
CHAPTER EIGHTEEN
Graph Search
18.5 DFS Algorithms
Regardless of the graph structure or the representation, any DFS forest allows us to identify edges as tree or back edges and gives us dependable insights into graph structure that allow us to use DFS as a basis for solving numerous graph-processing problems. We have already seen, in Section 17.7, basic examples related to finding paths. In this section, we consider DFS-based ADT function implementations for these and other typical problems; in the remainder of this chapter and in the next several chapters, we look at numerous solutions to much more difficult problems.
Cycle detection Does a given graph have any cycles? (Is the graph a forest?) This problem is easy to solve with DFS because any back edge in a DFS tree belongs to a cycle consisting of the edge plus the tree path connecting the two nodes (see Figure 18.9). Thus, we can use DFS immediately to check for cycles: A graph is acyclic if and only if we encounter no back (or down!) edges during a DFS. For example, to test this condition in Program 18.1, we simply add an else clause to the if statement to test whether t is equal to v. If it is, we have just encountered the parent link w-v (the second representation of the edge v-w that led us to w). If it is not, w-t completes a cycle with the edges from t down to w in the DFS tree. Moreover, we do not need to examine all the edges: We know that we must find a cycle or finish the search without finding one before examining V edges, because any graph with V or more edges must have a cycle. Thus, we can test whether a graph is acyclic in time proportional to V with the adjacency-lists representation, although we may need time proportional to V2 (to find the edges) with the adjacency-matrix representation.
Simple path Given two vertices, is there a path in the graph that connects them? We saw in Section 17.7 that a DFS class that can solve this problem in linear time is easy to devise.
Simple connectivity As discussed in Section 18.3, we determine whether or not a graph is connected whenever we use DFS, in linear time. Indeed, our graph-search strategy is based upon calling a search function for each connected component. In a DFS, the graph is connected if and only if the graph-search function calls the recursive DFS function just once (see Program 18.2). The number of connected components in the graph is precisely the number of times that the recursive function is called from GRAPHsearch, so we can find the number of connected components by simply keeping track of the number of such calls.
More generally, Program 18.4 illustrates a DFS class that supports constant-time connectivity queries after a linear-time preprocessing step in the constructor. It visits vertices in the same order as does Program 18.3. The recursive function uses a vertex as its second argument instead of an edge, since it does not need to know the identity of the parent. Each tree in the DFS forest identifies a connected component, so we arrange to decide quickly whether two vertices are in the same component by including a vertex-indexed vector in the graph representation, to be filled in by a DFS and accessed for connectivity queries. In the recursive DFS function, we assign the current value of the component counter to the entry corresponding to each vertex visited. Then, we know that two vertices are in the same component if and only if their entries in this vector are equal. Again, note that this vector reflects structural properties of the graph, rather than artifacts of the graph representation or of the search dynamics.
Program 18.4 typifies the basic approach that we shall use in addressing numerous graph-processing tasks. We develop a task-specific class so that clients can create objects to perform the task. Typically, we invest preprocessing time in the constructor to compute private data about relevant structural graph properties that help us to provide efficient implementations of public query functions. In this case, the constructor
Program 18.4 Graph connectivity
The CC constructor computes, in linear time, the number of connected components in a graph and stores a component index associated with each vertex in the private vertex-indexed vector id. Clients can use a CC object to find the number of connected components (count) or test whether any pair of vertices are connected (connect), in constant time.
template <class Graph> class CC
{ const Graph &G;
int ccnt;
vector <int> id;
void ccR(int w)
{
id[w] = ccnt;
typename Graph::adjIterator A(G, w);
for (int v = A.beg(); !A.end(); v = A.nxt())
if (id[v] == -1) ccR(v);
}
public:
CC(const Graph &G) : G(G), ccnt(0), id(G.V(), -1)
{
for (int v = 0; v < G.V(); v++)
if (id[v] == -1) { ccR(v); ccnt++; }
}
int count() const { return ccnt; }
bool connect(int s, int t) const
{ return id[s] == id[t]; }
};
preprocesses with a (linear-time) DFS and keeps a private data member (the vertex-indexed vector id) that allows it to answer connectivity queries in constant time. For other graph-processing problems, our constructors might use more space, preprocessing time, or query time. As usual, our focus is on minimizing such costs, although doing so is often challenging. For example, much of Chapter 19 is devoted to solving the connectivity problem for digraphs, where achieving linear time preprocessing and constant query time, as in Program 18.4, is an elusive goal.
Program 18.5 Two-way Euler tour
This DFS class prints each edge twice, once in each orientation, in a two-way–Euler-tour order. We go back and forth on back edges and ignore down edges (see text). It is derived from the SEARCH base class in Program 18.2.
template <class Graph>
class EULER : public SEARCH<Graph>
{
void searchC(Edge e)
{ int v = e.v, w = e.w;
ord[w] = cnt++;
cout << “-” << w;
typename Graph::adjIterator A(G, w);
for (int t = A.beg(); !A.end(); t = A.nxt())
if (ord[t] == -1) searchC(Edge(w, t));
else if (ord[t] < ord[v])
cout << “-” << t << “-” << w;
if (v != w) cout << “-” << v; else cout << endl;
}
public:
EULER(const Graph &G) : SEARCH<Graph>(G)
{ search(); }
};
How does the DFS-based solution for graph connectivity in Program 18.4 compare with the union-find approach that we considered in Chapter 1 for the problem of determining whether a graph is connected, given an edge list? In theory, DFS is faster than union-find because it provides a constant-time guarantee, which union- find does not; in practice, this difference is negligible, and union-find is faster because it does not have to build a full representation of the graph. More important, union-find is an online algorithm (we can check whether two vertices are connected in near-constant time at any point), whereas the DFS solution preprocesses the graph to answer connectivity queries in constant time. Therefore, for example, we prefer union-find when determining connectivity is our only task or when we have a large number
Figure 18.14 A two-way Euler tour
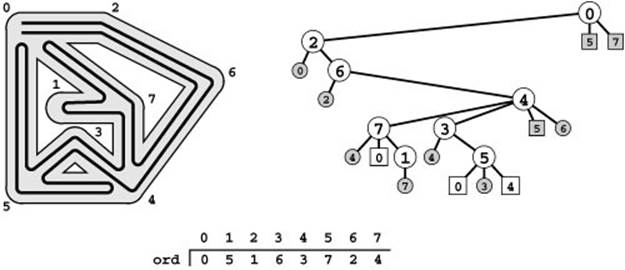
Depth-first search gives us a way to explore any maze, traversing both passages in each direction. We modify Trémaux exploration to take the string with us wherever we go and take a back-and-forth trip on passages without any string in them that go to intersections that we have already visited. This figure shows a different traversal order than shown in Figures 18.2 and 18.3, primarily so that we can draw the tour without crossing itself. This ordering might result, for example, if the edges were processed in some different order when building an adjacency-lists representation of the graph; or, we might explicitly modify DFS to take the geometric placement of the nodes into account (see Exercise 18.26). Moving along the lower track leading out of 0, we move from 0 to 2 to 6 to 4 to 7, then take a trip from 7 to 0 and back because ord[0] is less than ord[7]. Then we go to 1, back to 7, back to 4, to 3, to 5, from 5 to 0 and back, from 5 to 4 and back, back to 3, back to 4, back to 6, back to 2, and back to 0. This path may be obtained by a recursive pre- and postorder walk of the DFS tree (ignoring the shaded vertices that represent the second time we encounter the edges) where we print out the vertex name, recursively visit the subtrees, then print out the vertex name again.
of queries intermixed with edge insertions but may find the DFS solution more appropriate for use in a graph ADT because it makes efficient use of existing infrastructure. Neither approach handles efficiently huge numbers of intermixed edge insertions, edge deletions, and connectivity queries; both require a separate DFS to compute the path. These considerations illustrate the complications that we face when analyzing graph algorithms; we explore them in detail in Section 18.9.
Two-way Euler tour Program 18.5 is a DFS-based class for finding a path that uses all the edges in a graph exactly twice—once in each direction (see Section 17.7). The path corresponds to a Trémaux exploration in which we take our string with us everywhere that we go, check for the string instead of using lights (so we have to go down the passages that lead to intersections that we have already visited), and first arrange to go back and forth on each back link (the first time that we encounter each back edge), then ignore down links (the second time that we encounter each back edge). We might also choose to ignore the back links (first encounter) and to go back and forth on down links (second encounter) (see Exercise 18.25).
Spanning forest Given a connected graph with V vertices, find a set of V − 1 edges that connects the vertices. If the graph has C connected components, find a spanning forest (with V - C edges). We have already seen a DFS class that solves this problem: Program 18.3.
Vertex search How many vertices are in the same connected component as a given vertex? We can solve this problem easily by starting a DFS at the vertex and counting the number of vertices marked. In a dense graph, we can speed up the process considerably by stopping the DFS after we have marked V vertices—at that point, we know that
Figure 18.15 Two-coloring a DFS tree
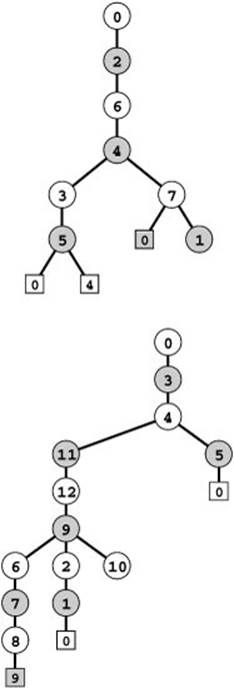
To two-color a graph, we alternate colors as we move down the DFS tree, then check the back edges for inconsistencies. In the tree at the top, a DFS tree for the sample graph illustrated in Figure 18.9, the back edges 5-4 and 7-0 prove that the graph is not two-colorable because of the odd-length cycles 4-3-5-4 and 0-2-6-4-7-0, respectively. In the tree at the bottom, a DFS tree for the bipartite graph illustrated in Figure 17.5, there are no such inconsistencies, and the indicated shading is a two-coloring of the graph.
Program 18.6 Two-colorability (bipartiteness)
The constructor in this DFS class sets OK to true if and only if it is able to assign the values 0 or 1 to the vertex-indexed vector vc such that, for each graph edge v-w, vc[v] and vc[w] are different.
no edge will take us to a vertex that we have not yet seen, so we will be ignoring all the rest of the edges. This improvement is likely to allow us to visit all vertices in time proportional to V log V, not E (see Section 18.8).
Two-colorability, bipartiteness, odd cycle Is there a way to assign one of two colors to each vertex of a graph such that no edge connects two vertices of the same color? Is a given graph bipartite (see Section 17.1)? Does a given graph have a cycle of odd length? These three problems are all equivalent: The first two are different nomenclature for the same problem; any graph with an odd cycle is clearly not two-colorable, and Program 18.6 demonstrates that any graph that is free of odd cycles can be two-colored. The program is a DFS-based ADT function implementation that tests whether a graph is bipartite, two-colorable, and free of odd cycles. The recursive function is an outline for a proof by induction that the program two-colors any graph with no odd cycles (or finds an odd cycle as evidence that a graph that is not free of odd cycles cannot be two-colored). To two-color a graph with a given color assigned to a vertex v, two-color the remaining graph, assigning the other color to each vertex adjacent to v. This process is equivalent to assigning alternate colors on levels as we proceed down the DFS tree, checking back edges for consistency in the coloring, as illustrated in Figure 18.15. Any back edge connecting two vertices of the same color is evidence of an odd cycle.
These basic examples illustrate ways in which DFS can give us insight into the structure of a graph. They also demonstrate that we can learn various important graph properties in a single linear-time sweep through the graph, where we examine every edge twice, once in each direction. Next, we consider an example that shows the utility of DFS in discovering more intricate details about the graph structure, still in linear time.
Exercises
• 18.22 Implement a DFS-based cycle-testing class that preprocesses a graph in time proportional to V in the constructor to support public member functions for detecting whether a graph has any cycles and for printing a cycle if one exists.
18.23 Describe a family of graphs with V vertices for which a standard adjacency-matrix DFS requires time proportional to V2 for cycle detection.
• 18.24 Implement the graph-connectivity class of Program 18.4 as a derived graph-search class, like Program 18.3.
• 18.25 Specify a modification to Program 18.5 that will produce a two-way Euler tour that does the back-and-forth traversal on down edges instead of back edges.
• 18.26 Modify Program 18.5 such that it always produces a two-way Euler tour that, like the one in Figure 18.14, can be drawn such that it does not cross itself at any vertex. For example, if the search in Figure 18.14 were to take the edge 4-3 before the edge 4-7, then the tour would have to cross itself; your task is to ensure that the algorithm avoids such situations.
18.27 Develop a version of Program 18.5 that sorts the edges of a graph in order of a two-way Euler tour. Your program should return a vector of edges that corresponds to a two-way Euler tour.
18.28 Prove that a graph is two-colorable if and only if it contains no odd cycle. Hint: Prove by induction that Program 18.6 determines whether or not any given graph is two-colorable.
• 18.29 Explain why the approach taken in Program 18.6 does not generalize to give an efficient method for determining whether a graph is three-colorable.
18.30 Most graphs are not two-colorable, and DFS tends to discover that fact quickly. Run empirical tests to study the number of edges examined by Program 18.6, for graphs of various sizes, drawn from various graph models (see Exercises 17.64–76).
• 18.31 Prove that every connected graph has a vertex whose removal will not disconnect the graph, and write a DFS function that finds such a vertex. Hint: Consider the leaves of the DFS tree.
18.32 Prove that every graph with more than one vertex has at least two vertices whose removal will not increase the number of connected components.