Algorithms Third Edition in C++ Part 5. Graph Algorithms (2006)
CHAPTER NINETEEN
Digraphs and DAGs
19.8 Strong Components in Digraphs
Undirected graphs and DAGs are both simpler structures than general digraphs because of the structural symmetry that characterizes the reachability relationships among the vertices: In an undirected graph, if there is a path from s to t, then we know that there is also a path from t to s; in a DAG, if there is a directed path from s to t, then we know that there is no directed path from t to s. For general digraphs, knowing that t is reachable from s gives no information about whether s is reachable from t.
To understand the structure of digraphs, we consider strong connectivity, which has the symmetry that we seek. If s and t are strongly connected (each reachable from the other), then, by definition, so are t and s. As discussed in Section 19.1, this symmetry implies that the vertices of the digraph divide into strong components, which consist of mutually reachable vertices. In this section, we discuss three algorithms for finding the strong components in a digraph.
We use the same interface as for connectivity in our general graph-searching algorithms for undirected graphs (see Program 18.4). The goal of our algorithms is to assign component numbers to each vertex in a vertex-indexed vector, using the labels 0, 1, [triangleright][triangleright][triangleright], for the strong components. The highest number assigned is one less than the number of strong components, and we can use the component numbers to provide a constant-time test of whether two vertices are in the same strong component.
A brute-force algorithm to solve the problem is simple to develop. Using an abstract–transitive-closure ADT, check every pair of vertices s and t to see whether t is reachable from s and s is reachable from t. Define an undirected graph with an edge for each such pair: The connected components of that graph are the strong components of the digraph. This algorithm is simple to describe and to implement, and its running time is dominated by the costs of the abstract–transitive-closure implementation, as described by, say, Property 19.10.
The algorithms that we consider in this section are triumphs of modern algorithm design that can find the strong components of any graph in linear time, a factor of V faster than the brute-force algorithm. For 100 vertices, these algorithms will be 100 times faster than the brute-force algorithm; for 1000 vertices, they will be 1000 times faster; and we can contemplate addressing problems involving billions of vertices. This problem is a prime example of the power of good algorithm design, one which has motivated many people to study graph algorithms closely. Where else might we contemplate reducing resource usage by a factor of 1 billion or more with an elegant solution to an important practical problem?
The history of this problem is instructive ( see reference section ). In the 1950s and 1960s, mathematicians and computer scientists began to study graph algorithms in earnest in a context where the analysis of algorithms itself was under development as a field of study. The broad variety of graph algorithms to be considered—coupled with ongoing developments in computer systems, languages, and our understanding of performing computations efficiently—left many difficult problems unsolved. As computer scientists began to understand many of the basic principles of the analysis of algorithms, they began to understand which graph problems could be solved efficiently and which could not and then to develop increasingly efficient algorithms for the former set of problems. Indeed, R. Tarjan introduced linear-time algorithms for strong connectivity and other graph problems in 1972, the same year that R. Karp documented the intractability of the traveling-salesperson problem and many other graph problems. Tarjan’s algorithm has been a staple of advanced courses in the analysis of algorithms for many years because it solves an important practical problem using simple data structures. In the 1980s, R. Kosaraju took a fresh look at the problem and developed a new solution; people later realized that a paper that describes essentially the same method appeared in the Russian scientific literature in 1972. Then, in 1999, H. Gabow found a simple implementation of one of the first approaches tried in the 1960s, giving a third linear-time algorithm for this problem.
The point of this story is not just that difficult graph-processing problems can have simple solutions, but also that the abstractions that we are using (DFS and adjacency lists) are more powerful than we might realize. As we become more accustomed to using these and similar tools, we should not be surprised to discover simple solutions to other important graph problems as well. Researchers still seek concise implementations like these for numerous other important graph algorithms; many such algorithms remain to be discovered.
Figure 19.28 Computing strong components (Kosaraju’s algorithm)
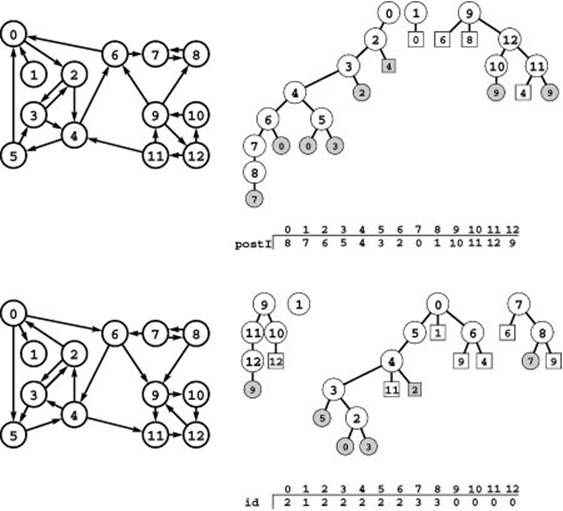
To compute the strong components of the digraph at the lower left, we first do a DFS of its reverse (top left), computing a postorder vector that gives the vertex indices in the order in which the recursive DFS completed (top). This order is equivalent to a postorder walk of the DFS forest (top right). Then we use the reverse of that order to do a DFS of the original digraph (bottom). First we check all nodes reachable from 9, then we scan from right to left through the vector to find that 1 is the rightmost unvisited vertex, so we do the recursive call for 1, and so forth. The trees in the DFS forest that results from this process define the strong components: All vertices in each tree have the same value in the vertex-indexed id vector (bottom).
Kosaraju’s method is simple to explain and implement. To find the strong components of a graph, first run DFS on its reverse, computing the permutation of vertices defined by the postorder numbering. (This process constitutes a topological sort if the digraph is a DAG.) Then, run DFS again on the graph, but to find the next vertex to search (when calling the recursive search function, both at the outset and each time that the recursive search function returns to the top-level search function), use the unvisited vertex with the highest postorder number.
The magic of the algorithm is that, when the unvisited vertices are checked according to the topological sort in this way, the trees in the DFS forest define the strong components just as trees in a DFS forest define the connected components in undirected graphs—two vertices are in the same strong component if and only if they belong
Program 19.10 Strong components (Kosaraju’s algorithm)
Clients can use objects of this class to find the number of strong components of a digraph (count) and to do strong-connectivity tests (stronglyconnected). The SC constructor first builds the reverse di-graph and does a DFS to compute a postorder numbering. Next, it does a DFS of the original digraph, using the reverse of the postorder from the first DFS in the search loop that calls the recursive function. Each recursive call in the second DFS visits all the vertices in a strong component.

to the same tree in this forest. Figure 19.28 illustrates this fact for our example, and we will prove it in a moment. Therefore, we can assign component numbers as we did for undirected graphs, incrementing the component number each time that the recursive function returns to the top-level search function. Program 19.10 is a full implementation of the method.
Property 19.14 Kosaraju’s method finds the strong components of a graph in linear time and space.
Proof: The method consists of minor modifications to two DFS procedures, so the running time is certainly proportional to V2 for dense graphs and V + E for sparse graphs (using an adjacency-lists representation), as usual. To prove that it computes the strong components properly, we have to prove that two vertices s and t are in the same tree in the DFS forest for the second search if and only if they are mutually reachable.
If s and t are mutually reachable, they certainly will be in the same DFS tree because when the first of the two is visited, the second is unvisited and is reachable from the first and so will be visited before the recursive call for the root terminates.
To prove the converse, we assume that s and t are in the same tree, and let r be the root of the tree. The fact that s is reachable from r (through a directed path of tree edges) implies that there is a directed path from s to r in the reverse digraph. Now, the key to the proof is that there must also be a path from r to s in the reverse digraph because r has a higher postorder number than s (since r was chosen first in the second DFS at a time when both were unvisited) and there is a path from s to r: If there were no path from r to s, then the path from s to r in the reverse would leave s with a higher postorder number. Therefore, there are directed paths from s to r and from r to s in the digraph and its reverse: s and r are strongly connected. The same argument proves that t and r are strongly connected, and therefore s and t are strongly connected.
The implementation for Kosaraju’s algorithm for the adjacency-matrix digraph representation is even simpler than Program 19.10 because we do not need to compute the reverse explicitly; that problem is left as an exercise (see Exercise 19.125).
Program 19.11 Strong components (Tarjan’s algorithm)
This DFS class is another implementation of the same interface as Program 19.10. It uses a stack S to hold each vertex until determining that all the vertices down to a certain point at the top of the stack belong to the same strong component. The vertex-indexed vector low keeps track of the lowest preorder number reachable via a series of down links followed by one up link from each node ( see text ).

Program 19.10 represents an optimal solution to the strong-connectivity problem that is analogous to our solutions for connectivity in Chapter 18. In Section 19.9, we examine the task of extending this solution to compute the transitive closure and to solve the reachability (abstract–transitive-closure) problem for digraphs.
First, however, we consider Tarjan’s algorithm and Gabow’s algorithm—ingenious methods that require only a few simple modifications to our basic DFS procedure. They are preferable to Kosaraju’s algorithm because they use only one pass through the graph and because they do not require computation of the reverse for sparse graphs.
Tarjan’s algorithm is similar to the program that we studied in Chapter 17 for finding bridges in undirected graphs (see Program 18.7). The method is based on two observations that we have already made in other contexts. First, we consider the vertices in reverse topological order so that when we reach the end of the recursive function for a vertex we know we will not encounter any more vertices in the same strong component (because all the vertices that can be reached from that vertex have been processed). Second, the back links in the tree provide a second path from one vertex to another and bind together the strong components.
The recursive DFS function uses the same computation as Program 18.7 to find the highest vertex reachable (via a back edge) from any descendant of each vertex. It also uses a vertex-indexed vector to keep track of the strong components and a stack to keep track of the current search path. It pushes the vertex names onto a stack on entry to the recursive function, then pops them and assigns component numbers after visiting the final member of each strong component. The algorithm is based on our ability to identify this moment with a simple test (based on keeping track of the highest ancestor reachable via one up link from all descendants of each node) at the end of the recursive procedure that tells us that all vertices encountered since entry (except those already assigned to a component) belong to the same strong component.
The implementation in Program 19.11 is a succinct and complete description of the algorithm that fills in the details missing from the brief sketch just given. Figure 19.29 illustrates the operation of the algorithm for our sample digraph from Figure 19.1.
Figure 19.29 Computing strong components (Tarjan and Gabow algorithms)

Tarjan’s algorithm is based on a recursive DFS, augmented to push vertices on a stack. It computes a component index for each vertex in a vertex-indexed vector id, using auxiliary vectors pre and low (center). The DFS tree for our sample graph is shown at the top and an edge trace at the bottom left. In the center at the bottom is the main stack: We push vertices reached by tree edges. Using a DFS to consider the vertices in reverse topological order, we compute, for each v, the highest point reachable via a back link from an ancestor (low[v]). When a vertex v has pre[v] = low[v] (vertices 11, 1, 0, and 7 here) we pop it and all the vertices above it (shaded) and assign them all the next component number.
In Gabow’s algorithm, we push vertices on the main stack, just as in Tarjan’s algorithm, but we also keep a second stack (bottom right) with vertices on the search path that are known to be in different strong components, by popping all vertices after the destination of each back edge. When we complete a vertex v with v at the top of this second stack (shaded), we know that all vertices above v on the main stack are in the same strong component.
Property 19.15 Tarjan’s algorithm finds the strong components of a digraph in linear time.
Proof sketch: If a vertex s has no descendants or up links in the DFS tree, or if it has a descendant in the DFS tree with an up link that points to s and no descendants with up links that point higher up in the tree, then it and all its descendants (except those vertices that satisfy the same property and their descendants) constitute a strong component. To establish this fact, we note that every descendant t of s that does not satisfy the stated property has some descendant that has an up link pointing higher than t in the tree. There is a path from s to t down through the tree and we can find a path from t to s as follows: Go down from t to the vertex with the up link that reaches past t, then continue the same process from that vertex until reaching s.
As usual, the method is linear time because it consists of adding a few constant-time operations to a standard DFS.
In 1999 Gabow discovered the version of Tarjan’s algorithm in Program 19.12. The algorithm maintains the same stack of vertices in the same way as does Tarjan’s algorithm, but it uses a second stack (instead of a vertex-indexed vector of preorder numbers) to decide when to pop all the vertices in each strong component from the main stack. The second stack contains vertices on the search path. When a back edge shows that a sequence of such vertices all belong to the same strong component, we pop that stack to leave only the destination vertex of the back edge, which is nearer the root of the tree than are any of the other vertices. After processing all the edges for each vertex (making recursive calls for the tree edges, popping the path stack for the back edges, and ignoring the down edges), we check to see whether the current vertex is at the top of the path stack. If it is, it and all the vertices above it on the main stack make a strong component, and we pop them and assign the next strong component number to them, as we did in Tarjan’s algorithm.
The example in Figure 19.29 also shows the contents of this second stack. Thus, this figure also illustrates the operation of Gabow’s algorithm.
Property 19.16 Gabow’s algorithm finds the strong components of a digraph in linear time.
Program 19.12 Strong components (Gabow’s algorithm)
This alternate implementation of the recursive member function in Program 19.11 uses a second stack path instead of the vertex-indexed vector low to decide when to pop the vertices in each strong component from the main stack ( see text ).

Formalizing the argument just outlined and proving the relationship between the stack contents that it depends upon is an instructive exercise for mathematically inclined readers (see Exercise 19.132). As usual, the method is linear time because it consists of adding a few constant-time operations to a standard DFS.
The strong-components algorithms that we have considered in this section are all ingenious and are deceptively simple. We have considered all three because they are testimony to the power of fundamental data structures and carefully crafted recursive programs. From a practical standpoint, the running time of all the algorithms is proportional to the number of edges in the digraph, and performance differences are likely to be dependent upon implementation details. For example, pushdown-stack ADT operations constitute the inner loop of Tarjan’s and Gabow’s algorithm. Our implementations use the bare-bones stack class implementations of Chapter 4; implementations that use STL stacks, which do error-checking and carry other overhead, may be slower. The implementation of Kosaraju’s algorithm is perhaps the simplest of the three, but it suffers the slight disadvantage (for sparse digraphs) of requiring three passes through the edges (one to make the reverse and two DFS passes).
Next, we consider a key application of computing strong components: building an efficient reachability (abstract–transitive-closure) ADT for digraphs.
Exercises
• 19.120 Describe what happens when you use Kosaraju’s algorithm to find the strong components of a DAG.
• 19.121 Describe what happens when you use Kosaraju’s algorithm to find the strong components of a digraph that consists of a single cycle.
•• 19.122 Can we avoid computing the reverse of the digraph in the adjacency-lists version of Kosaraju’s method (Program 19.10) by using one of the three techniques mentioned in Section 19.4 for avoiding the reverse computation when doing a topological sort? For each technique, give either a proof that it works or a counterexample that shows that it does not work.
• 19.123 Show, in the style of Figure 19.28, the DFS forests and the contents of the auxiliary vertex-indexed vectors that result when you use Kosaraju’s algorithm to compute the strong components of the reverse of the digraph in Figure 19.5. (You should have the same strong components.)
19.124 Show, in the style of Figure 19.28, the DFS forests and the contents of the auxiliary vertex-indexed vectors that result when you use Kosaraju’s algorithm to compute the strong components of the digraph
3-7 1-4 7-8 0-5 5-2 3-8 2-9 0-6 4-9 2-6 6-4.
• 19.125 Implement Kosaraju’s algorithm for finding the strong components of a digraph for a digraph representation that suports edge existence testing. Do not explicitly compute the reverse. Hint: Consider using two different recursive DFS functions.
• 19.126 Describe what happens when you use Tarjan’s algorithm to find the strong components of a DAG.
• 19.127 Describe what happens when you use Tarjan’s algorithm to find the strong components of a digraph that consists of a single cycle.
• 19.128 Show, in the style of Figure 19.29, the DFS forest, stack contents during the execution of the algorithm, and the final contents of the auxiliary vertex-indexed vectors that result when you use Tarjan’s algorithm to compute the strong components of the reverse of the digraph in Figure 19.5. (You should have the same strong components.)
19.129 Show, in the style of Figure 19.29, the DFS forest, stack contents during the execution of the algorithm, and the final contents of the auxiliary vertex-indexed vectors that result when you use Tarjan’s algorithm to compute the strong components of the digraph
3-7 1-4 7-8 0-5 5-2 3-8 2-9 0-6 4-9 2-6 6-4.
• 19.130 Modify the implementations of Tarjan’s algorithm in Program 19.11 and of Gabow’s algorithm in Program 19.12 such that they use sentinel values to avoid the need to check explicitly for cross links.
19.131 Show, in the style of Figure 19.29, the DFS forest, contents of both stacks during the execution of the algorithm, and the final contents of the auxiliary vertex-indexed vectors that result when you use Gabow’s algorithm to compute the strong components of the digraph
3-7 1-4 7-8 0-5 5-2 3-8 2-9 0-6 4-9 2-6 6-4.
• 19.132 Give a full proof of Property 19.16.
• 19.133 Develop a version of Gabow’s algorithm that finds bridges and edge-connected components in undirected graphs.
• 19.134 Develop a version of Gabow’s algorithm that finds articulation points and biconnected components in undirected graphs.
19.135 Develop a table in the spirit of Table 18.1 to study strong connectivity in random digraphs (see Table 19.2). Let S be the set of vertices in the largest strong component. Keep track of the size of S and study the percentages of edges in the following four classes: those connecting two vertices in S, those pointing out of S, those pointing in to S, those connecting two vertices not in S.
19.136 Run empirical tests to compare the brute-force method for computing strong components described at the beginning of this section, Kosaraju’s algorithm, Tarjan’s algorithm, and Gabow’s algorithm, for various types of digraphs (see Exercises 19.11–18).
••• 19.137 Develop a linear-time algorithm for strong 2-connectivity: Determine whether a strongly connected digraph has the property that it remains strongly connected after removing any vertex (and all its incident edges).
All materials on the site are licensed Creative Commons Attribution-Sharealike 3.0 Unported CC BY-SA 3.0 & GNU Free Documentation License (GFDL)
If you are the copyright holder of any material contained on our site and intend to remove it, please contact our site administrator for approval.
© 2016-2025 All site design rights belong to S.Y.A.