Algorithms Third Edition in C++ Part 5. Graph Algorithms (2006)
CHAPTER TWENTY-ONE
Shortest Paths
21.5 Euclidean Networks
In applications where networks model maps, our primary interest is often in finding the best route from one place to another. In this section, we examine a strategy for this problem: a fast algorithm for the source–sink shortest-path problem in Euclidean networks, which are networks whose vertices are points in the plane and whose edge weights are defined by the geometric distances between the points.
These networks satisfy two important properties that do not necessarily hold for general edge weights. First, the distances satisfy the triangle inequality: The distance from s to d is never greater than the distance from s to x plus the distance from x to d. Second, vertex positions give a lower bound on path length: No path from s to d will be shorter than the distance from s to d. The algorithm for the source–sink shortest-paths problem that we examine in this section takes advantage of these two properties to improve performance.
Often, Euclidean networks are also symmetric: Edges run in both directions. As mentioned at the beginning of the chapter, such networks arise immediately if, for example, we interpret the adjacency-matrix or adjacency-lists representation of an undirected weighted Euclidean graph (seeSection 20.7) as a weighted digraph (network). When we draw an undirected Euclidean network, we assume this interpretation to avoid proliferation of arrowheads in the drawings.
The basic idea is straightforward: Priority-first search provides us with a general mechanism to search for paths in graphs. With Dijkstra’s algorithm, we examine paths in order of their distance from the start vertex. This ordering ensures that, when we reach the sink, we have examined all paths in the graph that are shorter, none of which took us to the sink. But in a Euclidean graph, we have additional information: If we are looking for a path from a source s to a sink d and we encounter a third vertex v, then we know that not only do we have to take the path that we have found from s to v, but also the best that we could possibly do in traveling from v to d is first to take an edge v-w and then to find a path whose length is the straight-line distance from w to d (see Figure 21.18). With priority-first search, we can easily take into account this extra information to improve performance. We use the standard algorithm, but we use the sum of the following three quantities as the priority of each edge v-w: the length of the known path from s to v, the weight of the edge v-w, and the distance from w to t. If we always pick the edge for which this number is smallest, then, when we reach t, we are still assured that there is no shorter path in the graph from s to t. Furthermore, in typical networks we reach this conclusion after doing far less work than we would were we using Dijkstra’s algorithm.
Figure 21.18 Edge relaxation (Euclidean)
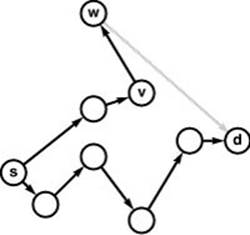
In a Euclidean graph, we can take distances to the destination into account in the relaxation operation as we compute shortest paths. In this example, we could deduce that the path depicted from s to v plus v-w cannot lead to a shorter path from s to d than the one already found because the length of any such path must be at least the length of the path from s to v plus the length of v-w plus the straight-line distance from w to d, which is greater than the length of the known path from s to d. Tests like this one can significantly reduce the number of paths that we have to consider.
To implement this approach, we use a standard PFS implementation of Dijkstra’s algorithm (Program 21.1, since Euclidean graphs are normally sparse, but also see Exercise 21.73) with two changes: First, instead of initializing wt[s] at the beginning of the search to 0.0, we set it to the quantity dist(s, d), where distance is a function that returns the distance between two vertices. Second, we define the priority P to be the function
(wt[v] + e->wt() + distance(w, d) - distance(v, d))
instead of the function (wt[v] + e->wt()) that we used in Program 21.1 (recall that v and w are local variables that are set to the values e->v() and e->w(), respectively. These changes, to which we refer as the Euclidean heuristic, maintain the invariant that the quantity wt[v] - distance(v, d) is the length of the shortest path through the network from s to v, for every tree vertex v (and therefore wt[v] is a lower bound on the length of the shortest possible path through v from s to d). We compute wt[w] by adding to this quantity the edge weight (the distance to w) plus the distance from w to the sink d.
Figure 21.19 Shortest path in a Euclidean graph

When we direct the shortest-path search towards the destination vertex, we can restrict the search to vertices within a relatively small ellipse around the path, as illustrated in these three examples, which show SPT subtrees from the examples in Figure 21.12.
Property 21.11 Priority-first search with the Euclidean heuristic solves the source–sink shortest-paths problem in Euclidean graphs.
Proof: The proof of Property 21.2 applies: At the time that we add a vertex x to the tree, the addition of the distance from x to d to the priority does not affect the reasoning that the tree path from s to x is a shortest path in the graph from s to x, since the same quantity is added to the length of all paths to x. When d is added to the tree, we know that no other path from s to d is shorter than the tree path, because any such path must consist of a tree path followed by an edge to some vertex w that is not on the tree, followed by a path from w to d (whose length cannot be shorter than the distance from w to d); and, by construction, we know that the length of the path from s to w plus the distance from w to d is no smaller than the length of the tree path from s to d.
In Section 21.6, we discuss another simple way to implement the Euclidean heuristic. First, we make a pass through the graph to change the weight of each edge: For each edge v-w, we add the quantity distance(w, d) - distance(v, d). Then, we run a standard shortest-path algorithm, starting at s (with wt[s] initialized to distance(s, d)) and stopping when we reach d. This method is computationally equivalent to the method that we have described (which essentially computes the same weights on the fly) and is a specific example of a basic operation known as reweighting a network. Reweighting plays an essential role in solving the shortest-paths problems with negative weights; we discuss it in detail in Section 21.6.
The Euclidean heuristic affects the performance but not the correctness of Dijkstra’s algorithm for the source–sink shortest-paths computation. As discussed in the proof of Property 21.2, using the standard algorithm to solve the source–sink problem amounts to building an SPT that has all vertices closer to the start than the sink d. With the Euclidean heuristic, the SPT contains just the vertices whose path from s plus distance to d is smaller than the length of the shortest path from s to d. We expect this tree to be substantially smaller for many applications because the heuristic prunes a substantial number of long paths. The precise savings is dependent on the structure of the graph and the geometry of the vertices. Figure 21.19 shows the operation of the Euclidean heuristic on our sample graph, where the savings are substantial. We refer to the method as a heuristic because there is no guarantee that there will be any savings at all: It could always be the case that the only path from source to sink is a long one that wanders arbitrarily far from the source before heading back to the sink (see Exercise 21.80).
Figure 21.20 Euclidean heuristic cost bounds
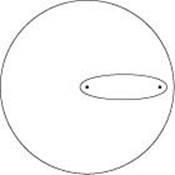
When we direct the shortest-path search towards the destination vertex, we can restrict the search to vertices within an ellipse around the path, as compared to the circle centered at s that is required by Dijkstra’s algorithm. The radius of the circle and the shape of the ellipse are determined by the length of the shortest path.
Figure 21.20 illustrates the basic underlying geometry that describes the intuition behind the Euclidean heuristic: If the shortest-path length from s to d is z, then vertices examined by the algorithm fall roughly within the ellipse defined as the locus of points x for which the distance from s to x plus the distance from x to d is equal to z. For typical Euclidean graphs, we expect the number of vertices in this ellipse to be far smaller than the number of vertices in the circle of radius z that is centered at the source (those that would be examined by Dijkstra’s algorithm).
Precise analysis of the savings is a difficult analytic problem and depends on models of both random point sets and random graphs (see reference section). For typical situations, we expect that, if the standard algorithm examines X vertices in computing a source–sink shortest path, the Euclidean heuristic will cut the cost to be proportional to ![]() , which leads to an expected running time proportional to
, which leads to an expected running time proportional to ![]() for dense graphs and proportional to pV for sparse graphs. This example illustrates that the difficulty of developing an appropriate model or analyzing associated algorithms should not dissuade us from taking advantage of the substantial savings that are available in many applications, particularly when the implementation (add a term to the priority) is trivial.
for dense graphs and proportional to pV for sparse graphs. This example illustrates that the difficulty of developing an appropriate model or analyzing associated algorithms should not dissuade us from taking advantage of the substantial savings that are available in many applications, particularly when the implementation (add a term to the priority) is trivial.
The proof of Property 21.11 applies for any function that gives a lower bound on the distance from each vertex to d. Might there be other functions that will cause the algorithm to examine even fewer vertices than the Euclidean heuristic? This question has been studied in a general setting that applies to a broad class of combinatorial search algorithms. Indeed, the Euclidean heuristic is a specific instance of an algorithm called A * (pronounced “ay-star”). This theory tells us that using the best available lower-bound function is optimal; stated another way, the better the bound function, the more efficient the search. In this case, the optimality of A* tells us that the Euclidean heuristic will certainly examine no more vertices than Dijkstra’s algorithm (which is A* with a lower bound of 0). The analytic results just described give more precise information for specific random network models.
We can also use properties of Euclidean networks to help build efficient implementations of the abstract–shortest-paths ADT, trading time for space more effectively than we can for general networks (see Exercises 21.48 through 21.50). Such algorithms are important in applications such as map processing, where networks are huge and sparse. For example, suppose that we want to develop a navigation system based on shortest paths for a map with millions of roads. We perhaps can store the map itself in a small onboard computer, but the distances and paths matrices are much too large to be stored (see Exercises 21.39 and 21.40); therefore, the all-paths algorithms of Section 21.3 are not effective. Dijkstra’s algorithm also may not give sufficiently short response times for huge maps. Exercises 21.77 through 21.78 explore strategies whereby we can invest a reasonable amount of preprocessing and space to provide fast responses to source– sink shortest-paths queries.
Exercises
• 21.68 Find a large Euclidean graph online—perhaps a map with an underlying table of locations and distances between them, telephone connections with costs, or airline routes and rates.
21.69 Using the strategies described in Exercises 17.71 through 17.73, write programs that generate random Euclidean graphs by connecting vertices arranged in a ![]() -by-
-by-![]() grid.
grid.
• 21.70 Show that the partial SPT computed by the Euclidean heuristic is independent of the value that we use to initialize wt[s]. Explain how to compute the shortest-path lengths from the initial value.
• 21.71 Show, in the style of Figure 21.10, what is the result when you use the Euclidean heuristic to compute a shortest path from 0 to 6 in the network defined in Exercise 21.1.
21.72 Describe what happens if the function distance(s, t), used for the Euclidean heuristic, returns the actual shortest-path length from s to t for all pairs of vertices.
21.73 Develop an class implementation for shortest paths in dense Euclidean graphs that is based upon a graph representation that supports the edge function and an implementation of Dijkstra’s algorithm (Program 20.6, with an appropriate priority function).
21.74 Run empirical studies to test the effectiveness of the Euclidean shortest-path heuristic, for various Euclidean networks (see Exercises 21.9, 21.68, 21.69, and 21.80). For each graph, generate V/ 10 random pairs of vertices, and print a table that shows the average distance between the vertices, the average length of the shortest path between the vertices, the average ratio of the number of vertices examined with the Euclidean heuristic to the number of vertices examined with Dijkstra’s algorithm, and the average ratio of the area of the ellipse associated with the Euclidean heuristic with the area of the circle associated with Dijkstra’s algorithm.
21.75 Develop a class implementation for the source-sink shortest-paths problemin Euclidean graphs that is based on the bidirectional search described in Exercise 21.35.
• 21.76 Use a geometric interpretation to provide an estimate of the ratio of the number of vertices in the SPT produced by Dijkstra’s algorithm for the source–sink problem to the number of vertices in the SPTs produced in the two-way version described in Exercise 21.75.
21.77 Develop a class implementation for shortest paths in Euclidean graphs that performs the following preprocessing step in the constructor: Divide the map region into a W -by-W grid, and then use Floyd’s all-pairs shortest-paths algorithm to compute a W2-by-W2 matrix, where row i and column j contain the length of a shortest path connecting any vertex in grid square i to any vertex in grid square j. Then, use these shortest-path lengths as lower bounds to improve the Euclidean heuristic. Experiment with a few different values of W such that you expect a small constant number of vertices per grid square.
21.78 Develop an implementation of the all-pairs shortest-paths ADT for Euclidean graphs that combines the ideas in Exercises 21.75 and 21.77.
21.79 Run empirical studies to compare the effectiveness of the heuristics described in Exercises 21.75 through 21.78, for various Euclidean networks (see Exercises 21.9, 21.68, 21.69, and 21.80).
21.80 Expand your empirical studies to include Euclidean graphs that are derived by removal of all vertices and edges from a circle of radius r in the center, for r =0.1, 0.2, 0.3, and 0.4. (These graphs provide a severe test of the Euclidean heuristic.)
21.81 Give a direct implementation of Floyd’s algorithm for an implementation of the network ADT for implicit Euclidean graphs defined by N points in the plane with edges that connect points within d of each other. Do not explicitly represent the graph; rather, given two vertices, compute their distance to determine whether an edge exists and, if one does, what its length is.
21.82 Develop an implementation for the scenario described in Exercise 21.81 that builds a neighbor graph and then uses Dijkstra’s algorithm from each vertex (see Program 21.1).
21.83 Run empirical studies to compare the time and space needed by the algorithms in Exercises 21.81 and 21.82, for d = 0.1, 0.2, 0.3, and 0.4.
• 21.84 Write a client program that does dynamic graphical animations of the Euclidean heuristic. Your program should produce images like Figure 21.19 (see Exercise 21.38). Test your program on various Euclidean networks (see Exercises 21.9, 21.68, 21.69, and 21.80).