Algorithms Third Edition in C++ Part 5. Graph Algorithms (2006)
CHAPTER TWENTY-TWO
Network Flow
22.6 Network Simplex Algorithm
The running time of the cycle-canceling algorithm is based on not just the number of negative-cost cycles that the algorithm uses to reduce the flow cost but also the time that the algorithm uses to find each of the cycles. In this section, we consider a basic approach that both dramatically decreases the cost of identifying negative cycles and admits methods for reducing the number of iterations. This implementation of the cycle-canceling algorithm is known as the network simplex algorithm. It is based on maintaining a tree data structure and reweighting costs such that negative cycles can be identified quickly.
To describe the network simplex algorithm, we begin by noting that, with respect to any flow, each network edge u-v is in one of three states (see Figure 22.43):
Figure 22.43 Edge classification
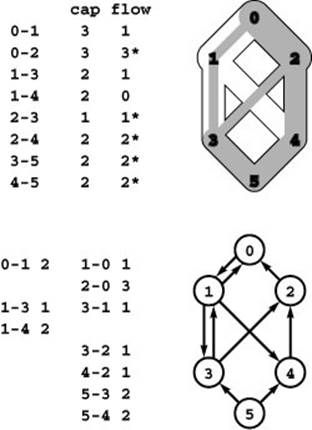
With respect to any flow, every edge is either empty, full, or partial (neither empty nor full). In this flow, edge 1-4 is empty; edges 0-2, 2-3, 2-4, 3-5, and 4-5 are full; and edges 0-1 and 1-3 are partial. Our conventions in figures give two ways to identify an edge’s state: In the flow column, 0 entries are empty edges; starred entries are full edges; and entries that are neither 0 nor starred are partial edges. In the residual network (bottom), empty edges appear only in the left column; full edges appear only in the right column; and partial edges appear in both columns.
• Empty, so flow can be pushed from only u to v
• Full, so flow can be pushed from only v to u
• Partial (neither empty nor full), so flow can pushed either way
This classification is familiar from our use of residual networks throughout this chapter. If u-v is an empty edge, then u-v is in the residual network, but v-u is not; if u-v is a full edge, then v-u is in the residual network, but u-v is not; if u-v is a partial edge, then both u-v and v-u are in the residual network.
Definition 22.10 Given a maxflow with no cycle of partial edges, a feasible spanning tree for the maxflow is any spanning tree of the network that contains all the flow’s partial edges.
In this context, we ignore edge directions in the spanning tree. That is, any set of V − 1 directed edges that connects the network’s V vertices (ignoring edge directions) constitutes a spanning tree, and a spanning tree is feasible if all nontree edges are either full or empty.
The first step in the network simplex algorithm is to build a spanning tree. One way to build it is to compute a maxflow, to break
Figure 22.44 Maxflow spanning tree
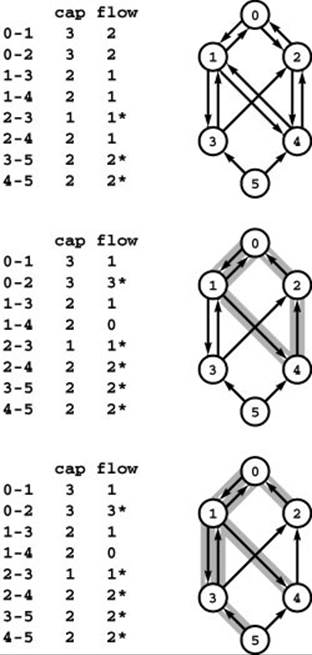
Given any maxflow (top), we can construct a maxflow that has a spanning tree such that no nontree edges are partial by the two-step process illustrated in this example. First, we break cycles of partial edges; in this case, we break the cycle 0-2-4-1-0 by pushing 1 unit of flow along it. We can always fill or empty at least one edge in this way; in this case, we empty 1-4 and fill both 0-2 and 2-4 (center). Second, we add empty or full edges to the set of partial edges to make a spanning tree; in this case, we add 0-2, 1-4 and 3-5 (bottom).
cycles of partial edges by augmenting along each cycle to fill or empty one of its edges, then to add full or empty edges to the remaining partial edges to make a spanning tree. An example of this process is illustrated in Program 22.44. Another option is to start with the maxflow in a dummy edge from source to sink. Then, this edge is the only possible partial edge, and we can build a spanning tree for the flow with any graph search. An example of such a spanning tree is illustrated in Program 22.45.
Now, adding any nontree edge to a spanning tree creates a cycle. The basic mechanism behind the network simplex algorithm is a set of vertex weights that allows immediate identification of the edges that, when added to the tree, create negative-cost cycles in the residual network. We refer to these vertex weights as potentials and use the notation ϕ (v) to refer to the potential associated with v. Depending on context, we refer to potentials as a function defined on the vertices, or as a set of integer weights with the implicit assumption that one is assigned to each vertex, or as a vertex-indexed vector (since we always store them that way in implementations).
Definition 22.11 Given a flow in a flow network with edge costs, let c (u, v)denote the cost of u-v in the flow’s residual network. For any potential function ϕ, the reduced cost of an edge u-v in the residual network with respect to ϕ, which we denote by c (u, v), is defined to be the value c(u, v)−(ϕ(u)− ϕ(v)).
In other words, the reduced cost of every edge is the difference between that edge’s actual cost and the difference of the potentials of the edge’s vertices. In the merchandise distribution application, we can see the intuition behind node potentials: If we interpret the potential ϕ (u) as the cost of buying a unit of material at node u, the full cost c (u, v)+ ϕ(u)− ϕ (v) is the cost of buying at u, shipping to v and selling at v.
We maintain a vertex-indexed vector phi for the vertex potentials and compute the reduced cost of an edge v-w by subtracting from the edge’s cost the value (phi[v] - phi[w]). That is, there is no need to store the reduced edge costs anywhere, because it is so easy to compute them.
In the network simplex algorithm, we use feasible spanning trees to define vertex potentials such that reduced edge costs with respect to those potentials give direct information about negative-cost cycles.
Figure 22.45 Spanning tree for dummy maxflow
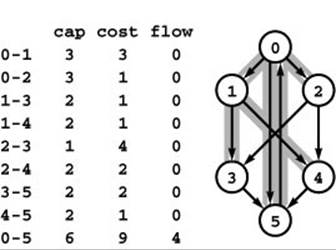
If we start with flow on a dummy edge from source to sink, then that is the only possible partial edge, so we can use any spanning tree of the remaining nodes to build a spanning tree for the flow. In the example, the edges 0-5, 0-1, 0-2, 1-3, and 1-4 comprise a spanning tree for the initial maxflow. All of the nontree edges are empty.
Specifically, we maintain a feasible spanning tree throughout the execution of the algorithm, and we set the values of the vertex potentials such that all tree edges have reduced cost zero.
Property 22.25 We say that a set of vertex potentials is valid with respect to a spanning tree if all tree edges have zero reduced cost. All valid vertex potentials for any given spanning tree imply the same reduced costs for each network edge.
Proof: Given two different potential functions ϕ and ϕ ′ that are both valid with respect to a given spanning tree, we show that they differ by an additive constant: That ϕ (u) =ϕ ′(u)+ ′for all u and some constant. Then, ϕ (u)−ϕ(v) =ϕ ′(u)−ϕ′(v) for all u and v, implying that all reduced costs are the same for the two potential functions.
For any two vertices u and v that are connected by a tree edge, we must have ϕ (v) =ϕ (u)c (u, v), by the following argument. If u-v is a tree edge, then ϕ (v) must − be equal to ϕ (u)c (u, v) to make the reduced cost c (u, v)− ϕ (u)+ ϕ (v) equal to zero; if v-u is a tree edge, then ϕ (v) must be equal to ϕ (u)+ c (v, u) =ϕ (u)c (u, v) to make the reduced cost c (v, u)− ϕ (v)+ ϕ (u) equal to zero. The same argument holds for ϕ ′, so we must also have ϕ ′(v) =ϕ ′(u)c (u, v).
Subtracting, we find that ϕ (v)− ϕ ′(v) =ϕ −(u)ϕ ′(u) for any u and v connected by a tree edge. Denoting this difference by′ for any vertex and applying the equality along the edges of any search tree of the spanning tree immediately gives the desired result that ϕ(u) =ϕ ′(u)+ ′for all u.
Another way to imagine the process of defining a set of valid vertex potentials is that we start by fixing one value, then compute the values for all vertices connected to that vertex by tree edges, then compute them for all vertices connected to those vertices, and so forth. No matter where we start the process, the potential difference between any two vertices is the same, determined by the structure of the tree. Program 22.46 depicts an example. We consider the details of the task of computing potentials after we examine the relationship between reduced costs on nontree edges and negative-cost cycles.
Property 22.26 We say that a nontree edge is eligible if the cycle that it creates with tree edges is a negative-cost cycle in the residual network. An edge is eligible if and only if it is a full edge with positive reduced cost or an empty edge with negative reduced cost.
Figure 22.46 Vertex potentials
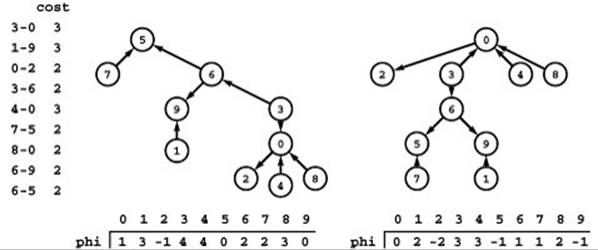
Vertex potentials are determined by the structure of the spanning tree and by an initial assignment of a potential value to any vertex. At left is a set of edges that comprise a spanning tree of the ten vertices 0 through 9. In the center is a representation of that tree with 5 at the root, vertices connected to 5 one level lower, and so forth. When we assign the root the potential value 0, there is a unique assignment of potentials to the other nodes that make the difference between the potentials of each edge’s vertices equal to its cost. At right is a different representation of the same tree with 0 at the root. The potentials that we get by assigning 0 the value 0 differ from those in the center by a constant offset. All our computations use the difference between two potentials: This difference is the same for any pair of potentials no matter what vertex we start with (and no matter what value we assign it), so our choice of starting vertex and value is immaterial.
Proof: Suppose that the edge u-v creates the cycle t1-t2-t3-…-td-t1 with tree edges t1-t2, t2-t3, …, where v is t1 and u is td. The reduced cost definitions of each edge imply the following:
c(u, v) = c (u, v)+ ϕ (u)− ϕ (t1)
c(t1,t2) =ϕ (t1)− ϕ (t2)
c(t2,t3) =ϕ (t2)ϕ (t3)
.
.
.
c(td−1,u)= ϕ(td−1)− ϕ(u)
The left-hand side of the sum of these equations gives the total cost of the cycle, and the right-hand side collapses to c (u, v). In other words, the edge’s reduced cost gives the cycle cost, so only the edges described can give a negative-cost cycle
Property 22.27 If we have a flow and a feasible spanning tree with no eligible edges, the flow is a mincost flow.
Proof: If there are no eligible edges, then there are no negative-cost cycles in the residual network, so the optimality condition of Property 22.23 implies that the flow is a mincost flow.
An equivalent statement is that if we have a flow and a set of vertex potentials such that reduced costs of tree edges are all zero, full nontree edges are all nonnegative, and empty nontree edges are all nonpositive, then the flow is a mincost flow.
If we have eligible edges, we can choose one and augment along the cycle that it creates with tree edges to get a lower-cost flow. As we did with the cycle-canceling implementation in Section 22.5, we go through the cycle to find the maximum amount of flow that we can push, then go through the cycle again to push that amount, which fills or empties at least one edge. If that is the eligible edge that we used to create the cycle, it becomes ineligible (its reduced cost stays the same, but it switches from full to empty or empty to full). Otherwise, it becomes partial. By adding it to the tree and removing a full edge or an empty edge from the cycle, we maintain the invariant that no nontree edges are partial and that the tree is a feasible spanning tree. Again, we consider the mechanics of this computation later in this section.
In summary, feasible spanning trees give us vertex potentials, which give us reduced costs, which give us eligible edges, which give us negative-cost cycles. Augmenting along a negative-cost cycle reduces the flow cost and also implies changes in the tree structure. Changes in the tree structure imply changes in the vertex potentials; changes in the vertex potentials imply changes in reduced edge costs; and changes in reduced costs imply changes in the set of eligible edges. After making all these changes, we can pick another eligible edge and start the process again. This generic implementation of the cycle-canceling algorithm for solving the mincost-flow problem is called the network simplex algorithm.
Build a feasible spanning tree and maintain vertex potentials such that all tree vertices have zero reduced cost. Add an eligible edge to the tree, augment the flow along the cycle that it makes with tree edges, and remove from the tree an edge that is filled or emptied, continuing until no eligible edges remain.
This implementation is a generic one because the initial choice of spanning tree, the method of maintaining vertex potentials, and the method of choosing eligible edges are not specified. The strategy for choosing eligible edges determines the number of iterations, which trades off against the differing costs of implementing various strategies and recalculating the vertex potentials.
Property 22.28 If the generic network simplex algorithm terminates, it computes a mincost flow.
Proof: If the algorithm terminates, it does so because there are no negative-cost cycles in the residual network, so by Property 22.23 the maxflow is of mincost.
The condition that the algorithm might not terminate derives from the possibility that augmenting along a cycle might fill or empty multiple edges, thus leaving edges in the tree through which no flow can be pushed. If we cannot push flow, we cannot reduce the cost, and we could get caught in an infinite loop adding and removing edges to make a fixed sequence of spanning trees. Several ways to avoid this problem have been devised; we discuss them later in this section after we look in more detail at implementations.
The first choice that we face in developing an implementation of the network simplex algorithm is what representation to use for the spanning tree. We have three primary computational tasks that involve the tree:
• Computing the vertex potentials
• Augmenting along the cycle (and identifying an empty or a full edge on it)
• Inserting a new edge and removing an edge on the cycle formed Each of these tasks is an interesting exercise in data structure and algorithm design. There are several data structures and numerous algorithms that we might consider, with varied performance characteristics. We begin by considering perhaps the simplest available data structure—which we first encountered in Chapter 1(!)—the parent-link tree representation. After we examine algorithms and implementations that are based on the parent-link representation for the tasks just listed and describe their use in the context of the network simplex algorithm, we discuss alternative data structures and algorithms.
As we did in several other implementations in this chapter, beginning with the augmenting-path maxflow implementation, we keep links into the network representation, rather than simple indices in the tree representation, to allow us to have access to the flow values that need to be changed without losing access to the vertex name.
Program 22.10 is an implementation that assigns vertex potentials in time proportional to V. It is based on the following idea, also illustrated in Program 22.47. We start with any vertex and recursively compute the potentials of its ancestors, following parent links up to the root, to which, by convention, we assign potential 0. Then, we
Program 22.10 Vertex potential calculation
The recursive function phiR follows parent links up the tree until finding one whose potential is valid (by convention the potential of the root is always valid), then computes potentials for vertices on the path on the way back down as the last actions of the recursive invocations. It marks each vertex whose potential it computes by setting its mark entry to the current value of valid.
int phiR(int v)
{
if (mark[v] == valid) return phi[v];
phi[v] = phiR(ST(v)) - st[v]->costRto(v);
mark[v] = valid;
return phi[v];
}
pick another vertex and use parent links to compute recursively the potentials of its ancestors. The recursion terminates when we reach an ancestor whose potential is known; then, on the way out of the recursion, we travel back down the path, computing each node’s potential from its parent. We continue this process until we have computed all potential values. Once we have traveled along a path, we do not revisit any of its edges, so this process runs in time proportional to V.
Given two nodes in a tree, their least common ancestor (LCA) is the root of the smallest subtree that contains them both. The cycle that we form by adding an edge connecting two nodes consists of that edge plus the edges on the two paths from the two nodes to their LCA. The augmenting cycle formed by adding v-w goes through v-w to w, up the tree to the LCA of v and w (say r), then down the tree to v, so we have to consider edges in opposite orientation in the two paths.
As before, we augment along the cycle by traversing the paths once to find the maximum amount of flow that we can push through their edges then traversing the two paths again, pushing flow through them. We do not need to consider edges in order around the cycle; it suffices to consider them all (in either direction). Accordingly, we can simply follow paths from each of the two nodes to their LCA. To augment along the cycle formed by the addition of v-w, we push flow from v to w; from v along the path to the LCA r; and from w along
Figure 22.47 Computing potentials through parent links
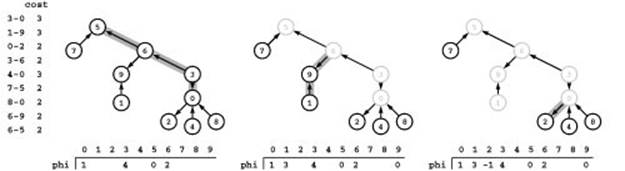
We start at 0, follow the path to the root, set pt[5] to 0, then work down the path, first setting 6 to make pt[6] - pt[5] equal to the cost of 6-5, then setting p[3] to make p[3] - p[6] equal to the cost of 3-6, and so forth (left). Then we start at 1 and follow parent links until hitting a vertex whose potential is known (6 in this case) and work down the path to compute potentials on 9 and 1 (center). When we start at 2, we can compute its potential from its parent (right); when we start at 3, we see that its potential is already known, and so forth. In this example, when we try each vertex after 1, we either find that its potential is already done or we can compute the value from its parent. We never retrace an edge, no matter what the tree structure, so the total running time is linear.
the path to r, but in reverse direction for each edge. Program 22.11 is an implementation of this idea, in the form of a function that augments a cycle and also returns an edge that is emptied or filled by the augmentation.
The implementation in Program 22.11 uses a simple technique to avoid paying the cost of initializing all the marks each time that we call it. We maintain the marks as global variables, initialized to zero. Each time that we seek an LCA, we increment a global counter and mark vertices by setting their corresponding entry in a vertex-indexed vector to that counter. After initialization, this technique allows us to perform the computation in time proportional to the length of the cycle. In typical problems, we might augment along a large number of small cycles, so the time saved can be substantial. As we learn, the same technique is useful in saving time in other parts of the implementation.
Our third tree-manipulation task is to substitute an edge u-v for another edge in the cycle that it creates with tree edges. Program 22.12 is an implementation of a function that accomplishes this task for the parent-link representation. Again, the LCA of u and v is important, because the edge to be removed is either on the path from u to the LCA or on the path from v to the LCA. Removing an edge detaches all its descendants from the tree, but we can repair the damage by reversing the links between u-v and the removed edge, as illustrated in Program 22.48.
These three implementations support the basic operations underlying the network simplex algorithm: We can choose an eligible edge by examining reduced costs and flows; we can use the parent-link representation of the spanning tree to augment along the negative cycle
Program 22.11 Augmenting along a cycle
To find the least common ancestor of two vertices, we mark nodes while moving up the tree from them in synchrony. The LCA is the root if it is the only marked node seen; otherwise the LCA is the first marked node seen that is not the root. To augment, we use a function similar to the one in Program 22.3 that preserves tree paths in st and returns an edge that was emptied or filled by the augmentation (see text).

Figure 22.48 Spanning tree substitution
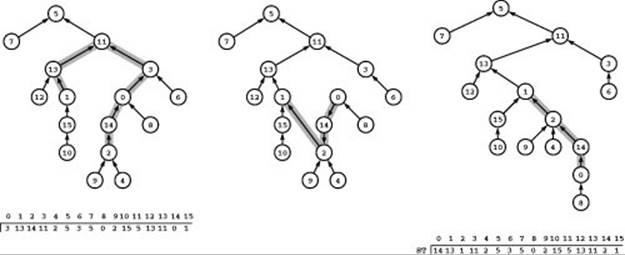
This example illustrates the basic tree-manipulation operation in the network simplex algorithm for the parent-link representation. At left is a sample tree with links all pointing upwards, as indicated by the parent-link structure ST. (In our code, the function ST computes the parent of the given vertex from the edge pointer in the vertex-indexed vector st.) Adding the edge 1-2 creates a cycle with the paths from 1 and 2 to their LCA, 11. If we then delete one of those edges, say 0-3, the structure remains a tree. To update the parent-link array to reflect the change, we switch the directions of all the links from 2 up to 3 (center). The tree at right is the same tree with node positions changed so that links all point up, as indicated by the parent-link array that represents the tree (bottom right).
formed with tree edges and the chosen eligible edge; and we can update the tree and recalculate potentials. These operations are illustrated for an example flow network in Figures 22.49 and 22.50.
Figure 22.49 illustrates initialization of the data structures using a dummy edge with the maxflow on it, as in Figure 22.42. Shown there are an initial feasible spanning tree with its parent-link representation, the corresponding vertex potentials, the reduced costs for the nontree edges, and the initial set of eligible edges. Also, rather than computing the maxflow value in the implementation, we use the outflow from the source, which is guaranteed to be no less than the maxflow value; we use the maxflow value here to make the operation of the algorithm easier to trace.
Figure 22.50 illustrates the changes in the data structures for each of a sequence of eligible edges and augmentations around negative-cost cycles. The sequence does not reflect any particular method for choosing eligible edges; it represents the choices that make the augmenting paths the same as depicted in Program 22.42. These figures show all vertex potentials and all reduced costs after each cycle augmentation, even though many of these numbers are implicitly defined and are not necessarily computed explicitly by typical implementations. The purpose of these two figures is to illustrate the overall progress of the algorithm and the state of the data structures as the algorithm moves
Program 22.12 Spanning tree substitution
The function update adds an edge to the spanning tree and removes an edge on the cycle thus created. The edge to be removed is on the path from one of the two vertices on the edge added to their LCA. This implementation uses the function onpath to find the edge removed and the function reverse to reverse the edges on the path between it and the edge added.

from one feasible spanning tree to another simply by adding an eligible edge and removing a tree edge on the cycle that is formed.
One critical fact that is illustrated in the example in Program 22.50 is that the algorithm might not even terminate, because full or empty edges on the spanning tree can stop us from pushing flow along the negative cycle that we identify. That is, we can identify an eligible edge and the negative cycle that it makes with spanning tree edges, but the maximum amount of flow that we can push along the cycle may be 0. In this case, we still substitute the eligible edge for an edge on the
Figure 22.49 Network simplex initialization
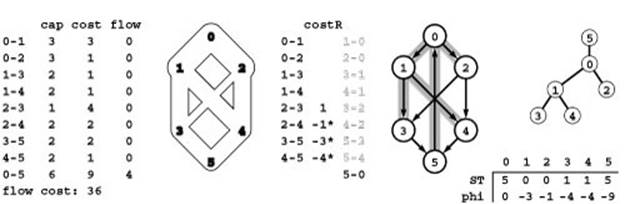
To initialize the data structures for the network simplex algorithm, we start with zero flow on all edges (left), then add a dummy edge 0-5 from source to sink with flow no less than the maxflow value (for clarity, we use a value equal to the maxflow value here). The cost value 9 for the dummy edge is greater than the cost of any cycle in the network; in the implementation, we use the value CV. The dummy edge is not shown in the flow network, but it is included in the residual network (center).
We initialize the spanning tree with the sink at the root, the source as its only child, and a search tree of the graph induced by the remaining nodes in the residual network. The implementation uses the parent-edge representation of the tree in the array st and the related parent-vertex function ST; our figures depict this representation and two others: the rooted representation shown on the right and the set of shaded edges in the residual network.
The vertex potentials are in the pt array and are computed from the tree structure so as to make the difference of a tree edge’s vertex potentials equal to its cost.
The column labeled costR in the center gives the reduced costs for nontree edges, which are computed for each edge by adding the difference of its vertex potentials to its cost. Reduced costs for tree edges are zero and left blank. Empty edges with negative reduced cost and full edges with positive reduced cost (eligible edges) are marked with asterisks.
cycle, but we make no progress in reducing the cost of the flow. To ensure that the algorithm terminates we need to prove that we cannot end up in an endless sequence of zero-flow augmentations.
If there is more than one full or empty edge on the augmenting cycle, the substitution algorithm in Program 22.12 always deletes from the tree the one closest to the LCA of the eligible edge’s two vertices. Fortunately, it has been shown that this particular strategy for choosing the edge to remove from the cycle suffices to ensure that the algorithm terminates (see reference section).
The final important choice that we face in developing an implementation of the network simplex algorithm is a strategy for identifying eligible edges and choosing one to add to the tree. Should we maintain a data structure containing eligible edges? If so, how sophisticated a data structure is appropriate? The answer to these questions depends somewhat on the application and the dynamics of solving particular instances of the problem. If the total number of eligible edges is small, then it is worthwhile to maintain a separate data structure; if most edges are eligible most of the time, it is not. Maintaining a separate data structure could spare us the expense of searching for eligible edges, but also could require costly update computations. What criteria should we use to pick from among the eligible edges? Again, there are many that we might adopt. We consider examples in our implementations, then discuss alternatives. For example, Program 22.13 illustrates a function that finds an eligible edge of minimal reduced cost: No other edge gives a cycle for which augmenting along the cycle would lead to a greater reduction in the total cost.
Program 22.14 is a full implementation of the network simplex algorithm that uses the strategy of choosing the eligible edge giving a negative cycle whose cost is highest in absolute value. The implementation
Figure 22.50 Residual networks and spanning trees (network simplex)
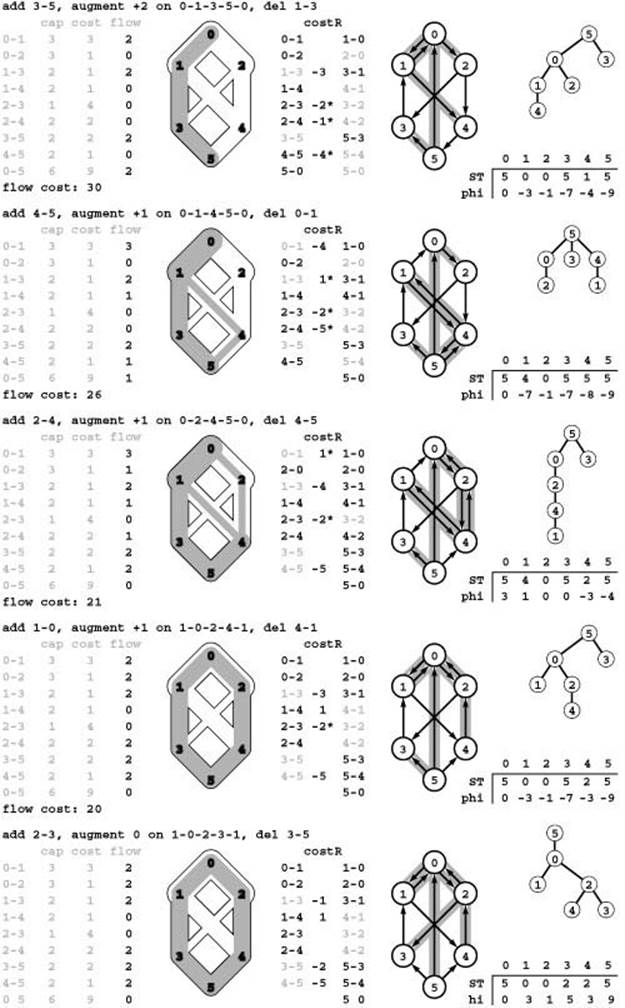
Each row in this figure corresponds to an iteration of the network simplex algorithm following the initialization depicted in Program 22.49: On each iteration, it chooses an eligible edge, augments along a cycle, and updates the data structures as follows: First, the flow is augmented, including implied changes in the residual network. Second, the tree structure ST is changed by adding an eligible edge and deleting an edge on the cycle that it makes with tree edges. Third, the table of potentials phi is updated to reflect the changes in the tree structure. Fourth, the reduced costs of the nontree edges (column marked costR in the center) are updated to reflect the potential changes, and these values used to identify empty edges with negative reduced cost and full edges with positive reduced costs as eligible edges (marked with asterisks on reduced costs). Implementations need not actually make all these computations (they only need to compute potential changes and reduced costs sufficient to identify an eligible edge), but we include all the numbers here to provide a full illustration of the algorithm.
The final augmentation for this example is degenerate. It does not increase the flow, but it leaves no eligible edges, which guarantees that the flow is a mincost maxflow.
Program 22.13 Eligible edge search
This function finds the eligible edge of lowest reduced cost. It is a straightforward implementation that that traverses all the edges in the network.

uses the tree-manipulation functions and the eligible-edge search of Programs 22.10 through 22.13, but the comments that we made regarding our first cycle-canceling implementation (Program 22.9) apply: It is remarkable that such a simple piece of code is sufficiently powerful to provide useful solutions in the context of a general problem-solving model with the reach of the mincost-flow problem.
The worst-case performance bound for Program 22.14 is at least a factor of V lower than that for the cycle-canceling implementation in Program 22.9, because the time per iteration is just E (to find the eligible edge) rather than V E (to find a negative cycle). Although we might suspect that using the maximum augmentation will result in fewer augmentations than just taking the first negative cycle provided by the Bellman–Ford algorithm, that suspicion has not been proved valid. Specific bounds on the number of augmenting cycles used are difficult to develop, and, as usual, these bounds are far higher than the numbers that we see in practice. As mentioned earlier, there are
Program 22.14 Network simplex (basic implementation)
This class uses the network simplex algorithm to solve the mincost flow problem. It uses a standard DFS function dfsR an initial tree (see Exercise 22.117), then it enters a loop where it uses the functions in Programs 22.10 through 22.13 to compute all the vertex potentials, examine all the edges to find the one that creates the lowest-cost negative cycle, and augment along that cycle.

theoretical results demonstrating that certain strategies can guarantee that the number of augmenting cycles is bounded by a polynomial in the number of edges, but practical implementations typically admit an exponential worst case.
In light of these considerations, there are many options to consider in pursuit of improved performance. For example, Program 22.15 is another implementation of the network simplex algorithm. The straightforward implementation in Program 22.14 always takes time proportional to V to revalidate the tree potentials and always takes time proportional to E to find the eligible edge with the largest reduced cost. The implementation in Program 22.15 is designed to eliminate both of these costs in typical networks.
First, even if choosing the maximum edge leads to the fewest number of iterations, expending the effort of examining every edge to find the maximum edge may not be worthwhile. We could do numerous augmentations along short cycles in the time that it takes to scan all the edges. Accordingly, it is worthwhile to consider the strategy of using any eligible edge, rather than taking the time to find a particular one. In the worst case, we might have to examine all the edges or a substantial fraction of them to find an eligible edge, but we typically expect to need to examine relatively few edges to find an eligible one. One approach is to start from the beginning each time; another is to pick a random starting point (see Exercise 22.126). This use of randomness also makes an artificially long sequence of augmenting paths unlikely.
Second, we adopt a lazy approach to computing potentials. Rather than compute all the potentials in the vertex-indexed vector phi, then refer to them when we need them, we call the function phiR to get each potential value; it travels up the tree to find a valid potential, then computes the necessary potentials on that path. To implement this approach, we simply change the function that defines the cost to use the function call phiR(u), instead of the array access phi[u]. In the worst case, we calculate all the potentials in the same way as before; but if we examine only a few eligible edges, then we calculate only those potentials that we need to identify them.
Such changes do not affect the worst-case performance of the algorithm, but they certainly speed it up in practical applications. Several other ideas for improving the performance of the network
Program 22.15 Network simplex (improved implementation)
Replacing references to phi by calls to phiR in the function R and replacing the for loop in the constructor in Program 22.14 by this code gives a network simplex implementation that saves time on each iteration by calculating potentials only when needed, and by taking the first eligible edge that it finds.
int old = 0;
for (valid = 1; valid != old; )
{
old = valid;
for (int v = 0; v < G.V(); v++)
{
typename Graph::adjIterator A(G, v);
for (Edge* e = A.beg(); !A.end(); e = A.nxt())
if (e->capRto(e->other(v)) > 0)
if (e->capRto(v) == 0)
{ update(augment(e), e); valid++; }
}
}
simplex algorithm are explored in the exercises (see Exercises 22.126 through 22.130); those represent only a small sample of the ones that have been proposed.
As we have emphasized throughout this book, the task of analyzing and comparing graph algorithms is complex. With the network simplex algorithm, the task is further complicated by the variety of different implementation approaches and the broad array of types of applications that we might encounter (see Section 22.5). Which implementation is best? Should we compare implementations based on the worst-case performance bounds that we can prove? How accurately can we quantify performance differences of various implementations, for specific applications. Should we use multiple implementations, each tailored to specific applications?
Readers are encouraged to gain computational experience with various network simplex implementations and to address some of these questions by running empirical studies of the kind that we have emphasized throughout this book. When seeking to solve mincost flow problems, we are faced with the familiar fundamental challenges, but the experience that we have gained in tackling increasingly difficult problems throughout this book provides ample background to develop efficient implementations that can effectively solve a broad variety of important practical problems. Some such studies are described in the exercises at the end of this and the next section, but these exercises should be viewed as a starting point. Each reader can craft a new empirical study that sheds light on some particular implementation/application pair of interest.
The potential to improve performance dramatically for critical applications through proper deployment of classic data structures and algorithms (or development of new ones) for basic tasks makes the study of network-simplex implementations a fruitful research area, and there is a large literature on network simplex implementations. In the past, progress in this research has been crucial, because it helps reduce the huge cost of solving network simplex problems. People tend to rely on carefully crafted libraries to attack these problems, and that is still appropriate in many situations. However, it is difficult for such libraries to keep up with recent research and to adapt to the variety of problems that arise in new applications. With the speed and size of modern computers, accessible implementations like Programs 22.12 and 22.13 can be starting points for the development of effective problem-solving tools for numerous applications.
Exercises
• 22.116 Give a maxflow with associated feasible spanning tree for the flow network shown in Program 22.10.
• 22.117 Implement the dfsR function for Program 22.14.
• 22.118 Implement a function that removes cycles of partial edges from a given network’s flow and builds a feasible spanning tree for the resulting flow, as illustrated in Program 22.44. Package your function so that it could be used to build the initial tree in Program 22.14 or Program 22.15.
22.119 In the example in Program 22.46, show the effect of reversing the direction of the edge connecting 6 and 5 on the potential tables.
• 22.120 Construct a flow network and exhibit a sequence of augmenting edges such that the generic network simplex algorithm does not terminate.
• 22.121 Show, in the style of Program 22.47, the process of computing potentials for the tree rooted at 0 in Program 22.46.
22.122 Show, in the style of Program 22.50, the process of computing a min-cost maxflow in the flow network shown in Program 22.10, starting with the basic maxflow and associated basic spanning tree that you found in Exercise 22.116.
• 22.123 Suppose that all nontree edges are empty. Write a function that computes the flows in the tree edges, putting the flow in the edge connecting v and its parent in the tree in the vth entry of a vector flow.
• 22.124 Do Exercise 22.123 for the case where some nontree edges may be full.
22.125 Use Program 22.12 as the basis for an MST algorithm. Run empirical tests comparing your implementation with the three basic MST algorithms described in Chapter 20 (see Exercise 20.66).
22.126 Describe how to modify Program 22.15 such that it starts the scan for an eligible edge at a random edge rather than at the beginning each time.
22.127 Modify your solution to Exercise 22.126 such that each time it searches for an eligible edge it starts where it left off in the previous search.
22.128 Modify the private member functions in this section to maintain a triply linked tree structure that includes each node’s parent, leftmost child, and right sibling (see Section 5.4). Your functions to augment along a cycle and substitute an eligible edge for a tree edge should take time proportional to the length of the augmenting cycle, and your function to compute potentials should take time proportional to the size of the smaller of the two subtrees created when the tree edge is deleted.
• 22.129 Modify the private member functions in this section to maintain, in addition to basic parent-edge tree vector, two other vertex-indexed vectors: one containing each vertex’s distance to the root, the other containing each vertex’s successor in a DFS. Your functions to augment along a cycle and substitute an eligible edge for a tree edge should take time proportional to the length of the augmenting cycle, and your function to compute potentials should take time proportional to the size of the smaller of the two subtrees created when the tree edge is deleted.
• 22.130 Explore the idea of maintaining a generalized queue of eligible edges. Consider various generalized-queue implementations and various improvements to avoid excessive edge-cost calculations, such as restricting attention to a subset of the eligible edges so as to limit the size of the queue or possibly allowing some ineligible edges to remain on the queue.
• 22.131 Run empirical studies to determine the number of iterations, the number of vertex potentials calculated, and the ratio of the running time to E for several versions of the network simplex algorithm, for various networks (see Exercises 22.7–12). Consider various algorithms described in the text and in the previous exercises, and concentrate on those that perform the best on huge sparse networks.
• 22.132 Write a client program that does dynamic graphical animations of network simplex algorithms. Your program should produce images like those in Program 22.50 and the other figures in this section (see Exercise 22.48). Test your implementation for the Euclidean networks amongExercises 22.7–12.
Figure 22.51 Reduction from shortest paths
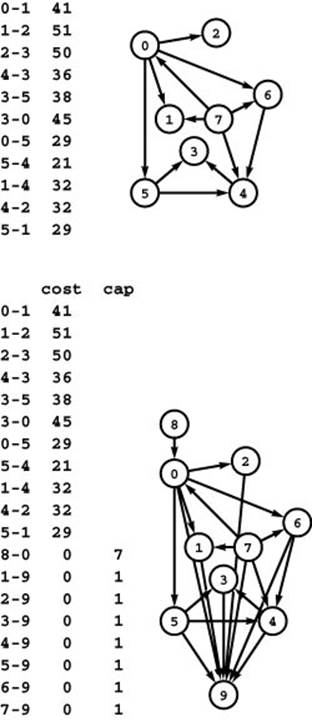
Finding a single-source–shortest-paths tree in the network at the top is equivalent to solving the mincost-maxflow problem in the flow network at the bottom.
All materials on the site are licensed Creative Commons Attribution-Sharealike 3.0 Unported CC BY-SA 3.0 & GNU Free Documentation License (GFDL)
If you are the copyright holder of any material contained on our site and intend to remove it, please contact our site administrator for approval.
© 2016-2026 All site design rights belong to S.Y.A.