NoSQL for Mere Mortals (2015)
Part V: Graph Databases
Chapter 14. Designing for Graph Databases
“We start with an idea which is then translated into a form, a structure.”
—LINDA VON DEURSEN
GRAPHIC DESIGNER, FACULTY YALE UNIVERSITY OF ART
Topics Covered In This Chapter
Getting Started with Graph Design
Querying a Graph
Tips and Traps of Graph Database Design
Case Study: Optimizing Transportation Routes
Graph database design has some things in common with other types of database design, but it has distinct characteristics as well. This chapter delves into details and examples of designing entity and relations between entities along with a description of two different ways of querying graph databases.
Graph databases have some unusual characteristics. Algorithms that run in reasonable time on small graphs can take a surprisingly long time with moderate or large graphs.
Design tips are included in this chapter to help you avoid, or at least recognize the potential for, such problems. This chapter concludes with a case study on the optimization of transportation routes.
Getting Started with Graph Design
A common characteristic of NoSQL databases is the way you approach design, which is by asking what kinds of queries or analysis you will perform on the data. Graph databases are well suited to problem domains that are easily described in terms of entities and relations between those entities.
Entities can be virtually anything, from proteins to planets. Of course, other NoSQL databases and relational databases are well suited to modeling entities, too.
What makes a particular problem well suited for a graph database? A number of characteristics.
Graph database applications frequently include queries and analysis that involve
• Identifying relations between two entities
• Identifying common properties of edges from a node
• Calculating aggregate properties of edges from a node
• Calculating aggregate values of properties of nodes
Here are some examples of each of these types of queries:
• How many hops (that is, edges) does it take to get from vertex A to vertex B?
• How many edges between vertex A and vertex B have a cost that is less than 100?
• How many edges are linked to vertex A?
• What is the centrality measure of vertex B?
• Is vertex C a bottleneck; that is, if vertex C is removed, which parts of the graph become disconnected?
![]() Note
Note
You might have noticed these queries are different from queries associated with document and column family databases. There is less emphasis on selecting by particular properties, for example, how many vertices have at least 10 edges? Similarly, there is less emphasis on aggregating values across a group of entities. For example, in a column family database, you might have a query that selects all customer orders from the Northeast placed in the last month and sum the total value of those orders. These types of queries can be done in graph databases, but they do not reflect the flexibility and new ways of querying offered by graph databases.
The queries listed above are fairly abstract. They are stated in the terminology used by computer scientists and mathematicians when working with graphs. When it comes to designing graph databases, it is probably better to start with queries that reflect the problem domain.
Designing a Social Network Graph Database
Imagine you are starting a new social networking site designed for NoSQL database developers. The goal is to support the NoSQL development community by providing a platform for sharing tips, asking questions, and keeping in touch with others working on similar problems. Let’s assume this site will allow for developers to
• Join and leave the site
• Follow the postings of other developers
• Post questions for others with expertise in a particular area
• Suggest new connections with other developers based on shared interests
• Rank members according to their number of connections, posts, and answers
The model will start simple with just two entities: developers and posts. You can always add more later, but it helps to flesh out the relations and properties of a small number of entities at a time.
Properties of developers include
• Name
• Location
• NoSQL databases used
• Years of experience with NoSQL databases
• Areas of interest, such as data modeling, performance tuning, and security
Developers will be asked for this information when they register at the site. Posts have several properties as well, such as
• Date created
• Topic keywords
• Post type (for example, question, tip, news)
• Title
• Body of post
The application will automatically assign date created as well as topic keywords. The person posting the message will fill in the other properties (see Figure 14.1).
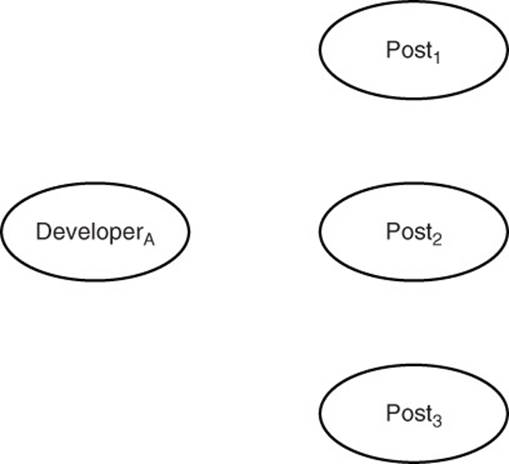
Figure 14.1 Developers and posts are two types of entities in the NoSQL social network.
Next, consider the relations between entities. Entities may have one or more relations to other entities. Because there are two types of entities, there can be four possible combinations of entity-relation-entity:
• Developer-relation-developer
• Developer-relation-post
• Post-relation-developer
• Post-relation-post
The term relation is a placeholder in the preceding list. As a graph database designer, one of your first tasks is to identify each of these relations.
![]() Tip
Tip
It helps to consider all possible combinations of entities having relations when the number of entity types is small. Some of the combinations may not be relevant to the types of queries you will pose. You can eliminate them from consideration. This process helps reduce the chance that you miss a relevant relation early in the design phase.
As the number of entities grows, you might want to focus on combinations that are reasonably likely to support your queries.
The “follows” relation is the only relation between developers in the simple model (see Figure 14.2). If Robert Smith follows Andrea Wilson, then Robert will see all of Andrea’s posts when he logs on to the NoSQL social network. The site designers believe the followers of a developer might be interested in who that developer follows as well. For example, if Andrea follows Charles Vita, then Robert should see Charles’s posts as well. You can imagine adding posts from the developers Charles follows, but that could start to overwhelm Robert’s feed.
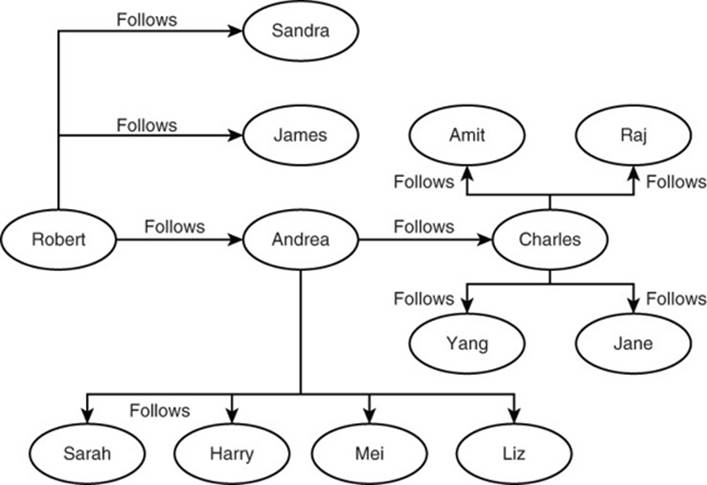
Figure 14.2 Sample set of “follows” relations in a NoSQL developer social network.
The designers do not have to decide now how deep of a path to pursue looking for posts to show to Robert. The way graph databases are designed makes it easy to alter application features with minor changes to queries. No change in the underlying model is required.
The relation between developers and posts is “created”; that is, developers create posts. This implies a reverse relationship; that is, that posts are “created by” developers. There are two ways to model this:
• A designer could create a directed edge of type “created” from the developer vertex to the post vertex and another directed edge from the post to the developer of type “created by,” as shown in Figure 14.3(a).
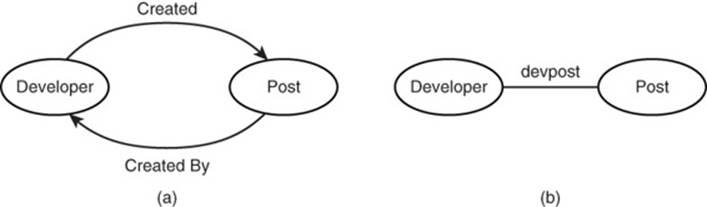
Figure 14.3 Developer and post with two directed edges (a); one edge not directed (b).
• Because one of these relations always implies the other, you can avoid using two directed edges by using a single, possibly undirected, edge, as shown in Figure 14.3(b).
Queries Drive Design (Again)
There is no one correct way to model a graph database for all possible problems. If you have queries that frequently involved gathering posts and then looking up the creators of those posts, it makes sense to have a created by relation.
By creating such an edge, you implement a direct link between the post and the developer. It is this feature that allows graph database designers to avoid working with joins to retrieve data from related entities. Following edges between vertices is a simple and fast operation, so it is possible to follow long paths or a large number of paths between vertices without adversely impacting performance.
At first glance, the post-relation-post may not appear useful. After all, posts do not create other posts. However, there is no rule that says all relations between entities need to be the same type. In fact, one of the powerful features of graph database modeling is the ability to use different types of relations. For example, a post may be created in response to another post. This is particularly useful for questions.
Imagine that Robert posted the question: Is there a faster way than Dijkstra’s algorithm to find the shortest path (see Figure 14.4)? Andrea and Charles might each reply with their own answers. Robert then posts another question to clarify his understanding of Andrea’s response. Andrea responds with additional details. Meanwhile, Edith Woolfe adds additional details to Charles’s post. The resulting graph of posts is a tree with Robert’s initial post as the root and branches that follow the two parts of the conversation thread.
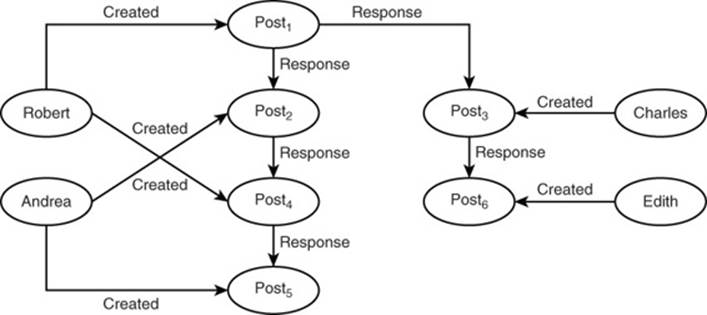
Figure 14.4 A conversation thread started with Robert posting a question.
Let’s return the queries that reference vertices and edges and rewrite them in terms of the NoSQL social network example.
As Table 14.1 shows, abstract queries map to useful queries about graph databases. Some queries are based on paths, such as the distance between two nodes; for example, “How many follows relations are between Developer A and Developer B?” Other queries take into account the global structure of the graph, such as “If a developer left the social network, would there be disconnected groups of developers?”
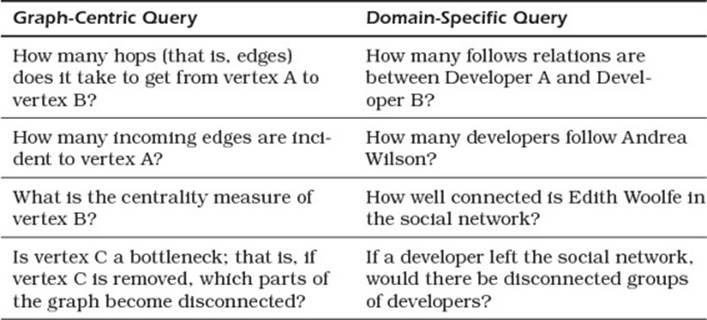
Table 14.1 Mapping from Graph-Specific Queries That Apply to Any Graph to Queries That Apply to a Social Network Graph
When you design graph databases, you start with domain-specific queries. Ultimately, you will want to map these domain-specific queries to graph-specific queries that reference vertices, edges, and graph measures, like centrality and betweenness.
When you have your domain-specific queries mapped to graph-specific queries, you have the full range of graph query tools and graph algorithms available to you to analyze and explore your data.
The following are the basic steps to getting started with graph database design:
• Identify the queries you would like to perform.
• Identify entities in the graph.
• Identify relations between entities
• Map domain-specific queries to more abstract queries so you can implement graph queries and use graph algorithms to compute additional properties of nodes.
Queries drive the design of graph databases. The next sections delve into details about how to perform those queries.
Querying a Graph
The motto of the Perl programing language is “There is more than one way to do it.” The same statement applies to querying graphs.
The Cypher query language provides a declarative, SQL-like language for building queries. Cypher is used with the Neo4j graph database (neo4j.com). Alternatively, developers can use Gremlin, a graph traversal language that works with a number of different graph databases.
The goal in this section is not to teach you the details of these query languages, but to give you a flavor for how each works and show examples of how each language is used.
Cypher: Declarative Querying
Before you can query a graph, you must create one. Cypher statements to create vertices for the preceding NoSQL social network include
CREATE (robert:Developer { name: 'Robert Smith' })
CREATE (andrea:Developer { name: 'Andrea Wilson' })
CREATE (charles:Developer { name: 'Charles Vita' })
These three statements create three vertices. The text robert: Developer creates a developer vertex with a label of robert. The text { name: 'Robert Smith' } adds a property to the node to store the name of the developer.
Edges are added with create statements as well. For example:
CREATE (robert)-[FOLLOWS]->(andrea)
CREATE (andrea)-[FOLLOWS]->(charles)
To query nodes in Cypher, use the MATCH command, which returns all developers in the social network:
MATCH (developer:DEVELOPER)
RETURN (developer)
A comparable query in SQL is
SELECT *
FROM developer
SQL is a declarative language designed to work with tables that consist of rows and columns. Cypher is a declarative language designed to work with graphs that consist of vertices and edges, so it is not surprising that there are ways to query based on both. For example, the following returns all developer nodes linked to Robert Smith:
MATCH (robert:Developer {name:'Robert
Smith'})--(developer:DEVELOPER)
RETURN developers
The MATCH operation starts with the node robert and searches all edges that lead to vertices of type DEVELOPER and returns those that it finds.
Cypher is a rich language with support for many graph operations. It also has clauses found in SQL, such as the following:
• WHERE
• ORDER BY
• LIMIT
• UNION
• COUNT
• DISTINCT
• SUM
• AVG
Because Cypher is a declarative query language, you specify the criteria for selecting vertices and edges, but you do not specify how to retrieve them. If you want control over the way your query retrieves vertices and edges, you should consider using a graph traversal language such as Gremlin.
Gremlin: Query by Graph Traversal
Traverse means to travel across or through. Graph traversal is the process of logically moving from one vertex to another over an edge. Instead of querying by specifying criteria for selecting vertices, as in Cypher, you specify vertices and rules for traversing them.
Basic Graph Traversal
Consider the graph in Figure 14.5. The graph has seven vertices and nine directed edges. Some vertices have edges coming in, some have only edges going out, and others have both.
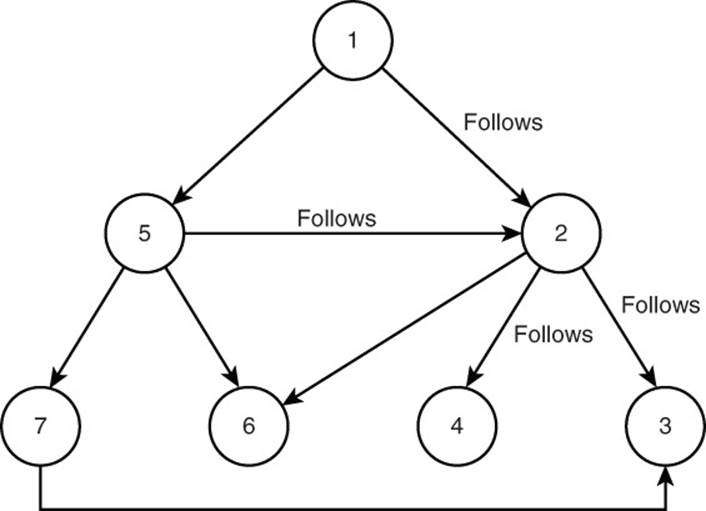
Figure 14.5 Sample directed graph with vertices with only in, out, and both in and out edges.
Let’s assume a graph G is defined with the vertices and edges shown in Figure 14.5. You can create a variable in Gremlin to refer to a particular vertex, such as
v = G.v(1)
Gremlin also has special terms defined to refer to adjacent edges and vertices. These are
• outE—Outgoing directed edges from a vertex
• inE—Incoming directed edges from a vertex
• bothE—Both inward and outward directed edges from a vertex
• outV—Outgoing vertex of an edge
• inV—Incoming vertex of an edge
• bothV—Both incoming and outgoing vertex of an edge
These are useful for querying edges and graphs based on a starting vertex or edge. For example, if you queried v.outE, you would get the following resultset:
[1-follows-2]
[1-follows-5]
Because the variable v is defined as the vertex v(1) and there are two outgoing edges, Gremlin returns a descriptive string representing those two edges.
Consider the following example:
v2 = G.v(2)
v2.outE
Results:
[2-follows-3]
[2-follows-4]
[2-follows-6]
The vertex 2 has five incident edges, but only three edges are listed above. This is because the other two edges are inbound edges, not outbound edges.
If you want to return the vertices at the end of the outbound edge, you can refer to the inbound vertices of the edges listed in the last example with the following code:
v2.outE.inV
Results:
[3]
[4]
[6]
This model of querying allows you to string together additional combinations of edge and vertex specifications, such as v2.outE.inV.outE.inV.
Gremlin supports more complex query patterns as well.
Traversing a Graph with Depth-First and Breadth-First Searches
There will be times when you do not have a specific starting point. Instead, you want to find all nodes that have a particular property. Cypher uses the MATCH statement for retrieving vertices.
In Gremlin, you can traverse the entire graph and as you visit each vertex, you can test it to determine if it meets your search criteria. For example, you could traverse the graph, starting at vertex 1 by visiting vertex 2, then vertex 3, then vertex 4, then vertex 5, then vertex 6, and finally vertex 7. This is an example of a depth-first search of a graph (see Figure 14.6).
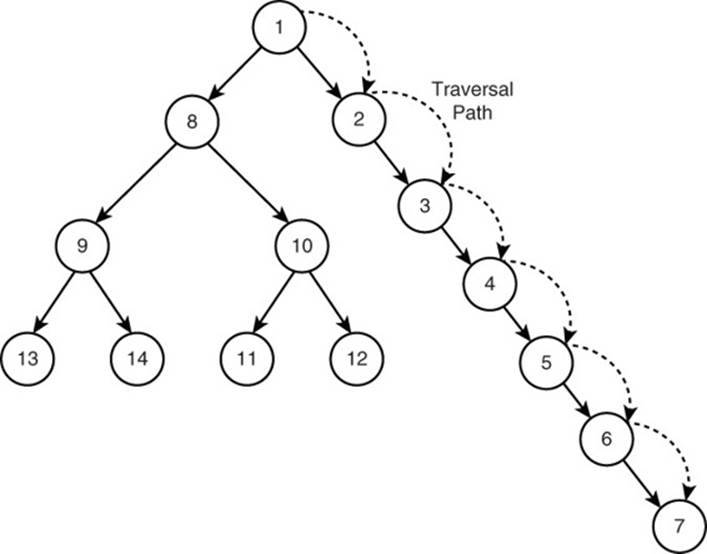
Figure 14.6 Example of a depth-first search.
In a depth-first search, you start traversal at one vertex and select adjacent vertices. You then select the first vertex in that resultset and select adjacent vertices to it. You continue to select the first vertex in the resultset until there are no more edges to traverse.
At that point, you visit the next vertex in the latest resultset. If there are incident edges leading to other vertices, you visit those; otherwise, you continue to the next item in the latest resultset. When you exhaust all vertices in the latest resultset, you return to the resultset selected prior to that and begin the process again.
In a breadth-first search, you visit each of the vertices incident to the current vertex before visiting other vertices. Figure 14.7 shows an example of a breadth-first search traversal.
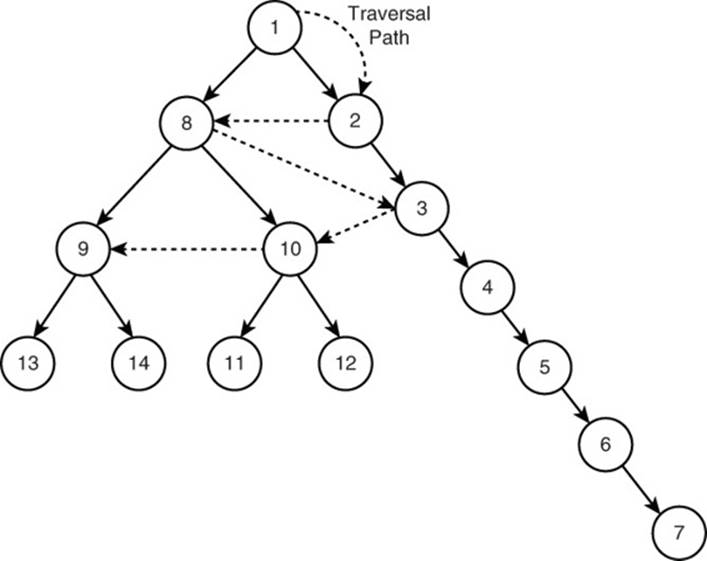
Figure 14.7 Example of a breadth-first search.
Gremlin supports other specialized types of graph traversal, such as the flow rank pattern that allows for queries such as “rank developers by the number of posts we have both commented on.”
![]() Note
Note
For details on the Gremlin language, see the Gremlin Wiki at https://github.com/tinkerpop/gremlin/wiki.
![]() Note
Note
Gremlin is part of the larger TinkerPop project that builds a common framework for graph databases and graph analysis applications. TinkerPop includes Blueprints, a database API analogous to JDBC and ODBC for relational databases; Pipes, a data flow framework for transforming streams of data; Furnace, a graph algorithm package; and Rexster, a graph server.
Graph databases support both declarative and traversal-based query methods. Choosing the more appropriate model will, as always, depend on your requirements.
Declarative languages, such as Cypher, are well suited to problems that require selecting vertices based on their properties. It is also useful when you need to apply aggregate operations, such as grouping or summing values from vertex properties.
Traversal languages, such as Gremlin, provide more control over how the query is executed. Developers, for example, can choose between searching by depth-first or breadth-first methods.
Tips and Traps of Graph Database Design
Applications using graph databases can take advantage of the vertexedge data model to implement efficient query and analysis capabilities. At the same time, graph operations that run in reasonable time with modest-size graphs may take too long to complete when the graph grows larger.
This section discusses several techniques that can be used to optimize performance when working with graphs.
Use Indexes to Improve Retrieval Time
Some graph databases provide for indexes on nodes. Neo4j, for example, provides a CREATE INDEX command that allows developers to specify properties to index. The Cypher query processor automatically uses indexes, when they are available, to improve the query performance ofWHERE and IN operations.
Use Appropriate Types of Edges
Edges may be directed or undirected. Directed edges are used when the relation between two vertices is not symmetrical. For example, in the NoSQL social network, Robert follows Andrea, but Andrea does not follow Robert. If Andrea were to follow Robert, there would be an additional edge, directed inward toward Robert from Andrea.
Undirected edges are used for symmetrical relations, such as the distance between two cities (see Figure 14.8).
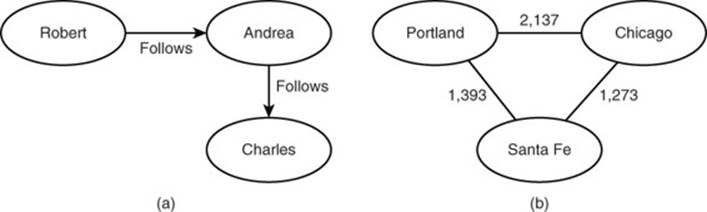
Figure 14.8 Undirected edges are used for symmetrical relations; directed edges are used for nonsymmetrical relations.
![]() Tip
Tip
Graph processing is memory intensive. Keep this in mind as you design your graph.
Simple edges with no properties require little storage, so there is not necessarily a storage penalty for using them. If, however, edges have a large number of properties or large values (for example, BLOBs), then the amount of storage required can be significant.
Consider whether your relations between two vertices require one undirected or two directed nodes. Also, consider how you code property values. Reducing the size of values that are used in a large number of edges can help reduce memory requirements.
Watch for Cycles When Traversing Graphs
Cycles are paths that lead back to themselves. The graph in Figure 14.9 has a cycle A-B-C-D-E-F-A.
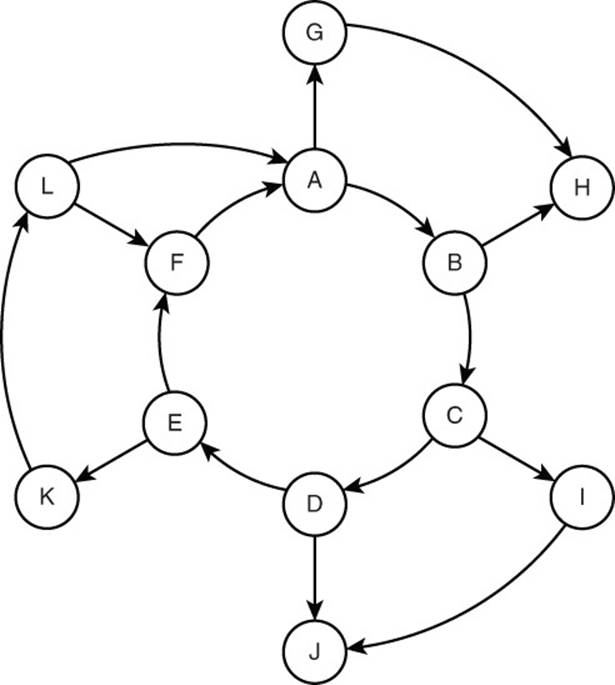
Figure 14.9 Cycles can cause problems with traversal if they are not accounted for in the traversal algorithm.
If you were to start a traversal at vertex A and then followed a path through vertices B, C, D, E, and F, you would end up back at A. If there is no indication that you have already visited A, you could find yourself in an endless cycle of revisiting the same six nodes over and over again.
![]() Tip
Tip
When writing your own graph-processing algorithms, consider the possibility of cycles. Not all graphs have them—trees, for example, do not.
If you might encounter cycles, keep track of which vertices have already been visited. This can be as simple as maintaining a set named visitedNodes.
Each time you visit a node, you first check to see if that node is in the set visitedNodes. If it is, you return with processing the node; otherwise, you process the node and add it to the set.
Consider the Scalability of Your Graph Database
The graph database systems available today can work with millions of vertices and edges using a single server. You should consider how your applications and analysis tools will scale as the following occurs:
• The number of nodes and edges grow
• The number of users grow
• The number and size of properties on vertices and edges grow
Increases in each of these three areas can put additional demands on a database server. Many graph databases are designed to run on a single server. If your server can no longer meet performance requirements, you have to scale vertically, that is, get a bigger server.
![]() Note
Note
This is an unusual situation for NoSQL databases, which are generally designed for scalability. Titan (http://thinkaurelius.github.io/titan/), a graph database designed to scale horizontally—that is, by adding more servers—uses other NoSQL databases such as Cassandra for basic storage and retrieval functions. Because Titan supports Gremlin and the TinkerPop graph platform, you could start with another graph database that supports Gremlin and migrate to Titan when you need to horizontally scale.
Also consider the algorithms you use to analyze data in the graph. The time required to perform some types of analysis grows rapidly as you add more vertices. For example, Dijkstra’s algorithm for finding the shortest paths in a network takes a time related to the square of the number of vertices in a graph.
To find the largest group of people who all follow each other (known as a maximal clique) in the NoSQL social network requires time that grows exponentially with the number of people.
Table 14.2 shows examples of time required to run Dijkstra’s algorithm and solve the maximal clique problem. Be careful when using graph algorithms. Some that run in reasonable amounts of time with small graphs will not finish in reasonable amounts of time if the graphs grow too large. This table assumes a time of two units to complete the operations on a single vertex.
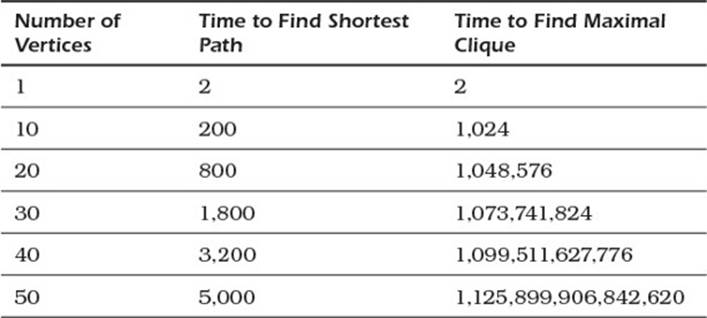
Table 14.2 Solving a Maximal Clique Problem
Summary
Graph databases are well suited to a wide range of applications. Graph database designers should start with the queries they will run on the database to identify the entities and relations between entities that should be modeled. Depending on the types of relations, edges may be directed or undirected.
Graph databases support both declarative and traversal query options. Designers should use optimization features, such as indexes, when available to improve the overall performance of graph database operations.
Case Study: Optimizing Transportation Routes
A client of TransGlobal Transport and Shipping (TGTS), a fictitious transportation company, has hired the analytics company to help optimize its shipping routes. The client ships parcels from manufacturing sites to distribution centers and then to customer sites. It has used a simple method for shipping parcels but suspects its approach is less than optimal.
Understanding User Needs
Analysts at TGTS have several meetings with executives, shipping managers, and other employees responsible for parcel shipping. They learn that the client uses two methods for shipping:
• If there is no need for rush shipping, an employee from the manufacturing site will drive a shipment of parcels to the nearest hub airport. From there, it is flown to a distribution center closest to the ultimate customer destination. An employee from the distribution center then drives the package from the distribution center to the customer’s location.
• If there is a rush order, an employee from the manufacturing site drives the shipment to the closest regional airport and the parcel is flown to the closet regional airport to the customer.
The client has data indicating that the first method is less expensive than the second, which is only used in order to meet time constraints on delivery.
The analysts collect information about the client’s shipping costs between all of its facilities and its customer sites.
Designing a Graph Analysis Solution
The TGTS analysts quickly realize that the client is using only a small subset of all possible routes. They determine that Dijkstra’s algorithm can be used with data from a graph database to find the least-cost path between all locations.
The set of least-cost paths will provide the optimal route for deliveries without time constraints. It does not, however, address the need to consider time constraints as well as costs.
The analysts decide to use edge properties to store both the cost of moving a parcel between the two locations and the time required to move it.
![]() Tip
Tip
Because the cost of shipping a parcel will vary by weight, the TGTS analysts use a unit cost, such as cost per kilogram, to represent the cost of the edge.
The time property is the average time it takes to ship a parcel between locations. The client has historical data for many of the edges, but not all. For those edges without shipment time data, the analysts estimate based on the shipping time of packages between similar types of facilities.
The TGTS analysts create a database of shortest paths between all facilities and store the total cost and total time required to ship a parcel. They realize that sometimes the least-cost path will not meet time constraints on delivery, so the analysts develop their own algorithm to find the least-cost path that does meet the time constraints.
The algorithm takes as input a start facility, an end facility, and the time available for delivery. As the algorithm traverses each facility (vertex), it records the cumulative cost and time required to ship a parcel between the two facilities. If at any time, the cumulative time exceeds the time available for delivery, the path is discarded.
All remaining paths are stored in a list sorted by cost. The first path in the list is the least-cost path created so far. The algorithm continues with the least-cost path and finds all facilities linked to the latest facility in the least-cost path.
If any of those facilities is the final destination, the algorithm terminates and outputs the least-cost path with a delivery time within constraints. Otherwise, it continues to find facilities linked to the last facility in the current least-cost path.
As this example shows, well-established algorithms can provide the foundation for graph analysis problems. There are times, however, that slight variations on the algorithm are required to accommodate the particular requirements of the problem under study.
Review Questions
1. What is the benefit of mapping domain-specific queries into graph-specific queries?
2. Which is more like SQL, Cypher or Gremlin?
3. How is the MATCH statement like a SQL SELECT statement?
4. What are the inE and outE terms used for in Gremlin?
5. Which type of edge should be used for a nonsymmetrical relation, a directed or undirected edge?
6. What is the difference between a declarative and a traversal query language for graph databases?
7. What is a depth-first search?
8. What is a breadth-first search?
9. Why are cycles a potential problem when performing graph operations?
10. Why is scalability such an important consideration when working with graphs?
References
Gremlin: https://github.com/tinkerpop/gremlin/wiki
Neo4j Manual: http://neo4j.com/docs/
Titan Distributed Graph Database: http://thinkaurelius.github.io/titan/
Wikipedia. “Dijkstra’s Algorithm”: http://en.wikipedia.org/wiki/Dijkstra%27s_algorithm