Java: Artificial Intelligence; Made Easy, w/ Java Programming; Learn to Create your * Problem Solving * Algorithms! TODAY! w/ Machine Learning & Data Structures, 1st Edition (2015)
Chapter 2. How to Create a Problem-Solving AI
==== ==== ==== ==== ====
Let’s start developing our Search algorithm: an automatic problem solver. We’ll have a general overview of it in Pseudocode. Then you’ll get to code and run it on your own, with this book’s primary programming language.
Abstract Search Algorithm
In its most basic procedure, a search algorithm will have a default condition and a goal condition. It will then evaluate each option it can take, starting from the default condition, step-by-step, until it eventually finds a full set of options to achieve the goal condition.
The General Frontier Search Algorithm:
The Frontier Search algorithm follows the same procedure as above. Given a start node, goal nodes, and an entire network, it will incrementally assess and explore pathways from the start node until it reaches the goal node.
The Frontier is simply a list of paths to be checked. The Frontier Search algorithm will keep adding paths to the Frontier until it either finds a solution or has explored the entire network
For example, this is just like giving a Search Algorithm a map of your local city, your current location, and a restaurant you’re about to go to. That search algorithm will give you directions to get there.
The standard data structure to use a Search Algorithm with is a Network of interconnected Nodes. Each node contains an amount of data and a list of connected nodes:
// A Node has:
// - its data (any data type you want)
// - a set of connected nodes
class Node
<some data type>: contents
Array of Nodes: connected
The Frontier Search algorithm also uses Paths: a list of connected Nodes, with the first node as the starting point:
// A Path has:
// - a List of Nodes
class Path
Array of Paths: contents
And finally, here is a generalized algorithm for Frontier Search:
INPUT:
- a Start Node (can be a class method in OOP)
- a graph network (only requires start node to have a network)
- a goal-checking procedure OR a solution query
OUTPUT:
- a Path from start to Goal (a List of Nodes)
- return FALSE or NULL if no paths found (wherever applicable)
EFFECT:
Frontier Search Algorithm: Returns a set of nodes that lead from the input Node to a solution node if found
PROCEDURE:
- frontier:= {new array of Nodes}
- create a new Path and put the Start node in it
- put the new Path into the frontier
While frontier is not empty {
- select and remove a Path <s0, s1,….,sk> from frontier;
If node (sk) is a goal, return selected Path <s0, s1, ….,sk>;
Else:
For every connected node of end node sk:
- Make a copy of the selected Path
- Add connected node of sk onto path copy
- add copied Path <s0, s1,….,sk, s> to frontier;
}
- indicate ‘NO SOLUTION’ if frontier empties
Further Search Strategies
This will be covered later on, but how the algorithm picks a Path from the Frontier will determine how the Search Algorithm works.
For now, let’s apply the Frontier Search Algorithm.
JAVA 02a: Fundamental Frontier Search Algorithm
For the procedure below, select an IDE of your choice. You may also use online IDE’s such as rextester.com, ideone.com, or codepad.org.
========================= ======
Below are the fundamental parts to a Frontier Search algorithm: the major algorithm and its data structures.
First, we start with the Data Structures. We only need to use two essential classes: a network node and a path. A Path contains is what the algorithm uses to store connected, sequenced nodes. It will also be the output type for the algorithm.
// A Path has:
// - A List of Nodes
// (can be modified to include more Methods/Fields)
class Path {
ArrayList<Node> contents = new ArrayList<Node>();
}
Nodes will be the main data structure the Algorithm will operate through; the algorithm will search through the node and its connected nodes for a solution:
// A Node has:
// - Some Contents (Data type of your choice)
// - A List of other connected Nodes
// It can:
// - Search all its descendant nodes to find a solution
// (Our Search Algorithm as a Class Method)
class Node {
<choose a data type> contents;
ArrayList<Node> children;
// CONSTRUCTOR:
public Node(String c) {
this.contents = c;
this.children = new ArrayList<Node>();
}
}
Next are two Helper Functions you’ll need. This first function helps the algorithm pick a path to check from a list:
/*
// HELPER FUNCTION #1:
// INPUT: a List of Paths
// OUTPUT: a Single Path
// EFFECT: based on positioning of your choice:
// - Select & remove a path
// - return that path
// NOTE: you can modify the position assignment to change the Search Strategy
*/
private Path pickPath(ArrayList<Path> f) {
int position = 0;
Path ret = f.get(position);
f.remove(position);
return ret;
}
This second function checks if the last node in the path is a solution. One of the function inputs supplies the solution:
/*
// HELPER FUNCTION #2:
// INPUTs:
// - a Path
// - Node contents that have a solution
// <same data type as Node’s container>
// OUTPUT: boolean
// EFFECT: outputs True if path contains a Goal
*/
private boolean hasGoal(<data type> s, Path p) {
for (Node n: p.contents) {
if (n.contents == s) return true;
}
return false;
}
And finally, the Search Algorithm. The pseudocode is attached to the lines as comments so you can see how the procedure works. The algorithm also uses both helper functions described earlier.
/*
// MAIN ALGORITHM:
// INPUT:
// - a goal query
// <has same data type as node contents>
// - a Starting Node
// OUTPUT:
// - a Path from start to Goal (a List of Nodes)
// (multiple output types not acceptable in Java;
// empty Path as output if no solution found)
// EFFECT:
// Frontier Search Algorithm: Returns a set of
// nodes that lead from the input Node to a solution node if found
*/
public Path search(<data type> query, Node n1) {
// - frontier:= {new array of Paths}
ArrayList<Path> frontier = new ArrayList<Path>();
// - create a new Path and put the Start node in it
Path p = new Path();
p.contents.add(n1);
// - put the new Path into the frontier
frontier.add(p);
while (!frontier.isEmpty()) {
// - select and remove a Path <s0, s1,….,sk> from frontier;
// (use helper function pickPath() )
Path pick = pickPath(frontier);
// If node (sk) is a goal, return selected Path
if (hasGoal(query, pick)) {
return pick;
}
else {
// Otherwise, for every connected node of end node sk:
// 1. Make a copy of the selected Path
// 2. Add connected node of sk onto path copy
// 3. add copied Path <s0, s1,….,sk, s> to frontier;
int size = pick.contents.size();
Node last = pick.contents.get(size - 1);
for (Node n: last.children) {
Path toAdd = new Path();
toAdd.contents.addAll(pick.contents);
toAdd.contents.add(n);
frontier.add(toAdd);
}
}
}
// - indicate ‘NO SOLUTION’ if frontier empties
// (empty path as 'NO SOLUTION' here)
return new Path();
}
JAVA 02b: Using Frontier Search
For the procedure below, select an IDE of your choice. You may also use online IDE’s such as rextester.com, ideone.com, or codepad.org.
========================= ======
Here, we implement the Frontier Search Algorithm step-by-step onto a simple node network: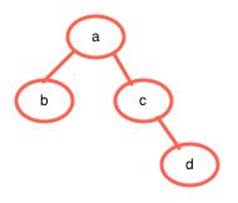
Each circle a, b, c, and d each represent interconnected nodes, which will only have their respective letters as contents.
We ask the algorithm if there is a path to a particular letter from a starting point.
The Search Algorithm would have a letter as an input. It would then check the nodes row-by-row until it either finds a suitable path from the input node to that letter - or notify you that a path couldn’t be found.
So we now know what to expect. If we have, say ,’d’ as the input, the algorithm is supposed to find it, and output the node path a->c->d. If we have ‘g’ or some other irrelevant letter as an input, the algorithm will say that it’s not found.
Artificial Intelligence will heavily rely on Search Algorithms to come up with solutions and best decisions for its given situations. We will explore more about this later on.
Meanwhile, let’s start building our algorithm.
Step 1: Understand & Create the Node Structure
First, we have to build the underlying data structure for our Network. Our Nodes contain the data type we want to use, as well as a list of its connected nodes. Since we’re only using letters, our Node data type can be String.
Copy the class code below to your IDE. We’ll build on from here.
// A Node has:
// - Some Contents (Data type of your choice)
// - A List of other connected Nodes
// It can:
// - Search all its descendant nodes to find a solution
// (Our Search Algorithm as a Class Method)
class Node {
String contents;
ArrayList<Node> children;
// CONSTRUCTOR:
public Node(String c) {
this.contents = c;
this.children = new ArrayList<Node>();
}
}
Afterwards, we need the node network.
the node network.
So it looks like ‘d’ is a connected to ‘c’, while ‘b’ and ‘c’ are connected to ‘a’. We’ll be re-creating this network in code.
Copy the code below and place it within the main() method:
// Creates & connects nodes a, b, c, d
Node a = new Node("a");
Node b = new Node("b");
Node c = new Node("c");
Node d = new Node("d");
a.children.add(b);
a.children.add(c);
c.children.add(d);
Next, we need to design the Path.
Step 2: Create the Path Structure
The Path will contain an ordered list of Nodes. Each node will be connected to the ones next to it, while the first node in the Path is the Start node.
Copy the class code below to your IDE, just before where you put the Node class.
// A Path has:
// - A List of Nodes
// (can be modified to include more Methods/Fields)
class Path {
ArrayList<Node> contents = new ArrayList<Node>();
}
Step 3: Start coding the Algorithm
(Before we move forward, it’s highly recommended to review the Algorithm procedure in the past few chapters.)
Here, our search algorithm will be a method from the Node class. We can simply access it from one of the nodes created. And since we’re doing it this way, we won’t have to use a Node object as an input.
Since we are checking for letters, the search query will be a String - the same data type for the Node containers.
Place the Main Algorithm below within the Node Class you’ve created. Remember to have it within the curly brackets ‘{ }’.
/*
// MAIN ALGORITHM:
// INPUT:
// - a goal query
// <has same data type as node contents>
//
// (Start Node & its graph network accessed thru this method)
// OUTPUT:
// - a Path from start to Goal (a List of Nodes)
// (multiple output types not acceptable in Java;
// empty Path as output if no solution found)
// EFFECT:
// Frontier Search Algorithm: Returns a set of
// nodes that lead from the input Node to a solution node if found
*/
public Path search(String query) {
// - frontier:= {new array of Nodes}
ArrayList<Path> frontier = new ArrayList<Path>();
// - create a new Path and put the Start node in it
Path p = new Path();
p.contents.add(this);
// - put the new Path into the frontier
frontier.add(p);
while (!frontier.isEmpty()) {
// - select and remove a Path <s0, s1,….,sk> from frontier;
// (use helper function pickPath() )
Path pick = pickPath(frontier);
// If node (sk) is a goal, return selected Path
if (hasGoal(query, pick)) {
return pick;
}
else {
// For every connected node of end node sk:
// - Make a copy of the selected Path
// - Add connected node of sk onto path copy
// - add copied Path <s0, s1,….,sk, s> to frontier;
int size = pick.contents.size();
Node last = pick.contents.get(size - 1);
for (Node n: last.children) {
Path toAdd = new Path();
toAdd.contents.addAll(pick.contents);
toAdd.contents.add(n);
frontier.add(toAdd);
}
}
}
// - indicate ‘NO SOLUTION’ if frontier empties
// (empty path as 'NO SOLUTION' here)
return new Path();
}
It’s considered a good programming practice to simplify what a function does. So instead of our algorithm function doing a lot of different things, it will call specialized helper functions to simplify the workload. This also makes it easier for programmers to check, edit, debug, and modify the code.
Step 4: Add the Frontier Path Picker Function
The path picking function for the Frontier Search algorithm is a customizable one in it own right, as modifying this function will affect the search strategy. We’ll go over more search strategies later on. For now, just ensure that the function selects, removes, and outputs the path correctly.
Place this helper function within the same Node class you placed the Search Algorithm.
/*
// HELPER FUNCTION #1:
// INPUT: a List of Paths
// OUTPUT: a Single Path
// EFFECT: based on positioning of your choice:
// - Select & remove a path
// - return that path
// NOTE: you can modify the position assignment to change the Search Strategy
*/
private Path pickPath(ArrayList<Path> f) {
int position = 0;
Path ret = f.get(position);
f.remove(position);
return ret;
}
Step 5: Add the Goal-checking Function
This function helps the algorithm check a path for solutions. It will check all the nodes in a path to see if one of them has the contents the algorithm is looking for.
Since both our node contents and search query are Strings, we’ll use that data type as a function input.
Like the other helper function, place this one within the same Node class you placed the Search Algorithm.
/*
// HELPER FUNCTION #2:
// INPUTs:
// - a Path
// - Node contents that have a solution
// <same data type as Node’s container>
// OUTPUT: boolean
// EFFECT: outputs True if path contains a Goal
*/
private boolean hasGoal(String s, Path p) {
for (Node n: p.contents) {
if (n.contents == s) return true;
}
return false;
}
Algorithm Testing
And finally, we test our algorithm. There’s at least three major scenarios to think of: searching for the starting node’s letter; searching for a letter further down the network; and searching for a letter that’s not in the network. For each of these times, we want the algorithm to run through the scenario properly.
Within your Main Class, and just above your main() method, insert this testing method:
static String printer(Path p) {
if (p.contents.isEmpty()) return "NOTE: No Solution Found";
else {
// System.out.println("FOUND A SOLUTION!");
String s = "Solution Found! Path: ";
for (int i = 0; i<p.contents.size(); i++) {
s += p.contents.get(i).contents + ", ";
}
return s;
}
}
Afterwards, we’ll create a few paths generated from our Search Algorithm. Place the code below just after your node network from Step 1. They should be inside the main() method.
// test search()
Path pa = a.search("a");
Path pc = a.search("c");
Path pd = a.search("d");
Path pg = a.search("g");
A search for the starting node’s letter should output a Path with just the starting node. So Path ‘pa’ should have a path with only node ‘a’ in it. If everything was done right, the code below should print out, “Solution Found! Path: a, ”.
System.out.println(printer(pa));
A search for a letter somewhere down the network should output a Path with a sequenced list of Nodes. Paths ‘pc’ and ‘pd’ should have nodes ‘a, c’ and ‘a, c, d’ respectfully. If the codes below run, then they should print out their respective paths:
System.out.println(printer(pc));
System.out.println(printer(pd));
A search for a letter that isn’t in the network should output an empty path, according to our current Search algorithm. So ‘pg’ should be an empty path.
If you run the line of code below, it should notify you that a solution isn’t found (‘g’ currently isn’t in the network)
System.out.println(printer(pg));
And there we have it. A successfully operating Frontier Search algorithm.