Java SE 8 for the Really Impatient (2014)
Chapter 3. Programming with Lambdas
Topics in This Chapter
![]() 3.1 Deferred Execution
3.1 Deferred Execution
![]() 3.2 Parameters of Lambda Expressions
3.2 Parameters of Lambda Expressions
![]() 3.3 Choosing a Functional Interface
3.3 Choosing a Functional Interface
![]() 3.4 Returning Functions
3.4 Returning Functions
![]() 3.5 Composition
3.5 Composition
![]() 3.6 Laziness
3.6 Laziness
![]() 3.7 Parallelizing Operations
3.7 Parallelizing Operations
![]() 3.8 Dealing with Exceptions
3.8 Dealing with Exceptions
![]() 3.9 Lambdas and Generics
3.9 Lambdas and Generics
![]() 3.10 Monadic Operations
3.10 Monadic Operations
![]() Exercises
Exercises
In the first two chapters, you saw the basic syntax and semantics of lambda expressions as well as the stream API that makes extensive use of them. In this chapter, you will learn how to create your own libraries that make use of lambda expressions and functional interfaces.
The key points of this chapter are:
• The main reason for using a lambda expression is to defer the execution of the code until an appropriate time.
• When a lambda expression is executed, make sure to provide any required data as inputs.
• Choose one of the existing functional interfaces if you can.
• It is often useful to write methods that return an instance of a functional interface.
• When you work with transformations, consider how you can compose them.
• To compose transformations lazily, you need to keep a list of all pending transformations and apply them in the end.
• If you need to apply a lambda many times, you often have a chance to split up the work into subtasks that execute concurrently.
• Think what should happen when you work with a lambda expression that throws an exception.
• When working with generic functional interfaces, use ? super wildcards for argument types, ? extends wildcards for return types.
• When working with generic types that can be transformed by functions, consider supplying map and flatMap.
3.1. Deferred Execution
The point of all lambdas is deferred execution. After all, if you wanted to execute some code right now, you’d do that, without wrapping it inside a lambda. There are many reasons for executing code later, such as
• Running the code in a separate thread
• Running the code multiple times
• Running the code at the right point in an algorithm (for example, the comparison operation in sorting)
• Running the code when something happens (a button was clicked, data has arrived, and so on)
• Running the code only when necessary
It is a good idea to think through what you want to achieve when you set out programming with lambdas.
Let us look at a simple example. Suppose you log an event:
logger.info("x: " + x + ", y: " + y);
What happens if the log level is set to suppress INFO messages? The message string is computed and passed to the info method, which then decides to throw it away. Wouldn’t it be nicer if the string concatenation only happened when necessary?
Running code only when necessary is a use case for lambdas. The standard idiom is to wrap the code in a no-arg lambda:
() -> "x: " + x + ", y: " + y
Now we need to write a method that
1. Accepts the lambda
2. Checks whether it should be called
3. Calls it when necessary
To accept the lambda, we need to pick (or, in rare cases, provide) a functional interface. We discuss the process of choosing an interface in more detail in Section 3.3, “Choosing a Functional Interface,” on page 50. Here, a good choice is a Supplier<String>. The following method provides lazy logging:
public static void info(Logger logger, Supplier<String> message) {
if (logger.isLoggable(Level.INFO))
logger.info(message.get());
}
We use the isLoggable method of the Logger class to decide whether INFO messages should be logged. If so, we invoke the lambda by calling its abstract method, which happens to be called get.
![]() NOTE
NOTE
Deferring logging messages is such a good idea that the Java 8 library designers beat me to it. The info method, as well as the other logging methods, now have variants that accept a Supplier<String>. You can directly call logger.info(() -> "x: " + x + ", y:" + y). However, see Exercise 1 for a potentially useful refinement.
3.2. Parameters of Lambda Expressions
When you ask your user to supply a comparator, it is pretty obvious that the comparator has two arguments—the values to be compared.
Arrays.sort(names,
(s, t) -> Integer.compare(s.length(), t.length())); // Compare strings s and t
Now consider a different example. This method repeats an action multiple times:
public static void repeat(int n, IntConsumer action) {
for (int i = 0; i < n; i++) action.accept(i);
}
Why an IntConsumer and not a Runnable? We tell the action in which iteration it occurs, which might be useful information. The action needs to capture that input in a parameter
repeat(10, i -> System.out.println("Countdown: " + (9 - i)));
Another example is an event handler
button.setOnAction(event -> action);
The event object carries information that the action may need.
In general, you want to design your algorithm so that it passes any required information as arguments. For example, when editing an image, it makes sense to have the user supply a function that computes the color for a pixel. Such a function might need to know not just the current color, but also where the pixel is in the image, or what the neighboring pixels are.
However, if these arguments are rarely needed, consider supplying a second version that doesn’t force users into accepting unwanted arguments:
public static void repeat(int n, Runnable action) {
for (int i = 0; i < n; i++) action.run();
}
This version can be called as
repeat(10, () -> System.out.println("Hello, World!"));
3.3. Choosing a Functional Interface
In most functional programming languages, function types are structural. To specify a function that maps two strings to an integer, you use a type that looks something like Function2<String, String, Integer> or (String, String) -> int. In Java, you instead declare the intent of the function, using a functional interface such as Comparator<String>. In the theory of programming languages this is called nominal typing.
Of course, there are many situations where you want to accept “any function” without particular semantics. There are a number of generic function types for that purpose (see Table 3–1), and it’s a very good idea to use one of them when you can.
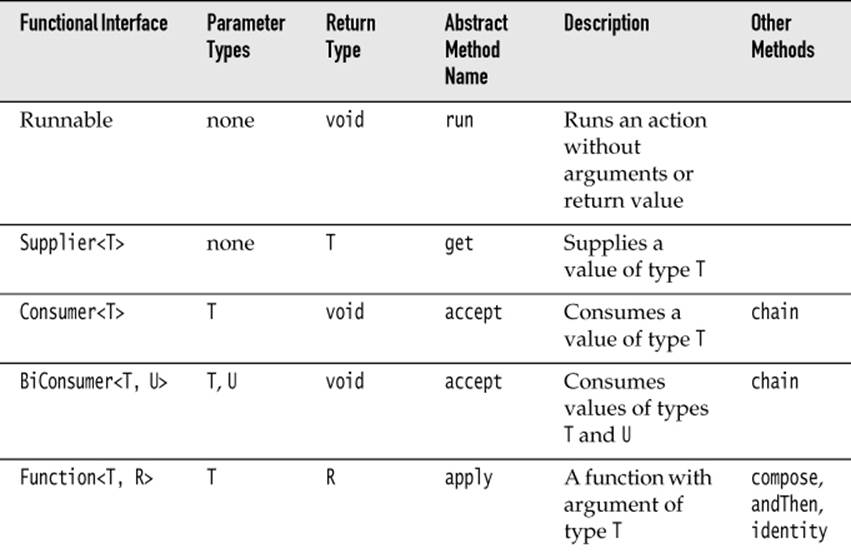
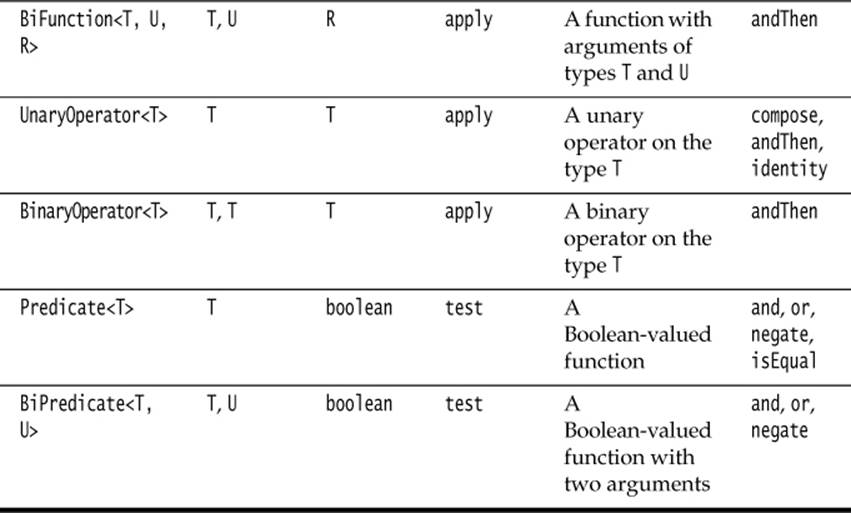
Table 3–1 Common Functional Interfaces
For example, suppose you write a method to process files that match a certain criterion. Should you use the descriptive java.io.FileFilter class or a Predicate<File>? I strongly recommend that you use the standard Predicate<File>. The only reason not to do so would be if you already have many useful methods producing FileFilter instances.
![]() NOTE
NOTE
Most of the standard functional interfaces have nonabstract methods for producing or combining functions. For example, Predicate.isEqual(a) is the same as a::equals, provided a is not null. And there are default methods and, or, negate for combining predicates. For example, Predicate.isEqual(a). or(Predicate.isEqual(b)) is the same as x -> a.equals(x) || b.equals(x).
Consider another example. We want to transform images, applying a Color -> Color function to each pixel. For example, the brightened image in Figure 3–1 is obtained by calling
Image brightenedImage = transform(image, Color::brighter);

Figure 3–1 The original and transformed image
There is a standard functional interface for this purpose: UnaryOperator<Color>. That is a good choice, and there is no need to come up with a ColorTransformer interface.
Here is the implementation of the transform method. Note the call to the apply method.
public static Image transform(Image in, UnaryOperator<Color> f) {
int width = (int) in.getWidth();
int height = (int) in.getHeight();
WritableImage out = new WritableImage(width, height);
for (int x = 0; x < width; x++)
for (int y = 0; y < height; y++)
out.getPixelWriter().setColor(x, y,
f.apply(in.getPixelReader().getColor(x, y)));
return out;
}
![]() NOTE
NOTE
This method uses the Color and Image classes from JavaFX, not from java.awt. See Chapter 4 for more information on JavaFX.
Table 3–2 lists the 34 available specializations for primitive types int, long, and double. Use the specializations when you can to reduce autoboxing.
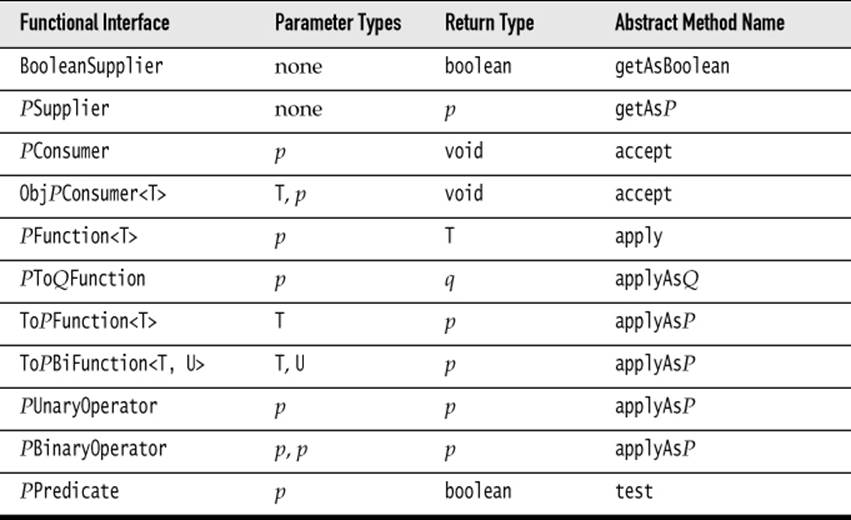
p, q is int, long, double;
P, Q is Int, Long, Double
Table 3–2 Functional Interfaces for Primitive Types
Sometimes, you need to supply your own functional interface because there is nothing in the standard library that works for you. Suppose you want to modify colors in an image, allowing users to specify a function (int, int, Color) -> Color that computes a new color depending on the (x, y) location in the image. In that case, you can define your own interface:
@FunctionalInterface
public interface ColorTransformer {
Color apply(int x, int y, Color colorAtXY);
}
![]() NOTE
NOTE
I called the abstract method apply because that is used for the majority of standard functional interfaces. Should you call the method process or transform or getColor instead? It doesn’t matter much to users of the color manipulation code—they will usually supply a lambda expression. Sticking with the standard name simplifies the life of the implementor.
3.4. Returning Functions
In a functional programming language, functions are first-class citizens. Just like you can pass numbers to methods and have methods that produce numbers, you can have arguments and return values that are functions. This sounds abstract, but it is very useful in practice. Java is not quite a functional language because it uses functional interfaces, but the principle is the same. You have seen many methods that accept functional interfaces. In this section, we consider methods whose return type is a functional interface.
Consider again image transformations. If you call
Image brightenedImage = transform(image, Color::brighter);
the image is brightened by a fixed amount. What if you want it even brighter, or not quite so bright? Could you supply the desired brightness as an additional parameter to transform?
Image brightenedImage = transform(image,
(c, factor) -> c.deriveColor(0, 1, factor, 1), // Brighten c by factor
1.2); // Use a factor of 1.2
One would have to overload transform:
public static <T> Image transform(Image in, BiFunction<Color, T> f, T arg)
That can be made to work (see Exercise 6), but what if one wants to supply two arguments? Or three? There is another way. We can make a method that returns the appropriate UnaryOperator<Color>, with the brightness set:
public static UnaryOperator<Color> brighten(double factor) {
return c -> c.deriveColor(0, 1, factor, 1);
}
Then we can call
Image brightenedImage = transform(image, brighten(1.2));
The brighten method returns a function (or, technically, an instance of a functional interface). That function can be passed to another method (here, transform) that expects such an interface.
In general, don’t be shy to write methods that produce functions. This is useful to customize the functions that you pass to methods with functional interfaces. For example, consider the Arrays.sort method with a Comparator argument. There are many ways of comparing values, and you can write a method that yields a comparator for your needs—see Exercise 7. Then you can call Arrays.sort(values, comparatorGenerator(customization arguments)).
![]() NOTE
NOTE
As you will see in Chapter 8, the Comparator class has several methods that yield or modify comparators.
3.5. Composition
A single-argument function transforms one value into another. If you have two such transformations, then doing one after the other is also a transformation. Consider image manipulation: Let’s first brighten an image, then turn it to grayscale (see Figure 3–2).

Figure 3–2 First, the image is brightened, and then grayscale is applied.
![]() NOTE
NOTE
In the printed book, everything is in grayscale. Just run the program in the companion code to see the effect.
That is easy to do with our transform method:
Image image = new Image("eiffel-tower.jpg");
Image image2 = transform(image, Color::brighter);
Image finalImage = transform(image2, Color::grayscale);
But this is not very efficient. We need to make an intermediate image. For large images, that requires a considerable amount of storage. If we could compose the image operations and then apply the composite operation to each pixel, that would be better.
In this case, the image operations are instances of UnaryOperator<Color>. That type has a method compose that, for rather depressing reasons that are explored in Exercise 10, is not useful for us. But it is easy to roll our own:
public static <T> UnaryOperator<T> compose(UnaryOperator<T> op1,
UnaryOperator<T> op2) {
return t -> op2.apply(op1.apply(t));
}
Now we can call
Image finalImage = transform(image, compose(Color::brighter, Color::grayscale));
That is much better. Now the composed transformation is directly applied to each pixel, and there is no need for an intermediate image.
Generally, when you build a library where users can carry out one effect after another, it is a good idea to give library users the ability to compose these effects. See Exercise 11 for another example.
3.6. Laziness
In the preceding section, you saw how users of an image transformation method can precompose operations to avoid intermediate images. But why should they have to do that? Another approach is for the library to accumulate all operations and then fuse them. This is, of course, what the stream library does.
If you do lazy processing, your API needs to distinguish between intermediate operations, which accumulate the tasks to be done, and terminal operations which deliver the result. In the image processing example, we can make transform lazy, but then it needs to return another object that is not an Image. For example,
LatentImage latent = transform(image, Color::brighter);
A LatentImage can simply store the original image and a sequence of image operations.
public class LatentImage {
private Image in;
private List<UnaryOperator<Color>> pendingOperations;
...
}
This class also needs a transform method:
LatentImage transform(UnaryOperator<Color> f) {
pendingOperations.add(f);
return this;
}
To avoid duplicate transform methods, you can follow the approach of the stream library where an initial stream() operation is required to turn a collection into a stream. Since we can’t add a method to the Image class, we can provide a LatentImage constructor or a static factory method.
LatentImage latent = LatentImage.from(image)
.transform(Color::brighter).transform(Color::grayscale);
You can only be lazy for so long. Eventually, the work needs to be done. We can provide a toImage method that applies all operations and returns the result:
Image finalImage = LatentImage.from(image)
.transform(Color::brighter).transform(Color::grayscale)
.toImage();
Here is the implementation of the method:
public Image toImage() {
int width = (int) in.getWidth();
int height = (int) in.getHeight();
WritableImage out = new WritableImage(width, height);
for (int x = 0; x < width; x++)
for (int y = 0; y < height; y++) {
Color c = in.getPixelReader().getColor(x, y);
for (UnaryOperator<Color> f : pendingOperations) c = f.apply(c);
out.getPixelWriter().setColor(x, y, c);
}
return out;
}
 CAUTION
CAUTION
In real life, implementing lazy operations is quite a bit harder. Usually you have a mixture of operations, and not all of them can be applied lazily. See Exercises 12 and 13.
3.7. Parallelizing Operations
When expressing operations as functional interfaces, the caller gives up control over the processing details. As long as the operations are applied so that the correct result is achieved, the caller has nothing to complain about. In particular, the library can make use of concurrency. For example, in image processing we can split the image into multiple strips and process each strip separately.
Here is a simple way of carrying out an image transformation in parallel. This code operates on Color[][] arrays instead of Image objects because the JavaFX PixelWriter is not threadsafe.
public static Color[][] parallelTransform(Color[][] in, UnaryOperator<Color> f) {
int n = Runtime.getRuntime().availableProcessors();
int height = in.length;
int width = in[0].length;
Color[][] out = new Color[height][width];
try {
ExecutorService pool = Executors.newCachedThreadPool();
for (int i = 0; i < n; i++) {
int fromY = i * height / n;
int toY = (i + 1) * height / n;
pool.submit(() -> {
for (int x = 0; x < width; x++)
for (int y = fromY; y < toY; y++)
out[y][x] = f.apply(in[y][x]);
});
}
pool.shutdown();
pool.awaitTermination(1, TimeUnit.HOURS);
}
catch (InterruptedException ex) {
ex.printStackTrace();
}
return out;
}
This is, of course, just a proof of concept. Supporting image operations that combine multiple pixels would be a major challenge.
In general, when you are given an object of a functional interface and you need to invoke it many times, ask yourself whether you can take advantage of concurrency.
3.8. Dealing with Exceptions
When you write a method that accepts lambdas, you need to spend some thought on handling and reporting exceptions that may occur when the lambda expression is executed.
When an exception is thrown in a lambda expression, it is propagated to the caller. There is nothing special about executing lambda expressions, of course. They are simply method calls on some object that implements a functional interface. Often it is appropriate to let the expression bubble up to the caller.
Consider, for example:
public static void doInOrder(Runnable first, Runnable second) {
first.run();
second.run();
}
If first.run() throws an exception, then the doInOrder method is terminated, second is never run, and the caller gets to deal with the exception.
But now suppose we execute the tasks asynchronously.
public static void doInOrderAsync(Runnable first, Runnable second) {
Thread t = new Thread() {
public void run() {
first.run();
second.run();
}
};
t.start();
}
If first.run() throws an exception, the thread is terminated, and second is never run. However, the doInOrderAsync returns right away and does the work in a separate thread, so it is not possible to have the method rethrow the exception. In this situation, it is a good idea to supply a handler:
public static void doInOrderAsync(Runnable first, Runnable second,
Consumer<Throwable> handler) {
Thread t = new Thread() {
public void run() {
try {
first.run();
second.run();
} catch (Throwable t) {
handler.accept(t);
}
}
};
t.start();
}
Now suppose that first produces a result that is consumed by second. We can still use the handler.
public static <T> void doInOrderAsync(Supplier<T> first, Consumer<T> second,
Consumer<Throwable> handler) {
Thread t = new Thread() {
public void run() {
try {
T result = first.get();
second.accept(result);
} catch (Throwable t) {
handler.accept(t);
}
}
};
t.start();
}
Alternatively, we could make second a BiConsumer<T, Throwable> and have it deal with the exception from first—see Exercise 16.
It is often inconvenient that methods in functional interfaces don’t allow checked exceptions. Of course, your methods can accept functional interfaces whose methods allow checked exceptions, such as Callable<T> instead of Supplier<T>. A Callable<T> has a method that is declared as T call() throws Exception. If you want an equivalent for a Consumer or a Function, you have to create it yourself.
You sometimes see suggestions to “fix” this problem with a generic wrapper, like this:
public static <T> Supplier<T> unchecked(Callable<T> f) {
return () -> {
try {
return f.call();
}
catch (Exception e) {
throw new RuntimeException(e);
}
catch (Throwable t) {
throw t;
}
};
}
Then you can pass a
unchecked(() -> new String(Files.readAllBytes(
Paths.get("/etc/passwd")), StandardCharsets.UTF_8))
to a Supplier<String>, even though the readAllBytes method throws an IOException.
That is a solution, but not a complete fix. For example, this method cannot generate a Consumer<T> or a Function<T, U>. You would need to implement a variation of unchecked for each functional interface.
3.9. Lambdas and Generics
Generally, lambdas work well with generic types. You have seen a number of examples where we wrote generic mechanisms, such as the unchecked method of the preceding section. There are just a couple of issues to keep in mind.
One of the unhappy consequences of type erasure is that you cannot construct a generic array at runtime. For example, the toArray() method of Collection<T> and Stream<T> cannot call T[] result = new T[n]. Therefore, these methods return Object[] arrays. In the past, the solution was to provide a second method that accepts an array. That array was either filled or used to create a new one via reflection. For example, Collection<T> has a method toArray(T[] a). With lambdas, you have a new option, namely to pass the constructor. That is what you do with streams:
String[] result = words.toArray(String[]::new);
When you implement such a method, the constructor expression is an IntFunction<T[]>, since the size of the array is passed to the constructor. In your code, you call T[] result = constr.apply(n).
In this regard, lambdas help you overcome a limitation of generic types. Unfortunately, in another common situtation lambdas suffer from a different limitation. To understand the problem, recall the concept of type variance.
Suppose Employee is a subtype of Person. Is a List<Employee> a special case of a List<Person>? It seems that it should be. But actually, it would be unsound. Consider this code:
List<Employee> staff = ...;
List<Person> tenants = staff; // Not legal, but suppose it was
tenants.add(new Person("John Q. Public")); // Adds Person to staff!
Note that staff and tenants are references to the same list. To make this type error impossible, we must disallow the conversion from List<Employee> to List<Person>. We say that the type parameter T of List<T> is invariant.
If List was immutable, as it is in a functional programming language, then the problem would disappear, and one could have a covariant list. That is what is done in languages such as Scala. However, when generics were invented, Java had very few immutable generic classes, and the language designers instead embraced a different concept: use-site variance, or “wildcards.”
A method can decide to accept a List<? extends Person> if it only reads from the list. Then you can pass either a List<Person> or a List<Employee>. Or it can accept a List<? super Employee> if it only writes to the list. It is okay to write employees into aList<Person>, so you can pass such a list. In general, reading is covariant (subtypes are okay) and writing is contravariant (supertypes are okay). Use-site variance is just right for mutable data structures. It gives each service the choice which variance, if any, is appropriate.
However, for function types, use-site variance is a hassle. A function type is always contravariant in its arguments and covariant in its return value. For example, if you have a Function<Person, Employee>, you can safely pass it on to someone who needs a Function<Employee, Person>. They will only call it with employees, whereas your function can handle any person. They will expect the function to return a person, and you give them something even better.
In Java, when you declare a generic functional interface, you can’t specify that function arguments are always contravariant and return types always covariant. Instead, you have to repeat it for each use. For example, look at the javadoc for Stream<T>:
void forEach(Consumer<? super T> action)
Stream<T> filter(Predicate<? super T> predicate)
<R> Stream<R> map(Function<? super T, ? extends R> mapper)
The general rule is that you use super for argument types, extends for return types. That way, you can pass a Consumer<Object> to forEach on a Stream<String>. If it is willing to consume any object, surely it can consume strings.
But the wildcards are not always there. Look at
T reduce(T identity, BinaryOperator<T> accumulator)
Since T is the argument and return type of BinaryOperator, the type does not vary. In effect, the contravariance and covariance cancel each other out.
As the implementor of a method that accepts lambda expressions with generic types, you simply add ? super to any argument type that is not also a return type, and ? extends to any return type that is not also an argument type.
For example, consider the doInOrderAsync method of the preceding section. Instead of
public static <T> void doInOrderAsync(Supplier<T> first,
Consumer<T> second, Consumer<Throwable> handler)
it should be
public static <T> void doInOrderAsync(Supplier<? extends T> first,
Consumer<? super T> second, Consumer<? super Throwable> handler)
3.10. Monadic Operations
When you work with generic types, and with functions that yield values from these types, it is useful to supply methods that let you compose these functions—that is, carry out one after another. In this section, you will see a design pattern for providing such compositions.
Consider a generic type G<T> with one type parameter, such as List<T> (zero or more values of type T), Optional<T> (zero or one values of type T), or Future<T> (a value of type T that will be available in the future).
Also consider a function T -> U, or a Function<T, U> object.
It often makes sense to apply this function to a G<T> (that is, a List<T>, Optional<T>, Future<T>, and so on). How this works exactly depends on the nature of the generic type G. For example, applying a function f to a List with elements e1,..., en means creating a list with elementsf(e1),..., f(en).
Applying f to an Optional<T> containing v means creating an Optional<U> containing f(v). But if f is applied to an empty Optional<T> without a value, the result is an empty Optional<U>.
Applying f to a Future<T> simply means to apply it whenever it is available. The result is a Future<U>.
By tradition, this operation is usually called map. There is a map method for Stream and Optional. The CompletableFuture class that we will discuss in Chapter 6 has an operation that does just what map should do, but it is called thenApply. There is no map for a plainFuture<V>, but it is not hard to supply one (see Exercise 21).
So far, that is a fairly straightforward idea. It gets more complex when you look at functions T -> G<U> instead of functions T -> U. For example, consider getting the web page for a URL. Since it takes some time to fetch the page, that is a function URL -> Future<String>. Now suppose you have a Future<URL>, a URL that will arrive sometime. Clearly it makes sense to map the function to that Future. Wait for the URL to arrive, then feed it to the function and wait for the string to arrive. This operation has traditionally been called flatMap.
The name flatMap comes from sets. Suppose you have a “many-valued” function—a function computing a set of possible answers. And then you have another such function. How can you compose these functions? If f(x) is the set {y1,..., yn}, you apply g to each element, yielding {g(y1),...,g(yn)}. But each of the g(yi) is a set. You want to “flatten” the set of sets so that you get the set of all possible values of both functions.
There is a flatMap for Optional<T> as well. Given a function T -> Optional<U>, flatMap unwraps the value in the Optional and applies the function, except if either the source or target option was not present. It does exactly what the set-based flatMap would have done on sets with size 0 or 1.
Generally, when you design a type G<T> and a function T -> U, think whether it makes sense to define a map that yields a G<U>. Then, generalize to functions T -> G<U> and, if appropriate, provide flatMap.
![]() NOTE
NOTE
These operations are important in the theory of monads, but you don’t need to know the theory to understand map and flatMap. The concept of mapping a function is both straightforward and useful, and the point of this section is to make you aware of it.
Exercises
1. Enhance the lazy logging technique by providing conditional logging. A typical call would be logIf(Level.FINEST, () -> i == 10, () -> "a[10] = " + a[10]). Don’t evaluate the condition if the logger won’t log the message.
2. When you use a ReentrantLock, you are required to lock and unlock with the idiom
myLock.lock();
try {
some action
} finally {
myLock.unlock();
}
Provide a method withLock so that one can call
withLock(myLock, () -> { some action })
3. Java 1.4 added assertions to the language, with an assert keyword. Why were assertions not supplied as a library feature? Could they be implemented as a library feature in Java 8?
4. How many functional interfaces with Filter in their name can you find in the Java API? Which ones add value over Predicate<T>?
5. Here is a concrete example of a ColorTransformer. We want to put a frame around an image, like this:

First, implement a variant of the transform method of Section 3.3, “Choosing a Functional Interface,” on page 50, with a ColorTransformer instead of an UnaryOperator<Color>. Then call it with an appropriate lambda expression to put a 10 pixel gray frame replacing the pixels on the border of an image.
6. Complete the method
public static <T> Image transform(Image in, BiFunction<Color, T> f, T arg)
from Section 3.4, “Returning Functions,” on page 53.
7. Write a method that generates a Comparator<String> that can be normal or reversed, case-sensitive or case-insensitive, space-sensitive or space-insensitive, or any combination thereof. Your method should return a lambda expression.
8. Generalize Exercise 5 by writing a static method that yields a ColorTransformer that adds a frame of arbitrary thickness and color to an image.
9. Write a method lexicographicComparator(String... fieldNames) that yields a comparator that compares the given fields in the given order. For example, a lexicographicComparator("lastname", "firstname") takes two objects and, using reflection, gets the values of the lastname field. If they are different, return the difference, otherwise move on to the firstname field. If all fields match, return 0.
10. Why can’t one call
UnaryOperator op = Color::brighter;
Image finalImage = transform(image, op.compose(Color::grayscale));
Look carefully at the return type of the compose method of UnaryOperator<T>. Why is it not appropriate for the transform method? What does that say about the utility of structural and nominal types when it comes to function composition?
11. Implement static methods that can compose two ColorTransformer objects, and a static method that turns a UnaryOperator<Color> into a ColorTransformer that ignores the x- and y-coordinates. Then use these methods to add a gray frame to a brightened image. (See Exercise 5 for the gray frame.)
12. Enhance the LatentImage class in Section 3.6, “Laziness,” on page 56, so that it supports both UnaryOperator<Color> and ColorTransformer. Hint: Adapt the former to the latter.
13. Convolution filters such as blur or edge detection compute a pixel from neighboring pixels. To blur an image, replace each color value by the average of itself and its eight neighbors. For edge detection, replace each color value c with 4c – n – e – s – w, where the other colors are those of the pixel to the north, east, south, and west. Note that these cannot be implemented lazily, using the approach of Section 3.6, “Laziness,” on page 56, since they require the image from the previous stage (or at least the neighboring pixels) to have been computed. Enhance the lazy image processing to deal with these operations. Force computation of the previous stage when one of these operators is evaluated.
14. To deal with lazy evaluation on a per-pixel basis, change the transformers so that they are passed a PixelReader object from which they can read other pixels in the image. For example, (x, y, reader) -> reader.get(width - x, y) is a mirroring operation. The convolution filters from the preceding exercises can be easily implemented in terms of such a reader. The straightforward operations would simply have the form (x, y, reader) -> reader.get(x, y).grayscale(), and you can provide an adapter fromUnaryOperation<Color>. A PixelReader is at a particular level in the pipeline of operations. Keep a cache of recently read pixels at each level in the pipeline. If a reader is asked for a pixel, it looks in the cache (or in the original image at level 0); if that fails, it constructs a reader that asks the previous transform.
15. Combine the lazy evaluation of Section 3.6, “Laziness,” on page 56, with the parallel evaluation of Section 3.7, “Parallelizing Operations,” on page 57.
16. Implement the doInOrderAsync of Section 3.8, “Dealing with Exceptions,” on page 58, where the second parameter is a BiConsumer<T, Throwable>. Provide a plausible use case. Do you still need the third parameter?
17. Implement a doInParallelAsync(Runnable first, Runnable second, Consumer<Throwable>) method that executes first and second in parallel, calling the handler if either method throws an exception.
18. Implement a version of the unchecked method in Section 3.8, “Dealing with Exceptions,” on page 58, that generates a Function<T, U> from a lambda that throws checked exceptions. Note that you will need to find or provide a functional interface whose abstract method throws arbitrary exceptions.
19. Look at the Stream<T> method <U> U reduce(U identity, BiFunction<U,? super T,U> accumulator, BinaryOperator<U> combiner). Should U be declared as ? super U in the first type argument to BiFunction? Why or why not?
20. Supply a static method <T, U> List<U> map(List<T>, Function<T, U>).
21. Supply a static method <T, U> Future<U> map(Future<T>, Function<T, U>). Return an object of an anonymous class that implements all methods of the Future interface. In the get methods, invoke the function.
22. Is there a flatMap operation for CompletableFuture? If so, what is it?
23. Define a map operation for a class Pair<T> that represents a pair of objects of type T.
24. Can you define a flatMap method for Pair<T>? If so, what is it? If not, why not?