How to Use Objects: Code and Concepts (2016)

Part II: Contracts

Chapter 4. Contracts for Objects

One of the most vital questions in every programmer’s life is: Does this code work? If it turns out that the code does not work properly, you’re in for lengthy debugging sessions, the team will get irritated with their stalled progress, the boss will complain about ever-increasing backlogs, and customers will become frustrated with the reliability of the product. So how can you convince yourself, your team, your boss, and finally your customers that the code you write does work? And more importantly, how can you be confident that it does not just pass your test cases today, but will keep working tomorrow?

The fundamental problem in this area is that it is not obvious what good arguments for “this code works” really look like. Showing that the code is broken can be done by a single test case with an unexpected result, but how can you argue that your code will pass any test case or use case that your team, your boss, or your customers will come up with? In fact, the problem is so non-obvious that computer science has been struggling with it ever since its infancy: starting with the seminal papers by Floyd and⁹⁰^,¹¹⁹ Hoare in the late 1960s, through a surge of foundational computer-checked¹¹⁰^,¹²¹^,²⁵⁴^,²⁵³ formal proofs in the 1990s, basic studies of heap-manipulating programs in²¹³^,⁴⁹^,¹⁷⁶^,²⁴⁶^,¹⁰²^,¹⁰³ the early 2000s, scalable implementations and the solving of some intricate²²^,¹²^,⁷⁹^,¹⁶⁸^,³⁶ subproblems in the late 2000s, and industrial applications around and after¹⁸⁸^,¹⁶⁷^,¹³⁴^,²³⁰ 2010. Judging from these latest breakthroughs on verifying core components⁶⁶^,⁶⁷^,¹⁵³^,¹³⁸ of operating systems, we seem to be in the happy situation that the problem of arguing about the correctness of programs has been understood in all relevant facets.

What does all of this mean to practitioners? Depending on their general levels of politeness and honesty, they may call the above work “impressive,” “intimidating,” “irrelevant,” or “formal rubbish.” By comparison, Meyer’s notion of design-by-contract has inspired software engineers and¹⁸²^,¹⁸¹ has found its way into everyday jargon: Mailing lists and bug trackers discuss “contracts” and “broken invariants” as a matter of course, and even books on object design naturally cover contracts of methods. In the form²⁶³ of the Java Modeling Language (JML), design-by-contract even progresses¹⁴⁹^,¹⁵¹^,¹⁵⁰^,⁵⁶ beyond practical tool support to formal reasoning.

The purpose of this and the following chapters is to provide a practical, self-contained, and understandable view on the question of correctness, always starting from the goal of “making the code work.” From the huge amount of work sketched out previously, we will pick those concepts and arguments that do crop up in practical coding, in team meetings, and on mailing lists. Then, we will explain and connect them to create a solid conceptual framework for arguing about whether and why code works.

The material presented has one immediate benefit: Many of the lengthy and more intricate discussions from Part I can now be compressed in a few^1.8.1^1.8.2^4.1 sentences: The central point of encapsulation is made precise by contracts^2.1.3 and model fields. The question of when subjects fire change notifications^4.1^4.2.3 in the OBSERVER pattern is clear from the idea of class invariants. The^3.1.1 Liskov Substitution Principle and behavioral subtyping are contained in the idea of contract inheritance. The new view will therefore make your team’s⁵⁴communication more effective, if nothing else. Given that communication has long been recognized as a major bottleneck of software development, the knowledge and understanding of contracts will boost productivity.

As a further point of motivation, you may be surprised to learn that practitioners actually follow the guidelines presented subsequently, especially when things get complicated. Indeed, when preparing the running example for Section 4.1, we found the following comment at the head ofGapTextStore.arrayCopy():

A length < 0 cannot happen → don’t hide coding errors by checking for negative lengths.

The statement “length ≥ 0” is an “assertion,” as introduced later in this chapter, and obviously the developers assumed it would always hold, so that they can simplify their code. In fact, the goal not to “hide coding errors” refers forward to the “non-redundancy principle” in Section 4.5: The method just goes ahead and accepts that maybe an exception is thrown to alert the caller to a mistake.

In the presentation, we will omit all formal details and definitions, but we will never lie or cheat. If after following and applying the material of this chapter you have become keen to know more about the formal questions behind it, you can read up and fit in those parts that we have left out. You will not have to rearrange or even unlearn ideas. The presentation merely takes a few “skips” beyond details that are formally relevant, but “obvious” to the practitioner. The final section of this chapter, Section 4.7, gives you a taste of these additional details, just as an appetizer.

4.1 The Core: Assertions Plus Encapsulation

This core section, according to its purpose in the book, faces the daunting task of giving a guided tour of 50 years of computer science research in a few pages, while translating formal arguments into everyday insights. We solve this by introducing only the core concepts and their connections, while deferring discussions to the subsequent sections. Also, to avoid a formalistic style and to maintain the idea of a guided tour, we present the material in the form of a continuous narrative, in which we relive the discoveries of others in a running example.

Development practice knows many ways of arguing about whether some piece of code works: write a test case, start the debugger, execute the code mentally, compare it to code seen elsewhere, say that it combines a few well-tested steps in an obvious manner, and many more. However, none of these methods works all the time or is even practical for every piece of code: You cannot possibly understand a program of 50,000 lines by tracing it with the debugger, nor can you imitate or combine existing solutions in all situations.

To arrive at a solid framework for reasoning about code, let us assume that we have to convince a colleague—perhaps you even know such a person—who does not believe a single thing you say, except when confronted with really undeniable facts. We will start our quest by anticipating that nasty colleague’s questions and will devise unimpeachable answers.

As a running example, we look again at Eclipse’s GapTextStore, which^1.3.1 we considered earlier in the section on an object’s data structures. To recap, a GapTextStore supports the modifications of text required by editors efficiently. For space-efficiency, the data is kept in a flat array of characters. For efficient modifications, that array contains a “gap,” which does not contain actual data but is left open to receive additions and removals (see the following diagram, which replicates Fig. 1.2). For a modification, the gap is moved to the editing location, then the gap start is adapted to insert or delete characters. The main trick is that editing is a local activity, and moving the gap touches only the characters between the old location and the new location.

Become wary about what you think you know about your code.

The purpose of our “conversational” approach to correctness is that it suggests a certain attitude toward code: To write correct code, it is necessary to start questioning the assumptions you are making and to argue that they do hold true. You will certainly have found yourself thinking about questions like the following: Why is this particular variable non-null? Why is that number always greater than 0? Why is this collection always non-empty? You will also have discovered, in debugging sessions, some such questions that you had not thought about. A main contribution of the conceptual framework established by computer science is that it leads up to finding all relevant questions systematically.

Suppose, then, that you have written the class GapTextStore and your disbelieving colleague has to use it. He comes up with a JUnit test case^5.4.9 and is annoyed to find that the object does meet his expectations (set initializes the gap store, replace combines a deletion with an insertion):

gapstore.GapTextStoreTest.inserting

1 store = new GapTextStore();
2 store.set("Hello, world");
3 store.replace(7, 0, "wonderful ");
4 String res = store.get(0, store.getLength());
5 assertEquals("Hello, wonderful world", res);

However, he wants to know whether he can rely on this behavior. You explain patiently what your class does. You may first say, in the manner of mental execution:

The gap store really just maintains a string. So when you place “Hello, world” into the store in line 2, that string becomes the store’s entire content. Unlike usual strings, you can modify the store: In line 3, you splice in “wonderful” at character position 7 (deleting 0 characters)—let’s see—just before the “w”. Naturally, you get “Hello, wonderful world.” What is it you do not understand?

But, of course, your colleague really wanted to know whether this works in general, as shown in the following test. Also, he wanted to know how the thing works, not just the result.

gapstore.GapTextStoreTest.insertGeneral

1 store = new GapTextStore();
2 store.set(initial);
3 store.replace(pos, 0, insert);
4 String res = store.get(0, store.getLength());
5 String expectedResult = initial.substring(0, pos) + insert
6 + initial.substring(pos);
7 assertEquals(expectedResult,res);

Now the argument becomes a bit more involved, since you have to talk about arbitrary texts and positions, and you also have to connect the explanation to your data structures. So, drawing Fig. 4.1 on the whiteboard, you continue:¹

1. If you are of a disbelieving disposition yourself, which is good for a dependable developer, you may start looking at the original code now. You will find that several points in the subsequent presentation are slightly simplified. Even so, the omitted details do not invalidate our arguments.

The nifty idea of the gap store is that it keeps the text in an array, but always leaves a “gap” into which new text can be inserted efficiently. Initially, after line 1, the gap fills the entire array. When storing the initial string in line 2, its characters are written to the beginning of the gap. So you see that the current content, as seen from the outside, is the array except for the shaded gap area. Line 3 now shows the heart of the gap store: Whenever a modification takes place, the gap is moved to the desired position, in this case pos. In this way, the new characters of insert can be placed into the gap, as I said before.

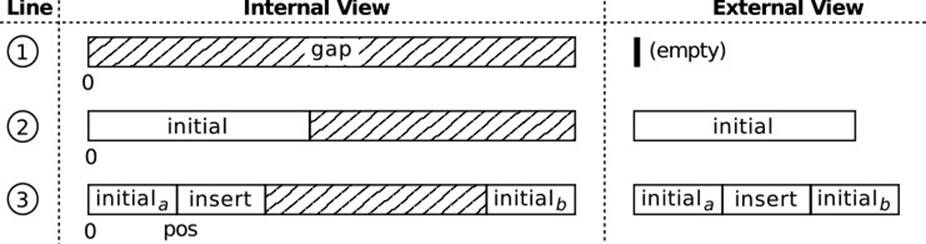
Figure 4.1 Tracing an Argument About GapTextStore

Your colleague now seems satisfied that you know what you are doing. He resolves to look at the code some more, but soon gets giddy with all the indices he finds there. So he comes back asking:

Do I really have to know about those details you explained?

Having read Chapter 1, your answer is, of course:

No, all of those are encapsulated. You need to understand only the external view.

At this point, let us leave the fictional conversation for the moment and consider which arguments have been used.

Contracts establish a consistent external view on an object’s behavior.

The key point that we will pursue is that contracts save time and effort in^1.1 software construction, because they enable developers to work with objects that they have not created themselves and do not understand in detail. For this to work out, the objects must be written to allow for consistent arguments using the external view only.^11.5.1

Let us then continue the explanation of GapTextStore. We must find an external view for the internal steps in Fig. 4.1, such that the external view remains in lockstep with the internal one. To explain the connection, we might say to the colleague, “So you see that the current content, as seen from the outside, is the array except for the shaded gap area.” To be able to continue in a precise manner, let us add the actual field names to the internal view, as shown in Fig. 4.2. Since the external view is “really just a string,” we describe that string by giving some of its properties inFig. 4.3 [using notation a[i..j] to denote the array slice from i (inclusive) to j (exclusive)]: The content consists of the non-gap parts of the array fContent, the length is just the number of characters in those parts, and a single character can be picked by case distinction. You should convince yourself that the overview is correct by comparing these descriptions with Figs. 4.2 and 4.1.

Figure 4.2 Data Structure of a GapTextStore Object

Figure 4.3 External and Internal Views of the GapTextStore

The external and internal views given in this way really offer different perspectives on the object’s state. The internal one is phrased in terms of the object’s actual fields, while the external one cannot be cast in these terms, because we wish to hide these internals.

Model fields present an external view onto an object’s state.

¹⁵⁵^,¹⁵⁴^,⁶²^,¹⁸⁸^4.2.1Model fields are a description of the object’s state that does not give away the internals and conforms to the clients’ understanding of the object’s purpose. To find suitable model fields, just observe the terms you use to describe the object to someone else: You want the person to understand the object, so you invent summary “data” that explains the object’s state closely enough.

Model fields are therefore essential for achieving encapsulation: They enable us to argue about an object’s state without disclosing its actual fields and data structures. Without them, it would not be useful to hide an object’s internals through language-level mechanisms, because a client would have to know them anyway. Model fields enable us to ban an object’s^1.1 technical details from our discussions entirely and to create truly black-box objects.

^1.3.3The object’s properties (i.e., those fields with getters and setters) are special: They are publicly visible through the accessors, so they are model fields; at the same time, they correspond one-to-one to implementation fields. In the gap store example, we could, for instance, formulate the postcondition of getLength() as follows (\return is the return value, as would be expected; the backslash serves as an escape symbol to identify JML keywords):

Assertions describe snapshots of the program’s state during execution.

Now that we can talk safely about an object’s state, what do we say? Looking back at the argument, and in particular Fig. 4.3, it would seem that a good strategy is to point at specific lines in the code and to describe what the object, or the program’s state in general, looks like at that point. This is, indeed, the fundamental idea behind software verification, as introduced by Hoare in 1969: An assertion is a statement about the program’s state¹¹⁹ that holds at a particular point in the code whenever that point is reached during execution. For our purposes, the assertion can be formulated in precise English or pseudo-code Boolean expressions, but the approach can be refined to allow formulas as assertions and mathematical proofs to verify that they always hold (see Section 4.7 for a glimpse at this).

Let us clarify this at the example. The previous lengthy explanation mentioning the different line numbers can be transformed into an assertion-style explanation by putting the assertions into comments. In line 2, we know that the gap store is empty; lines 4 and 6 trace the intermediate steps as before; line 9 captures the final outcome that we have derived by reasoning. Lines 10–12 then test our expectation: We recompute the^5.1 expected result on strings, without using the gap store, and then compare it to the actual result using assertEquals from JUnit. That test will throw^1.5.4^4.5 an exception if the expectation is violated.

gapstore.GapTextStoreTest.insertGeneral

1 store = new GapTextStore();
2 // store.content = ""
3 store.set(initial);
4 // store.content = initial
5 store.replace(pos, 0, insert);
6 // store.content = initial.substring(0,pos) + insert
7 + initial.substring(pos)
8 String res = store.get(0, store.getLength());
9 // res = store.content
10 String expectedResult = initial.substring(0, pos) + insert
11 + initial.substring(pos);
12 assertEquals(expectedResult,res);

One question that often arises on the first encounter with assertions is whether they include types. A purist would say that the type of some data item or object must, of course, be talked about when considering software correctness, because the type influences the behavior. The practitioner will, however, not bother with stating the obvious. In the following declarations, both length and history have declared types that match the types of their runtime content exactly. It would be redundant to point this out in an assertion. For purchases, one knows more about the actual object than is given by the type, and one might state an assertion purchases instanceof ArrayList.

private int length;
private ArrayList<Integer> history = new ArrayList<Integer>();
private List<ProductOrder> purchases =
new ArrayList<ProductOrder>();

^3.1.9In particular, assertions about types are necessary to argue that a downcast will not fail.^4.7.3 A typical situation is shown by the following if statement, where the test yields just the additional knowledge that guarantees the success of the downcast:

if (obj instanceof Integer) {
Integer value = (Integer)obj;
... work with value
}

We would therefore propose to include type information into assertions only if the static and dynamic types differ and if that difference ever becomes important for the correctness arguments.

Assertions are conceptual breakpoints.

From a practical perspective, assertions can be understood as breakpoints that you set mentally inside the code. Each imaginary “stop” at an assertion would check whether the statement you have made is actually true.

Although we can now write down what we think we know about our program, we cannot yet argue that it actually does hold. In particular, we will have to describe what each method call in the test does to the gap store’s state.

Contracts capture the behavior of objects.

The description of an object’s state through model fields must be complemented by descriptions of its methods to answer this question: How do¹⁸² method calls modify the object’s state? The crucial point of design-by-contract is that this goal is best accomplished by associating with each method a pair of special assertions:

• The pre-condition must hold at the beginning of the method, after the parameters have been set and just before the body starts executing.

• The post-condition must hold at the end of the method, after the return value (if any) has been computed and just before execution returns to the caller.

The post-condition may refer to the current state as usual and additionally¹⁵¹ to the pre-state, where the pre-condition holds, via \old (again using the backslash as an escape symbol). Also, it can access the return value as \return.

If assertions are like breakpoints, then pre- and post-conditions are like function breakpoints (Fig. 4.4): They are hit whenever execution enters or leaves a method, and at those points you can examine and describe the state.

Figure 4.4 Illustration of a Method’s Contract

The pre- and post-conditions together are also called the method’s contract. The contracts of all methods together are the class’s contract.

Let us try this idea immediately on the example. The main method is replace(pos,del,ins). The API documentation says that it “replaces the specified character range with the given text.” The pre-condition states what must hold when the method starts executing. Here, the “character range” must be within the existing content; otherwise, the deletion operation does not make sense. In the form of a Boolean expression:

The post-condition states what the method achieves, or what it leaves behind for the caller to work with. In the example, the replacement acts on the content of the gap store. The post-condition of replace then specifies the new content:

content =\old(content.substring(0, pos))+

\old(ins) + \old(content.substring(pos + del))

We have to use pre-state \old(ins), because in principle the method may have modified the parameter during execution. A post-condition that is stated in terms of the initial values of the parameters then gives a direct functional dependency from the outcome on the input—just as one would expect for a function-like construct such as a method.

With this new knowledge, we can actually deduce that the assertion in line 12 of the example holds, assuming that the assertion in line 4 holds and pos is within initial. This, in turn, can be derived from the post-condition of set(text). That method, according to the API, “replace[s] the content of the text store with the given text.” Its pre-condition is true (i.e., it can always be called with any text as a parameter), and its post-condition is

content = \old(text)

Great! So the assertion in line 4 also holds by deduction, and this time without checking anything else.

The theme of pre- and post-conditions has actually been explored in the literature in many different contexts and from many different perspectives. Let us briefly look at these definitions, because each new perspective offers a fresh angle for comprehension. Also, it connects your understanding to that of colleagues you might be talking to.

If the pre-condition holds when the method is called, the post-condition must hold when it finishes.

This view makes explicit a central logical dependency: Since we assume that the pre-condition holds at each method call, the method’s body can work under the assumption that it holds regardless of the actual call site—it is possible to deduce the method’s post-condition once and for all.

Garbage in, garbage out.

This is a popular negation of the previous view: If the pre-condition does not hold, we will not know anything about the post-condition—it might or might not hold, and the result can even be arbitrary “garbage.”

The slogan’s sloppy formulation also clarifies in an intuitive way that a method’s developer cannot be blamed if the method is used outside its contract. For instance, if the skeptical colleague demands that “Appending should work in my test case!” you can simply reply by saying, “Garbage in, garbage out.”

gapstore.GapTextStoreTest.insertTooFarRight

store.set("Hello, world");
store.replace(13, 0, "!");

The caller is responsible for ensuring the method’s pre-condition, and the method is responsible for ensuring its post-condition under the assumption that the pre-condition holds.

Clearly, if the pre-condition is to hold before the method starts, then only the caller can provide the necessary argument. Conversely, only the method can argue that the post-condition holds based on the knowledge of its internal algorithm.

¹⁸²This view is, in fact, Meyer’s original proposal, which has made contracts^1.4.3 popular with a wider community: It points out the link of methods as service providers to real-world service providers. For instance, to buy a pizza from a delivery service, you have to choose a pizza that is on the menu, state your address clearly and correctly, and pay the bill to the driver. This is the pre-condition for using the service. Once it is established, the driver hands over the pizza in a moderately hot state; the post-condition is “you have got the pizza you ordered.” In software engineering, the formulation divides the responsibility for the proper working of the code fairly between the developer of a method and the developer invoking the method.

Despite its widespread use in the literature, this original formulation still does not quite link to everyday arguments used by developers. We would offer the following alternative:

The pre-condition states when the method may be legally called; the postcondition states what it achieves.

This very high-level view explains contracts in terms of the method’s purpose and also relates to the immediate questions of the caller: Can I call the method? And if so, what do I gain by calling it? The first is, of course, the same as asking for the caller’s responsibility; the second rephrases the method’s responsibility from an after-the-fact perspective: What has the method done for me when it finishes?

In summary, we have seen how the working of methods can be described and specified based on assertions, which capture the program state at specific points. In particular, we have seen that pre- and post-conditions act as contracts between caller and callee, and that they enable the caller to reason about an object’s behavior without knowing its internal details.

Contracts alone are insufficient for detailed reasoning.

We have not, however, discussed sufficiently how the method’s developer can argue that he can guarantee the post-condition after execution. The central open question is this: When the method starts executing, how can the developer know that the object’s internal fields are in proper working order? The model fields cover only the externally visible aspects—not the internal data structures.

For instance, the following method extracts a range of text into a string. How do we know that the case distinctions in lines 2 and 5 make sense? Can we be sure that fContent is not null, so that lines 3, 6, and 8–9 run through without a NullPointerException?

org.eclipse.jface.text.GapTextStore

1 public String get(int offset, int length) {
2 if (fGapStart <= offset)
3 return new String(fContent, offset + gapSize(), length);
4 int end = offset + length;
5 if (end <= fGapStart)
6 return new String(fContent, offset, length);
7 StringBuffer buf = new StringBuffer(length);
8 buf.append(fContent, offset, fGapStart - offset);
9 buf.append(fContent, fGapEnd, end - fGapStart);
10 return buf.toString();
11 }

To keep track of such internals, we have to complement the pre-condition by a statement about the object’s fields. This assertion is called the class invariant.

Class invariants capture the consistency of objects.

So what does the method get have to know about the this object? Certainly that fContent is not null and that fGapStart and fGapEnd lie within that array, since otherwise lines 3, 6, and 8–9 will yield invalid character ranges—that is, character ranges that are not allowed by the preconditions of the String constructor and append, respectively. An object is “consistent” if it meets these basic criteria, if the statement you rely on holds “at all times” (well, almost, as we shall see). Incidentally, the term “invariant” relates precisely to this idea of not changing, of being invariably true. But where does this reasoning take us?

The invariant captures the intuitive understanding of a “proper object.”

The reasoning takes us precisely to Fig. 4.2, which really just depicts a “normal” gap store’s internal state. Let us repeat the figure here for convenience:

Of course, a picture is rather imprecise and open to interpretation. Fortunately, we can also write the invariant down as an assertion based on the picture—it should not be a great surprise that it is really what we have written up in English before:

fContent ≠ null && 0 ≤ fGapStart ≤ fGapEnd ≤ fContent.length

The code of get makes sense if you relate it to these insights: Lines 2–6 treat the special cases in which the requested range is entirely to the left or to the right of the gap, and lines 7–9 treat ranges overlapping the gap.

You are already working with invariants all the time.

Invariants are not mysterious or incomprehensible. All experienced developers have a very good idea of the internal structure of their objects—otherwise, they would never get their code to run. The following, more everyday views on “invariants” might help you link the terminology to your own style of argumentation—whenever you find yourself thinking along these lines, start to formulate an invariant that is as precise as possible, in whatever form you find suitable and are comfortable with.

• My object internally looks like this.

• The object is OK now.

• The object is usable.

• Of course, I always know that ...

• This field cannot contain / always contains ...

• This should not be the case!

• This field is always greater than that field.

Fig. 4.5 depicts another useful intuition that might link to your development experience. While you “work with an object,” you somehow “open up” the object, or you penetrate its encapsulation boundary, to get to the object’s^1.1 internals. When you are done, you “close” the object, at which point it becomes “whole” again. This intuition has the further attraction that it^4.4 can be grounded in a solid formalization.²¹

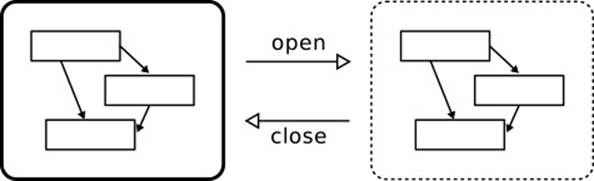
Figure 4.5 Intuition of Class Invariants

Writing down or drawing the invariant is, of course, an effort, but one that is certainly worthwhile: You can leave a note, to yourself or to others, of how an object’s fields are interrelated and what their individual purposes are.

There is one question about invariants that has led to some controversy: When does that assertion actually hold? The term “invariant” itself suggests that it is true all the time, but this is, of course, nonsensical: The gap store’s code will at some point allocate the array fContent, but will set fGapStart and fGapEnd only a few statements later; or it proceeds the other way around. For the duration of those few statements, then, the invariant does not hold—the diagram is “broken.” So when does the invariant hold?

Over the years, many methodologies have been proposed to delineate^4.4 precisely those times at which the class invariant must be shown to hold. Rather than follow these historical detours, let us start with a single general statement that comprises them all:

The class invariant holds for every instance whenever no code of the class runs.

This statement is so general that it might be hard to comprehend at first. Let us start from a practical perspective. As a developer, you will know that feeling of unease when working for a short time “against” the diagram of a “proper object” you have in your mind. Subconsciously, you start tracking what needs to be done to “repair” the object. When you have the diagram on paper, you will be retargeting references, moving index pointers, and so on. The point is always this: When your current code finishes working and your class yields control to something else, then the object must again be “in good shape.” In other words, the invariant may be broken only as long as your own class is in control, as long as its code keeps running and can repair any damages before someone notices.

Another way of looking at the situation is by analogy. You will have seen the following label attached to critical doors in public buildings. Of course, “at all times” implicitly includes the qualification “except when someone is operating the door to pass through.”

It is worth looking at other definitions, because they characterize special and common situations, even if they do not tell the whole story. Perhaps the most popular characterization of when the class invariant must hold is¹⁸¹ this one:

Every public method can assume the invariant at the start and must establish it in the end.

The relation to our own formulation is clear: Whenever execution enters a public method, it potentially has come from the outside, so the invariant does hold. Whenever a public method returns, it potentially leaves the class’s code, so the method should better leave the object intact. This guideline is very useful, as it establishes a warning bell inside the developers’ minds: Before leaving the public method, the object must be put “in order.”

Another benefit of this formulation is the clear link to an object’s life cycle (Fig. 4.6). Throughout the life cycle, methods get called and return. At each entry, they assume that the invariant holds and they keep it intact when they finish execution. In this way, the next method call can always assume the invariant does, indeed, hold.

Figure 4.6 Invariants and Public Methods

Class invariants do not belong to the class’s contract.

Finally, we wish to make explicit that although invariants belong to the conceptual framework of design-by-contract, they do not belong to a class’s¹⁸² contract (which is the collection of all method contracts) since they deal solely with the internal view of the object. If anything, they are a contract of the class’s developers with themselves (Fig. 4.6): They promise to themselves to keep the object in good shape, for the next time that a method should be invoked and the object’s machinery kicks in.

Public invariants relate the model fields from a client’s perspective.

There is, however, a second kind of invariant that does belong to the class’s¹⁵¹^(§3.3) contract: public invariants (or type invariants), which describe consistency conditions on the client-visible, published state of an object. For instance, the model fields of a gap store in Fig. 4.3 obey the following constraint:

length = content.length

This published constraint then allows us to argue about the following method appendGeneral(), which is supposed to add the given string to the end of the gap store. The post-condition (4.1) of getLength() is phrased in terms of the model field length, while the pre-condition (4.2) of replace uses content.length instead, because this is more natural for a method modifying content. Without the public invariant, we could not deduce that the call to replace is legal.

public void appendGeneral(String txt) {
store.replace(store.getLength(), 0, txt);
}

4.2 Elaborating the Concepts by Example

The previous section has introduced the core concepts of design-by-contract and of mainstream correctness arguments about code. The remainder of this chapter is dedicated to increasing the level of detail and to exploring some of the implications and ramifications of those concepts.

Despite its relative simplicity, the example of GapTextStore is too complex for this purpose. We therefore discuss a special iterator over an array instead. The task of the ThresholdArrayIterator is simple: Implement the Iterator interface for walking an array of ints, but return only elements that are no greater than a given threshold.

The code is brief and straightforward (Fig. 4.7). The general idea is that a is the input array, threshold is the given threshold, and i is somehow the current index. The constructor initializes everything, then hasNext() and next() behave as specified in the Iterator interface. The main work happens in findNext(), which advances i and checks elements against the threshold on the way. But how do we know that the code works?

public class ThresholdArrayIterator implements Iterator<Integer> {
private int a[];
private int i;
private int threshold;
public ThresholdArrayIterator(int [] a, int threshold) {
// avoid side effects from outside
this.a = Arrays.copyOf(a, a.length); this.i = 0;
this.threshold = threshold;
findNext();
}
public boolean hasNext() {
return i != a.length;
}
public Integer next() {
Integer tmp = a[i];
i++;
findNext();
return tmp;
}
private void findNext() {
while (i != a.length) {
if (a[i] <= threshold)
break;
else
i++;
}
}
public void remove() {
throw new UnsupportedOperationException();
}
}

Figure 4.7 An Iterator over Arrays

This section analyzes the necessary reasoning in detail. Before we proceed, here is a sketch of the overall contract we are aiming for. Since the iterator works on a sequence of elements, we capture an external view on its state by two model fields seq and pos. The field seq contains the elements returned by the next() method. It is an array, so that seq.length gives its length. The second model field pos is the iterator’s current position within seq. Using these model fields, the contract of hasNext() is straightforward: It can be called at any time and checks whether the iterator has reached the end of the sequence.

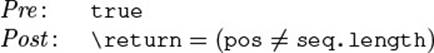
The contract of next() also captures the intuitive 'margin-bottom:0cm;margin-bottom:.0001pt; text-align:center;line-height:normal'>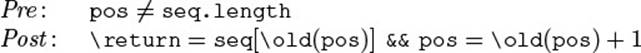

This overview leaves many points to be considered: What exactly are the elements of seq in the case of a ThresholdArrayIterator? How are the model fields related to the object’s concrete fields? What is the purpose of the constructor? And how are the public contracts related to the methods’ actual code? These and many more questions will be explored now, including the question of how we have arrived at the these contracts.

4.2.1 Invariants and Model Fields

We start by capturing the general setup of the class. The developer has, unfortunately, blundered a bit on the naming in the example class: i as^1.2.3 a field name is too short and too generic to convey its meaning and purpose. It appears to be an index into the array a, but which one exactly? Furthermore, we need to state precisely which elements the iterator returns without looking into its internals. Both questions are relevant to understanding the class: The first question relates to the internal class invariant,^4.1 the second to its external state description by model fields. As we shall see, the two are intertwined, because they are just two perspectives on the same thing: the object’s state. Let us start with the class invariant: What does the developer know about an iterator object? Fig. 4.8 captures the essence (note that the class invariant is private and can therefore access the object’s^4.1 internals):

The index i references the next element to be returned by next().

Figure 4.8 Invariant of the ThresholdArrayIterator

This idea is supported by the code of next(), which just returns the element at index i. The traversal by findNext() will skip elements that are greater than the given threshold. This reasoning suggests that field i should be renamed to nextElement. As we will see later, it would be even better to call it currentElement, because it is the element that the iterator is currently positioned at.

The earlier statement about i is certainly understandable to developers, but it is not a proper assertion, and therefore not a proper class invariant. Specifically, the meaning of “next” points to some future action, while assertions can talk about only the current state at the point when they are encountered.

Find formulations for assertions that talk about only the current state.

This restriction on assertions is perhaps the biggest challenge when first applying design-by-contract: Developers are so used to talking about the past and future execution of their program that they usually feel constrained when they can talk about only the present. The mental exercise to be practiced is this: Do execute the program in your head, but when you look at an assertion, detach yourself from the execution, interrupt the mental debugger, and talk about only what you know right now. Practicing this ability is really worthwhile. Indeed, once you get the knack of it, all those longish explanations about why and when you got to the current point in the execution can be cleared away. Your team’s discussions will become much more focused and more precise.

Another motivation for practicing this mindset is its connection to the^1.4.1^1.1^11.1 fundamentally object-oriented perception of objects as entities that communicate by sending messages to each other: When an object receives a message, it reacts appropriately, but one disregards the sender or the sequence of messages. One thinks about the reception of a message and the subsequent reaction as an isolated occurrence, up to the point where messages are^8.4 sent asynchronously, and the delivery occurs at some undetermined later point in time.

To get back to the example, the point “now” for class invariants is really any point where no code of the class runs. How can we get rid of the term “next,” with its implicit reference to a later call to next()? The essential insight here is that the “next element” really relates to the outsideview, so that it cannot be captured by internal considerations alone. We first have to introduce suitable model fields.

Model fields provide a strong handle on the class’s purpose.

From the clients’ perspective, the iterator is always a specific position pos within the imaginary sequence seq formed by those elements from a that are no greater than threshold. As with usual arrays, the iterator can also be at position seq.length, indicating that the sequence has been exhausted. So we have already identified the model fields: seq and pos.

To relate them to the internals, we have to talk about “those elements in a up to some index j (exclusive) that are no greater than threshold.” Since this phrase is rather unwieldy, let us introduce the notation a_≤[. . . j] for the (imaginary) array containing these elements. Then, we can define the model fields precisely: seq encompasses all such elements—it spans the entire array; pos is the number of such elements that have already been traversed.

With these definitions, we have achieved the goal of eliminating the term “next” from the proposed invariant, by giving the meaning of i in the definition of pos: i is given as the representation of the element in the result sequence that the iterator is currently pointing to. Even the special case pos = seq.length is included in the representation as i = a.length.

Invariants usually include safety conditions.

For this scheme to work properly, however, we must make sure that i never stops at an element that is greater than the threshold; otherwise, the same position pos would be represented by different values of i. The term “never” indicates a consistency condition on the object, so we formulate the following class invariant. We also note in passing that, as a safety condition, i never leaves a (except at the one-past-the-end position).

It is interesting to note that this invariant is really just what a developer would answer, after some thought, to the following questions by a disbelieving colleague: “What do you mean by ‘i never leaves a’?” “Are you sure that next() will always return an element no greater thanthreshold?” “How do you know when you have hit the end?”

Model fields capture the abstraction implemented by the class.

Note that both model fields are wholly imaginary. In fact, defining the^1.1^1.4.3^1.8.2 model fields well is a big step toward giving a useful outside view on the object, and therefore toward defining a useful API. In essence, we have postulated in the beginning that the clients’ view should dominate an object’s purpose and definition, and model fields are one essential ingredient to that view, since they capture the central aspects of the object’s state.

4.2.2 Contracts in Terms of Model Fields

If the model fields capture a client’s view on the object’s state, then the method contracts capture the client’s view of its behavior. The example has only two public methods that need to be described: next() and hasNext(). We will now discuss their contracts in some detail.

Phrase contracts in terms of public knowledge and model fields.

The purpose of contracts is to inform clients about what methods expect and what they guarantee in return. A necessary prerequisite is, of course,¹⁸¹ that clients can understand the contracts. Meyer calls this requirement the pre-condition availability principle: Contracts must not refer to the class’s internals, but only to publicly available information such as model fields and public invariants.

Let us start with the simpler method hasNext(), which does not modify the iterator’s state. Here is the code again for convenience:

thresholditer.ThresholdArrayIterator

public boolean hasNext() {
return i != a.length;
}

The pre-condition states under which circumstance the method may be called. According to the interface Iterator, clients may call the method at any time, so the pre-condition is true. The post-condition just describes the outcome of the test, but we cannot simply write

\return = (i ≠ a.length)

because that would refer to the class’s internals that the caller does not understand. Fortunately, i is closely related to the model field pos by (4.4), so that i = a.length is just the same as pos = seq.length, given that the invariant (4.5) forbids that i ever stops at an element not in the output sequence. All in all, we can simply state the post-condition of hasNext() as

Again, let us relate this to the API documentation, which says: “Returns true if the iteration has no more elements.” Our check (4.6) expresses just this condition: The imaginary current result position still points to some element in the imaginary result sequence.

A contract must make sense from the method’s purpose.

So far, we have used a syntactic meaning of “understanding”: All fields mentioned in contracts must be public. However, “understanding” should also encompass the deeper meaning of “insight”: When a method’s precondition states a requirement that can be justified only by looking at its internals, nothing is gained—clients cannot know why the requirement is necessary and will be likely to overlook it. Also, they are likely to stop¹⁸¹ using the method altogether. Meyer therefore postulates the reasonable precondition principle: The contract of a method must be justifiable from the method’s and class’s purpose, without looking at their implementation.

The method next() is supposed to perform two things: (1) It returns the current element and (2) it advances the current position as a side effect. Fortunately, the contract can express this directly in terms of the introduced model fields: The post-condition (4.7) just states that the “next element” is returned, and that the field pos is incremented from its old value.^4.1

Just for illustration, let us translate this back to English (from left to right), by spelling out the meaning of the model fields: The return value is the next element in the output sequence (as it was found before the call), and the iterator is advanced to the next element (or to the end of the sequence, if no more elements remain).

Finding the pre-condition is at first not straightforward. The API documentation states “Returns the next element in the iteration,” without mentioning any condition at all. However, it also states that the method throws a “NoSuchElementException if the iteration has no more elements.” So^1.5.4^4.5^6.3 the pre-condition really is that we have not yet reached the end:

This pre-condition certainly is reasonable in the previously mentioned sense, because it can be understood from the idea that the iterator might have reached the end of the sequence so that no more elements can be extracted.

Another interesting thing about the contracts of the two methods is that they justify precisely the idiomatic loop for using an iterator:

1 ThresholdArrayIterator iter =
2 new ThresholdArrayIterator(data, threshold);
3 while (iter.hasNext()) {
4 Integer cur = iter.next();
5 // work with the element
6 }

The test in line 3 according to (4.6) allows the loop body to execute only if pos ≠ seq.length, but this is precisely the necessary pre-condition (4.8) for calling next() in line 4. Without knowing anything internal about our very special iterator, we can conclude that the code will work!

4.2.3 Contracts, Invariants, and Processing Steps

So far, we have written up contracts of methods by considering their purpose and expected behavior. This is, indeed, the way it should be done, since the clients’ requirements are the best guide toward defining a useful API. Now^1.1 it is time to consider the implementation of the iterator’s methods. From the overall code in Fig. 4.7 it is clear that the logic is not very involved, yet a reusable processing step findNext() has been introduced to arrive at a^1.4.5^1.4.8 truly concise implementation.

This method is especially interesting in the present context, because we have actually found it when pondering how to maintain the invariant (4.5): At the core of the implementation, the index i must always point to a valid output element, or one past the end of the entire sequence. Whenever i accidentally points to an element of a that is too large, i must be^4.1 advanced until “everything is again in order”—but “being in order” simply means that the invariant holds. So, let us look at the method in some more detail.

Non-public methods do not implicitly assume or guarantee the invariant.

Because public methods are the entry and exit points to the class’s code,^4.1 they implicitly assume that the invariant holds at their beginning and must guarantee that it holds in the end. In contrast, private and protected^1.4.5^1.4.8^1.7 methods, as well as package-visible ones, are considered to be part of the implementation and to “look inside” the objects they are working on. Very often, they perform only a small step in a larger operation, so they may break the invariant and leave it to others to fix the invariant later on.

thresholditer.ThresholdArrayIterator

1 private void findNext() {
2 while (i != a.length) {
3 if (a[i] <= threshold)
4 break;
5 else
6 i++;
7 }
8 }

The purpose of findNext(), for example, is to skip elements not part of the result sequence seq, so as to reach the invariant (4.5). But what is the pre-condition of findNext()? Under which circumstance can it fulfill its task? From looking at the code, we must have (4.9): The first part ensures that lines 2 and 3 do not throw throw a NullPointerException, while the other part avoids an ArrayIndexOutOfBoundsException in line 3.

Of course, the latter two conditions derive from the invariant (4.5), as long as that part of the invariant does not get broken before the call—we will look into that presently. However, the first part is problematic, since it is not part of the invariant stated in Section 4.2.1. How can we deduce it?

It is normal to find invariants only with hindsight—document them!

The answer is that we cannot, because that condition is simply missing from the invariant. We deliberately omitted it earlier, because we felt that this textbook should guide you through the normal course of development, not through an artificial setup where the author has divined every detailby clairvoyance. It is usual to find during debugging that you have failed to identify an invariant and that you have consequently broken it at some point. Since this case is so common, you should make it a habit to document precisely those elusive, nonobvious details, because it will save the maintenance programmer from falling into the same trap. So, let us amend the invariant by adding the further condition:

Provide meaningful contracts to internal methods.

Contracts capture the purpose of methods, so it will help the maintenance team immensely if internal methods are also well documented by a pre-condition stating when the method can be legally called and a post-condition^4.1 stating what the method achieves. For findNext(), we have answered the first question already. The second question about its effect is also clear: It (re-)establishes the invariant, so its post-condition is the same as (4.5):

0 ≤ i ≤ a.length && (i = a.length || a[i] ≤ threshold)

But is this really true? Does the method guarantee this post-condition? Let^4.7 us briefly look at the code. The first part about the range of i is maintained by the loop, since the assertion holds initially and i is incremented in the body, where it is less than a.length by the loop’s test. For the second part, we ask: When can the loop ever stop? Well, either when the loop test fails (i.e., i = a.length) or because of the inner break, where we have checked a[i] ≤ threshold just before.

In summary, we have been able to capture the behavior of findNext() very precisely by its contract, and because of this precision we have also been able to argue that the actual code meets the stated contract. We can now fit this contract to the context of the central method next().

We will actually give the explanation of the method next() twice: once in a high-level, trusting sort of way, and once for the disbelieving colleague. We hope to encourage you by the first to wade through the second, and to help you establish the links between the versions. The second version also fulfills our promise from the beginning of this chapter: that contracts enable you to argue very precisely in the presence of fierce opposition.

The contract of next() has been given in Section 4.2.2: It may be called only when pos ≠ seq.length, which internally means i ≠ a.length (and so i is actually inside the array in Fig. 4.8). So line 2 in the following snippet will be OK, and line 3 makes i at most equal toa.length. Although i now potentially points to an element greater than threshold, that gets fixed by findNext() in line 4. As a result, we can safely return in line 5, delivering the promised element as the return value.

thresholditer.ThresholdArrayIterator

1 public Integer next() {
2 Integer tmp = a[i];
3 i++;
4 findNext();
5 return tmp;
6 }

Now for the second version. It is really the same as the previous one, except that it contains explicit references to earlier assertions and formulates all insights, again, as proper assertions. In this way, even the most distrustful team member will have to accept it. Let us first establish that the code runs through without exceptions. In line 2, the array access is OK: a is non-null by invariant (4.10); by invariant (4.5), the index i is in principle within the range of a, but may be one past the end. The latter case is excluded by the method’s pre-condition (4.8). From both together, we can deduce i < a.length at line 2. So after line 3, we have i ≤ a.length and can call findNext() in line 4 according to its pre-condition (4.9). But does next() achieve its purpose—that is, does it establish its post-condition (4.7) and the invariant? First, it obviously returnsseq[\old(pos)], because that element is kept in tmp at line 2 and returned in line 5. Second, it establishes the invariant at the end, because findNext() establishes that in line 4 according to its post-condition. Done!

In summary, contracts for processing steps link the different parts of a class closely and ensure that they work together seamlessly. To exploit this behavior, it is not necessary to go all the way to a semi-formal argument. Rather it is sufficient to trace the assumptions and guarantees up to the level of detail that seems suitable for the desired level of dependability. If you do want to introduce more detail to the argument, read on in Section 4.7.

4.2.4 The Role of Constructors

^4.1The class invariant captures when objects are “OK” or “usable”: Their internal structure is set up so that methods can perform their work properly^1.6 when called from the outside. When an object is newly created, its memory area gets overwritten with 0 bytes, effectively filling the fields with the¹¹¹ default values specified by the Java language. Any further setup beyond this safety precaution has to be done by the constructors (including the field initializers, which conceptually and technically become part of every constructor).

Constructors establish the invariant by initialization.

From the perspective of contracts, public methods can be called right^4.1 after the constructor finishes execution. Since public methods expect the invariant to hold at the beginning, the invariant must be established by the constructors.

Let us check whether the example is correct in this respect. The constructor takes an array and a threshold and then searches for an element no greater than the threshold. The invariant (4.5) about i will hold: Setting i to 0 makes sure it remains inside the array a, and the call tofindNext() according to that method’s post-condition then establishes the second part of (4.5).

thresholditer.ThresholdArrayIterator

1 public ThresholdArrayIterator(int [] a, int threshold) {
2 // avoid side effects
3 this.a = Arrays.copyOf(a, a.length);
4 this.i = 0;
5 this.threshold = threshold;
6 findNext();
7 }

The constructor’s pre-condition enables it to establish the invariant.

The invariant (4.10) stating that a must not be null, which is also part of the pre-condition (4.9) of findNext() in line 6, cannot be guaranteed by the constructor without the caller’s collaboration. The constructor therefore has the following pre-condition:

Constructors can have further post-conditions besides the invariant.

Every constructor must guarantee that the invariant holds after it finishes execution, but it can, of course, guarantee more. Very often, such constructors preset the object’s state with some given value. For example, StringBuilders are set to a passed string and Sockets are connected to some remote port.

In the running example, the developer will expect the iterator to walk through the passed array. The constructor’s post-condition therefore is that the seq comprises precisely the elements less than the threshold and that iteration starts at the first element of that sequence (we use a pseudo-function here, since the earlier notation a_≤[. . . j] refers to the object’s internals):

4.2.5 Pure Methods for Specification

Model fields give a completely external view on an object’s state. They make explicit that the object does have a state, while at the same time hiding its representation. Very often, however, they merely make public some information that is accessible through methods anyway. As an alternative¹⁵⁰^,¹²⁴^,¹⁵¹ to using model fields in specifications, one can also allow calls to¹⁵²^,²³^,⁷⁴^,⁷³ such methods within contracts. To keep the contracts meaningful, one has to require, however, that these methods do not have any side effects on the object’s state—the technical term used to describe this behavior is pure method.

In the iterator example, the method hasNext() is certainly pure: It just looks at the current content of fields a and i to decide whether another result element is available. We could then reformulate the pre-condition (4.8) of next() into

This new pre-condition is clearly equivalent to the old one. It may, however,^4.2.2 be more understandable for developers, because it reflects the idiomatic loop of iterators directly: Before calling next(), you have to call hasNext() to see whether a next element exists.

4.2.6 Frame Conditions: Taming Side Effects

^4.1Assertions capture the program’s state at a particular point in the source code: Whenever that point is reached, the assertion must hold. If we take this view seriously, even for a single object each post-condition would have to describe every one of its model fields, since in principle everymethod call might change every model field—simply by modifying the underlying internal data. Clearly, this would be very unwieldy and cumbersome. Invariants contribute one aspect to a solution, since at least they capture the internals without repeating them at each public method’s contract. This section discusses a complementary mechanism for stating which model fields are not influenced by a method’s side effects.

In the iterator example, nonchanges to model fields would have to be made explicit as follows: The post-condition of hasNext() would have to include pos = \old(pos) and seq = \old(seq), while the post-condition of next() would include only seq = \old(seq), as it already states pos = \old(pos) + 1. Both assertions are really necessary from a logical perspective, because otherwise the caller could not argue that seq and/or pos are the same after the respective calls; the object may, for instance, modify the content of the internal array a.

Of course, from the purpose of the class it is clear that seq does not change during the iteration, so the contracts we have given so far do make^4.3 sense to any developer. They are also useful for arguing about the code’s correctness, which is the main goal of this chapter. From a practical perspective, we would therefore like to keep the contracts as they are, merely adding that “nothing else changes.”

Frame conditions capture your implicit knowledge of side effects.

The problem of stating such “nonchanges” has been investigated widely in the 2000s, because it is both a prerequisite and a fundamental problem when making contracts precise enough for formal verification. The term¹⁵²^,¹³⁴^,²⁰^,¹⁶⁷^,²³⁰ frame condition is used for such statements. In its simplest form, a frame²¹³^,¹⁹⁵^,³⁷^,¹²⁵ condition consists of a modifies clause for a method’s contract. The clause lists those model fields whose content may be influenced by the execution of the method. For instance, the next() method would have the additional specification

modifies pos

The developer must then argue not only that the post-condition is met, but also that the model fields not mentioned in the modifies clause remain unchanged. Unfortunately, making this argument precise involves a substantial logical machinery, which is certainly not suitable for the everyday practical correctness arguments we are aiming at here.

Make side effects explicit in the API.

When you read other developers’ APIs and trust that they are conscientious about documentation, you assume that they will tell you when the object’s state changes. The usual terminology of a “side effect” is revealing at this point: The change may not even be the method’s main purpose; it may be effected only “on the way” toward achieving that purpose. Indeed, those hidden connections are a major motivation for the design guideline of keeping methods that merely read an object’s state separate from those that modify that state.

Assume that model fields not mentioned in the contract remain unchanged.

When all developers obey the rule of making side effects explicit in their contracts, you can, in consequence, assume that any model field not mentioned does not change during a method call. In fact, this is just the usual development practice: API documentation focuses on what a method achieves and leaves implicit those things it does not do. While theorem provers in formal verification may have problems with such an attitude, humans tend to find it obvious and natural.

Pay close attention to assumptions about nonchanges.

The fact that frame conditions cannot be explained easily to theorem provers means that they have a high complexity. To deal with that complexity, professional developers are highly sensitive to situations where changes might occur: They have simply seen too many bugs caused by unexpected side effects that invalidated what they thought they knew about their objects. Whenever they sense possible effects, they will briefly stop to think, and they will try to convince themselves explicitly that a particular aspect of an object has, in fact, not changed.

4.3 Motivating Contracts with Hindsight

We have now discussed design-by-contract by examining two examples and considering varying levels of detail. In subsequent sections, we elaborate a few more points, but the framework is all in place: contracts to specify the behavior of methods, model fields to describe an object’s state from an external perspective, and invariants to capture the consistency conditions on the private parts of an object as well as on its model fields. Now it is time to check what the framework achieves toward helping us write correct programs.

Contracts give you a checklist with the relevant questions.

We said at the beginning of this chapter that the whole purpose of contracts is to get your code working, and that their main contribution is to point you to all the relevant questions, so that you do not accidentally overlook the one crucial detail that breaks your code.

Contracts, then, are like a form that asks you for specific things to achieve a given goal: Have you thought about what the method assumes? Can you state precisely what it achieves and what the caller can expect? Can you describe the objects’ state to clients? Can you sketch what your objects look like internally?

Another point of view is that contracts give you a mental checklist for describing code: Which self-respecting professional pilot would ever dare to take off without having gone through a detailed checklist? Professional software engineers also carry within them such detailed checklists, built from their experience, and design-by-contract is a standard checklist for ensuring the software’s correctness.

Contracts facilitate communication.

If every developer asks the same questions about the code, or fills in the same mental form with the appropriate answers, communication becomes more efficient. If developers even use the same words for these questions, things get really quick. For instance, suppose you get back an unexpected null value from a method. You can then simply simply say to your teammate, “What’s the precise post-condition of that method?” rather than saying, “You know, I have that test case where I call your method and get back null, as I saw in the debugger. Is that your bug or mine?”

Contracts help you write clearer documentation.

APIs are really just plain-language statements of contracts. They, too, must state when a method may be called, what it returns, and what its side effects are. Beginners often forget some of these points, which creates ambiguity and increases the likelihood of bugs. Thinking in terms of contracts reminds you of the points that must be mentioned and explained.

Contracts make you think twice about your code.

The examples have shown that the framework literally makes you think twice about the code: once about the meaning of an object at each point in time when defining the model fields and stating the invariant, and once in the contracts when stating what clients know just before and just after a method executes. The interconnection between those statements then serves to double-check your reasoning.

For instance, we introduced the model field pos into the threshold iterator because we wished to be precise about the post-condition of next(). At the same time, we found that pos could be employed to describe precisely the check performed by hasNext().

Design-by-contract makes you think a third time.

Once the model fields, contracts, and invariants are written up and have been cross-checked, you actually have to think once again, to argue with quite some precision that the methods do obey their contracts. As we have^4.7 seen with the example a ≠ null, invariants very often remain elusive until you go the extra mile of trying to exclude exceptions and to establish postconditions by logical deduction, rather than by just testing and debugging.

The strong interdependencies between model fields, contracts, invariants, and arguments enable you to cross-check the individual reasoning steps in each of the areas. Overall, the confidence in the correctness arguments increases dramatically.

4.4 Invariants and Callbacks

In the context of the OBSERVER pattern, we have pointed out using a^2.1.2 concrete example that the subject must be consistent before it sends out notifications to its observers. The argument there involves a mental execution that eventually leads to an undesirable result. Now, we can be more precise and more general at the same time:

The invariant must hold before invoking other objects’ methods.

This guideline now is really just an immediate consequence of the injunction^4.1 that the class invariant must hold whenever no code of the class is running. Note that even if the other objects happen to be instances of the same class, it is usually not a good idea to call their methods, because they nevertheless may get back to the caller.

Since the problem occurs so often in practice and is easily gotten wrong, let us make the point explicit. In Fig. 4.9, public method 1 in A at some point breaks the invariant, as indicated by the shaded area. It then decides to call method 2 in object B. That method, in turn, decides to call public method 3 inside A. At this point, the program will probably crash: Since method 3 is public, it assumes that the invariant holds, but during the actual execution, this is not the case at all. For instance, if method 1 had left some reference temporarily as null, method 3 will throw aNullPointerException when working with that reference.

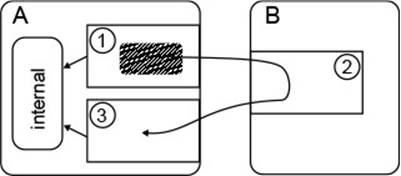
Figure 4.9 Invariants and Calls to the Outside

The proof obligations for class invariants are nonobvious.

^4.1The original proposal to connect invariants with public methods turned²⁴³ out to be insufficient only after some time, which indicates that the earlier¹⁸¹^,¹⁵¹^,¹⁸⁷^,¹⁸⁸^,²¹^,¹²⁴ guideline for calling outside code is not obvious at all. Indeed, researchers have not yet agreed on the best formal rendering of the proof obligations connected with invariants. To gain new perspectives, let us therefore trace a very influential approach.

²¹The approach is to decouple invariants from designated syntactic code points like public methods altogether. Instead, the developer can state explicitly at which points the invariant does hold. “Unpacking” an object means starting to look into its internals, at which point the invariant is known to hold, while it can be broken subsequently. Conversely, “packing” an object requires the developer to argue that the invariant does hold. In this way, when the object is “unpacked” the next time, the invariant holds—because it cannot have been broken in between. The metaphor in the choice of terms is intended (Fig. 4.10(a); see also Fig. 4.1). An object is like a small package: To work with the content, you have to open it, but once you close the package, it remains safe until you reopen the package.

Figure 4.10 Packing and Unpacking Objects

In this approach, the statement “the invariant holds” becomes just a mental “tag” to the object.² Fig. 4.10 illustrates this idea in the form of a state chart: An object is “valid” whenever the invariant holds and “invalid”^4.1 otherwise. This choice of terms reflects the intuition that an object whose in variant does not hold is somehow “broken.” According to the state chart, “unpack” accepts only “valid” objects, so the situation in Fig. 4.9 is ruled out: Method 3 expects a “valid” object A, so method 2 expects a “valid” object A, which method 1 does not provide, since it has just “unpacked” this at the beginning of the gray area.

2. Formally [22], such a “tag” is well understood as a special case of ghost state, which behaves like normal program state during verification but is not available at runtime.

Think of “the invariant holds” as a mental tag to an object.

It is clear that this approach requires very precise bookkeeping of an object’s invariant and is not suitable for informal, everyday reasoning. However, it shows that you are justified in treating “the invariant” as just an abbreviation when reasoning within methods’ code. You can say, for instance, something like this: “Line 3 breaks the invariant, but line 6 reestablishes it after the new text has been inserted.” This is particularly useful in the context of private and protected methods, whose pre- and post-conditions^4.2.3 do not include the invariant implicitly.

Make public methods pay particular attention to the invariants.

The original guideline is nevertheless very useful, because it establishes a warning bell inside the developers’ minds: Before leaving a public method, the object must be put “in order.” Whether the leaving happens by returning^4.1 or by calling outside code is irrelevant. When this rule is obeyed, then the next public method to be called can rely on the invariant.

Our own formulation steers a middle course: Since the class’s code is allowed to break the invariant temporarily, one has to make those parts that do hold explicit in the assertions, or use the abbreviation “and the invariant holds.”

4.5 Checking Assertions at Runtime

Getting programs correct can be a hard task, especially when the data structures and their invariants are complex. It is therefore common practice^1.5.4 to check at crucial points whether the assumptions that the code relies on do actually hold and to throw an exception if they fail. Indeed, maintenance programmers prefer code to fail early with clear error messages rather than with obscure NullPointerExceptions that occur long after the causing code has been executed.

Make assertions executable and use them for debugging.

¹⁸⁰One influential approach, which was pioneered by Meyer’s language Eiffel¹⁵⁰^,⁵⁶ and later taken up by the Java Modeling Language (JML), is to write down the methods’ pre- and post-conditions in a format that can be translated into executable code. During the debugging stage, that code checks the assumptions for the actual execution and signals a logical error when they do not hold. Similarly, Java’s assert statement and Eclipse’s Assert.isTrue evaluate a Boolean expression at runtime and throw an exception when it returns false.

The advantage of such sanity checks is clear: Invalid assumptions are detected early on and pinned down to particular points in the code. In the case of pre- and post-conditions, failures can also be compared directly to the specification and documentation to determine whether the assumption should, in fact, hold according to the code’s goals. The blame can then be clearly attributed to the caller or the method, respectively. Also, developers understand the Boolean expressions immediately, since they remain inside the Java language.

^5.4.8^12.2A huge incentive for runtime assertion checking comes with the practical need to change code when its requirements change. Especially when a different team is involved in these changes, it is easy to miss and break some invariant or other or some implicit pre-condition that the original team had talked about in endless design discussions and that they never bothered to document, because everybody knew it anyway. Leaving the invariant or assumption in the form of an executable assertion, together with a number of test cases, makes it more likely that the maintainers will hit on their mistake early on.

However, these checks are no more than that. In particular, they do not guarantee the absence of logical errors, as the next user interaction or the next test case can easily create a situation where the assertion fails.^4.2^4.7 In contrast, logical deductions about assertions guarantee the absence of errors for all possible executions. Also, executable assertions can obviously cover only computable conditions, while even simple assertions involving “there is some ...” can easily become non-executable. A further disadvantage of runtime checks of assertions is that the checking code itself can be wrong, and must be debugged, maintained, refactored, and otherwise tended.

Methods should not check their pre-conditions.

It is this last disadvantage that motivates a contrasting point of view: Checking code does not contribute to the software’s value and functionality, so it should be abandoned altogether. We have already hinted at this perspective in the discussion of runtime exceptions.^1.5.4

Meyer formulates this insight as the non-redundancy principle: Checking¹⁸¹ a method’s pre-condition is redundant, because logical arguments show that it holds, so the effort of writing the checking code is wasted from the start. Instead, methods should trust their callers to take care of the pre-condition and should get on with their work. Only this approach allows the method’s code to be brief and to the point. Of course, translating a pre-condition stated formally, as is done in Eiffel, does not negate this principle, because no further effort is involved here.

We have, however, pointed out some exceptions to the rule: When a^1.5.4 pre-condition is complex or has been violated several times in the past, then it is very likely that it will be violated again in the future. Checking here is likely to save effort. When you cannot trust the caller to obey the^4.6 pre-condition, you should check. When the consequences of mistakes would be disastrous, you should check. In these situations, the effort of checking must be weighed against the negative consequences of failure, and writing a simple test will usually win out.

4.6 The System Boundary

The non-redundancy principle decrees that methods should never check^4.5 their pre-conditions because that work is wasted: The check will always succeed, or else the broken pre-condition will manifest itself in due course—for instance, through an exception signaling an index out of bounds or an access through a null pointer.

The basis of the non-redundancy principle is trust: The method trusts the caller to obey the pre-condition in each call and proceeds with its computation, taking the pre-condition for granted in making further deductions. Indirectly, this approach assumes an environment in which callers can be trusted, and in particular are neither malicious nor erroneous. Since both assumptions are not always met, the non-redundancy principle must sometimes be dropped to obtain a reliable system.

Methods on the system boundary must be paranoid.

^1.8.7Every practically relevant system must at some point communicate with the outside world (Fig. 4.11). As part of such an interaction, the system will receive data to be processed and will invoke operations, usually by sending commands to other systems. We now examine these two directions separately to rephrase the earlier discussion from Section 4.5 in terms of contracts.

Figure 4.11 Methods on the System Boundary

Never trust incoming data.

The data flowing into the system should always be considered misconstructed and potentially harmful. To illustrate, consider the well-known exploit known as SQL injection. Suppose that the user can enter a new email address, which gets written to the database in the following method:

boundary.FormDataProcessor

public void updateEmail(int userID, String email) {
String sql = "update systemUsers set email='" + email
+ "' where userID='" + userID + "';";
...
}

The new email in the SQL command is surrounded by quotes, as expected. However, a malicious user can simply close that quote to send along arbitrary SQL commands. For instance, here they get themselves root privileges by entering the following “email address,” which starts and ends with a quote. (They have used the same trick before to query the database schema. The following is a string literal from the code.)

boundary.FormDataProcessor.inject

"got@you.com' where userID='1';update systemUsers set
accountType='admin"

The resulting query sent to the database is:

update systemUsers set email='got@you.com'
where userID='1';
update systemUsers set accountType='admin'
where userID='42';

Don’t trust the outside world to obey the system’s pre-conditions.

In terms of contracts, the problem is that the preceding code has the precondition: “The email does not contain unescaped special characters.” As long as the caller obeys this, everything works fine.

A common approach taken to mitigate such threats is shown in Fig. 4.12(a): The system’s functionality is contained in a core component, which never communicates directly with the outside world. That communication is performed by some outer layer, which protects the core like a shell. In the example, the shell would contain the following method, which preprocesses the input to establish the pre-condition of updateEmail by escaping any characters that have a special meaning in SQL.

Figure 4.12 Protecting the System Boundary

boundary.FormDataProcessor

public void acceptFormInput(String email) {
int userID = getSessionUser();
updateEmail(userID, addslashes(email));
}

In the Java environment, the JDT driver accessing the database takes care of quoting and escaping during parameter substitution, as shown below. The protective shell here is found at the level of the database instead of the application. This setup is obviously more robust and also portable between database systems. Furthermore, the application can keep the original string, without escapes, for further processing.

boundary.FormDataProcessor.jdtSolution

String sql = "update systemUsers set email= ? where userID= ?";
PreparedStatement s = c.prepareStatement(sql);
s.setInt(2, userID);
s.setString(1, email);
s.execute();

From the perspective of design-by-contract, the separation between core and shell establishes a dividing line of trust (Fig 4.12(b)): Inside the core, the rules of design-by-contract, and especially the non-redundancy principle, apply and lead to all of their desirable consequences. For this to be possible, all necessary checks and precautions are pushed into the outer shell code. While the shell probably becomes crowded and ugly in the process, the core code with the system’s functionality and business value remains clean and simple.

While malicious attacks certainly do happen, simple mistakes and errors are much more frequent—for example, the user does not enter a positive number as expected, the foreign system sends an ill-formatted XML document, or the data on the hard drive becomes corrupted. The link to design-by-contract remains the same: A method processing these data finds that its pre-condition has been violated.

Fail gracefully.

^4.5Checking the pre-condition here is different from checking it for debugging purposes: You want to give the outer world a meaningful answer, and one^1.5.4 that does not give away internals, such as a stack trace. It is therefore necessary to spend some effort on the question of sensible error messages, as well as on logging the unexpected events.

Be paranoid when invoking potentially harmful operations.

The case of the system invoking operations in the outside can be problematic if damage can be done. Suppose the method B in Fig. 4.12(a) sends out some commands to perform a real-world operation that may harm or damage people or things in that world. One example would be software¹⁵⁷ that controls some medical radiation device. It will contain one part that handles patient data, treatment plans, the user interface, and other administrative elements. Another part will be responsible for actually controlling the hardware to apply preselected radiation dosages, which are derived from the treatment plans.

Check pre-conditions if the consequences of disobedience are severe.

The methods of the hardware driver do have, of course, well-specified preconditions and the developers have probably taken special care in documenting them because they are aware of the potentially disastrous consequences.¹⁵⁷ However, this is not enough: To exclude any possibility of an overdose, the hardware driver should check that its pre-conditions are obeyed. This code is therefore placed in the shell in Fig. 4.12(a).

The checking of pre-conditions may, in fact, not be trivial. For instance, in the railway control domain, the scheduling of trains to tracks is often⁴³ separated from the actual execution of the schedule, which takes place only after checking that the schedule will not lead to collisions.

4.7 Arguing About the Correctness of Programs

A major motivation for applying design-by-contract is that it channels the^4.3 arguments about whether code will work: After specifying the pre- and postcondition of a method, you have to show that, assuming the pre-condition holds initially, the post-condition holds at the end of the execution. Having done that for every method in the program, you know that the code will definitely work.

In most cases, it is sufficient to execute the code mentally to convince^4.1^4.2.3 oneself that it works. However, one can go one step further and argue very precisely, and even mathematically, about code. The seminal insights were laid out by Hoare in the late 1960s and have done much for computer science¹¹⁹ as a practical discipline ever since: Who would like to drive a modern car or fly a modern plane, where many vital systems are controlled by software, without a reliable assurance that these systems will work?

This section closes the remaining gap in the correctness arguments. Many practitioners will say that its content is of only theoretical interest, since all but the most safety-critical software projects lack the time and the resources to actually prove correctness. We have therefore structured the book so that you can skip this section.

We include this material because we hope to create a self-contained presentation that provides the essential insights and formal “tricks” in a form that is accessible to practitioners. Also, we wish to encourage you to think about two points that are highly relevant for any practical software development:

(a) Learn to formulate loop invariants.

(b) Learn to describe the content of your variables at every point.

In regard to point (a), it is almost impossible to write an extended piece of^4.7.2 software without sophisticated loops, and it is very hard to get these loops correct without understanding loop invariants. We have always found, both in teaching and in developing, that understanding loop invariants leads to both shorter and more lucid code and saves much trouble in debugging. Point (b) very often makes the difference between the professional developer and the amateur: The professional knows the meaning of every variable, field, and array in the program and can describe their content at every point in the program in a few succinct words. The amateur, in contrast, has to explain his or her code by describing the eventual execution. The^4.7.1 idea of proof outlines makes this idea precise.

4.7.1 Assignment

At the core of reasoning about contracts, we have to deal with side effects. The question to be answered is, after all, whether the state resulting from setting local variables, object fields, array elements, or something else will fulfill the specified post-condition. Essentially, the task is to capture the behavior of assignment precisely: Once we can handle one assignment, we can handle sequences of them and, as we will see shortly, assignments occurring in if and while statements. We cut the problem to size by considering first^4.7.4.3 local variables and deferring an outlook on heap-allocated data to a later section.

Find a general way of reasoning formally about assignments.

As an introduction to this topic, let us take a problem that lies at the^4.7.2 heart of the later example of summing up the integers in an array. Here, we content ourselves with computing i * j by repeated addition of j. We keep the partial result in s (for “sum”) and we use a counter k. In step number k, we have summed up s = k * j. The step is then shown below: We add one more j and increment k correspondingly. So if s is “correct” before that step, then it should be correct afterward. The assertions express just that.

reason.Assignment.assign1

1 // s = k * j
2 s = s + j;
3 k = k + 1;
4 // s = k * j

But how do we argue that the assertion in line 4 holds? Let us call the initial values of the modified variables S and K, respectively. We can then take a mental execution step: The initial value of s is K * j, so after the assignment in line 2, we have

s = S + j = (K * j) + j

For the next step, mental execution confirms that k has been incremented in line 3:

s = S + j = (K * j) + j ∧ k = K + 1

From this, we have to prove the assertion in line 4. We can do this by unfolding the current values of both variables, which leaves us with proving the simple equality

(K * j) + j = (K + 1) * j

However, the juggling of new names for intermediate values can quickly become unwieldy. Also, we have introduced them on an ad-hoc basis, whenever we felt we needed to refer to “old values.”

Make the reasoning steps mechanical.

Hoare has found an elegant solution to this problem, which is expressed¹¹⁹ in (4.14). There, you see a Hoare triple, which consists of a statement in the center together with a pre-condition to the left and a post-condition to the right. (We mark them as comments; traditionally, they are surrounded by curly braces.) The triple shown here is really a schematic program: The symbols must be replaced by concrete elements from an actual program. Later on, we will see such Hoare rules for the different language constructs. In the literature, the specific rule (4.14) is called theassignment axiom, because it expresses a true statement about an assignment.³

3. If you like mathematics, you might find it interesting that nowadays Hoare rules are not stated as axioms but as derived rules. An axiom is a proposition that is the basis for proving propositions but cannot be proven itself. Introducing an axiom always incurs the danger of inconsistency, referring to the possibility of proving false—in other words, to create a contradiction within the very basis of reasoning. The most famous example is perhaps Frege’s axiomatization of set theory [96], which was later found to contain the well-known Barber paradox. Nowadays, the Hoare rules are proven from the definition of the language’s semantics and the definition of correctness itself (e.g., [192,110,191,217]).

The meanings of x, e, and Q are then clear in (4.14): Expression e is assigned to variable x, and Q is the post-condition. The notation Q[x ← e] means to perform syntactic substitution, in which you take the assertion Q and textually replace all occurrences of x by e (adding, of course, parentheses around e where necessary).

Herein, the expression e must not contain side effects.^4.7.4.1

Compute proof obligations backward.

The point about Hoare rules is that they can be applied mechanically.²¹⁷^,⁶⁶ However, the form of (4.14) forces us to proceed backward, starting from the post-condition and working toward the pre-condition. This may seem slightly bizarre at first, but before judging further, let us try whether it works.

In the example, we wish to have s = k * j in the end, so we apply (4.14) to the assignment in line 3 by setting the following equivalencies (we use a different symbol ≡ for equality between assertions, because ≡ is already used within assertions):

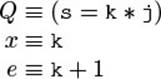
The distinction between the two equality symbols reflects a distinction that is useful in computer science in many places: that between an object level, where the objects of our interest are described, and a meta level, at which we formulate statements about these objects. Another instance of this idea is the use of italics for the schematic variables x, e, and Q in (4.14), which are meta-level tools for talking about the object-level program variables s, i, and k set in typewriter font.

You also know the distinction from the escaping rules of string literals: The double quotes are reserved as meta-level symbols to talk about strings, to specify a string value. Consequently, at the object level of concrete string values, the double quotes are escaped,² as in "\"". Another instance is compiler construction: Grammars are a meta-level tool for specifying the structure of object-level concrete programs.

Computer science simply loves creating languages and tools to talk about other languages, so it is useful to keep the distinction between meta and object levels in mind.²⁵⁵ For instance, XML is used to encode XSLT style sheets, which are used for transforming XML documents. When you write <td><xsl:value-of select="..."/></td>, the td tags are object-level output, and the xsl:value-of is a meta-level XSLT specification talking about a value to be inserted at the point; that value is computed by the meta-level XPath expression in the select attribute.

Let us proceed with the example. We have the replacements for Q, x, and e, so we can compute the pre-condition of line 3 by rule (4.14): Q[x ← e] means replacing k by k + 1 in the concrete Q, which yields

s = (k + 1) * j

Surely, this is more concise than the previous combination of two equalities. Also, we do not have to invent extra names for previous values. Let us proceed with the assignment on line 2:

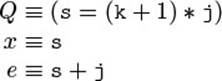
So, as the formal pre-condition of line 2, we get by mechanical substitution

(s + j) = (k + 1) * j

Finally, we can compute (and so could a theorem prover)

(s + j) = (k + 1) * j ≡ s + j = k * j + j ≡ s = k * j

But this is just the given pre-condition! Everything is mechanical computation, except for the very last step, which involves a slight arithmetic deduction that is easily carried out by a theorem prover: If the same thing is added on both sides of an equation, throw the additions away. Since we have reached the pre-condition merely by applying Hoare’s rule, we know that the post-condition does indeed follow from the pre-condition; in other words, the code is correct.

Read Hoare rules backward, starting from the result to be guaranteed.

However, we have promised to justify the single reasoning steps, so it does not do to simply take (4.14) for granted. Formally, it can be deduced from¹⁹²^,¹¹⁰^,¹⁹¹^,²¹⁷ the language semantics and the definition of what “correct” means. Intuitively, one can simply read the rule backward: Sincee does not contain side effects, it is really just a value, and that value gets stored in x. The point to be seen is that Q will pick up that new value from x. If Q must be guaranteed to hold when reading e from x, it must already hold before the assignment, if we put in the value e immediately, without waiting to read it from x later on. This is just what substitution does in (4.14).

Incidentally, the initial reasoning by mental execution can also be captured in a Hoare rule, known as the forward-style assignment axiom. Although you will not usully find it in the literature, it is equally valid and provable from the semantics of¹⁰² the language and the definition of correctness. It performs the choice of new names by existential quantification:

/*P*/x = e /*∃x′.P[x′/x]∧x = e[x′/x]*/

This rule can be read as follows: If P holds before the assignment, then P continues to hold for the old value of x, which we call x′. Furthermore, the new value of x is e, where possible references to x will read the value x′. The disadvantage of cluttering the formulas with new names, of course, remains. We will therefore continue in the more widely used tradition of using the original assignment axiom (4.14).

Put the whole reasoning inline into the code.

Since the rule applications are purely mechanical, they do not have to be explained again and again for every program. Instead, we can simply put the assertions that we described inline into the program. The reader who knows (4.14) can then easily follow us from line 5 to line 3 and from there to the conclusion of line 1, which follows from the given pre-condition.⁴ (We use ⇒ to denote meta-level implications between assertions, and → to denote object-level implications within assertions.)

4. This step is formally justified by a consequence rule [119], but we think it is fairly clear without the formalism.

reason.Assignment.assign2

1 // s = k * j ⇒ s + j = (k + 1) * j
2 s = s + j;
3 // s = (k + 1) * j
4 k = k + 1;
5 // s = k * j

This form of presentation is commonly called a proof outline, because the given assertions guide the correctness proof of the program. The lengthy argument from the previous pages now fits into 5 lines of commented code.

Correctness proofs start with verification condition generation.

Another point to be noted is that the only place where actual reasoning is necessary is the proof of the implication in line 1. The assertion on line 3 is derived mechanically by (4.14), and no intelligence or reasoning is involved here. The same holds for the right-hand side of the implication in line 1. This suggests a two-phase approach to arguing about correctness:

1. Apply Hoare rules mechanically, in a backward fashion, until you hit the stated pre-condition. This process yields a computed pre-condition.⁷⁷^6.1.2 It is also called the weakest pre-condition, because it gives the minimal requirements under which the code will achieve the given post-condition.

2. Prove that the stated pre-condition implies the computed pre-condition.

²²^,¹⁹¹^,²¹⁷^,⁸⁸The first step is called verification condition generation. It reduces the task of proving the correctness of a program to merely showing a set of implications. The latter can then very often be discharged (i.e., proven) automatically by modern theorem provers.

4.7.2 Loops: Summing over an Array

Now that we have mastered the basics, let us get a bit more ambitious. Following you see the code for summing up the elements of an int-array nums. Initially, the array must not be null; in the end, we want sum to hold the sum of all elements. The code is certainly straightforward enough: It just runs an index loop through the array.

reason.ArraySum.sum

Reasoning about loops requires further, nonmechanical insights.

The new element in this example is, of course, the loop. At first, we may be tempted to just apply the assignment axiom (4.14) again and again, twice for each iteration. However, this does not work out, since we cannot know the length of the array nums beforehand.

So let us try to argue practically. Why is the loop “correct”? How does it achieve its purpose? The central insight is certainly that we sum up the array elements “left to right,” as shown in Fig. 4.13. In the figure, the elements up to i (exclusive) have been added to sum, while those with higher indices remain to be processed.

Figure 4.13 Snapshot of Summation

To reason formally, we need to recast this statement in terms of assertions; we have to describe “snapshots of the program state.” We could, for^4.1 instance, capture the image by saying that “sum always contains the sum of all elements up to i (exclusive).”

This can be written a bit more precisely as (4.15). (Since summation in mathematics includes the upper limit, we subtract 1 from i.)

If you think back, we had connected an assertion that “always holds” with^4.1 the idea of an invariant: Except in specific code regions, the invariant holds. Therefore, the statement (4.15) is called the loop invariant.

Loop invariants are practically valuable.

Before we embark on a detailed discussion, let us start with a motivation. Experienced practitioners know the value of loop invariants. For instance, Koenig and Moo in their introductory textbook on C++ programming summarize their value [144, §2.3.2]:

Every useful while statement that we can imagine has an invariant associated with it. Stating the invariant in a comment can make a while much easier to understand.

[ ... ]

Although the invariant is not part of the program text, it is a valuable intellectual tool for designing programs.

The reason for such a strong statement is simple: All loops have to work independently of how many times they iterate, so we have to keep a precise understanding of the content of local variables and object structures through all iterations. The loop invariant is just that: a summary of thatcontent and those structures. Without such a summary overview, there is always a danger that our loops will go astray and will fail to work at some point. Developers who cannot say precisely and succinctly what their variables contain will always be insecure about the working of their code.

Our own experience is that we write simple loops out of habit and complex ones out of a deeper understanding of their invariant. When you have written a few hundred iterations through an array, you do not make explicit the invariant of the next. However, when you encounter a new problem never solved, it is worth formulating an invariant.

A loop invariant holds just before the loop test is executed.

We had associated the class invariant with specific points in the code,^4.1 whether we chose to use the entry and exit points to the class’s code,^4.4 the public methods, or explicit pack/unpack pseudo-statements. At the beginning of these code sections, the invariant was assumed to hold, and we had to argue that it held again when the code sections are left.

A similar reasoning applies to loops: At the beginning of the loop body, the invariant holds. Then, the body modifies the variables and objects involved and thereby breaks the invariant temporarily. However, at the end of the loop body, the invariant must have been reestablished.

Let us look at the example. If (4.15) holds at the beginning of the loop body, and the test ensures that i has not yet reached the end of the array, the invariant holds again after nums[i] has been added to sum and i has been incremented. When we look more closely, we have to ensure that the^4.2.3 array access is valid. We next add a further invariant (4.16): Its first part excludes null-pointer exceptions; its second part, together with the loop test, excludes array-index-out-of-bounds exceptions. (Note that the case i = nums.length is reached in the very last iteration, so i <nums.length would not be an invariant.)

Prove that the invariant holds when the loop starts.

If we wish to know that the invariant holds for the first iteration, we have to prove it. Only the code that sets up the local variables and objects can know something about that state, so it must also be responsible for establishing the invariant. Of course, it will usually have to rely on the method’s precondition and the class invariant in the process. In the example, (4.15) holds by the initialization of sum and i; (4.16) derives the pre-condition and the initialization of i.

The invariant holds when the loop exits by the test returning false.

The real benefit of invariants is that we gain knowledge about the program’s state at the end of the loop. By the preceding construction of the invariant, it always holds at the beginning of the loop body, just before the test: For the first run, we have to argue explicitly; afterward, the invariant is maintained from one execution of the body to the next, independently of how many times that body gets executed. So, the invariant will also hold at the very end, when the test returns false and the loop stops executing. (The treatment of break and continue is somewhat more involved.) In the^4.7.4.2 example, the result deriving from (4.15) and i = nums.length is just the desired post-condition given in the beginning of this section—the loop will actually work!

Loop invariants fit in well with verification condition generation.

Our general plan for correctness arguments is a two-stage process. First, we reduce the program to a set of implications by applying Hoare rules in a backward fashion. Second, we prove the remaining implications. To succeed, we have to give a rule similar to the one for assignment (4.14), but now for loops.

The required rule is actually very simple—it combines the guidelines about loop invariants stated earlier. The formulation (4.17) may look daunting at first, but there is nothing to it. First, the horizontal bar just means “derives” or “implies”: When all the things above have been proven, the thing below has been proven. The thing below in this case is just “the loop is correct with pre-condition P and post-condition Q,” written as a Hoare triple. The things above are just the previous insights: We have to prove that the invariant holds initially, that executing the body maintains the invariant under the assumption that the test yields true, and finally that the desired post-condition derives from the invariant when the loop ends (i.e., when the test returns false). That’s it. (t must not have side-effects.)^4.7.4.1

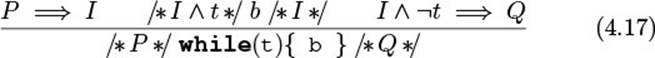
Applying the loop rule is mechanical.

Let us try out the rule on the example, using the notation of a proof outline as shown next, where we note the invariant down in front of the loop. The first proof P ⇒ I at line 4 follows from the initialization of sum and i, since the empty summation from 0 to −1 yields 0. Then, let us check that the loop body maintains the invariant. We do so by noting the invariant at the body’s end, then applying the assignment rule (4.14) backward; the result is noted in line 6, and we have to show that

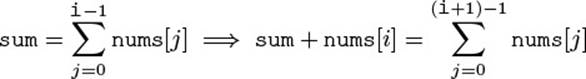
which is clear by a short computation. For the last proof obligation in (4.17), we have to show that the result of the loop in line 12 implies the overall post-condition in line 13. But that, again, is just a simple computation.

reason.ArraySum.sum

The loop invariant captures the partial result achieved so far.

A final question remains: How do you find the loop invariant? As we hope to have clarified, the central point is the practitioner’s insight: The invariant is just a summary of why the loop works. The loop invariant then provides focus. It guides you toward thinking of about loops by asking the question^4.2.3 “What do you know at the start of each iteration?” As with class invariants, it is a good strategy to picture the situation and then to describe the picture in words or formulas.

¹⁰⁷^,¹⁰⁴^–¹⁰⁶In our experience, a more specific question that very often yields new insights is this: What partial result has the loop achieved so far? In the example, Fig. 4.13 suggested that sum may contain the sum of “the left part of the array num,” which was made more precise in (4.15). The beauty of this approach is that in the end, the loop test aborts the loop, at which point the overall result must have been achieved: The invariant’s partial result together with the negated loop test must give the overall desired result.

4.7.3 Conditionals and Loops: Binary Search

The summation example has illustrated the main challenge in verifying code: to find the right loop invariant. At the same time, we have seen that the invariant can often be found by merely describing the partial result accomplished by the loop in the previous iterations. To strengthen this⁷² insight, we apply it to a second example, binary search.

The code that follows is simple enough, when read in the context of its illustration in Fig. 4.14. The code works on a sorted array vals and tries to locate value x. The lower bound l (inclusive) and upper bound u (exclusive) delineate the current search space. Each iteration looks at the value at the middle index m of the search space, decides whether x will be found to the left or to the right of m, and adjusts the search space accordingly.

Figure 4.14 Loop Invariant of Binary Search

reason.BinarySearch.find

1 int l = 0;
2 int u = vals.length;
3 while (l < u) {
4 int m = (l + u) / 2;
5 if (x == vals[m]) {
6 return m;
7 } else if (vals[m] > x) {
8 u = m;
9 } else {
10 l = m + 1;
11 }
12 }
13 return -1;

The result of binary search is either an index at which x has been found in vals or -1 if no such index exists. We can write this formally as the post-condition (4.18) (using also for containment in arrays):

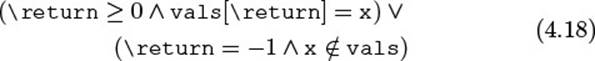
The loop invariant captures the partial result achieved in previous iterations.

So why does this code work? Why does it always find x if it exists in vals? The main insight has already been sketched in Fig. 4.14: By the comparisons performed in the loop and the assumption that vals is sorted, the elements to the left of l are too small and the elements starting at uare too large to contain x—the value x can be found only in the region l to u, if at all. The partial result in this case consists in having eliminated parts of the array as possible locations of x.

To make the reasoning precise, we express this insight more formally. In fact, there are several possible ways of doing so. We might say, for instance, “If x is contained in vals, then it is also found between l and u.” This idea would lead to invariant (4.19) [where we use vals[l..u] for the array slice from l to u (exclusive)]:

This invariant would work out in the end. For instance, going backward through the assignment u=m; in line 8 would yield the proof obligation:

x vals → x vals[l..m]

Since we know in line 8 that vals[m] > x, this proof obligation is clearly solved, since x cannot be found in vals[m..\old(u)]. However, this argument involves some hand waving, because it uses properties of the slice notation that we have not actually proven.

Aim at using elementary formalizations.

So, let us try again. We can, for instance, rephrase (4.19) by making explicit the index at which x occurs. Then we arrive at (4.20), which reads: “If x occurs (at all) at some index i, then that index is found between l and u.” Now we have used only elementary notation, and the substitution for the assignment u=m; replaces u by m only at the end of (4.20). No hand waving is involved, as we shall see later.

A further advantage of such a formulation is that modern theorems provers⁷⁶^,⁷⁵ have highly optimized algorithms for dealing with elementary notation, so there is a good chance they will discharge the proof obligations automatically.

Conditionals yield the test as additional information.

Before we can proceed, we must integrate the if construct to the framework for generating proof obligations—we have to give a Hoare rule for if. Here it is:

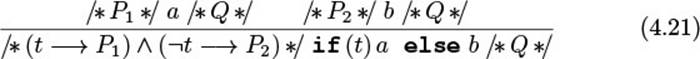
The formal rule (4.21) looks somewhat complex, but it can be understood^4.7.1 easily by reading it backward: To guarantee a post-condition Q, that postcondition must be guaranteed by both branches a and b. We therefore compute the formal pre-conditions P₁ and P₂ for these (at the top), and then assemble the overall pre-condition by adding the information gained by the test. While proving P₁, we can assume additionally that the test returned true; for P₂, we can assume it returned false. As in the case^4.7.4.1^4.7.1 of while, the test cannot have side effects. (We use → as the object-level implication within assertions, and ⇒ as the meta-level implication between assertions.)

Applying the if rule is purely mechanical.

With the above Hoare rules (4.14), (4.17), and (4.21), we are now ready to compute the proof obligations for binary search. The proof outline is shown below. As usual, it must be read backward. We start by injecting the postcondition (4.18) at each return statement. For the return at line 11, the^4.7.4.2 post-condition is immediate from the if rule (4.21). Line 24 is the postcondition for return value -1; line 23 derives from the while rule (4.17), and since u ≤ l contradicts l ≤ i < u, we have

(∀ 0 ≤ i < vals.length. vals[i] = x → false)

which implies

¬(∃ 0 ≤ i < vals.length. vals[i] = x)

which is just a more elaborate way of saying x ∉ vals.

reason.BinarySearch.find

We now examine the invariant according to the while rule (4.17). The invariant holds initially in line 4, simply by the fact that l and u span the entire array. To show that the body maintains the invariant, we proceed backward as usual: We start in line 21, then go backward through the different branches according to the if rule (4.21). The first branch returns, so nothing needs to be done. The second and third branches gain new information by the if tests, as shown in lines 13 and 17.

Line 8 now exhibits very clearly the idea of generating proof obligations: In combining the branches according to (4.21), it keeps only an implication for each branch, but we do not have to think about the original if statement anymore—we can argue just about the formula. The central point to be proven is this: Does line 8 follow from the invariant in line 6? (The exact value of m is irrelevant, so we do not substitute the assignment in line 7 to keep things brief.) A close look at the formula shows that this is the case: The array is sorted and the additional assumption in each case justifies the restriction of the search range. This was the last of the proof obligations—binary search is correct!

Contracts support you all the way to formal reasoning.

We hope that you are convinced that the binary search works with the given invariant. It is, however, interesting to see that we can go even further: If the disbelieving colleague is not satisfied with taking “a close look at the formula,” you can deliver an even more refined and more formal proof by making the implication between line 6 and line 8 precise. So here goes.

Since line 8 is a conjunction, we have to prove the two branches separately; we do only the one first here, as the second is similar. We have to show that

First, let us rename the first quantified variable from i to k to avoid confusion:

Then, we have to show the “for all” quantification on i. Let any i with 0 ≤ i < vals.length be given. We can then replace the repeated implication about by conjunction. The implication to be proven is

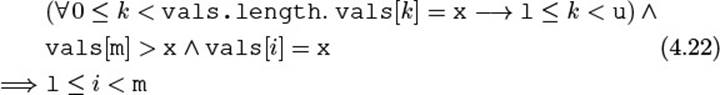
We show this by contradiction. Suppose that ¬(l ≤ i < m), which is the same as i < l V i ≥ m. So there are two cases: If i < l, then the first line of (4.22) yields the contradiction l ≤ i for k = i. If i ≥ m, then we have a contradiction in the second line of (4.22): vals[m] > x and vals is sorted, so that vals[i] > x, contradicting vals[i] = x. In summary, we have proven (4.22), so that the loop body maintains the invariant.

The invariant also captures unchanged facts from before the loop.

In the argument, we have frequently referred to the sortedness of the array. Also, the array accesses in the code work correctly only if l and u never go beyond the array. All in all, we have assumed the additional invariant (4.23), which is, however, maintained by the loop: The variable valsand the array vals do not change at all, and the computation of m in line 7 ensures the inequalities on l and u. (For l ≤ u, observe that m < u by the definition of m and the loop test l < u, so line 18 can never yield l > u.)

4.7.4 Outlook

The material presented in this section has shown that contracts and assertions can serve as a solid foundation for different levels of reasoning, from informal pictorial arguments down to formal mathematical proofs. For brevity, we have omitted some practically relevant constructs. While these have been tackled successfully in recent research projects, full examples¹⁵³^,¹³⁸ are beyond the scope of this book. To avoid leaving you with the unsatisfactory feeling that contracts are, in the end, only a theoretical toy, we conclude this chapter with a brief outlook on the main areas omitted so far. Other language constructs are discussed in Chapter 6.

4.7.4.1 Side Effects in Expressions

The Hoare rules (4.21) and (4.17) for if and while assume that the test t does not contain side effects. The practitioner, of course, immediately thinks of idioms such as the following one for reading from an input stream—do contracts fail even on such everyday code?

while ((n = in.read(buf)) != -1) {
...
}

The answer is simple: Theoreticians consider something like this as “obviously solvable” and usually do not bother to spell out the solution. The²¹⁷^(§4.2) idea is, of course, that any expression with nested side effects can be unrolled into a sequence of simple expressions, similar to what a compiler² does when generating linear machine code. The preceding idiom could, for instance be translated into the following equivalent version, for which proof obligations can be generated by the given rules (using also §4.7.4.2).

while (true) {
int tmp01 = in.read(buf);
n = tmp01;
if (!(tmp01 != -1)) break;
...
}

4.7.4.2 Break, Continue, and Return

A second thing that practitioners do is to preempt the execution of loop bodies by break and continue: At some point, it is clear that some goal has been reached, so there is no use in continuing with the loop or at least with the current iteration.

²¹⁷^{(§2.4.4, §4.5)}The approach to formalizing this behavior is to introduce multiple postconditions, which you can think of as different “channels” for assertions. The central insight is that any statement can do one of three things when it finishes: It can go on to the next statement as usual, it can break the current loop, or it can continue immediately to the end of the loop body. Each of these possible destinations is represented by a different post-condition that must hold at the respective jump target. In a backward application of the following rules, the right thing happens: Normal statements like assignment behave as before, and break and continue inject the correct post-condition.

/* Q[x ← e] */ x = e; /* Q | B | C */
/
* B */ break; /* Q | B | C */
/ * C */ continue; /* Q | B | C */

The post-conditions of the “side channels” B and C are initialized at the surrounding loop, in the proof obligation for the loop body [compare to (4.17)]: A break must establish the loop’s post-condition Q immediately, and a continue must reestablish the loop invariant to admit the next iteration. The break and continue conditions B′ and C′ are irrelevant within the loop, because they relate to a possible outer loop.

Reasoning about return works exactly in the same way: We introduce yet another channel R in the post-condition, and the rule for the return statement selects that channel as its pre-condition. This rule makes precise the notion of “injecting the method’s post-condition” used informally in Section 4.7.3.

4.7.4.3 Aliasing and the Heap

⁴⁶^,¹⁵²A major challenge of formal verification is the precise treatment of the heap and the possibility of aliasing between object references. Over time, many approaches have been developed, and they all come with a substantial⁵⁸^,¹⁹⁵^,²¹³^,³⁸ formal and technical machinery. Here, we can only outline the problem and²⁴⁶^,²⁰^,⁶⁷^,¹⁰²^,¹⁰³ show that the practitioner, unlike the mechanical theorem prover, solves the challenge rather straightforwardly—by drawing pointer diagrams.

Let us start with a simple example of two Point objects, each of which contains integer fields x and y. You will agree that the following test will succeed: a and b are separate objects, and modifying a field in one will leave the other object unchanged.

Point a = new Point();
Point b = new Point();
int bx = b.x;
a.x = 42;
assertEquals(bx, b.x);

Contrast this with a method that does the very same thing. The only difference is that we do not know that a and b are distinct objects. All we could do is to capture this requirement in a pre-condition a ≠ b.

protected void modifyA(Point a, Point b) {
int bx = b.x;
a.x = 42;
assertEquals(bx, b.x);
}

However, the approach of making non-aliasing explicit does not scale: For n distinct objects, we would have to state roughly n² inequalities. Furthermore, frame conditions would have to refer to “all other objects.” At their^4.2.6 core, recent approaches therefore seek to reason explicitly about the heap²¹³^,³⁸^,⁶⁷^,¹⁰²^,¹⁰³^,²⁰ layout and to deduce the necessary inequalities from the layout.

Formally, the challenge is to give a suitable assignment rule for heap-allocated objects: Writes to the heap can hit, in principle, any object on the heap (as C programmers can testify). The simple syntactic substitution in the classical assignment rule (4.14), where the “hit” variable is identified by its name, is no longer sufficient.

A classical and timeless approach is Burstall’s memory model. Burstall⁵⁸^,⁴⁹^,¹⁷⁷^,⁸⁸^,²⁰^,²² observes that different fields, whether in the same class or in different classes, never overlap in any of the instances. For example, the following test works correctly regardless of the concrete objectsa and b involved, because the fields x and y never overlap.

public void burstall(Point a, Point b) {
int by = b.y;
a.x = 42;
assertEquals(by, b.y);
}

Burstall concludes that for verification purposes, one can treat the different fields as named global arrays that are indexed by object pointers. For the source code p.f = e, we generate verification conditions for the array access f[p] = e. As in the classical assignment rule (4.14), the different names of the fields then imply that the fields do not overlap in memory. As a result, a large number of inequalities do not have to be stated explicitly in assertions.

¹⁹⁵^,²¹³Separation logic gives a particularly elegant solution to the challenge. The operator *, called spatial conjunction or simply star, is the logical “and” of two assertions about disjoint parts of the heap. The assignment rule (4.24) can therefore identify the “hit” heap location, again syntactically: If p points to any value e′ before the assignment, then afterward it points to e, and the remainder of the heap, described by Q, is not influenced.³⁸ (In separation logic, Hoare rules are usually applied forward instead of backward.) The fact that Q remains unchanged is derived here from the meaning of [star]: The memory modified by the assignment is found at p, and that area is disjoint from the area to which Q refers.

From a practitioner’s point of view, separation logic is particularly elegant because it usually makes precise the reasoning steps that developers carry out by drawing pointer diagrams on a daily basis. For instance, the running example could be drawn as Fig. 4.15. On a whiteboard, we would cross out the old value x_a and literally overwrite it with the value 42. This also makes it clear that the value x_b is not touched, because it is elsewhere on the whiteboard—it is this intuition of “elsewhere” that the spatial conjunction * captures.

Figure 4.15 A Practical View of Separating Conjunction

Draw pointer diagrams for complex object structures.

The practical lesson to be gleaned from this outlook is that reasoning about the heap can become complex and tricky. It has taken computer science¹¹⁹³⁸^,²¹³^,¹⁹⁵ roughly 35 years, from 1969 to 2005, to progress from the first formalization of program verification itself to a general and scalable formalization of reasoning about the heap. The nice point about this eventual formalization is that it captures essentially the practice of drawing pointer diagrams, which developers have been following in the meantime. Whenever you find yourself thinking about possible aliasing, you are now aware of two things: (1) that it is worth paying attention to details here and (2) that your diagrammatic reasoning rests on a solid foundation.