Programming Scala (2014)

Chapter 10. The Scala Object System, Part I

We’ve learned a lot about Scala’s implementation of object-oriented programming. In this chapter, we’ll discuss more details of the type hierarchy in the standard library, exploring some of those types in depth, such as Predef.

But first, let’s discuss an important feature of the type system called variance under inheritance, which we’ll need to understand before discussing several of the library types described later in this chapter.

We’ll conclude with a discussion of object equality.

Parameterized Types: Variance Under Inheritance

An important difference between Java’s and Scala’s parameterized types (usually called generics in the Java literature) is how variance under inheritance works.

For example, suppose a method takes an argument of type List[AnyRef]. Can you pass a List[String] value? In other words, should a List[String] be considered a subtype of List[AnyRef]? If true, this kind of variance is called covariance, because the supertype-subtype relationship of the container (the parameterized type) “goes in the same direction” as the relationship between the type parameters.

We can also have types that are contravariant, where X[String] is a supertype of X[Any], for some type X.

If a parameterized type is neither covariant nor contravariant, it is called invariant. Conversely, some parameterized types can mix two or more of these behaviors.

Both Java and Scala support covariant, contravariant, and invariant types. However, in Scala, the variance behavior is defined as part of the type declaration using a so-called variance annotation on each type parameter, as appropriate. For covariant type parameters, + is used. For contravariant type parameters, - is used. No annotation is used for invariant type parameters. In other words, the type designer decides how the type should vary under inheritance.

Here are some example declarations (we’ll see examples of real types shortly):

classW[+A] {...} // covariant

classX[-A] {...} // contravariant

classY[A] {...} // invariant

classZ[-A,B,+C] {...} // mixed

In contrast, Java parameterized type definitions do not define the variance behavior under inheritance. Instead, the variance behavior of a parameterized type is specified when the type is used, i.e., at the call site, when variables are declared.

The three kinds of variance notations for Java and Scala and their meanings are summarized in Table 10-1. T^sup is a supertype of T and T_sub is a subtype of T.

Table 10-1. Type variance annotations and their meanings

Back to List—it is actually declared List[+A], which means that List[String] is a subclass of List[AnyRef], so Lists are covariant in the type parameter A. When a type like List has only one covariant type parameter, you’ll often hear the shorthand expression “Lists are covariant” and similarly for contravariant types.

Covariant and invariant types are reasonably easy to understand. What about contravariant types?

Functions Under the Hood

The best example of contravariance is the set of traits FunctionN, such as scala.Function2, where N is between 0 and 22, inclusive, and corresponds to the number of arguments that a function takes. Scala uses these traits to implement anonymous functions.

We’ve been using anonymous functions, also known as function literals, throughout the book. For example:

List(1, 2, 3, 4) map (i => i + 3)

// Result: List(4, 5, 6, 7)

The function expression i => i + 3 is actually syntactic sugar that the compiler converts to the following instantiation of an anonymous subclass of scala.Function1:

val f:Int => Int=newFunction1[Int,Int] {

def apply(i:Int):Int = i + 3

}

List(1, 2, 3, 4) map (f)

// Result: List(4, 5, 6, 7)

NOTE

The conventional name apply for the default method called when an object is followed by an argument list originated with the idea of function application. For example, once f is defined, we call it by applying an argument list to it, e.g., f(1), which is actually f.apply(1).

Historically, the JVM didn’t allow “bare” functions in byte code. Everything had to be in an object wrapper. More recent versions of Java, especially Java 8, relax this restriction, but to enable Scala to work on older JVMs, the compiler has converted anonymous functions into anonymous subclasses of the appropriate FunctionN trait. You’ve probably written anonymous subclasses like this for Java interfaces many times in your Java projects.

The FunctionN traits are abstract, because the method apply is abstract. Note that we defined apply here. The compiler does this for us when we use the more concise literal syntax instead, i => i + 3. That function body is used to define apply.

NOTE

Java 8 adds support for function literals, called lambdas. They use a different implementation than the one used by Scala, because Scala supports older JVMs.

Returning to contravariance, here is the declaration of scala.Function2:

traitFunction2[-T1, -T2, +R] extendsAnyRef

The last type parameter, +R, the is the return type. It is covariant. The leading two type parameters are for the first and second function arguments, respectively. They are contravariant. For the other FunctionN traits, the type parameters corresponding to function arguments are contravariant.

Therefore, functions have mixed variance behavior under inheritance.

What does this really mean? Let’s look at an example to understand the variance ' line-height:normal;vertical-align: baseline'>// src/main/scala/progscala2/objectsystem/variance/func.scX

classCSuper { def msuper() = println("CSuper") } //

classC extendsCSuper { def m() = println("C") }

classCSub extends C { def msub() = println("CSub") }

var f:C => C = (c:C) =>new C //

f = (c:CSuper) =>newCSub //

f = (c:CSuper) =>new C //

f = (c:C) =>newCSub //

f = (c:CSub) =>newCSuper // COMPILATIONERROR!

Define a three-level inheritance hierarchy of classes.

We define one function f as a var so we can keep assigning new functions to it. All valid function instances must be C => C (in other words, Function1[C,C]; note how we can use the literal syntax for the type, too). The values we assign must satisfy the constraints of variance under inheritance for functions. The first assignment is (c: C) => new C (it ignores the argument c).

This function value, (c: CSuper) => new CSub, is valid, because the argument C is contravariant, so CSuper is a valid substitution, while the return value is covariant, so CSub is a valid replacement for C.

Similar to the previous case, but we simply return a C.

Similar to the previous cases, but we simply pass a C.

An error! A function that takes a CSub argument is invalid, because of contravariance, and the return type CSuper is invalid due to covariance.

This script doesn’t produce any output. If you run it, it will fail to compile on the last line, but the other statements will be valid.

Design by Contract explains why these rules make sense. It is a formulation of the Liskov Substitution Principle and we’ll discuss it briefly as a programming tool in Better Design with Design by Contract. For now, let’s try to understand intuitively why these rules work.

The function variable f is of type C => C (that is, Function1[-C,+C]). The first assignment to f matches this type signature exactly.

Now we assign different anonymous function values to f. The whitespace makes the similarities and differences stand out when comparing the original declaration of f and the subsequent reassignments. We keep reassigning to f because we are testing what substitutions are valid for C => C.

The second assignment, (x:CSuper) => CSub, obeys the declaration for contravariant arguments and a covariant return type, but why is this safe?

The key insight is to recall how f will be used and what assumptions we can make about the actual function behind it. When we say its type is C => C, we are defining a <emphasis role="keep-together">contract</emphasis>] that any valid C value can be passed to f and f will never return anything other than a C value.

So, if the actual function has the type (x:CSuper) => CSub, that function not only accepts any C value as an argument, it can also handle any instance of the parent type CSuper or another of its other subtypes, if any. Therefore, because we only pass C instances, we’ll never pass an argument to f that is outside the range of values it promises to accept. In a sense, f is more “permissive” than it needs to be for this use.

Similarly, when it returns only CSub instances, that is also safe, because the caller can handle instances of C, so it can certainly always handle instances of CSub. In this sense, f is more “restrictive” than it needs to be for this use.

The last line in the example breaks both rules for input and output types. Let’s consider what would happen if we allowed that substitution for f.

In this case, the actual f would only know how to handle CSub instances, but the caller would believe that any C instance can be passed to f, so a runtime failure is likely when f is “surprised,” i.e., it tries to call some method that is only defined for CSub, not C. Similarly, if the actual f can return a CSuper, it will “surprise” the caller with an instance that is outside the range of expected return values, the allowed instances of C.

This is why function arguments must be contravariant and return values must be covariant.

Variance annotations only make sense on the type parameters for types, not for parameterized methods, because the annotations affect the behavior of subtyping. Methods aren’t subtyped. For example, the simplified signature for the List.map method looks like this:

sealedabstractclassList[+A] ... { // mixin traits omitted

...

def map[B](f:A => B):List[B] = {...}

...

}

There is no variance annotation on B and if you tried to add one, the compiler would throw an error.

NOTE

The + variance annotation means the parameterized type is covariant in the type parameter. The - variance annotation means the parameterized type is contravariant in the type parameter. No variance annotation means the parameterized type is invariant in the type parameter.

Finally, the compiler checks your use of variance annotations for invalid uses. Here’s what happens if you attempt to define your own function with the wrong annotations:

scala> traitMyFunction2[+T1, +T2, -R]{

| defapply(v1:T1,v2:T2):R=???

| }

<console>:37:error:contravarianttypeRoccursincovariantposition

in type (v1:T1, v2:T2)R of method apply

def apply(v1:T1, v2:T2):R = ???

^

<console>:37:error:covarianttypeT1occursincontravariantposition

in typeT1ofvaluev1

def apply(v1:T1, v2:T2):R = ???

^

<console>:37:error:covarianttypeT2occursincontravariantposition

in typeT2ofvaluev2

def apply(v1:T1, v2:T2):R = ???

^

Note the error messages. The compiler requires function arguments to behave contravariantly and return types to behave covariantly.

Variance of Mutable Types

All the parameterized types we’ve discussed so far have been immutable types. What about the variance behavior of mutable types? The short answer is that only invariance is allowed. Consider this example:

// src/main/scala/progscala2/objectsystem/variance/mutable-type-variance.scX

scala> classContainerPlus[+A](varvalue:A)

<console>:34:error:covarianttypeAoccursincontravariantposition

in typeAofvaluevalue_=

classContainerPlus[+A](var value:A)

^

scala> classContainerMinus[-A](varvalue:A)

<console>:34:error:contravarianttypeAoccursincovariantposition

in type => A of method value

classContainerMinus[-A](var value:A)

^

The problem with a mutable field is that it behaves like a private field with public read and write accessor methods, even if the field is actually public and has no explicit accessor methods.

Recall from Fields in Classes that def value_=(newA: A): Unit+ is the signature the compiler interprets as the setter for variable value. That is, we can write an expression myinstance.value = someA and this method will be called. Note that the first error message uses this method signature and complains that we’re using covariant type A in a contravariant position.

The second error message mentions a method signature => A. That is, a function that takes no arguments and returns an A, just like the by-name parameters we first saw in Call by Name, Call by Value.

Here’s another way to write the declaration using these methods explicitly, which looks more like traditional Java code:

classContainerPlus[+A](var a:A) {

privatevar_value:A = a

def value_=(newA:A):Unit = _value= newA

def value:A = _value

}

Why must the A passed to value_=(newA: A) be contravariant? This doesn’t seem right, because we’re assigning a new value to _value, but if the new value can be a supertype of A, then we’ll get a type error, because _value must be of type A, right?

Actually, that’s the wrong way to think about the situation. The covariant/contravariant rules apply to how subclasses behave relative to superclasses.

Assume for a moment that our declaration is valid. For example, we could instantiate ContainerPlus[C], using our C, CSub, and CSuper from before:

val cp =newContainerPlus(new C) //

cp.value =new C //

cp.value =newCSub //

cp.value =newCSuper //

Type parameter A is now C.

Valid: we’re just using the same type instance.

Valid for the usual object-oriented reasons, since CSub is a subtype of C.

Compilation error, because a CSuper instance can’t be substituted for a C instance.

It’s only when considering subtypes of ContainerPlus that trouble ensues:

val cp: ContainerPlus[C] = new ContainerPlus(new CSub) //

cp.value = new C //

cp.value = new CSub //

cp.value = new CSuper //

Would be valid, if ContainerPlus[+A] were valid.

From the declared type of c, this should be valid and this is why the argument type must be contravariant, but the actual value_= method for the instance can’t accept a C instance, because its value field is of type CSub.

OK.

OK.

The expression labeled illustrates why the method argument needs to be contravariant. The user of c expects the instance to work with C instances. By looking at the actual implementation of value_=, we already know that we can’t actually support contravariance, but let’s ignore that for a moment and consider what happens if we change the variance annotation:

classContainerMinus[-A](var a:A) {

privatevar_value:A = a

def value_=(newA:A):Unit = _value= newA

def value:A = _value

}

We already know from the error messages at the beginning of this section that this is considered OK for the value_= method (even though it isn’t actually OK), but now we get the second error we saw previously. The A is the return type for the value method, so A is in a covariant position.

Why must it be covariant? This is a little more intuitive. Again, the behavior of subtypes is the key. Once again, assume for a moment that the compiler allows us to instantiate ContainerMinus instances:

val cm: ContainerMinus[C] = new ContainerMinus(new CSuper) //

val c: C = cm.value //

val c: CSuper = cm.value //

val c: CSub = cm.value //

Would be valid, if ContainerMinus[-A] were valid.

cm thinks its value method returns a C, but the actual value method for the instance returns a CSuper. Oops…

OK.

Fails for the same reason in line .

So, if you think of a mutable field in terms of a getter and setter method, it appears in both covariant position when read and contravariant position when written. There is no such thing as a type parameter that is both contravariant and covariant, so the only option is for A to be invariant for the type of a mutable field.

Variance in Scala Versus Java

As we said, the variance behavior is defined in the declaration for Scala types, whereas it is defined when used, at the call site, in Java. The client of a type defines the variance behavior, defaulting to invariant. Java doesn’t allow you to specify variance behavior at the definition site, although you can use expressions that look similar. Those expressions define type bounds, which we’ll discuss shortly.

There are two drawbacks of Java’s call-site variance specifications. First, it should be the library designer’s job to understand the correct variance behavior and encode that behavior in the library itself. Instead, it’s the library user who bears this burden. This leads to the second drawback. It’s easy for a Java user to apply an incorrect annotation that results in unsafe code, like in the scenarios we just discussed.

Another problem in Java’s type system is that Arrays are covariant in the type T. Consider this example:

// src/main/java/progscala2/objectsystem/JavaArrays.java

package progscala2.objectsystem;

publicclassJavaArrays {

publicstaticvoid main(String[] args) {

Integer[] array1 = new Integer[] {

new Integer(1), new Integer(2), new Integer(3) };

Number[] array2 = array1; // Compiles fine

array2[2] = new Double(3.14); // Compiles, but throws a runtime error!

}

}

This file compiles without error. However, when you run it with SBT, hilarity ensues:

> run-mainprogscala2.objectsystem.JavaArrays

[info] Running progscala2.objectsystem.JavaArrays

[error] (run-main-4) java.lang.ArrayStoreException:java.lang.Double

java.lang.ArrayStoreException:java.lang.Double

at progscala2.objectsystem.JavaArrays.main(JavaArrays.java:10)

...

What’s wrong? We discussed previously that mutable collections must be invariant in the type parameter to be safe. Because Java arrays are covariant, we’re allowed by the compiler to assign an Array[Integer] instance to an Array[Number] reference. Then the compiler thinks it’s OK to assign any Number to elements of the array, but in fact, the array “knows” internally that it can only accept Integer values (including subtype instances, if any), so it throws a runtime exception, defeating the purpose of static type checking. Note that even though Scala wraps JavaArrays, the Scala class scala.Array is invariant in the type parameter, so it prevents this “hole.”

See Maurice Naftalin and Philip Wadler, Java Generics and Collections, O’Reilly Media, 2006 for more details of Java’s generics and arrays, from which the last example was adapted.

The Scala Type Hierarchy

We already know many of the types in Scala’s type hierarchy. Let’s look at the general structure of the hierarchy and fill in more details. Figure 10-1 shows the large-scale structure. Unless otherwise noted, all the types we’ll discuss here are in the top-level scala package.

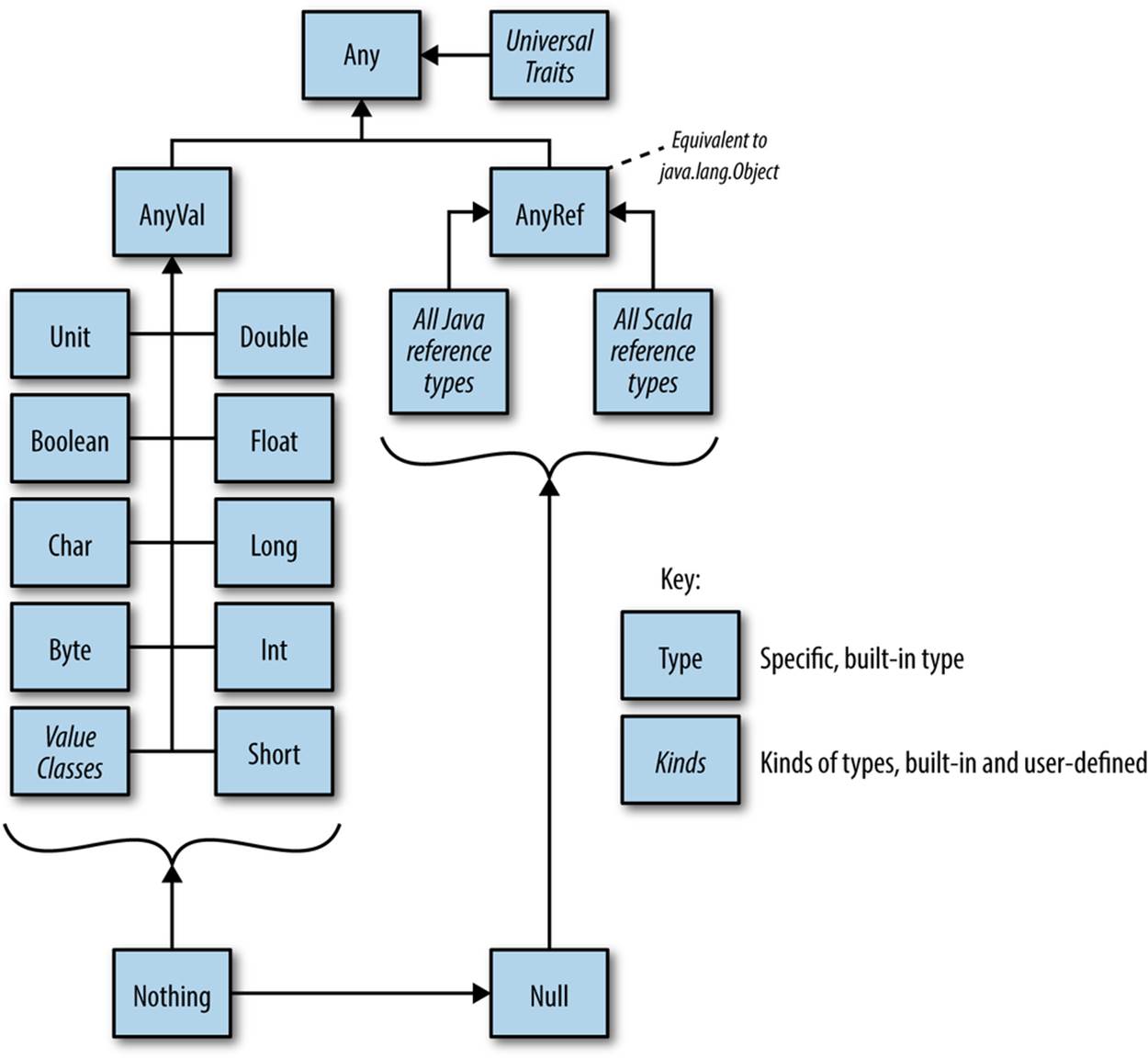
Figure 10-1. Scala’s type hierarchy

At the root of the type hierarchy is Any. It has no parents and three children:

§ AnyVal, the parent of value types and value classes

§ AnyRef, the parent of all reference types

§ Universal Traits, the newly introduced traits for the special uses we discussed in Reference Versus Value Types

AnyVal has nine concrete subtypes, called the value types. Seven are numeric value types: Byte, Char, Short, Int, Long, Float, and Double. The remaining two are nonnumeric value types, Unit and Boolean.

In addition, Scala 2.10 introduced user-defined value classes, which extend AnyVal, as discussed in Reference Versus Value Types.

In contrast, all the other types are reference types. They are derived from AnyRef, which is the analog of java.lang.Object. Java’s object model doesn’t have a parent type of Object that encapsulates both primitives and reference types, because primitive types have special treatment.

NOTE

Before Scala 2.10, the compiler mixed into all instances of Scala reference types a “marker” trait named ScalaObject. The compiler no longer does this and the trait has been removed from Scala 2.11.

We have already learned about many of the reference types and we’ll encounter more as we proceed. However, this is a good time to discuss a few of the widely used types.

Much Ado About Nothing (and Null)

Nothing and Null are two unusual types at the bottom of the type system. Specifically, Nothing is a subtype of all other types, while Null is a subtype of all reference types.

Null is the familiar concept from most programming languages, although they don’t usually define a Null type, just a keyword null that’s “assigned” to a reference to indicate the reference actually has no assigned value. Null is implemented in the compiler as if it has the following declaration:

packagescala

abstractfinalclassNullextendsAnyRef

How can it be both final and abstract? This declaration disallows subtyping and creating your own instances, but the runtime environment provides one instance, the familiar null we know and love (cough, cough, …).

Null is explicitly defined as a subtype of AnyRef, but it is also a subtype of all AnyRef types. This is the type system’s formal way of allowing you to assign null to instances of any reference type. On the other hand, because Null is not a subtype of AnyVal, it is not possible to assignnull to an Int, for example. Hence, Scala’s null behaves exactly like Java’s null behaves, as it must to coexist on the JVM. Otherwise, Scala could eliminate the concept of null and many potential bugs with it.

In contrast, Nothing has no analog in Java, but it fills a hole that exists in Java’s type system. Nothing is implemented in the compiler as if it had the following declaration:

packagescala

abstractfinalclassNothingextendsAny

Nothing effectively extends Any. So, by construction in the type system, Nothing is a subclass of all other types, reference as well as value types. In other words, Nothing subclasses everything, as weird as that sounds.

Unlike Null, Nothing has no instances. Instead, it provides two capabilities in the type system that contribute to robust, type-safe design.

The first capability is best illustrated with our familiar List[\+A] class. We now understand that List is covariant in A, so List[String] is a subtype of List[Any], because String is a subtype of Any. Therefore, a List[String] instance can be assigned to a variable of typeList[Any].

Scala declares a type for the special case of an empty list, Nil. In Java, Nil would have to be a parameterized class like List, but this is unfortunate, because by definition, Nil never holds any elements, so a Nil[String] and a Nil[Any] would be different, but without distinction.

Scala solves this problem by having Nothing. Nil is actually declared like this:

packagescala.collection.immutable

objectNilextendsList[Nothing] withProductwithSerializable

We’ll discuss Product in the next section. Serializable is the familiar Java “marker” interface for objects that can be serialized using Java’s built-in mechanism for this purpose.

Note that Nil is an object and it extends List[Nothing]. There is only one instance of it needed, because it carries no “state” (elements). Because List is covariant in the type parameter, Nil is a subtype of List[A] for all types A. Therefore, we don’t need separate Nil[A] instances. One will do.

Nothing and Null are called bottom types, because they reside at the bottom of the type hierarchy, so they are subtypes of all (or most) other types.

The other use for Nothing is to represent expressions that terminate the program, such as by throwing an exception. Recall the special ??? method in Predef we saw in Nested Types. It can be called in a temporary method definition so the method is concrete, allowing an enclosing, concrete type to compile, but if the method is called, an exception is thrown. Here is the definition of ???:

packagescala

objectPredef {

...

def ??? :Nothing = thrownewNotImplementedError

...

}

Because ??? “returns” Nothing, it can be called by any other function, no matter what type that function returns. Here is a pathological example:

scala> defm(l:List[Int]):List[Int]=lmap(i=>???)

m: (l:List[Int])List[Int]

scala> m(List(1,2,3))

scala.NotImplementedError:animplementationismissing

at scala.Predef$.$qmark$qmark$qmark(Predef.scala:252)

...

Note that m is still expected to return a List[Int] and the definition type checks, even though ??? “returns” Nothing.

More realistically, ??? is called by a method that has been declared, but not yet defined:

/** @return (mean, standard_deviation) */

def mean_stdDev(data:Seq[Double]): (Double, Double) = ???

For normal termination, the scala.sys package defines an exit method, analogous to the exit method in Java’s System. However, sys.exit returns Nothing.

This means that a method can declare that it returns a “normal” type, yet choose to call sys.exit if necessary, and still type check. A common example is the following idiom for processing command-line arguments, but exiting if an unrecognized option is provided:

// src/main/scala/progscala2/objectsystem/CommandArgs.scala

packageprogscala2.objectsystem

objectCommandArgs {

val help = """

|usage: java ... objectsystem.CommandArgs arguments

|where the allowed arguments are:

| -h | --help Show help

| -i | --in | --input path Path for input

| -o | --on | --output path Path for input

|""".stripMargin

def quit(message:String, status:Int):Nothing = { //

if (message.length > 0) println(message)

println(help)

sys.exit(status)

}

caseclassArgs(inputPath:String, outputPath:String) //

def parseArgs(args:Array[String]):Args = {

def pa(args2:List[String], result:Args):Args = args2 match { //

caseNil=> result //

case ("-h" | "--help") :: Nil=> quit("", 0) //

case ("-i" | "--in" | "--input") :: path :: tail => //

pa(tail, result copy (inputPath = path)) //

case ("-o" | "--out" | "--output") :: path :: tail => //

pa(tail, result copy (outputPath = path))

case_=> quit(s"Unrecognized argument ${args2.head}", 1) //

}

val argz = pa(args.toList, Args("", "")) //

if (argz.inputPath == "" || argz.outputPath == "") //

quit("Must specify input and output paths.", 1)

argz

}

def main(args:Array[String]) = {

val argz = parseArgs(args)

println(argz)

}

}

Print an optional message, then the help message, then exit with the specified error status. Following Unix conventions, 0 is used for normal exits and nonzero values are used for abnormal termination. Note that quit returns Nothing.

A case class to hold the settings determined from the argument list.

A nested, recursively invoked function to process the argument list. We use the idiom of passing an Args instance to accumulate new settings (but by making a copy of it).

End of input, so return the accumulated settings.

User asks for help.

For the input argument, accept one of three variants for the option, -i, --in, or --input, followed by a path argument. Note that if the user doesn’t provide a path (and there are no other arguments), the case won’t match.

Call pa on the tail with an updated result.

Repeat for the output argument.

Handle the error of an unrecognized argument.

Call pa to process the arguments.

Verify that the input and output arguments were provided.

I find this example of pattern matching particularly elegant and concise.

This code is compiled when you build the project, so let’s try it in sbt:

> run-mainprogscala2.objectsystem.CommandArgs-f

[info] Running progscala2.objectsystem.CommandArgs -f

Unrecognized argument -f

usage:java...progscala2.objectsystem.CommandArgsarguments

where the allowed arguments are:

-h|--help Showhelp

-i | --in | --input path Pathfor input

-o | --on | --output path Pathfor input

Exception:sbt.TrapExitSecurityExceptionthrownfromthe

UncaughtExceptionHandler in thread "run-main-1"

java.lang.RuntimeException:Nonzeroexitcode: 1

atscala.sys.package$.error(package.scala:27)

[trace] Stacktracesuppressed:runlastcompile:runMainforthefulloutput.

[error] (compile:runMain) Nonzeroexitcode: 1

[error] ...

>run-mainprogscala2.objectsystem.CommandArgs-ifoo-obar

[info] Running progscala2.objectsystem.CommandArgs -i foo -o bar

Args(foo,bar)

[success] ...

We didn’t throw an exception for the invalid argument, but sbt didn’t like the fact that we called exit.

Products, Case Classes, and Tuples

Your case classes mix in the scala.Product trait, which provides a few generic methods for working with the fields of an instance, a Person instance, for example:

scala> caseclassPerson(name:String,age:Int)

defined classPerson

scala> valp:Product=Person("Dean",29)

p:Product = Person(Dean,29) //The case class instance is assignable to a Product variable.

scala> p.productArity

res0:Int = 2 //The number of fields.

scala> p.productElement(0)

res1:Any = Dean //Elements counted from zero.

scala> p.productElement(1)

res1:Any = 29

scala> p.productIteratorforeachprintln

Dean

29

While having generic ways of accessing fields can be useful, its value is limited by the fact that Any is used for the fields’ types, not their actual types.

There are also subtypes of Product for specific arities, up to 22 (for example, scala.Product2 for two-element products). These types add methods for selecting a particular field, with the correct type information preserved. For example, Product2[+T1,+T2] adds these methods:

packagescala

traitProduct2[+T1, +T2] extendsProduct {

abstractdef _1:T1

abstractdef _2:T2

...

}

These methods return the actual type of the field. The type parameters are covariant, because the ProductN traits are only used with immutable types, where reading the field with a method like _1 uses the corresponding type parameter, T1, in covariant position (i.e., only as a return type).

Recall that these methods are the same ones used to access the elements of tuples. In fact, all TupleN types extend the corresponding ProductN trait and provide concrete implementations for these _1 to _N methods, for _N up to and including 22:

scala> valt2=("Dean",29)

t2: (String, Int) = (Dean,29)

scala> t2._1

res0:String = Dean

scala> t2._2

res2:Int = 29

scala> t2._3

<console>:36:error:value_3 isnotamemberof (String, Int)

t2._3

^

There is no third element nor a _3 method for Tuple2.

Why the upper limit of 22? It’s really somewhat arbitrary and you could make the reasonable argument that having 22 elements in a tuple is way too many anyway.

That’s true for human comprehension, but unfortunately, there is a common scenario where exceeding this limit would be useful: in holding the fields (or columns) of large data “records.” It’s not uncommon for SQL and NoSQL data sets to have schemas with more than 22 elements. Tuples are useful, at least for smaller schemas, because they preserve the field (column) order and type. Hence, a 22-element limit is a problem.

It turns out that case classes in Scala 2.10 are also limited to 22 fields, but this implementation restriction has been eliminated in 2.11. Hence, data applications can use a case class for records with more than 22 elements.

NOTE

In Scala 2.10 and earlier, case classes are limited to 22 fields or less. This limitation is removed in Scala 2.11.

Hopefully, the 22-element limit for traits and products will be removed in a future release of Scala.

The Predef Object

For your convenience, whenever you compile code, the Scala compiler automatically imports the definitions in the top-level Scala package, called scala, as well as the definitions in the java.lang package (just like javac). Hence, many common Java and Scala types can be used without explicitly importing them or using fully qualified names. In addition, the compiler imports the definitions in the Predef object that provides a number of useful definitions, many of which we’ve discussed previously.

Let’s round out the features provided by Predef. Note that a number of changes are being introduced in the Scala 2.11 version of Predef, most of which are not visible. We’ll discuss the 2.11 version.

Implicit Conversions

First, Predef defines many implicit conversions. One group of conversions includes wrappers around the AnyVal types:

@inline implicitdef byteWrapper(x:Byte) =new runtime.RichByte(x)

@inline implicitdef shortWrapper(x:Short) =new runtime.RichShort(x)

@inline implicitdef intWrapper(x:Int) =new runtime.RichInt(x)

@inline implicitdef charWrapper(c:Char) =new runtime.RichChar(c)

@inline implicitdef longWrapper(x:Long) =new runtime.RichLong(x)

@inline implicitdef floatWrapper(x:Float) =new runtime.RichFloat(x)

@inline implicitdef doubleWrapper(x:Double) =new runtime.RichDouble(x)

@inline implicitdef booleanWrapper(x:Boolean) =new runtime.RichBoolean(x)

The Rich* types add additional methods, like comparison methods such as <= and compare. The @inline annotation encourages the compiler to “inline” the method call, i.e., eliminate it by inserting the new runtime.RichY(x) logic directly.

Why have two separate types for bytes, for example? Why not put all the methods in Byte itself? The reason is that the extra methods would force an instance to be allocated on the heap, due to implementation requirements for byte code. Byte instances, like the other AnyVal types, are not actually heap-allocated, but represented as Java’s byte primitives. So, having separate Rich* types avoids the heap allocation except for those times when the extra methods are needed.

There are also methods for wrapping Java’s mutable arrays in instances of scala.collection.mutable.WrappedArray, which adds many of the collection methods we discussed in Chapter 6:

implicitdef wrapIntArray(xs:Array[Int]):WrappedArray[Int]

implicitdef wrapDoubleArray(xs:Array[Double]):WrappedArray[Double]

implicitdef wrapLongArray(xs:Array[Long]):WrappedArray[Long]

implicitdef wrapFloatArray(xs:Array[Float]):WrappedArray[Float]

implicitdef wrapCharArray(xs:Array[Char]):WrappedArray[Char]

implicitdef wrapByteArray(xs:Array[Byte]):WrappedArray[Byte]

implicitdef wrapShortArray(xs:Array[Short]):WrappedArray[Short]

implicitdef wrapBooleanArray(xs:Array[Boolean]):WrappedArray[Boolean]

implicitdef wrapUnitArray(xs:Array[Unit]):WrappedArray[Unit]

Why are there separate methods for each AnyVal type? Each one uses a custom subclass of WrappedArray that exploits the fact that Java arrays of primitives are more efficient than arrays of boxed elements, so the less efficient, generic implementation for reference types is avoided.

There are similar methods for converting to scala.collection.mutable.ArrayOps. The only difference between WrappedArray and ArrayOps is that transformation functions for WrappedArray, such as filter, will return a new WrappedArray, while the corresponding functions in ArrayOps return Arrays.

Like WrappedArray and ArrayOps, there are analogous types for Strings, scala/collection/immutable/WrappedString and scala/collection/immutable/StringOps, which add collection methods to Strings, treating them like collections of Chars. Hence, Predefdefines conversions between String and these types:

implicitdef wrapString(s:String):WrappedString

implicitdef unwrapString(ws:WrappedString):String

implicitdef augmentString(x:String):StringOps

implicitdef unaugmentString(x:StringOps):String

NOTE

Having pairs of similar wrapper types, like WrappedArray/ArrayOps and WrappedString/StringOps, is a bit confusing, but fortunately the implicit conversions are invoked automatically, selecting the correct wrapper type for the method you need.

There are other methods for converting between Java’s boxed types for primitives and Scala’s AnyVal types. They make Java interoperability easier:

implicitdef byte2Byte(x:Byte) = java.lang.Byte.valueOf(x)

implicitdef short2Short(x:Short) = java.lang.Short.valueOf(x)

implicitdef char2Character(x:Char) = java.lang.Character.valueOf(x)

implicitdef int2Integer(x:Int) = java.lang.Integer.valueOf(x)

implicitdef long2Long(x:Long) = java.lang.Long.valueOf(x)

implicitdef float2Float(x:Float) = java.lang.Float.valueOf(x)

implicitdef double2Double(x:Double) = java.lang.Double.valueOf(x)

implicitdef boolean2Boolean(x:Boolean) = java.lang.Boolean.valueOf(x)

implicitdefByte2byte(x:java.lang.Byte):Byte = x.byteValue

implicitdefShort2short(x:java.lang.Short):Short = x.shortValue

implicitdefCharacter2char(x:java.lang.Character):Char = x.charValue

implicitdefInteger2int(x:java.lang.Integer):Int = x.intValue

implicitdefLong2long(x:java.lang.Long):Long = x.longValue

implicitdefFloat2float(x:java.lang.Float):Float = x.floatValue

implicitdefDouble2double(x:java.lang.Double):Double = x.doubleValue

implicitdefBoolean2boolean(x:java.lang.Boolean):Boolean = x.booleanValue

Finally, in Scala 2.10, there is a group of implicit conversions that prevent null from being accepted as a value for an assignment. We’ll just show one example, for Byte:

implicitdefByte2byteNullConflict(x:Null):Byte = sys.error("value error")

It triggers the following error:

scala> valb:Byte=null

<console>:23:error:typemismatch;

found :Null(null)

required:Byte

Note that implicit conversions are not applicable because they are ambiguous:

bothmethodByte2byteNullConflictinclassLowPriorityImplicitsof

type (x:Null)ByteandmethodByte2byteinobjectPredefoftype (x:Byte)Byte

are possible conversion functions from Null(null) to Byte

val b:Byte = null

^

That works OK, but the error message isn’t really that clear. It’s complaining about ambiguous implicits, which the library deliberately introduced, but really it should just tell us more directly that we shouldn’t assign null to anything.

Here’s the error message produced by Scala 2.11:

scala> valb:Byte=null

<console>:7:error:anexpressionoftypeNullisineligiblefor

implicit conversion

val b:Byte = null

^

Scala 2.11 eliminates the conversion methods and provides a better, more concise error message.

Type Definitions

Predef defines several types and type aliases.

To encourage the use of immutable collections, Predef defines aliases for the most popular, immutable collection types:

typeMap[A, +B] = collection.immutable.Map[A, B]

typeSet[A] = collection.immutable.Set[A]

typeFunction[-A, +B] =Function1[A, B]

Two convenient aliases for two- and three-element tuples have been deprecated in 2.11, on the grounds that they aren’t used enough and don’t add enough value to justify their existence:

typePair[+A, +B] =Tuple2[A, B]

typeTriple[+A, +B, +C] =Tuple3[A, B, C]

Other Predef type members support type inference:

final class ArrowAssoc[A] extends AnyVal

Used to implement the a -> b literal syntax for creating two-element tuples. We discussed it in Implicit Conversions.

sealed abstract class <:<[-From, +To] extends (From) => To with Serializable

Witnesses that type From is a subtype of type To. We discussed it in Implicit Evidence.

sealed abstract class =:=[-From, +To] extends (From) => To with Serializable

Witnesses that types From and To are equal. We also mentioned it in Implicit Evidence.

type Manifest[T] = reflect.Manifest[T]

Used to retain type information that’s lost in the JVM’s type erasure. There is a similar type OptManifest. We’ll discuss them in Class Tags, Type Tags, and Manifests.

Other types, like scala.collection.immutable.List, are made visible through nested imports within Predef. Also, companion objects for some of the types are also made visible, such as =:=, Map, and Set.

Condition Checking Methods

Sometimes you want to assert a condition is true, perhaps to “fail fast” and especially during testing. Predef defines a number of methods that assist in this goal:

def assert(assertion: Boolean)

Test that assertion is true. If not, throw a java.lang.AssertionError.

def assert(assertion: Boolean, message: => Any)

Similar, but with an additional argument that’s converted to a string message.

def assume(assertion: Boolean)

Identical to assert, but conveys the meaning that the condition is assumed to be true when entering a block of code, such as a method.

def assume(assertion: Boolean, message: => Any)

Similar, but with an additional argument that’s converted to a string message.

def require(requirement: Boolean)

Identical to assume, but the Scaladoc says it conveys the meaning that the caller failed to satisfy some requirement; it could also convey the meaning that an implementation could not achieve a required result.

def require(requirement: Boolean, message: => Any)

Similar, but with an additional argument that’s converted to a string message.

It’s not shown, but all of these assertion methods are annotated with @elidable(ASSERTION). The @elidable annotation tells the compiler not to generate byte code for a definition unless the argument to the annotation (ASSERTION in this case) is above a threshold that is specified during compilation. For example, scalac -Xelide-below 2000 suppresses code generation for all annotated definitions with argument values below 2000. 2000 happens to be the value defined for ASSERTION in the elidable companion object. See the Scaladoc page for more information on @elidable.

Input and Output Methods

We’ve enjoyed the convenience of writing println("foo") instead of the more verbose Java equivalent, System.out.println("foo")). Predef gives us four variants for writing strings to stdout:

def print(x: Any): Unit

Convert x to a String and write it to stdout, without adding a line feed at the end automatically.

def printf(format: String, xs: Any*): Unit

Format a printf-style string using format as the format and the rest of the arguments xs, then write the resulting String to stdout, without adding a line feed at the end automatically.

def println(x: Any): Unit

Like print, but appends a line feed at the end automatically.

def println(): Unit

Writes a blank line to stdout.

Predef in Scala 2.10 also defines several functions for reading input from stdin. However, these functions are deprecated in Scala 2.11. Instead, they are defined in a new scala.io.ReadStdin object that should be used instead. Otherwise, the method signatures and behaviors are the same:

def readBoolean(): Boolean

Reads a Boolean value from an entire line from stdin.

def readByte(): Byte

Reads a Byte value from an entire line from stdin.

def readChar(): Char

Reads a Char value from an entire line from stdin.

def readDouble(): Double

Reads a Double value from an entire line from stdin.

def readFloat(): Float

Reads a Float value from an entire line from stdin.

def readInt(): Int

Reads an Int value from an entire line from stdin.

def readLine(text: String, args: Any*): String

Prints formatted text to stdout and reads a full line from stdin.

def readLine(): String

Reads a full line from stdin.

def readLong(): Long

Reads a Long value from an entire line from stdin.

def readShort(): Short

Reads a Short value from an entire line from stdin.

def readf(format: String): List[Any]

Reads in structured input from stdin as specified by the format specifier.

def readf1(format: String): Any

Reads in structured input from stdin as specified by the format specifier, returning only the first value extracted, according to the format specification.

def readf2(format: String): (Any, Any)

Reads in structured input from stdin as specified by the format specifier, returning only the first two values extracted, according to the format specification.

def readf3(format: String): (Any, Any, Any)

Reads in structured input from stdin as specified by the format specifier, returning only the first three values extracted, according to the format specification.

NOTE

You can override the java.io.Reader used for stdin or the java.io.OutputStreams used for stdout or stderr using methods in scala.Console.

Miscellaneous Methods

Finally, there are a few more useful methods in Predef to highlight:

def ???: Nothing

Called in a method body for a method that is actually unimplemented. It provides a concrete definition for the method, allowing enclosing types to compile as concrete (as opposed to abstract). However, if called, the method throws a scala.NotImplementedError. We first discussed it in Nested Types.

def identity[A](x: A): A

Simply returns the argument x. It is useful for passing to combinator methods when no change is required. For example, a work flow calls map to transform the elements of a collection, passing it a configurable function to do the transformation. Sometimes, no transformation is required, so you’ll pass identity instead.

def implicitly[T](implicit e: T): T

Used when an implicit argument list is specified with the type shorthand [T : M], in which case the compiler adds an implicit argument list of the form (implicit arg: M[T]). (The actual name isn’t arg, but something unique synthesized by the compiler.) Calling implicitlyreturns the argument arg. Discussed previously in Using implicitly.

Now let’s consider a very important topic in object-oriented design, checking the equality of objects.

Equality of Objects

Implementing a reliable equality test for instances is difficult to do correctly. Joshua Block’s popular book, Effective Java (Addison-Wesley), and the Scaladoc page for AnyRef.eq describe the requirements for a good equality test.

Martin Odersky, Lex Spoon, and Bill Venners wrote a very good article on writing equals and hashCode methods, How to Write an Equality Method in Java. Recall that these methods are created automatically for case classes.

In fact, I never write my own equals and hashCode methods. I find that any object that I use where I might need to test for equality or to use it as a Map key (where hashCode is used) should be a case class!

CAUTION

Some of the equality methods have the same names as equality methods in other languages, but the semantics are sometimes different!

Let’s look at the different methods used to test equality.

The equals Method

We’ll use a case class to demonstrate how the different equality methods work:

// src/main/scala/progscala2/objectsystem/person-equality.sc

caseclassPerson(firstName:String, lastName:String, age:Int)

val p1a =Person("Dean", "Wampler", 29)

val p1b =Person("Dean", "Wampler", 29)

val p2 =Person("Buck", "Trends", 30)

The equals method tests for value equality. That is, obj1 equals obj2 is true if both obj1 and obj2 have the same value. They do not need to refer to the same instance:

p1a equals p1a // = true

p1a equals p1b // = true

p1a equals p2 // = false

p1a equals null // = false

null equals p1a // throws java.lang.NullPointerException

null equals null // throws java.lang.NullPointerException

Hence, equals behaves like the equals method in Java and the eql? method in Ruby, for example.

The == and != Methods

Whereas == is an operator in many languages, it is a method in Scala. In Scala 2.10, == is defined as final in Any and it delegates to equals. A different implementation is used in 2.11, but the behavior is effectively the same:

p1a == p1a // = true

p1a == p1b // = true

p1a == p2 // = false

Hence, it behaves exactly like equals, namely it tests for value equality. The exception is the behavior when null is on the lefthand side:

p1a == null // = false

null == p1a // = false

null == null // = true (compiler warns that it's always true)

Should null == null be true? Actually, a warning is emitted:

<console>:8: warning: comparing values of types Null and Null using `=='

will always yield true

As you would expect, != is the negation, i.e., it is equivalent to !(obj1 == obj2):

p1a != p1a // = false

p1a != p1b // = false

p1a != p2 // = true

p1a != null // = true

null != p1a // = true

null != null // = false (compiler warns that it's always false.)

NOTE

In Java, C++, and C#, the == operator tests for reference, not value equality. In contrast, Scala’s == operator tests for value equality.

The eq and ne Methods

The eq method tests for reference equality. That is, obj1 eq obj2 is true if both obj1 and obj2 point to the same location in memory. These methods are only defined for AnyRef:

p1a eq p1a // = true

p1a eq p1b // = false

p1a eq p2 // = false

p1a eq null // = false

null eq p1a // = false

null eq null // = true (compiler warns that it's always true.)

Just as the compiler issues a warning for null == null, it issues the same warning for null eq null.

Hence, eq behaves like the == operator in Java, C++, and C#.

The ne method is the negation of eq, i.e., it is equivalent to !(obj1 eq obj2):

p1a ne p1a // = false

p1a ne p1b // = true

p1a ne p2 // = true

p1a ne null // = true

null ne p1a // = true

null ne null // = false (compiler warns that it's always false.)

Array Equality and the sameElements Method

Comparing the contents of two Arrays doesn’t have an obvious result in Scala:

Array(1, 2) == Array(1, 2) // = false

That’s a surprise! Thankfully, there’s a simple solution in the form of the sameElements method:

Array(1, 2) sameElements Array(1, 2) // = true

Actually, it’s better to remember that Arrays are the mutable, raw Java arrays we know and love, which don’t have the same methods we’re accustomed to in the Scala collections library.

So, if you’re tempted to compare arrays, consider whether or not it would be better to work with sequences instead (an argument for not using alternatives is when you really need the performance benefits of arrays).

In contrast, for example, Lists work as you would expect:

List(1, 2) == List(1, 2) // = true

List(1, 2) sameElements List(1, 2) // = true

Recap and What’s Next

We discussed important topics in Scala’s object system, such as the behavior under inheritance, the features in Predef, the fundamentals of the type hierarchy, and equality.

Next we’ll complete our discussion of the object system by examining the behavior of member overriding and resolution rules.