Functional Programming in Scala (2015)
Part 2. Functional design and combinator libraries
Chapter 9. Parser combinators
In this chapter, we’ll work through the design of a combinator library for creating parsers. We’ll use JSON parsing (http://mng.bz/DpNA) as a motivating use case. Like chapters 7 and 8, this chapter is not so much about parsing as it is about providing further insight into the process of functional design.
What is a parser?
A parser is a specialized program that takes unstructured data (such as text, or any kind of stream of symbols, numbers, or tokens) as input, and outputs a structured representation of that data. For example, we can write a parser to turn a comma-separated file into a list of lists, where the elements of the outer list represent the records, and the elements of each inner list represent the comma-separated fields of each record. Another example is a parser that takes an XML or JSON document and turns it into a tree-like data structure.
In a parser combinator library, like the one we’ll build in this chapter, a parser doesn’t have to be anything quite that complicated, and it doesn’t have to parse entire documents. It can do something as elementary as recognizing a single character in the input. We then use combinators to assemble composite parsers from elementary ones, and still more complex parsers from those.
This chapter will introduce a design approach that we’ll call algebraic design. This is just a natural evolution of what we’ve already been doing to different degrees in past chapters—designing our interface first, along with associated laws, and letting this guide our choice of data type representations.
At a few key points during this chapter, we’ll give more open-ended exercises, intended to mimic the scenarios you might encounter when writing your own libraries from scratch. You’ll get the most out of this chapter if you use these opportunities to put the book down and spend some time investigating possible approaches. When you design your own libraries, you won’t be handed a nicely chosen sequence of type signatures to fill in with implementations. You’ll have to make the decisions about what types and combinators you need, and a goal in part 2 of this book has been to prepare you for doing this on your own. As always, if you get stuck on one of the exercises or want some more ideas, you can keep reading or consult the answers. It may also be a good idea to do these exercises with another person, or compare notes with other readers online.
Parser combinators versus parser generators
You might be familiar with parser generator libraries like Yacc (http://mng.bz/w3zZ) or similar libraries in other languages (for instance, ANTLR in Java: http://mng.bz/aj8K). These libraries generate code for a parser based on a specification of the grammar. This approach works fine and can be quite efficient, but comes with all the usual problems of code generation—the libraries produce as their output a monolithic chunk of code that’s difficult to debug. It’s also difficult to reuse fragments of logic, since we can’t introduce new combinators or helper functions to abstract over common patterns in our parsers.
In a parser combinator library, parsers are just ordinary first-class values. Reusing parsing logic is trivial, and we don’t need any sort of external tool separate from our programming language.
9.1. Designing an algebra, first
Recall that we defined algebra to mean a collection of functions operating over some data type(s), along with a set of laws specifying relationships between these functions. In past chapters, we moved rather fluidly between inventing functions in our algebra, refining the set of functions, and tweaking our data type representations. Laws were somewhat of an afterthought—we worked out the laws only after we had a representation and an API fleshed out. There’s nothing wrong with this style of design,[1] but here we’ll take a different approach. We’ll start with the algebra (including its laws) and decide on a representation later. This approach—let’s call it algebraic design—can be used for any design problem but works particularly well for parsing, because it’s easy to imagine what combinators are required for parsing different kinds of inputs.[2] This lets us keep an eye on the concrete goal even as we defer deciding on a representation.
1 For more about different functional design approaches, see the chapter notes for this chapter.
2 As we’ll see, there’s a connection between algebras for parsers and the classes of languages (regular, context-free, context-sensitive) studied by computer science.
There are many different kinds of parsing libraries.[3] Ours will be designed for expressiveness (we’d like to be able to parse arbitrary grammars), speed, and good error reporting. This last point is important. Whenever we run a parser on input that it doesn’t expect—which can happen if the input is malformed—it should generate a parse error. If there are parse errors, we want to be able to point out exactly where the error is in the input and accurately indicate its cause. Error reporting is often an afterthought in parsing libraries, but we’ll make sure we give careful attention to it.
3 There’s even a parser combinator library in Scala’s standard libraries. As in the previous chapter, we’re deriving our own library from first principles partially for pedagogical purposes, and to further encourage the idea that no library is authoritative. The standard library’s parser combinators don’t really satisfy our goals of providing speed and good error reporting (see the chapter notes for some additional discussion).
OK, let’s begin. For simplicity and for speed, our library will create parsers that operate on strings as input.[4] We need to pick some parsing tasks to help us discover a good algebra for our parsers. What should we look at first? Something practical like parsing an email address, JSON, or HTML? No! These tasks can come later. A good and simple domain to start with is parsing various combinations of repeated letters and gibberish words like "abracadabra" and "abba". As silly as this sounds, we’ve seen before how simple examples like this help us ignore extraneous details and focus on the essence of the problem.
4 This is certainly a simplifying design choice. We can make the parsing library more generic, at some cost. See the chapter notes for more discussion.
So let’s start with the simplest of parsers, one that recognizes the single character input 'a'. As in past chapters, we can just invent a combinator for the task, char:
def char(c: Char): Parser[Char]
What have we done here? We’ve conjured up a type, Parser, which is parameterized on a single parameter indicating the result type of the Parser. That is, running a parser shouldn’t simply yield a yes/no response—if it succeeds, we want to get a result that has some useful type, and if it fails, we expect information about the failure. The char('a') parser will succeed only if the input is exactly the character 'a' and it will return that same character 'a' as its result.
This talk of “running a parser” makes it clear our algebra needs to be extended somehow to support that. Let’s invent another function for it:
def run[A](p: Parser[A])(input: String): Either[ParseError,A]
Wait a minute; what is ParseError? It’s another type we just conjured into existence! At this point, we don’t care about the representation of ParseError, or Parser for that matter. We’re in the process of specifying an interface that happens to make use of two types whose representation or implementation details we choose to remain ignorant of for now. Let’s make this explicit with a trait:

What’s with the funny Parser[+_] type argument? It’s not too important for right now, but that’s Scala’s syntax for a type parameter that is itself a type constructor.[5] Making ParseError a type argument lets the Parsers interface work for any representation of ParseError, and making Parser[+_] a type parameter means that the interface works for any representation of Parser. The underscore just means that whatever Parser is, it expects one type argument to represent the type of the result, as in Parser[Char]. This code will compile as it is. We don’t need to pick a representation for ParseError or Parser, and we can continue placing additional combinators in the body of this trait.
5 We’ll say much more about this in the next few chapters.
Our char function should satisfy an obvious law—for any Char, c,
run(char(c))(c.toString) == Right(c)
Let’s continue. We can recognize the single character 'a', but what if we want to recognize the string "abracadabra"? We don’t have a way of recognizing entire strings right now, so let’s add that:
def string(s: String): Parser[String]
Likewise, this should satisfy an obvious law—for any String, s,
run(string(s))(s) == Right(s)
What if we want to recognize either the string "abra"or the string "cadabra"? We could add a very specialized combinator for it:
def orString(s1: String, s2: String): Parser[String]
But choosing between two parsers seems like something that would be more generally useful, regardless of their result type, so let’s go ahead and make this polymorphic:
def or[A](s1: Parser[A], s2: Parser[A]): Parser[A]
We expect that or(string("abra"),string("cadabra")) will succeed whenever either string parser succeeds:
run(or(string("abra"),string("cadabra")))("abra") == Right("abra")
run(or(string("abra"),string("cadabra")))("cadabra") == Right("cadabra")
Incidentally, we can give this or combinator nice infix syntax like s1 | s2 or alternately s1 or s2, using implicits like we did in chapter 7.
Listing 9.1. Adding infix syntax to parsers
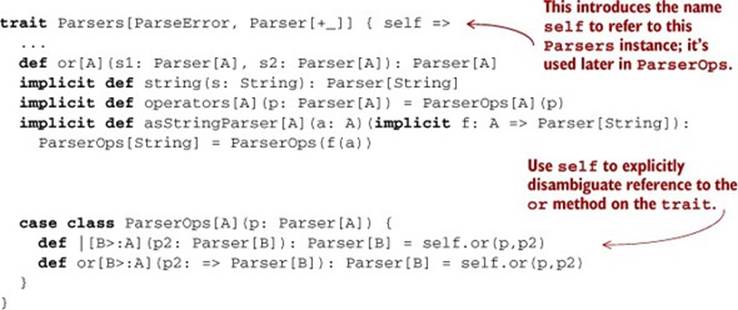
We’ve also made string an implicit conversion and added another implicit asStringParser. With these two functions, Scala will automatically promote a String to a Parser, and we get infix operators for any type that can be converted to a Parser[String]. So given val P: Parsers, we can then import P._ to let us write expressions like "abra" | "cadabra" to create parsers. This will work for all implementations of Parsers. Other binary operators or methods can be added to the body of ParserOps. We’ll follow the discipline of keeping the primary definition directly in Parsers and delegating in ParserOps to this primary definition. See the code for this chapter for more examples. We’ll use the a | b syntax liberally throughout the rest of this chapter to mean or(a,b).
We can now recognize various strings, but we don’t have a way of talking about repetition. For instance, how would we recognize three repetitions of our "abra" | "cadabra" parser? Once again, let’s add a combinator for it:[6]
6 This should remind you of a similar function we wrote in the previous chapter.
def listOfN[A](n: Int, p: Parser[A]): Parser[List[A]]
We made listOfN parametric in the choice of A, since it doesn’t seem like it should care whether we have a Parser[String], a Parser[Char], or some other type of parser. Here are some examples of what we expect from listOfN:
run(listOfN(3, "ab" | "cad"))("ababcad") == Right("ababcad")
run(listOfN(3, "ab" | "cad"))("cadabab") == Right("cadabab")
run(listOfN(3, "ab" | "cad"))("ababab") == Right("ababab")
run(listOfN(3, "ab" | "cad"))("ababcad") == Right("ababcad") run(listOfN(3, "ab" | "cad"))("cadabab") == Right("cadabab") run(listOfN(3, "ab" | "cad"))("ababab") == Right("ababab")
At this point, we’ve just been collecting up required combinators, but we haven’t tried to refine our algebra into a minimal set of primitives, and we haven’t talked much about more general laws. We’ll start doing this next, but rather than give the game away, we’ll ask you to examine a few more simple use cases yourself and try to design a minimal algebra with associated laws. This should be a challenging exercise, but enjoy struggling with it and see what you can come up with.
Here are additional parsing tasks to consider, along with some guiding questions:
· A Parser[Int] that recognizes zero or more 'a' characters, and whose result value is the number of 'a' characters it has seen. For instance, given "aa", the parser results in 2; given "" or "b123" (a string not starting with 'a'), it results in 0; and so on.
· A Parser[Int] that recognizes one or more 'a' characters, and whose result value is the number of 'a' characters it has seen. (Is this defined somehow in terms of the same combinators as the parser for 'a' repeated zero or more times?) The parser should fail when given a string without a starting 'a'. How would you like to handle error reporting in this case? Could the API support giving an explicit message like "Expected one or more 'a'" in the case of failure?
· A parser that recognizes zero or more 'a', followed by one or more 'b', and which results in the pair of counts of characters seen. For instance, given "bbb", we get (0,3), given "aaaab", we get (4,1), and so on.
And additional considerations:
· If we’re trying to parse a sequence of zero or more "a" and are only interested in the number of characters seen, it seems inefficient to have to build up, say, a List[Char] only to throw it away and extract the length. Could something be done about this?
· Are the various forms of repetition primitive in our algebra, or could they be defined in terms of something simpler?
· We introduced a type ParseError earlier, but so far we haven’t chosen any functions for the API of ParseError and our algebra doesn’t have any way of letting the programmer control what errors are reported. This seems like a limitation, given that we’d like meaningful error messages from our parsers. Can you do something about it?
· Does a | b mean the same thing as b | a? This is a choice you get to make. What are the consequences if the answer is yes? What about if the answer is no?
· Does a | (b | c) mean the same thing as (a | b) | c? If yes, is this a primitive law for your algebra, or is it implied by something simpler?
· Try to come up with a set of laws to specify your algebra. You don’t necessarily need the laws to be complete; just write down some laws that you expect should hold for any Parsers implementation.
Spend some time coming up with combinators and possible laws based on this guidance. When you feel stuck or at a good stopping point, then continue by reading the next section, which walks through one possible design.
The advantages of algebraic design
When you design the algebra of a library first, representations for the data types of the algebra don’t matter as much. As long as they support the required laws and functions, you don’t even need to make your representations public.
There’s an idea here that a type is given meaning based on its relationship to other types (which are specified by the set of functions and their laws), rather than its internal representation.[7] This viewpoint is often associated with category theory, a branch of mathematics we’ve mentioned before. See the chapter notes for more on this connection if you’re interested.
7 This sort of viewpoint might also be associated with object-oriented design, although OO hasn’t traditionally placed much emphasis on algebraic laws. Furthermore, a big reason for encapsulation in OO is that objects often have some mutable state, and making this public would allow client code to violate invariants. That concern isn’t relevant in FP.
9.2. A possible algebra
We’ll walk through the discovery of a set of combinators for the parsing tasks mentioned earlier. If you worked through this design task yourself, you likely took a different path and may have ended up with a different set of combinators, which is fine.
First, let’s consider the parser that recognizes zero or more repetitions of the character 'a' and returns the number of characters it has seen. We can start by adding a primitive combinator for it; let’s call it many:
def many[A](p: Parser[A]): Parser[List[A]]
This isn’t exactly what we’re after—we need a Parser[Int] that counts the number of elements. We could change the many combinator to return a Parser[Int], but that feels too specific—undoubtedly there will be occasions where we care about more than just the list length. Better to introduce another combinator that should be familiar by now, map:
def map[A,B](a: Parser[A])(f: A => B): Parser[B]
We can now define our parser like this:
map(many(char('a')))(_.size)
Let’s add map and many as methods in ParserOps, so we can write the same thing with nicer syntax:
val numA: Parser[Int] = char('a').many.map(_.size)
We expect that, for instance, run(numA)("aaa") gives Right(3), and run(numA)("b") gives Right(0).
We have a strong expectation for the behavior of map—it should merely transform the result value if the Parser was successful. No additional input characters should be examined by map, and a failing parser can’t become a successful one via map or vice versa. In general, we expect map to be structure preserving much like we required for Par and Gen. Let’s formalize this by stipulating the now-familiar law:
map(p)(a => a) == p
How should we document this law? We could put it in a documentation comment, but in the preceding chapter we developed a way to make our laws executable. Let’s use that library here.
Listing 9.2. Combining Parser with map
import fpinscala.testing._
trait Parsers[ParseError, Parser[+_]]
...
object Laws {
def equal[A](p1: Parser[A], p2: Parser[A])(in: Gen[String]): Prop =
forAll(in)(s => run(p1)(s)== run(p2)(s))
def mapLaw[A](p: Parser[A])(in: Gen[String]): Prop =
equal(p, p.map(a => a))(in)
}
}
This will come in handy later when we test that our implementation of Parsers behaves as we expect. When we discover more laws later on, you’re encouraged to write them out as actual properties inside the Laws object.[8]
8 Again, see the chapter code for more examples. In the interest of keeping this chapter shorter, we won’t give Prop implementations of all the laws, but that doesn’t mean you shouldn’t write them yourself!
Incidentally, now that we have map, we can actually implement char in terms of string:
def char(c: Char): Parser[Char] =
string(c.toString) map (_.charAt(0))
And similarly another combinator, succeed, can be defined in terms of string and map:
def succeed[A](a: A): Parser[A] =
string("") map (_ => a)
This parser always succeeds with the value a, regardless of the input string (since string("") will always succeed, even if the input is empty). Does this combinator seem familiar to you? We can specify its behavior with a law:
run(succeed(a))(s) == Right(a)
9.2.1. Slicing and nonempty repetition
The combination of many and map certainly lets us express the parsing task of counting the number of 'a' characters, but it seems inefficient to construct a List[Char] only to discard its values and extract its length. It would be nice if we could run a Parser purely to see what portion of the input string it examines. Let’s conjure up a combinator for that purpose:
def slice[A](p: Parser[A]): Parser[String]
We call this combinator slice since we intend for it to return the portion of the input string examined by the parser if successful. As an example, run(slice(('a'|'b') .many))("aaba") results in Right("aaba")—we ignore the list accumulated by many and simply return the portion of the input string matched by the parser.
With slice, our parser that counts 'a' characters can now be written as char('a') .many.slice.map(_.size) (assuming we add an alias for slice to ParserOps). The _.size function here is now referencing the size method on String, which takes constant time, rather than the size method on List, which takes time proportional to the length of the list (and requires us to actually construct the list).
Note that there’s no implementation here yet. We’re still just coming up with our desired interface. But slice does put a constraint on the implementation, namely, that even if the parser p.many.map(_.size) will generate an intermediate list when run, slice(p.many).map(_.size)will not. This is a strong hint that slice is primitive, since it will have to have access to the internal representation of the parser.
Let’s consider the next use case. What if we want to recognize one or more 'a' characters? First, we introduce a new combinator for it, many1:
def many1[A](p: Parser[A]): Parser[List[A]]
It feels like many1 shouldn’t have to be primitive, but should be defined somehow in terms of many. Really, many1(p) is just p followed by many(p). So it seems we need some way of running one parser, followed by another, assuming the first is successful. Let’s add that:
def product[A,B](p: Parser[A], p2: Parser[B]): Parser[(A,B)]
We can add ** and product as methods on ParserOps, where a ** b and a product b both delegate to product(a,b).
Exercise 9.1
![]()
Using product, implement the now-familiar combinator map2 and then use this to implement many1 in terms of many. Note that we could have chosen to make map2 primitive and defined product in terms of map2 as we’ve done in previous chapters. The choice is up to you.
def map2[A,B,C](p: Parser[A], p2: Parser[B])(f: (A,B) => C): Parser[C]
With many1, we can now implement the parser for zero or more 'a' followed by one or more 'b' as follows:
char('a').many.slice.map(_.size) ** char('b').many1.slice.map(_.size)
Exercise 9.2
![]()
Hard: Try coming up with laws to specify the behavior of product.
Now that we have map2, is many really primitive? Let’s think about what many(p) will do. It tries running p, followed by many(p) again, and again, and so on until the attempt to parse p fails. It’ll accumulate the results of all successful runs of p into a list. As soon as p fails, the parser returns the empty List.
Exercise 9.3
![]()
Hard: Before continuing, see if you can define many in terms of or, map2, and succeed.
Exercise 9.4
![]()
Hard: Using map2 and succeed, implement the listOfN combinator from earlier.
def listOfN[A](n: Int, p: Parser[A]): Parser[List[A]]
Now let’s try to implement many. Here’s an implementation in terms of or, map2, and succeed:
def many[A](p: Parser[A]): Parser[List[A]] =
map2(p, many(p))(_ :: _) or succeed(List())
This code looks nice and tidy. We’re using map2 to say that we want p followed by many(p) again, and that we want to combine their results with :: to construct a list of results. Or, if that fails, we want to succeed with the empty list. But there’s a problem with this implementation. Can you spot what it is? We’re calling many recursively in the second argument to map2, which is strict in evaluating its second argument. Consider a simplified program trace of the evaluation of many(p) for some parser p. We’re only showing the expansion of the left side of the or here:
many(p)
map2(p, many(p))(_ :: _)
map2(p, map2(p, many(p))(_ :: _))(_ :: _)
map2(p, map2(p, map2(p, many(p))(_ :: _))(_ :: _))(_ :: _)
...
Because a call to map2 always evaluates its second argument, our many function will never terminate! That’s no good. This indicates that we need to make product and map2 non-strict in their second argument:
def product[A,B](p: Parser[A], p2: => Parser[B]): Parser[(A,B)]
def map2[A,B,C](p: Parser[A], p2: => Parser[B])(
f: (A,B) => C): Parser[C] =
product(p, p2) map (f.tupled)
Exercise 9.5
![]()
We could also deal with non-strictness with a separate combinator like we did in chapter 7. Try this here and make the necessary changes to your existing combinators. What do you think of that approach in this instance?
Now our implementation of many should work fine. Conceptually, product should have been non-strict in its second argument anyway, since if the first Parser fails, the second won’t even be consulted.
We now have good combinators for parsing one thing followed by another, or multiple things of the same kind in succession. But since we’re considering whether combinators should be non-strict, let’s revisit the or combinator from earlier:
def or[A](p1: Parser[A], p2: Parser[A]): Parser[A]
We’ll assume that or is left-biased, meaning it tries p1 on the input, and then tries p2 only if p1 fails.[9] In this case, we ought to make it non-strict in its second argument, which may never even be consulted:
9 This is a design choice. You may wish to think about the consequences of having a version of or that always runs both p1 and p2.
def or[A](p1: Parser[A], p2: => Parser[A]): Parser[A]
9.3. Handling context sensitivity
Let’s take a step back and look at the primitives we have so far:
· string(s) —Recognizes and returns a single String
· slice(p) —Returns the portion of input inspected by p if successful
· succeed(a) —Always succeeds with the value a
· map(p)(f) —Applies the function f to the result of p, if successful
· product(p1,p2) —Sequences two parsers, running p1 and then p2, and returns the pair of their results if both succeed
· or(p1,p2) —Chooses between two parsers, first attempting p1, and then p2 if p1 fails
Using these primitives, we can express repetition and nonempty repetition (many, listOfN, and many1) as well as combinators like char and map2. Would it surprise you if these primitives were sufficient for parsing any context-free grammar, including JSON? Well, they are! We’ll get to writing that JSON parser soon, but what can’t we express yet?
Suppose we want to parse a single digit, like '4', followed by that many 'a' characters (this sort of problem should feel familiar from previous chapters). Examples of valid input are "0", "1a", "2aa", "4aaaa", and so on. This is an example of a context-sensitive grammar. It can’t be expressed with product because our choice of the second parser depends on the result of the first (the second parser depends on its context). We want to run the first parser, and then do a listOfN using the number extracted from the first parser’s result. Can you see why product can’t express this?
This progression might feel familiar to you. In past chapters, we encountered similar expressiveness limitations and dealt with it by introducing a new primitive, flat-Map. Let’s introduce that here (and we’ll add an alias to ParserOps so we can write parsers using for-comprehensions):
def flatMap[A,B](p: Parser[A])(f: A => Parser[B]): Parser[B]
Can you see how this signature implies an ability to sequence parsers where each parser in the chain depends on the output of the previous one?
Exercise 9.6
![]()
Using flatMap and any other combinators, write the context-sensitive parser we couldn’t express earlier. To parse the digits, you can make use of a new primitive, regex, which promotes a regular expression to a Parser.[10] In Scala, a string s can be promoted to a Regex object (which has methods for matching) using s.r, for instance, "[a-zA-Z_][a-zA-Z0-9_]*".r.
10 In theory this isn’t necessary; we could write out "0" | "1" | ... "9" to recognize a single digit, but this isn’t likely to be very efficient.
implicit def regex(r: Regex): Parser[String]
Exercise 9.7
![]()
Implement product and map2 in terms of flatMap.
Exercise 9.8
![]()
map is no longer primitive. Express it in terms of flatMap and/or other combinators.
So it appears we have a new primitive, flatMap, which enables context-sensitive parsing and lets us implement map and map2. This is not the first time flatMap has made an appearance.
We now have an even smaller set of just six primitives: string, regex, slice, succeed, or, and flatMap. But we also have more power than before. With flatMap, instead of the less-general map and product, we can parse not just arbitrary context-free grammars like JSON, but context-sensitive grammars as well, including extremely complicated ones like C++ and PERL!
9.4. Writing a JSON parser
Let’s write that JSON parser now, shall we? We don’t have an implementation of our algebra yet, and we’ve yet to add any combinators for good error reporting, but we can deal with these things later. Our JSON parser doesn’t need to know the internal details of how parsers are represented. We can simply write a function that produces a JSON parser using only the set of primitives we’ve defined and any derived combinators.
That is, for some JSON parse result type (we’ll explain the JSON format and the parse result type shortly), we’ll write a function like this:

This might seem like a peculiar thing to do, since we won’t actually be able to run our parser until we have a concrete implementation of the Parsers interface. But we’ll proceed, because in FP, it’s common to define an algebra and explore its expressiveness without having a concrete implementation. A concrete implementation can tie us down and makes changes to the API more difficult. Especially during the design phase of a library, it can be much easier to refine an algebra without having to commit to any particular implementation, and part of our goal here is to get you comfortable with this style of working.
After this section, we’ll return to the question of adding better error reporting to our parsing API. We can do this without disturbing the overall structure of the API or changing our JSON parser very much. And we’ll also come up with a concrete, runnable representation of our Parser type. Importantly, the JSON parser we’ll implement in this next section will be completely independent of that representation.
9.4.1. The JSON format
If you aren’t already familiar with the JSON format, you may want to read Wikipedia’s description (http://mng.bz/DpNA) and the grammar specification (http://json.org). Here’s an example JSON document:
{
"Company name" : "Microsoft Corporation",
"Ticker" : "MSFT",
"Active" : true,
"Price" : 30.66,
"Shares outstanding" : 8.38e9,
"Related companies" :
[ "HPQ", "IBM", "YHOO", "DELL", "GOOG" ]
}
A value in JSON can be one of several types. An object in JSON is a comma-separated sequence of key-value pairs, wrapped in curly braces ({}). The keys must be strings like "Ticker" or "Price", and the values can be either another object, an array like ["HPQ", "IBM" ... ] that contains further values, or a literal like "MSFT", true, null, or 30.66.
We’ll write a rather dumb parser that simply parses a syntax tree from the document without doing any further processing.[11] We’ll need a representation for a parsed JSON document. Let’s introduce a data type for this:
11 See the chapter notes for discussion of alternate approaches.
trait JSON
object JSON {
case object JNull extends JSON
case class JNumber(get: Double) extends JSON
case class JString(get: String) extends JSON
case class JBool(get: Boolean) extends JSON
case class JArray(get: IndexedSeq[JSON]) extends JSON
case class JObject(get: Map[String, JSON]) extends JSON
}
9.4.2. A JSON parser
Recall that we’ve built up the following set of primitives:
· string(s): Recognizes and returns a single String
· regex(s): Recognizes a regular expression s
· slice(p): Returns the portion of input inspected by p if successful
· succeed(a): Always succeeds with the value a
· flatMap(p)(f): Runs a parser, then uses its result to select a second parser to run in sequence
· or(p1,p2): Chooses between two parsers, first attempting p1, and then p2 if p1 fails
We used these primitives to define a number of combinators like map, map2, many, and many1.
Exercise 9.9
![]()
Hard: At this point, you are going to take over the process. You’ll be creating a Parser[JSON] from scratch using the primitives we’ve defined. You don’t need to worry (yet) about the representation of Parser. As you go, you’ll undoubtedly discover additional combinators and idioms, notice and factor out common patterns, and so on. Use the skills you’ve been developing throughout this book, and have fun! If you get stuck, you can always consult the answers.
Here’s some minimal guidance:
· Any general-purpose combinators you discover can be added to the Parsers trait directly.
· You’ll probably want to introduce combinators that make it easier to parse the tokens of the JSON format (like string literals and numbers). For this you could use the regex primitive we introduced earlier. You could also add a few primitives like letter, digit, whitespace, and so on, for building up your token parsers.
Consult the hints if you’d like more guidance. A full JSON parser is given in the file JSON.scala in the answers.
9.5. Error reporting
So far we haven’t discussed error reporting at all. We’ve focused exclusively on discovering a set of primitives that let us express parsers for different grammars. But besides just parsing a grammar, we want to be able to determine how the parser should respond when given unexpected input.
Even without knowing what an implementation of Parsers will look like, we can reason abstractly about what information is being specified by a set of combinators. None of the combinators we’ve introduced so far say anything about what error message should be reported in the event of failure or what other information a ParseError should contain. Our existing combinators only specify what the grammar is and what to do with the result if successful. If we were to declare ourselves done and move to implementation at this point, we’d have to make some arbitrary decisions about error reporting and error messages that are unlikely to be universally appropriate.
Exercise 9.10
![]()
Hard: If you haven’t already done so, spend some time discovering a nice set of combinators for expressing what errors get reported by a Parser. For each combinator, try to come up with laws specifying what its behavior should be. This is a very open-ended design task. Here are some guiding questions:
· Given the parser "abra".**(" ".many).**("cadabra"), what sort of error would you like to report given the input "abra cAdabra" (note the capital 'A')? Only something like Expected 'a'? Or Expected "cadabra"? What if you wanted to choose a different error message, like "Magic word incorrect, try again!"?
· Given a or b, if a fails on the input, do we always want to run b, or are there cases where we might not want to? If there are such cases, can you think of additional combinators that would allow the programmer to specify when or should consider the second parser?
· How do you want to handle reporting the location of errors?
· Given a or b, if a and b both fail on the input, might we want to support reporting both errors? And do we always want to report both errors, or do we want to give the programmer a way to specify which of the two errors is reported?
We suggest you continue reading once you’re satisfied with your design. The next section works through a possible design in detail.
Combinators specify information
In a typical library design scenario, where we have at least some idea of a concrete representation, we often think of functions in terms of how they will affect this representation. By starting with the algebra first, we’re forced to think differently—we must think of functions in terms of what information they specify to a possible implementation. The signatures determine what information is given to the implementation, and the implementation is free to use this information however it wants as long as it respects any specified laws.
9.5.1. A possible design
Now that you’ve spent some time coming up with some good error-reporting combinators, we’ll work through one possible design. Again, you may have arrived at a different design and that’s totally fine. This is just another opportunity to see a worked design process.
We’ll progressively introduce our error-reporting combinators. To start, let’s introduce an obvious one. None of the primitives so far let us assign an error message to a parser. We can introduce a primitive combinator for this, label:
def label[A](msg: String)(p: Parser[A]): Parser[A]
The intended meaning of label is that if p fails, its ParseError will somehow incorporate msg. What does this mean exactly? Well, we could just assume type ParseError = String and that the returned ParseError will equal the label. But we’d like our parse error to also tell uswhere the problem occurred. Let’s tentatively add this to our algebra:
case class Location(input: String, offset: Int = 0) {
lazy val line = input.slice(0,offset+1).count(_ == '\n') + 1
lazy val col = input.slice(0,offset+1).lastIndexOf('\n') match {
case -1 => offset + 1
case lineStart => offset - lineStart
}
}
def errorLocation(e: ParseError): Location
def errorMessage(e: ParseError): String
We’ve picked a concrete representation for Location here that includes the full input, an offset into this input, and the line and column numbers, which can be computed lazily from the full input and offset. We can now say more precisely what we expect from label. In the event of failure with Left(e), errorMessage(e) will equal the message set by label. This can be specified with a Prop:
def labelLaw[A](p: Parser[A], inputs: SGen[String]): Prop =
forAll(inputs ** Gen.string) { case (input, msg) =>
run(label(msg)(p))(input) match {
case Left(e) => errorMessage(e) == msg
case _ => true
}
}
What about the Location? We’d like for this to be filled in by the Parsers implementation with the location where the error occurred. This notion is still a bit fuzzy—if we have a or b and both parsers fail on the input, which location is reported, and which label(s)? We’ll discuss this in the next section.
9.5.2. Error nesting
Is the label combinator sufficient for all our error-reporting needs? Not quite. Let’s look at an example:

What sort of ParseError would we like to get back from run(p)("abra cAdabra")? (Note the capital A in cAdabra.) The immediate cause is that capital 'A' instead of the expected lowercase 'a'. That error will have a location, and it might be nice to report it somehow. But reportingonly that low-level error wouldn’t be very informative, especially if this were part of a large grammar and we were running the parser on a larger input. We have some more context that would be useful to know—the immediate error occurred in the Parser labeled "second magic word". This is certainly helpful information. Ideally, the error message should tell us that while parsing "second magic word", there was an unexpected capital 'A'. That pinpoints the error and gives us the context needed to understand it. Perhaps the top-level parser (p in this case) might be able to provide an even higher-level description of what the parser was doing when it failed ("parsing magic spell", say), which could also be informative.
So it seems wrong to assume that one level of error reporting will always be sufficient. Let’s therefore provide a way to nest labels:
def scope[A](msg: String)(p: Parser[A]): Parser[A]
Unlike label, scope doesn’t throw away the label(s) attached to p—it merely adds additional information in the event that p fails. Let’s specify what this means exactly. First, we modify the functions that pull information out of a ParseError.
Rather than containing just a single Location and String message, we should get a List[(Location,String)]:
case class ParseError(stack: List[(Location,String)])
This is a stack of error messages indicating what the Parser was doing when it failed. We can now specify what scope does—if run(p)(s) is Left(e1), then run(scope(msg) (p)) is Left(e2), where e2.stack.head will be msg and e2.stack.tail will be e1.
We can write helper functions later to make constructing and manipulating ParseError values more convenient, and to format them nicely for human consumption. For now, we just want to make sure it contains all the relevant information for error reporting, and it seems like ParseErrorwill be sufficient for most purposes. Let’s pick this as our concrete representation and remove the abstract type parameter from Parsers:
trait Parsers[Parser[+_]] {
def run[A](p: Parser[A])(input: String): Either[ParseError,A]
...
}
Now we’re giving the Parsers implementation all the information it needs to construct nice, hierarchical errors if it chooses. As users of the Parsers library, we’ll judiciously sprinkle our grammar with label and scope calls that the Parsers implementation can use when constructing parse errors. Note that it would be perfectly reasonable for implementations of Parsers to not use the full power of ParseError and retain only basic information about the cause and location of errors.
9.5.3. Controlling branching and backtracking
There’s one last concern regarding error reporting that we need to address. As we just discussed, when we have an error that occurs inside an or combinator, we need some way of determining which error(s) to report. We don’t want to only have a global convention for this; we sometimes want to allow the programmer to control this choice. Let’s look at a more concrete motivating example:
val spaces = " ".many
val p1 = scope("magic spell") {
"abra" ** spaces ** "cadabra"
}
val p2 = scope("gibberish") {
"abba" ** spaces ** "babba"
}
val p = p1 or p2
What ParseError would we like to get back from run(p)("abra cAdabra")? (Again, note the capital A in cAdabra.) Both branches of the or will produce errors on the input. The "gibberish"-labeled parser will report an error due to expecting the first word to be "abba", and the"magic spell" parser will report an error due to the accidental capitalization in "cAdabra". Which of these errors do we want to report back to the user?
In this instance, we happen to want the "magic spell" parse error—after successfully parsing the "abra" word, we’re committed to the "magic spell" branch of the or, which means if we encounter a parse error, we don’t examine the next branch of the or. In other instances, we may want to allow the parser to consider the next branch of the or.
So it appears we need a primitive for letting the programmer indicate when to commit to a particular parsing branch. Recall that we loosely assigned p1 or p2 to mean try running p1 on the input, and then try running p2 on the same input if p1 fails. We can change its meaning to try running p1 on the input, and if it fails in an uncommitted state, try running p2 on the same input; otherwise, report the failure. This is useful for more than just providing good error messages—it also improves efficiency by letting the implementation avoid examining lots of possible parsing branches.
One common solution to this problem is to have all parsers commit by default if they examine at least one character to produce a result.[12] We then introduce a combinator, attempt, which delays committing to a parse:
12 See the chapter notes for more discussion of this.
def attempt[A](p: Parser[A]): Parser[A]
It should satisfy something like this:[13]
13 This is not quite an equality. Even though we want to run p2 if the attempted parser fails, we may want p2 to somehow incorporate the errors from both branches if it fails.
attempt(p flatMap (_ => fail)) or p2 == p2
Here fail is a parser that always fails (we could introduce this as a primitive combinator if we like). That is, even if p fails midway through examining the input, attempt reverts the commit to that parse and allows p2 to be run. The attempt combinator can be used whenever there’s ambiguity in the grammar and multiple tokens may have to be examined before the ambiguity can be resolved and parsing can commit to a single branch. As an example, we might write this:
(attempt("abra" ** spaces ** "abra") ** "cadabra") or (
"abra" ** spaces "cadabra!")
Suppose this parser is run on "abra cadabra!"—after parsing the first "abra", we don’t know whether to expect another "abra" (the first branch) or "cadabra!" (the second branch). By wrapping an attempt around "abra" ** spaces ** "abra", we allow the second branch to be considered up until we’ve finished parsing the second "abra", at which point we commit to that branch.
Exercise 9.11
![]()
Can you think of any other primitives that might be useful for letting the programmer specify what error(s) in an or chain get reported?
Note that we still haven’t written an implementation of our algebra! But this exercise has been more about making sure our combinators provide a way for users of our library to convey the right information to the implementation. It’s up to the implementation to figure out how to use this information in a way that satisfies the laws we’ve stipulated.
9.6. Implementing the algebra
By this point, we’ve fleshed out our algebra and defined a Parser[JSON] in terms of it.[14] Aren’t you curious to try running it?
14 You may want to revisit your parser to make use of some of the error-reporting combinators we just discussed in the previous section.
Let’s again recall our set of primitives:
· string(s) —Recognizes and returns a single String
· regex(s) —Recognizes a regular expression s
· slice(p) —Returns the portion of input inspected by p if successful
· label(e)(p) —In the event of failure, replaces the assigned message with e
· scope(e)(p) —In the event of failure, adds e to the error stack returned by p
· flatMap(p)(f) —Runs a parser, and then uses its result to select a second parser to run in sequence
· attempt(p) —Delays committing to p until after it succeeds
· or(p1,p2) —Chooses between two parsers, first attempting p1, and then p2 if p1 fails in an uncommitted state on the input
Exercise 9.12
![]()
Hard: In the next section, we’ll work through a representation for Parser and implement the Parsers interface using this representation. But before we do that, try to come up with some ideas on your own. This is a very open-ended design task, but the algebra we’ve designed places strong constraints on possible representations. You should be able to come up with a simple, purely functional representation of Parser that can be used to implement the Parsers interface.[15]
15 Note that if you try running your JSON parser once you have an implementation of Parsers, you may get a stack overflow error. See the end of the next section for a discussion of this.
Your code will likely look something like this:
class MyParser[+A](...) { ... }
object MyParsers extends Parsers[MyParser] {
// implementations of primitives go here
}
Replace MyParser with whatever data type you use for representing your parsers. When you have something you’re satisfied with, get stuck, or want some more ideas, keep reading.
9.6.1. One possible implementation
We’re now going to discuss an implementation of Parsers. Our parsing algebra supports a lot of features. Rather than jumping right to the final representation of Parser, we’ll build it up gradually by inspecting the primitives of the algebra and reasoning about the information that will be required to support each one.
Let’s begin with the string combinator:
def string(s: String): Parser[A]
We know we need to support the function run:
def run[A](p: Parser[A])(input: String): Either[ParseError,A]
As a first guess, we can assume that our Parser is simply the implementation of the run function:
type Parser[+A] = String => Either[ParseError,A]
We could use this to implement the string primitive:

The else branch has to build up a ParseError. These are a little inconvenient to construct right now, so we’ve introduced a helper function, toError, on Location:
def toError(msg: String): ParseError =
ParseError(List((this, msg)))
9.6.2. Sequencing parsers
So far, so good. We have a representation for Parser that at least supports string. Let’s move on to sequencing of parsers. Unfortunately, to represent a parser like "abra" ** "cadabra", our existing representation isn’t going to suffice. If the parse of "abra" is successful, then we want to consider those characters consumed and run the "cadabra" parser on the remaining characters. So in order to support sequencing, we require a way of letting a Parser indicate how many characters it consumed. Capturing this is pretty easy:[16]
16 Recall that Location contains the full input string and an offset into this string.

We introduced a new type here, Result, rather than just using Either. In the event of success, we return a value of type A as well as the number of characters of input consumed, which the caller can use to update the Location state.[17] This type is starting to get at the essence of what aParser is—it’s a kind of state action that can fail, similar to what we built in chapter 6. It receives an input state, and if successful, returns a value as well as enough information to control how the state should be updated.
17 Note that returning an (A,Location) would give Parser the ability to change the input stored in the Location. That’s granting it too much power!
This understanding—that a Parser is just a state action—gives us a way of framing a representation that supports all the fancy combinators and laws we’ve stipulated. We simply consider what each primitive requires our state type to track (just a Location may not be sufficient), and work through the details of how each combinator transforms this state.
Exercise 9.13
![]()
Implement string, regex, succeed, and slice for this initial representation of Parser. Note that slice is less efficient than it could be, since it must still construct a value only to discard it. We’ll return to this later.
9.6.3. Labeling parsers
Moving down our list of primitives, let’s look at scope next. In the event of failure, we want to push a new message onto the ParseError stack. Let’s introduce a helper function for this on ParseError. We’ll call it push:[18]
18 The copy method comes for free with any case class. It returns a copy of the object, but with one or more attributes modified. If no new value is specified for a field, it will have the same value as in the original object. Behind the scenes, this just uses the ordinary mechanism for default arguments in Scala.
def push(loc: Location, msg: String): ParseError =
copy(stack = (loc,msg) :: stack)
With this we can implement scope:

The function mapError is defined on Result—it just applies a function to the failing case:
def mapError(f: ParseError => ParseError): Result[A] = this match {
case Failure(e) => Failure(f(e))
case _ => this
}
Because we push onto the stack after the inner parser has returned, the bottom of the stack will have more detailed messages that occurred later in parsing. For example, if scope(msg1)(a ** scope(msg2)(b)) fails while parsing b, the first error on the stack will be msg1, followed by whatever errors were generated by a, then msg2, and finally errors generated by b.
We can implement label similarly, but instead of pushing onto the error stack, it replaces what’s already there. We can write this again using mapError:

We added a helper function to ParseError, also named label. We’ll make a design decision that label trims the error stack, cutting off more detailed messages from inner scopes, using only the most recent location from the bottom of the stack:

Exercise 9.14
![]()
Revise your implementation of string to use scope and/or label to provide a meaningful error message in the event of an error.
9.6.4. Failover and backtracking
Let’s now consider or and attempt. Recall what we specified for the expected behavior of or: it should run the first parser, and if that fails in an uncommitted state, it should run the second parser on the same input. We said that consuming at least one character should result in a committed parse, and that attempt(p) converts committed failures of p to uncommitted failures.
We can support the behavior we want by adding one more piece of information to the Failure case of Result—a Boolean value indicating whether the parser failed in a committed state:
case class Failure(get: ParseError,
isCommitted: Boolean) extends Result[Nothing]
The implementation of attempt just cancels the commitment of any failures that occur. It uses a helper function, uncommit, which we can define on Result:
def attempt[A](p: Parser[A]): Parser[A] =
s => p(s).uncommit
def uncommit: Result[A] = this match {
case Failure(e,true) => Failure(e,false)
case _ => this
}
Now the implementation of or can simply check the isCommitted flag before running the second parser. In the parser x or y, if x succeeds, then the whole thing succeeds. If x fails in a committed state, we fail early and skip running y. Otherwise, if x fails in an uncommitted state, we runy and ignore the result of x:

9.6.5. Context-sensitive parsing
Now for the final primitive in our list, flatMap. Recall that flatMap enables context-sensitive parsers by allowing the selection of a second parser to depend on the result of the first parser. The implementation is simple—we advance the location before calling the second parser. Again we use a helper function, advanceBy, on Location. There is one subtlety—if the first parser consumes any characters, we ensure that the second parser is committed, using a helper function, addCommit, on ParseError.
Listing 9.3. Using addCommit to make sure our parser is committed

advanceBy has the obvious implementation. We simply increment the offset:
def advanceBy(n: Int): Location =
copy(offset = offset+n)
Likewise, addCommit, defined on ParseError, is straightforward:
def addCommit(isCommitted: Boolean): Result[A] = this match {
case Failure(e,c) => Failure(e, c || isCommitted)
case _=> this
}
And finally, advanceSuccess increments the number of consumed characters of a successful result. We want the total number of characters consumed by flatMap to be the sum of the consumed characters of the parser f and the parser produced by g. We use advanceSuccess on the result of g to ensure this:

Exercise 9.15
![]()
Implement the rest of the primitives, including run, using this representation of Parser, and try running your JSON parser on various inputs.[19]
19 You’ll find, unfortunately, that it causes stack overflow for large inputs (for instance, [1,2,3,...10000]). One simple solution to this is to provide a specialized implementation of many that avoids using a stack frame for each element of the list being built up. So long as any combinators that do repetition are defined in terms of many (which they all can be), this solves the problem. See the answers for discussion of more general approaches.
Exercise 9.16
![]()
Come up with a nice way of formatting a ParseError for human consumption. There are a lot of choices to make, but a key insight is that we typically want to combine or group labels attached to the same location when presenting the error as a String for display.
Exercise 9.17
![]()
Hard: The slice combinator is still less efficient than it could be. For instance, many(char('a')).slice will still build up a List[Char], only to discard it. Can you think of a way of modifying the Parser representation to make slicing more efficient?
Exercise 9.18
![]()
Some information is lost when we combine parsers with the or combinator. If both parsers fail, we’re only keeping the errors from the second parser. But we might want to show both error messages, or choose the error from whichever branch got furthest without failing. Change the representation of ParseError to keep track of errors that occurred in other branches of the parser.
9.7. Summary
In this chapter, we introduced algebraic design, an approach to writing combinator libraries, and we used it to design a parser library and to implement a JSON parser. Along the way, we discovered a number of combinators similar to what we saw in previous chapters, and these were again related by familiar laws. In part 3, we’ll finally understand the nature of the connection between these libraries and learn how to abstract over their common structure.
This is the final chapter in part 2. We hope you’ve come away from these chapters with a basic sense of how functional design can proceed, and more importantly, we hope these chapters have motivated you to try your hand at designing your own functional libraries, for whatever domains interest you. Functional design isn’t something reserved only for experts—it should be part of the day-to-day work done by functional programmers at all levels of experience. Before you start on part 3, we encourage you to venture beyond this book, write some more functional code, and design some of your own libraries. Have fun, enjoy struggling with design problems that come up, and see what you discover. When you come back, a universe of patterns and abstractions awaits in part 3.