Functional Programming in Scala (2015)
Part 3. Common structures in functional design
We’ve now written a number of libraries using the principles of functional design. In part 2, we saw these principles applied to a few concrete problem domains. By now you should have a good grasp of how to approach a programming problem in your own work while striving for compositionality and algebraic reasoning.
Part 3 takes a much wider perspective. We’ll look at the common patterns that arise in functional programming. In part 2, we experimented with various libraries that provided concrete solutions to real-world problems, and now we want to integrate what we’ve learned from our experiments into abstract theories that describe the common structure among those libraries.
This kind of abstraction has a direct practical benefit: the elimination of duplicate code. We can capture abstractions as classes, interfaces, and functions that we can refer to in our actual programs. But the primary benefit is conceptual integration. When we recognize common structure among different solutions in different contexts, we unite all of those instances of the structure under a single definition and give it a name. As you gain experience with this, you can look at the general shape of a problem and say, for example: “That looks like a monad!” You’re then already far along in finding the shape of the solution. A secondary benefit is that if other people have developed the same kind of vocabulary, you can communicate your designs to them with extraordinary efficiency.
Part 3 won’t be a sequence of meandering journeys in the style of part 2. Instead, we’ll begin each chapter by introducing an abstract concept, give its definition, and then tie it back to what we’ve seen already. The primary goal will be to train you in recognizing patterns when designing your own libraries, and to write code that takes advantage of such patterns.
Chapter 10. Monoids
By the end of part 2, we were getting comfortable with considering data types in terms of their algebras—that is, the operations they support and the laws that govern those operations. Hopefully you will have noticed that the algebras of very different data types tend to share certain patterns in common. In this chapter, we’ll begin identifying these patterns and taking advantage of them.
This chapter will be our first introduction to purely algebraic structures. We’ll consider a simple structure, the monoid,[1] which is defined only by its algebra. Other than satisfying the same laws, instances of the monoid interface may have little or nothing to do with one another. Nonetheless, we’ll see how this algebraic structure is often all we need to write useful, polymorphic functions.
1 The name monoid comes from mathematics. In category theory, it means a category with one object. This mathematical connection isn’t important for our purposes in this chapter, but see the chapter notes for more information.
We choose to start with monoids because they’re simple, ubiquitous, and useful. Monoids come up all the time in everyday programming, whether we’re aware of them or not. Working with lists, concatenating strings, or accumulating the results of a loop can often be phrased in terms of monoids. We’ll see how monoids are useful in two ways: they facilitate parallel computation by giving us the freedom to break our problem into chunks that can be computed in parallel; and they can be composed to assemble complex calculations from simpler pieces.
10.1. What is a monoid?
Let’s consider the algebra of string concatenation. We can add "foo" + "bar" to get "foobar", and the empty string is an identity element for that operation. That is, if we say (s + "") or ("" + s), the result is always s. Furthermore, if we combine three strings by saying (r + s + t), the operation is associative—it doesn’t matter whether we parenthesize it: ((r + s) + t) or (r + (s + t)).
The exact same rules govern integer addition. It’s associative, since (x + y) + z is always equal to x + (y + z), and it has an identity element, 0, which “does nothing” when added to another integer. Ditto for multiplication, whose identity element is 1.
The Boolean operators && and || are likewise associative, and they have identity elements true and false, respectively.
These are just a few simple examples, but algebras like this are virtually everywhere. The term for this kind of algebra is monoid. The laws of associativity and identity are collectively called the monoid laws. A monoid consists of the following:
· Some type A
· An associative binary operation, op, that takes two values of type A and combines them into one: op(op(x,y), z) == op(x, op(y,z)) for any choice of x: A, y: A, z: A
· A value, zero: A, that is an identity for that operation: op(x, zero) == x and op(zero, x) == x for any x: A
We can express this with a Scala trait:
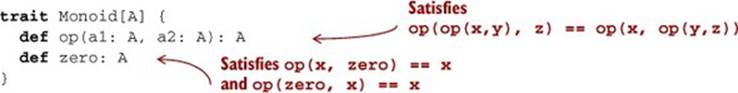
An example instance of this trait is the String monoid:
val stringMonoid = new Monoid[String] {
def op(a1: String, a2: String) = a1 + a2
val zero = ""
}
List concatenation also forms a monoid:
def listMonoid[A] = new Monoid[List[A]] {
def op(a1: List[A], a2: List[A]) = a1 ++ a2
val zero = Nil
}
The purely abstract nature of an algebraic structure
Notice that other than satisfying the monoid laws, the various Monoid instances don’t have much to do with each other. The answer to the question “What is a monoid?” is simply that a monoid is a type, together with the monoid operations and a set of laws. A monoid is the algebra, and nothing more. Of course, you may build some other intuition by considering the various concrete instances, but this intuition is necessarily imprecise and nothing guarantees that all monoids you encounter will match your intuition!
Exercise 10.1
![]()
Give Monoid instances for integer addition and multiplication as well as the Boolean operators.
val intAddition: Monoid[Int]
val intMultiplication: Monoid[Int]
val booleanOr: Monoid[Boolean]
val booleanAnd: Monoid[Boolean]
Exercise 10.2
![]()
Give a Monoid instance for combining Option values.
def optionMonoid[A]: Monoid[Option[A]]
Exercise 10.3
![]()
A function having the same argument and return type is sometimes called an endofunction.[2] Write a monoid for endofunctions.
2 The Greek prefix endo- means within, in the sense that an endofunction’s codomain is within its domain.
def endoMonoid[A]: Monoid[A => A]
Exercise 10.4
![]()
Use the property-based testing framework we developed in part 2 to implement a property for the monoid laws. Use your property to test the monoids we’ve written.
def monoidLaws[A](m: Monoid[A], gen: Gen[A]): Prop
Having versus being a monoid
There is a slight terminology mismatch between programmers and mathematicians when they talk about a type being a monoid versus having a monoid instance. As a programmer, it’s tempting to think of the instance of type Monoid[A] as being a monoid. But that’s not accurate terminology. The monoid is actually both things—the type together with the instance satisfying the laws. It’s more accurate to say that the type A forms a monoid under the operations defined by the Monoid[A] instance. Less precisely, we might say that “type A is a monoid,” or even that “type A is monoidal.” In any case, the Monoid[A] instance is simply evidence of this fact.
This is much the same as saying that the page or screen you’re reading “forms a rectangle” or “is rectangular.” It’s less accurate to say that it “is a rectangle” (although that still makes sense), but to say that it “has a rectangle” would be strange.
Just what is a monoid, then? It’s simply a type A and an implementation of Monoid[A] that satisfies the laws. Stated tersely, a monoid is a type together with a binary operation (op) over that type, satisfying associativity and having an identity element (zero).
What does this buy us? Just like any abstraction, a monoid is useful to the extent that we can write useful generic code assuming only the capabilities provided by the abstraction. Can we write any interesting programs, knowing nothing about a type other than that it forms a monoid? Absolutely! Let’s look at some examples.
10.2. Folding lists with monoids
Monoids have an intimate connection with lists. If you look at the signatures of fold-Left and foldRight on List, you might notice something about the argument types:
def foldRight[B](z: B)(f: (A, B) => B): B
def foldLeft[B](z: B)(f: (B, A) => B): B
What happens when A and B are the same type?
def foldRight(z: A)(f: (A, A) => A): A
def foldLeft(z: A)(f: (A, A) => A): A
The components of a monoid fit these argument types like a glove. So if we had a list of Strings, we could simply pass the op and zero of the stringMonoid in order to reduce the list with the monoid and concatenate all the strings:
scala> val words = List("Hic", "Est", "Index")
words: List[String] = List(Hic, Est, Index)
scala> val s = words.foldRight(stringMonoid.zero)(stringMonoid.op)
s: String = "HicEstIndex"
scala> val t = words.foldLeft(stringMonoid.zero)(stringMonoid.op)
t: String = "HicEstIndex"
Note that it doesn’t matter if we choose foldLeft or foldRight when folding with a monoid;[3] we should get the same result. This is precisely because the laws of associativity and identity hold. A left fold associates operations to the left, whereas a right fold associates to the right, with the identity element on the left and right respectively:
3 Given that both foldLeft and foldRight have tail-recursive implementations.
words.foldLeft("")(_ + _) == (("" + "Hic") + "Est") + "Index"
words.foldRight("")(_ + _) == "Hic" + ("Est" + ("Index" + ""))
We can write a general function concatenate that folds a list with a monoid:
def concatenate[A](as: List[A], m: Monoid[A]): A =
as.foldLeft(m.zero)(m.op)
But what if our list has an element type that doesn’t have a Monoid instance? Well, we can always map over the list to turn it into a type that does:
def foldMap[A,B](as: List[A], m: Monoid[B])(f: A => B): B
Exercise 10.5
![]()
Implement foldMap.
Exercise 10.6
![]()
Hard: The foldMap function can be implemented using either foldLeft or fold-Right. But you can also write foldLeft and foldRight using foldMap! Try it.
10.3. Associativity and parallelism
The fact that a monoid’s operation is associative means we can choose how we fold a data structure like a list. We’ve already seen that operations can be associated to the left or right to reduce a list sequentially with foldLeft or foldRight. But if we have a monoid, we can reduce a list using a balanced fold, which can be more efficient for some operations and also allows for parallelism.
As an example, suppose we have a sequence a, b, c, d that we’d like to reduce using some monoid. Folding to the right, the combination of a, b, c, and d would look like this:
op(a, op(b, op(c, d)))
Folding to the left would look like this:
op(op(op(a, b), c), d)
But a balanced fold looks like this:
op(op(a, b), op(c, d))
Note that the balanced fold allows for parallelism, because the two inner op calls are independent and can be run simultaneously. But beyond that, the more balanced tree structure can be more efficient in cases where the cost of each op is proportional to the size of its arguments. For instance, consider the runtime performance of this expression:
List("lorem", "ipsum", "dolor", "sit").foldLeft("")(_ + _)
At every step of the fold, we’re allocating the full intermediate String only to discard it and allocate a larger string in the next step. Recall that String values are immutable, and that evaluating a + b for strings a and b requires allocating a fresh character array and copying both a and binto this new array. It takes time proportional to a.length + b.length.
Here’s a trace of the preceding expression being evaluated:
List("lorem", ipsum", "dolor", "sit").foldLeft("")(_ + _)
List("ipsum", "dolor", "sit").foldLeft("lorem")(_ + _)
List("dolor", "sit").foldLeft("loremipsum")(_ + _)
List("sit").foldLeft("loremipsumdolor")(_ + _)
List().foldLeft("loremipsumdolorsit")(_ + _)
"loremipsumdolorsit"
Note the intermediate strings being created and then immediately discarded. A more efficient strategy would be to combine the sequence by halves, which we call a balanced fold—we first construct "loremipsum" and "dolorsit", and then add those together.
Exercise 10.7
![]()
Implement a foldMap for IndexedSeq.[4] Your implementation should use the strategy of splitting the sequence in two, recursively processing each half, and then adding the answers together with the monoid.
4 Recall that IndexedSeq is the interface for immutable data structures supporting efficient random access. It also has efficient splitAt and length methods.
def foldMapV[A,B](v: IndexedSeq[A], m: Monoid[B])(f: A => B): B
Exercise 10.8
![]()
Hard: Also implement a parallel version of foldMap using the library we developed in chapter 7. Hint: Implement par, a combinator to promote Monoid[A] to a Monoid [Par[A]],[5] and then use this to implement parFoldMap.
5 The ability to “lift” a Monoid into the Par context is something we’ll discuss more generally in chapters 11 and 12.
import fpinscala.parallelism.Nonblocking._
def par[A](m: Monoid[A]): Monoid[Par[A]]
def parFoldMap[A,B](v: IndexedSeq[A], m: Monoid[B])(f: A => B): Par[B]
Exercise 10.9
![]()
Hard: Use foldMap to detect whether a given IndexedSeq[Int] is ordered. You’ll need to come up with a creative Monoid.
10.4. Example: Parallel parsing
As a nontrivial use case, let’s say that we wanted to count the number of words in a String. This is a fairly simple parsing problem. We could scan the string character by character, looking for whitespace and counting up the number of runs of consecutive nonwhitespace characters. Parsing sequentially like that, the parser state could be as simple as tracking whether the last character seen was a whitespace.
But imagine doing this not for just a short string, but an enormous text file, possibly too big to fit in memory on a single machine. It would be nice if we could work with chunks of the file in parallel. The strategy would be to split the file into manageable chunks, process several chunks in parallel, and then combine the results. In that case, the parser state needs to be slightly more complicated, and we need to be able to combine intermediate results regardless of whether the section we’re looking at is at the beginning, middle, or end of the file. In other words, we want the combining operation to be associative.
To keep things simple and concrete, let’s consider a short string and pretend it’s a large file:
"lorem ipsum dolor sit amet, "
If we split this string roughly in half, we might split it in the middle of a word. In the case of our string, that would yield "lorem ipsum do" and "lor sit amet, ". When we add up the results of counting the words in these strings, we want to avoid double-counting the word dolor. Clearly, just counting the words as an Int isn’t sufficient. We need to find a data structure that can handle partial results like the half words do and lor, and can track the complete words seen so far, like ipsum, sit, and amet.
The partial result of the word count could be represented by an algebraic data type:
sealed trait WC
case class Stub(chars: String) extends WC
case class Part(lStub: String, words: Int, rStub: String) extends WC
A Stub is the simplest case, where we haven’t seen any complete words yet. But a Part keeps the number of complete words we’ve seen so far, in words. The value lStub holds any partial word we’ve seen to the left of those words, and rStub holds any partial word on the right.
For example, counting over the string "lorem ipsum do" would result in Part ("lorem", 1, "do") since there’s one certainly complete word, "ipsum". And since there’s no whitespace to the left of lorem or right of do, we can’t be sure if they’re complete words, so we don’t count them yet. Counting over "lor sit amet, " would result in Part("lor", 2, "").
Exercise 10.10
![]()
Write a monoid instance for WC and make sure that it meets the monoid laws.
val wcMonoid: Monoid[WC]
Exercise 10.11
![]()
Use the WC monoid to implement a function that counts words in a String by recursively splitting it into substrings and counting the words in those substrings.
Monoid homomorphisms
If you have your law-discovering cap on while reading this chapter, you may notice that there’s a law that holds for some functions between monoids. Take the String concatenation monoid and the integer addition monoid. If you take the lengths of two strings and add them up, it’s the same as taking the length of the concatenation of those two strings:
"foo".length + "bar".length == ("foo" + "bar").length
Here, length is a function from String to Int that preserves the monoid structure. Such a function is called a monoid homomorphism.[6] A monoid homomorphism f between monoids M and N obeys the following general law for all values x and y:
6 Homomorphism comes from Greek, homo meaning “same” and morphe meaning “shape.”
M.op(f(x), f(y)) == f(N.op(x, y))
The same law should hold for the homomorphism from String to WC in the present exercise.
This property can be useful when designing your own libraries. If two types that your library uses are monoids, and there exist functions between them, it’s a good idea to think about whether those functions are expected to preserve the monoid structure and to check the monoid homomorphism law with automated tests.
Sometimes there will be a homomorphism in both directions between two monoids. If they satisfy a monoid isomorphism (iso- meaning equal), we say that the two monoids are isomorphic. A monoid isomorphism between M and N has two homomorphisms f and g, where both f andThen gand g andThen f are an identity function.
For example, the String and List[Char] monoids with concatenation are isomorphic. The two Boolean monoids (false, ||) and (true, &&) are also isomorphic, via the ! (negation) function.
10.5. Foldable data structures
In chapter 3, we implemented the data structures List and Tree, both of which could be folded. In chapter 5, we wrote Stream, a lazy structure that also can be folded much like a List can, and now we’ve just written a fold for IndexedSeq.
When we’re writing code that needs to process data contained in one of these structures, we often don’t care about the shape of the structure (whether it’s a tree or a list), or whether it’s lazy or not, or provides efficient random access, and so forth.
For example, if we have a structure full of integers and want to calculate their sum, we can use foldRight:
ints.foldRight(0)(_ + _)
Looking at just this code snippet, we shouldn’t have to care about the type of ints. It could be a Vector, a Stream, or a List, or anything at all with a foldRight method. We can capture this commonality in a trait:
trait Foldable[F[_]] {
def foldRight[A,B](as: F[A])(z: B)(f: (A,B) => B): B
def foldLeft[A,B](as: F[A])(z: B)(f: (B,A) => B): B
def foldMap[A,B](as: F[A])(f: A => B)(mb: Monoid[B]): B
def concatenate[A](as: F[A])(m: Monoid[A]): A =
foldLeft(as)(m.zero)(m.op)
}
Here we’re abstracting over a type constructor F, much like we did with the Parser type in the previous chapter. We write it as F[_], where the underscore indicates that F is not a type but a type constructor that takes one type argument. Just like functions that take other functions as arguments are called higher-order functions, something like Foldable is a higher-order type constructor or a higher-kinded type.[7]
7 Just like values and functions have types, types and type constructors have kinds. Scala uses kinds to track how many type arguments a type constructor takes, whether it’s co- or contravariant in those arguments, and what the kinds of those arguments are.
Exercise 10.12
![]()
Implement Foldable[List], Foldable[IndexedSeq], and Foldable[Stream]. Remember that foldRight, foldLeft, and foldMap can all be implemented in terms of each other, but that might not be the most efficient implementation.
Exercise 10.13
![]()
Recall the binary Tree data type from chapter 3. Implement a Foldable instance for it.
sealed trait Tree[+A]
case object Leaf[A](value: A) extends Tree[A]
case class Branch[A](left: Tree[A], right: Tree[A]) extends Tree[A]
Exercise 10.14
![]()
Write a Foldable[Option] instance.
Exercise 10.15
![]()
Any Foldable structure can be turned into a List. Write this conversion in a generic way:
def toList[A](fa: F[A]): List[A]
10.6. Composing monoids
The Monoid abstraction in itself is not all that compelling, and with the generalized foldMap it’s only slightly more interesting. The real power of monoids comes from the fact that they compose.
This means, for example, that if types A and B are monoids, then the tuple type (A, B) is also a monoid (called their product).
Exercise 10.16
![]()
Prove it. Notice that your implementation of op is obviously associative so long as A.op and B.op are both associative.
def productMonoid[A,B](A: Monoid[A], B: Monoid[B]): Monoid[(A,B)]
10.6.1. Assembling more complex monoids
Some data structures form interesting monoids as long as the types of the elements they contain also form monoids. For instance, there’s a monoid for merging key-value Maps, as long as the value type is a monoid.
Listing 10.1. Merging key-value Maps
def mapMergeMonoid[K,V](V: Monoid[V]): Monoid[Map[K, V]] =
new Monoid[Map[K, V]] {
def zero = Map[K,V]()
def op(a: Map[K, V], b: Map[K, V]) =
(a.keySet ++ b.keySet).foldLeft(zero) { (acc,k) =>
acc.updated(k, V.op(a.getOrElse(k, V.zero),
b.getOrElse(k, V.zero)))
}
}
Using this simple combinator, we can assemble more complex monoids fairly easily:
scala> val M: Monoid[Map[String, Map[String, Int]]] =
| mapMergeMonoid(mapMergeMonoid(intAddition))
M: Monoid[Map[String, Map[String, Int]]] = $anon$1@21dfac82
This allows us to combine nested expressions using the monoid, with no additional programming:
scala> val m1 = Map("o1" -> Map("i1" -> 1, "i2" -> 2))
m1: Map[String,Map[String,Int]] = Map(o1 -> Map(i1 -> 1, i2 -> 2))
scala> val m2 = Map("o1" -> Map("i2" -> 3))
m2: Map[String,Map[String,Int]] = Map(o1 -> Map(i2 -> 3))
scala> val m3 = M.op(m1, m2)
m3: Map[String,Map[String,Int]] = Map(o1 -> Map(i1 -> 1, i2 -> 5))
Exercise 10.17
![]()
Write a monoid instance for functions whose results are monoids.
def functionMonoid[A,B](B: Monoid[B]): Monoid[A => B]
Exercise 10.18
![]()
A bag is like a set, except that it’s represented by a map that contains one entry per element with that element as the key, and the value under that key is the number of times the element appears in the bag. For example:
scala> bag(Vector("a", "rose", "is", "a", "rose"))
res0: Map[String,Int] = Map(a -> 2, rose -> 2, is -> 1)
Use monoids to compute a “bag” from an IndexedSeq.
def bag[A](as: IndexedSeq[A]): Map[A, Int]
10.6.2. Using composed monoids to fuse traversals
The fact that multiple monoids can be composed into one means that we can perform multiple calculations simultaneously when folding a data structure. For example, we can take the length and sum of a list at the same time in order to calculate the mean:
scala> val m = productMonoid(intAddition, intAddition)
m: Monoid[(Int, Int)] = $anon$1@8ff557a
scala> val p = listFoldable.foldMap(List(1,2,3,4))(a => (1, a))(m)
p: (Int, Int) = (4, 10)
scala> val mean = p._1 / p._2.toDouble
mean: Double = 2.5
It can be tedious to assemble monoids by hand using productMonoid and foldMap. Part of the problem is that we’re building up the Monoid separately from the mapping function of foldMap, and we must manually keep these “aligned” as we did here. But we can create a combinator library that makes it much more convenient to assemble these composed monoids and define complex computations that may be parallelized and run in a single pass. Such a library is beyond the scope of this chapter, but see the chapter notes for a brief discussion and links to further material.
10.7. Summary
Our goal in part 3 is to get you accustomed to working with more abstract structures, and to develop the ability to recognize them. In this chapter, we introduced one of the simplest purely algebraic abstractions, the monoid. When you start looking for it, you’ll find ample opportunity to exploit the monoidal structure of your own libraries. The associative property enables folding any Foldable data type and gives the flexibility of doing so in parallel. Monoids are also compositional, and you can use them to assemble folds in a declarative and reusable way.
Monoid has been our first purely abstract algebra, defined only in terms of its abstract operations and the laws that govern them. We saw how we can still write useful functions that know nothing about their arguments except that their type forms a monoid. This more abstract mode of thinking is something we’ll develop further in the rest of part 3. We’ll consider other purely algebraic interfaces and show how they encapsulate common patterns that we’ve repeated throughout this book.