Functional Programming in Scala (2015)
Part 3. Common structures in functional design
Chapter 11. Monads
In the previous chapter, we introduced a simple algebraic structure, the monoid. This was our first instance of a completely abstract, purely algebraic interface, and it led us to think about interfaces in a new way. A useful interface may be defined only by a collection of operations related by laws.
In this chapter, we’ll continue this mode of thinking and apply it to the problem of factoring out code duplication across some of the libraries we wrote in parts 1 and 2. We’ll discover two new abstract interfaces, Functor and Monad, and get more general experience with spotting these sorts of abstract structures in our code.[1]
1 The names functor and monad come from the branch of mathematics called category theory, but it isn’t necessary to have any category theory background to follow the content in this chapter. You may be interested in following some of the references in the chapter notes for more information.
11.1. Functors: generalizing the map function
In parts 1 and 2, we implemented several different combinator libraries. In each case, we proceeded by writing a small set of primitives and then a number of combinators defined purely in terms of those primitives. We noted some similarities between derived combinators across the libraries we wrote. For instance, we implemented a map function for each data type, to lift a function taking one argument “into the context of” some data type. For Gen, Parser, and Option, the type signatures were as follows:
def map[A,B](ga: Gen[A])(f: A => B): Gen[B]
def map[A,B](pa: Parser[A])(f: A => B): Parser[B]
def map[A,B](oa: Option[A])(f: A => B): Option[A]
These type signatures differ only in the concrete data type (Gen, Parser, or Option). We can capture as a Scala trait the idea of “a data type that implements map”:
trait Functor[F[_]] {
def map[A,B](fa: F[A])(f: A => B): F[B]
}
Here we’ve parameterized map on the type constructor, F[_], much like we did with Foldable in the previous chapter.[2] Instead of picking a particular F[_], like Gen or Parser, the Functor trait is parametric in the choice of F. Here’s an instance for List:
2 Recall that a type constructor is applied to a type to produce a type. For example, List is a type constructor, not a type. There are no values of type List, but we can apply it to the type Int to produce the type List[Int]. Likewise, Parser can be applied to String to yield Parser[String].
val listFunctor = new Functor[List] {
def map[A,B](as: List[A])(f: A => B): List[B] = as map f
}
We say that a type constructor like List (or Option, or F) is a functor, and the Functor[F] instance constitutes proof that F is in fact a functor.
What can we do with this abstraction? As we did in several places throughout this book, we can discover useful functions just by playing with the operations of the interface, in a purely algebraic way. You may want to pause here to see what (if any) useful operations you can define only in terms of map.
Let’s look at one example. If we have F[(A, B)] where F is a functor, we can “distribute” the F over the pair to get (F[A], F[B]):
trait Functor[F[_]] {
...
def distribute[A,B](fab: F[(A, B)]): (F[A], F[B]) =
(map(fab)(_._1), map(fab)(_._2))
}
We wrote this just by following the types, but let’s think about what it means for concrete data types like List, Gen, Option, and so on. For example, if we distribute a List[(A, B)], we get two lists of the same length, one with all the As and the other with all the Bs. That operation is sometimes called unzip. So we just wrote a generic unzip function that works not just for lists, but for any functor!
And when we have an operation on a product like this, we should see if we can construct the opposite operation over a sum or coproduct:
def codistribute[A,B](e: Either[F[A], F[B]]): F[Either[A, B]] =
e match {
case Left(fa) => map(fa)(Left(_))
case Right(fb) => map(fb)(Right(_))
}
What does codistribute mean for Gen? If we have either a generator for A or a generator for B, we can construct a generator that produces either A or B depending on which generator we actually have.
We just came up with two really general and potentially useful combinators based purely on the abstract interface of Functor, and we can reuse them for any type that allows an implementation of map.
11.1.1. Functor laws
Whenever we create an abstraction like Functor, we should consider not only what abstract methods it should have, but which laws we expect to hold for the implementations. The laws you stipulate for an abstraction are entirely up to you,[3] and of course Scala won’t enforce any of these laws. But laws are important for two reasons:
3 Though if you’re going to borrow the name of some existing mathematical abstraction like functor or monoid, we recommend using the laws already specified by mathematics.
· Laws help an interface form a new semantic level whose algebra may be reasoned about independently of the instances. For example, when we take the product of a Monoid[A] and a Monoid[B] to form a Monoid[(A,B)], the monoid laws let us conclude that the “fused” monoid operation is also associative. We don’t need to know anything about A and B to conclude this.
· More concretely, we often rely on laws when writing various combinators derived from the functions of some abstract interface like Functor. We’ll see examples of this later.
For Functor, we’ll stipulate the familiar law we first introduced in chapter 7 for our Par data type:[4]
4 This law also comes from the mathematical definition of functor.
map(x)(a => a) == x
In other words, mapping over a structure x with the identity function should itself be an identity. This law is quite natural, and we noticed later in part 2 that this law was satisfied by the map functions of other types besides Par. This law (and its corollaries given by parametricity) capture the requirement that map(x) “preserves the structure” of x. Implementations satisfying this law are restricted from doing strange things like throwing exceptions, removing the first element of a List, converting a Some to None, and so on. Only the elements of the structure are modified by map; the shape or structure itself is left intact. Note that this law holds for List, Option, Par, Gen, and most other data types that define map!
To give a concrete example of this preservation of structure, we can consider distribute and codistribute, defined earlier. Here are their signatures again:
def distribute[A,B](fab: F[(A, B)]): (F[A], F[B])
def codistribute[A,B](e: Either[F[A], F[B]]): F[Either[A, B]]
Since we know nothing about F other than that it’s a functor, the law assures us that the returned values will have the same shape as the arguments. If the input to distribute is a list of pairs, the returned pair of lists will be of the same length as the input, and corresponding elements will appear in the same order. This kind of algebraic reasoning can potentially save us a lot of work, since we don’t have to write separate tests for these properties.
11.2. Monads: generalizing the flatMap and unit functions
Functor is just one of many abstractions that we can factor out of our libraries. But Functor isn’t too compelling, as there aren’t many useful operations that can be defined purely in terms of map. Next, we’ll look at a more interesting interface, Monad. Using this interface, we can implement a number of useful operations, once and for all, factoring out what would otherwise be duplicated code. And it comes with laws with which we can reason that our libraries work the way we expect.
Recall that for several of the data types in this book so far, we implemented map2 to “lift” a function taking two arguments. For Gen, Parser, and Option, the map2 function could be implemented as follows.
Listing 11.1. Implementing map2 for Gen, Parser, and Option
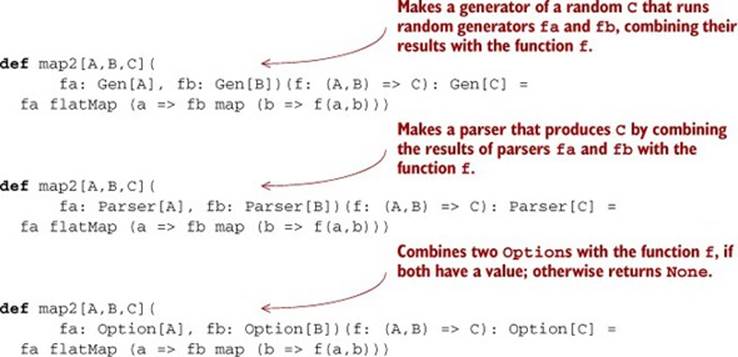
These functions have more in common than just the name. In spite of operating on data types that seemingly have nothing to do with one another, the implementations are identical! The only thing that differs is the particular data type being operated on. This confirms what we’ve suspected all along—that these are particular instances of some more general pattern. We should be able to exploit that fact to avoid repeating ourselves. For example, we should be able to write map2 once and for all in such a way that it can be reused for all of these data types.
We’ve made the code duplication particularly obvious here by choosing uniform names for our functions, taking the arguments in the same order, and so on. It may be more difficult to spot in your everyday work. But the more libraries you write, the better you’ll get at identifying patterns that you can factor out into common abstractions.
11.2.1. The Monad trait
What unites Parser, Gen, Par, Option, and many of the other data types we’ve looked at is that they’re monads. Much like we did with Functor and Foldable, we can come up with a Scala trait for Monad that defines map2 and numerous other functions once and for all, rather than having to duplicate their definitions for every concrete data type.
In part 2 of this book, we concerned ourselves with individual data types, finding a minimal set of primitive operations from which we could derive a large number of useful combinators. We’ll do the same kind of thing here to refine an abstract interface to a small set of primitives.
Let’s start by introducing a new trait, called Mon for now. Since we know we want to eventually define map2, let’s go ahead and add that.
Listing 11.2. Creating a Mon trait for map2

Here we’ve just taken the implementation of map2 and changed Parser, Gen, and Option to the polymorphic F of the Mon[F] interface in the signature.[5] But in this polymorphic context, this won’t compile! We don’t know anything about F here, so we certainly don’t know how toflatMap or map over an F[A].
5 Our decision to call the type constructor argument F here was arbitrary. We could have called this argument Foo, w00t, or Blah2, though by convention, we usually give type constructor arguments one-letter uppercase names, such as F, G, and H, or sometimes M and N, or P and Q.
What we can do is simply add map and flatMap to the Mon interface and keep them abstract. The syntax for calling these functions changes a bit (we can’t use infix syntax anymore), but the structure is otherwise the same.
Listing 11.3. Adding map and flatMap to our trait
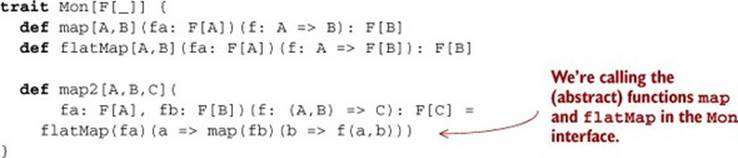
This translation was rather mechanical. We just inspected the implementation of map2, and added all the functions it called, map and flatMap, as suitably abstract methods on our interface. This trait will now compile, but before we declare victory and move on to defining instances ofMon[List], Mon[Parser], Mon[Option], and so on, let’s see if we can refine our set of primitives. Our current set of primitives is map and flatMap, from which we can derive map2. Is flatMap and map a minimal set of primitives? Well, the data types that implemented map2 all had aunit, and we know that map can be implemented in terms of flatMap and unit. For example, on Gen:
def map[A,B](f: A => B): Gen[B] =
flatMap(a => unit(f(a)))
So let’s pick unit and flatMap as our minimal set. We’ll unify under a single concept all data types that have these functions defined. The trait is called Monad, it has flat-Map and unit abstract, and it provides default implementations for map and map2.
Listing 11.4. Creating our Monad trait

The name monad
We could have called Monad anything at all, like FlatMappable, Unicorn, or Bicycle. But monad is already a perfectly good name in common use. The name comes from category theory, a branch of mathematics that has inspired a lot of functional programming concepts. The namemonad is intentionally similar to monoid, and the two concepts are related in a deep way. See the chapter notes for more information.
To tie this back to a concrete data type, we can implement the Monad instance for Gen.
Listing 11.5. Implementing Monad for Gen
object Monad {
val genMonad = new Monad[Gen] {
def unit[A](a: => A): Gen[A] = Gen.unit(a)
def flatMap[A,B](ma: Gen[A])(f: A => Gen[B]): Gen[B] =
ma flatMap f
}
}
We only need to implement unit and flatMap, and we get map and map2 at no additional cost. We’ve implemented them once and for all, for any data type for which it’s possible to supply an instance of Monad! But we’re just getting started. There are many more functions that we can implement once and for all in this manner.
Exercise 11.1
![]()
Write monad instances for Par, Parser, Option, Stream, and List.
Exercise 11.2
![]()
Hard: State looks like it would be a monad too, but it takes two type arguments and you need a type constructor of one argument to implement Monad. Try to implement a State monad, see what issues you run into, and think about possible solutions. We’ll discuss the solution later in this chapter.
11.3. Monadic combinators
Now that we have our primitives for monads, we can look back at previous chapters and see if there were some other functions that we implemented for each of our monadic data types. Many of them can be implemented once for all monads, so let’s do that now.
Exercise 11.3
![]()
The sequence and traverse combinators should be pretty familiar to you by now, and your implementations of them from various prior chapters are probably all very similar. Implement them once and for all on Monad[F].
def sequence[A](lma: List[F[A]]): F[List[A]]
def traverse[A,B](la: List[A])(f: A => F[B]): F[List[B]]
One combinator we saw for Gen and Parser was listOfN, which allowed us to replicate a parser or generator n times to get a parser or generator of lists of that length. We can implement this combinator for all monads F by adding it to our Monad trait. We should also give it a more generic name such as replicateM (meaning “replicate in a monad”).
Exercise 11.4
![]()
Implement replicateM.
def replicateM[A](n: Int, ma: F[A]): F[List[A]]
Exercise 11.5
![]()
Think about how replicateM will behave for various choices of F. For example, how does it behave in the List monad? What about Option? Describe in your own words the general meaning of replicateM.
There was also a combinator for our Gen data type, product, to take two generators and turn them into a generator of pairs, and we did the same thing for Par computations. In both cases, we implemented product in terms of map2. So we can definitely write it generically for any monadF:
def product[A,B](ma: F[A], mb: F[B]): F[(A, B)] = map2(ma, mb)((_, _))
We don’t have to restrict ourselves to combinators that we’ve seen already. It’s important to play around and see what we find.
Exercise 11.6
![]()
Hard: Here’s an example of a function we haven’t seen before. Implement the function filterM. It’s a bit like filter, except that instead of a function from A => Boolean, we have an A => F[Boolean]. (Replacing various ordinary functions like this with the monadic equivalent often yields interesting results.) Implement this function, and then think about what it means for various data types.
def filterM[A](ms: List[A])(f: A => F[Boolean]): F[List[A]]
The combinators we’ve seen here are only a small sample of the full library that Monad lets us implement once and for all. We’ll see some more examples in chapter 13.
11.4. Monad laws
In this section, we’ll introduce laws to govern our Monad interface.[6] Certainly we’d expect the functor laws to also hold for Monad, since a Monad[F]is a Functor[F], but what else do we expect? What laws should constrain flatMap and unit?
6 These laws, once again, come from the concept of monads from category theory, but a background in category theory isn’t necessary to understand this section.
11.4.1. The associative law
For example, if we wanted to combine three monadic values into one, which two should we combine first? Should it matter? To answer this question, let’s for a moment take a step down from the abstract level and look at a simple concrete example using the Gen monad.
Say we’re testing a product order system and we need to mock up some orders. We might have an Order case class and a generator for that class.
Listing 11.6. Defining our Order class

Here we’re generating the Item inline (from name and price), but there might be places where we want to generate an Item separately. So we could pull that into its own generator:
val genItem: Gen[Item] = for {
name <- Gen.stringN(3)
price <- Gen.uniform.map(_ * 10)
} yield Item(name, price)
Then we can use that in genOrder:
val genOrder: Gen[Order] = for {
item <- genItem
quantity <- Gen.choose(1,100)
} yield Order(item, quantity)
And that should do exactly the same thing, right? It seems safe to assume that. But not so fast. How can we be sure? It’s not exactly the same code.
Let’s expand both implementations of genOrder into calls to map and flatMap to better see what’s going on. In the former case, the translation is straightforward:
Gen.nextString.flatMap(name =>
Gen.nextDouble.flatMap(price =>
Gen.nextInt.map(quantity =>
Order(Item(name, price), quantity))))
But the second case looks like this (inlining the call to genItem):
Gen.nextString.flatMap(name =>
Gen.nextInt.map(price =>
Item(name, price))).flatMap(item =>
Gen.nextInt.map(quantity =>
Order(item, quantity)
Once we expand them, it’s clear that those two implementations aren’t identical. And yet when we look at the for-comprehension, it seems perfectly reasonable to assume that the two implementations do exactly the same thing. In fact, it would be surprising and weird if they didn’t. It’s because we’re assuming that flatMap obeys an associative law:
x.flatMap(f).flatMap(g) == x.flatMap(a => f(a).flatMap(g))
And this law should hold for all values x, f, and g of the appropriate types—not just for Gen but for Parser, Option, and any other monad.
11.4.2. Proving the associative law for a specific monad
Let’s prove that this law holds for Option. All we have to do is substitute None or Some(v) for x in the preceding equation and expand both sides of it.
We start with the case where x is None, and then both sides of the equal sign are
None:
None.flatMap(f).flatMap(g) == None.flatMap(a => f(a).flatMap(g))
Since None.flatMap(f) is None for all f, this simplifies to
None == None
Thus, the law holds if x is None. What about if x is Some(v) for an arbitrary choice of v? In that case, we have

Thus, the law also holds when x is Some(v) for any v. We’re now done, as we’ve shown that the law holds when x is None or when x is Some, and these are the only two possibilities for Option.
Kleisli Composition: A Clearer View on the Associative Law
It’s not so easy to see that the law we just discussed is an associative law. Remember the associative law for monoids? That was clear:
op(op(x,y), z) == op(x, op(y,z))
But our associative law for monads doesn’t look anything like that! Fortunately, there’s a way we can make the law clearer if we consider not the monadic values of types like F[A], but monadic functions of types like A => F[B]. Functions like that are called Kleisli arrows,[7] and they can be composed with one another:
7 Kleisli arrow comes from category theory and is named after the Swiss mathematician Heinrich Kleisli.
def compose[A,B,C](f: A => F[B], g: B => F[C]): A => F[C]
Exercise 11.7
![]()
Implement the Kleisli composition function compose.
We can now state the associative law for monads in a much more symmetric way:
compose(compose(f, g), h) == compose(f, compose(g, h))
Exercise 11.8
![]()
Hard: Implement flatMap in terms of compose. It seems that we’ve found another minimal set of monad combinators: compose and unit.
Exercise 11.9
![]()
Show that the two formulations of the associative law, the one in terms of flatMap and the one in terms of compose, are equivalent.
11.4.3. The identity laws
The other monad law is now pretty easy to see. Just like zero was an identity element for append in a monoid, there’s an identity element for compose in a monad. Indeed, that’s exactly what unit is, and that’s why we chose this name for this operation:[8]
8 The name unit is often used in mathematics to mean an identity for some operation.
def unit[A](a: => A): F[A]
This function has the right type to be passed as an argument to compose.[9] The effect should be that anything composed with unit is that same thing. This usually takes the form of two laws, left identity and right identity:
9 Not quite, since it takes a non-strict A to F[A] (it’s an (=> A) => F[A]), and in Scala this type is different from an ordinary A => F[A]. We’ll ignore this distinction for now, though.
compose(f, unit) == f
compose(unit, f) == f
We can also state these laws in terms of flatMap, but they’re less clear that way:
flatMap(x)(unit) == x
flatMap(unit(y))(f) == f(y)
Exercise 11.10
![]()
Prove that these two statements of the identity laws are equivalent.
Exercise 11.11
![]()
Prove that the identity laws hold for a monad of your choice.
Exercise 11.12
![]()
There’s a third minimal set of monadic combinators: map, unit, and join. Implement join in terms of flatMap.
def join[A](mma: F[F[A]]): F[A]
Exercise 11.13
![]()
Implement either flatMap or compose in terms of join and map.
Exercise 11.14
![]()
Restate the monad laws to mention only join, map, and unit.
Exercise 11.15
![]()
Write down an explanation, in your own words, of what the associative law means for Par and Parser.
Exercise 11.16
![]()
Explain in your own words what the identity laws are stating in concrete terms for Gen and List.
11.5. Just what is a monad?
Let’s now take a wider perspective. There’s something unusual about the Monad interface. The data types for which we’ve given monad instances don’t seem to have much to do with each other. Yes, Monad factors out code duplication among them, but what is a monad exactly? What does “monad” mean?
You may be used to thinking of interfaces as providing a relatively complete API for an abstract data type, merely abstracting over the specific representation. After all, a singly linked list and an array-based list may be implemented differently behind the scenes, but they’ll share a common interface in terms of which a lot of useful and concrete application code can be written. Monad, like Monoid, is a more abstract, purely algebraic interface. The Monad combinators are often just a small fragment of the full API for a given data type that happens to be a monad. So Monaddoesn’t generalize one type or another; rather, many vastly different data types can satisfy the Monad interface and laws.
We’ve seen three minimal sets of primitive Monad combinators, and instances of Monad will have to provide implementations of one of these sets:
· unit and flatMap
· unit and compose
· unit, map, and join
And we know that there are two monad laws to be satisfied, associativity and identity, that can be formulated in various ways. So we can state plainly what a monad is:
A monad is an implementation of one of the minimal sets of monadic combinators, satisfying the laws of associativity and identity.
That’s a perfectly respectable, precise, and terse definition. And if we’re being precise, this is the only correct definition. A monad is precisely defined by its operations and laws; no more, no less. But it’s a little unsatisfying. It doesn’t say much about what it implies—what a monad means. The problem is that it’s a self-contained definition. Even if you’re a beginning programmer, you have by now obtained a vast amount of knowledge related to programming, and this definition integrates with none of that.
In order to really understand what’s going on with monads, try to think about monads in terms of things you already know and connect them to a wider context. To develop some intuition for what monads mean, let’s look at another couple of monads and compare their behavior.
11.5.1. The identity monad
To distill monads to their essentials, let’s look at the simplest interesting specimen, the identity monad, given by the following type:
case class Id[A](value: A)
Exercise 11.17
![]()
Implement map and flatMap as methods on this class, and give an implementation for Monad[Id].
Now, Id is just a simple wrapper. It doesn’t really add anything. Applying Id to A is an identity since the wrapped type and the unwrapped type are totally isomorphic (we can go from one to the other and back again without any loss of information). But what is the meaning of the identitymonad? Let’s try using it in the REPL:
scala> Id("Hello, ") flatMap (a =>
| Id("monad!") flatMap (b =>
| Id(a + b)))
res0: Id[java.lang.String] = Id(Hello, monad!)
When we write the exact same thing with a for-comprehension, it might be clearer:
scala> for {
| a <- Id("Hello, ")
| b <- Id("monad!")
| } yield a + b
res1: Id[java.lang.String] = Id(Hello, monad!)
So what is the action of flatMap for the identity monad? It’s simply variable substitution. The variables a and b get bound to "Hello, " and "monad!", respectively, and then substituted into the expression a + b. We could have written the same thing without the Id wrapper, using just Scala’s own variables:
scala> val a = "Hello, "
a: java.lang.String = "Hello, "
scala> val b = "monad!"
b: java.lang.String = monad!
scala> a + b
res2: java.lang.String = Hello, monad!
Besides the Id wrapper, there’s no difference. So now we have at least a partial answer to the question of what monads mean. We could say that monads provide a context for introducing and binding variables, and performing variable substitution.
Let’s see if we can get the rest of the answer.
11.5.2. The State monad and partial type application
Look back at the discussion of the State data type in chapter 6. Recall that we implemented some combinators for State, including map and flatMap.
Listing 11.7. Revisiting our State data type
case class State[S, A](run: S => (A, S)) {
def map[B](f: A => B): State[S, B] =
State(s => {
val (a, s1) = run(s)
(f(a), s1)
})
def flatMap[B](f: A => State[S, B]): State[S, B] =
State(s => {
val (a, s1) = run(s)
f(a).run(s1)
})
}
It looks like State definitely fits the profile for being a monad. But its type constructor takes two type arguments, and Monad requires a type constructor of one argument, so we can’t just say Monad[State]. But if we choose some particular S, then we have something like State[S, _], which is the kind of thing expected by Monad. So State doesn’t just have one monad instance but a whole family of them, one for each choice of S. We’d like to be able to partially apply State to where the S type argument is fixed to be some concrete type.
This is much like how we might partially apply a function, except at the type level. For example, we can create an IntState type constructor, which is an alias for State with its first type argument fixed to be Int:
type IntState[A] = State[Int, A]
And IntState is exactly the kind of thing that we can build a Monad for:
object IntStateMonad extends Monad[IntState] {
def unit[A](a: => A): IntState[A] = State(s => (a, s))
def flatMap[A,B](st: IntState[A])(f: A => IntState[B]): IntState[B] =
st flatMap f
}
Of course, it would be really repetitive if we had to manually write a separate Monad instance for each specific state type. Unfortunately, Scala doesn’t allow us to use underscore syntax to simply say State[Int, _] to create an anonymous type constructor like we create anonymous functions. But instead we can use something similar to lambda syntax at the type level. For example, we could have declared IntState directly inline like this:
object IntStateMonad extends
Monad[({type IntState[A] = State[Int, A]})#IntState] {
...
}
This syntax can be jarring when you first see it. But all we’re doing is declaring an anonymous type within parentheses. This anonymous type has, as one of its members, the type alias IntState, which looks just like before. Outside the parentheses we’re then accessing its IntStatemember with the # syntax. Just like we can use a dot (.) to access a member of an object at the value level, we can use the # symbol to access a type member (see the “Type Projection” section of the Scala Language Specification: http://mng.bz/u70U).
A type constructor declared inline like this is often called a type lambda in Scala. We can use this trick to partially apply the State type constructor and declare a State-Monad trait. An instance of StateMonad[S] is then a monad instance for the given state type S:

Again, just by giving implementations of unit and flatMap, we get implementations of all the other monadic combinators for free.
Exercise 11.18
![]()
Now that we have a State monad, you should try it out to see how it behaves. What is the meaning of replicateM in the State monad? How does map2 behave? What about sequence?
Let’s now look at the difference between the Id monad and the State monad. Remember that the primitive operations on State (besides the monadic operations unit and flatMap) are that we can read the current state with getState and we can set a new state with setState:
def getState[S]: State[S, S]
def setState[S](s: => S): State[S, Unit]
Remember that we also discovered that these combinators constitute a minimal set of primitive operations for State. So together with the monadic primitives (unit and flatMap) they completely specify everything that we can do with the State data type. This is true in general for monads—they all have unit and flatMap, and each monad brings its own set of additional primitive operations that are specific to it.
Exercise 11.19
![]()
What laws do you expect to mutually hold for getState, setState, unit, and flatMap?
What does this tell us about the meaning of the State monad? Let’s study a simple example. The details of this code aren’t too important, but notice the use of getState and setState in the for block.
Listing 11.8. Getting and setting state with a for-comprehension
val F = stateMonad[Int]
def zipWithIndex[A](as: List[A]): List[(Int,A)] =
as.foldLeft(F.unit(List[(Int, A)]()))((acc,a) => for {
xs <- acc
n <- getState
_ <- setState(n + 1)
} yield (n, a) :: xs).run(0)._1.reverse
This function numbers all the elements in a list using a State action. It keeps a state that’s an Int, which is incremented at each step. We run the whole composite state action starting from 0. We then reverse the result since we constructed it in reverse order.[10]
10 This is asymptotically faster than appending to the list in the loop.
Note what’s going on with getState and setState in the for-comprehension. We’re obviously getting variable binding just like in the Id monad—we’re binding the value of each successive state action (getState, acc, and then setState) to variables. But there’s more going on, literally between the lines. At each line in the for-comprehension, the implementation of flatMap is making sure that the current state is available to getState, and that the new state gets propagated to all actions that follow a setState.
What does the difference between the action of Id and the action of State tell us about monads in general? We can see that a chain of flatMap calls (or an equivalent for-comprehension) is like an imperative program with statements that assign to variables, and the monad specifies what occurs at statement boundaries. For example, with Id, nothing at all occurs except unwrapping and rewrapping in the Id constructor. With State, the most current state gets passed from one statement to the next. With the Option monad, a statement may return None and terminate the program. With the List monad, a statement may return many results, which causes statements that follow it to potentially run multiple times, once for each result.
The Monad contract doesn’t specify what is happening between the lines, only that whatever is happening satisfies the laws of associativity and identity.
Exercise 11.20
![]()
Hard: To cement your understanding of monads, give a monad instance for the following type, and explain what it means. What are its primitive operations? What is the action of flatMap? What meaning does it give to monadic functions like sequence, join, and replicateM? What meaning does it give to the monad laws?[11]
11 See the chapter notes for further discussion of this data type.
case class Reader[R, A](run: R => A)
object Reader {
def readerMonad[R] = new Monad[({type f[x] = Reader[R,x]})#f] {
def unit[A](a: => A): Reader[R,A]
def flatMap[A,B](st: Reader[R,A])(f: A => Reader[R,B]): Reader[R,B]
}
}
11.6. Summary
In this chapter, we took a pattern that we’ve seen repeated throughout the book and we unified it under a single concept: monad. This allowed us to write a number of combinators once and for all, for many different data types that at first glance don’t seem to have anything in common. We discussed laws that they all satisfy, the monad laws, from various perspectives, and we developed some insight into what it all means.
An abstract topic like this can’t be fully understood all at once. It requires an iterative approach where you keep revisiting the topic from different perspectives. When you discover new monads or new applications of them, or see them appear in a new context, you’ll inevitably gain new insight. And each time it happens, you might think to yourself, “OK, I thought I understood monads before, but now I really get it.”