Functional Programming in Scala (2015)
Part 4. Effects and I/O
Functional programming is a complete programming paradigm. All programs that we can imagine can be expressed functionally, including those that mutate data in place and interact with the external world by writing to files or reading from databases. In this part, we’ll apply what we covered in parts 1–3 of this book to show how FP can express these effectful programs.
We’ll begin in the next chapter by examining the most straightforward handling of external effects, using an I/O monad. This is a simplistic embedding of an imperative programming language into a functional language. The same general approach can be used for handling local effects and mutation, which we’ll introduce in chapter 14. Both of these chapters will motivate the development of more composable ways to deal with effects. In chapter 15, our final chapter, we’ll develop a library for streaming I/O, and discuss how to write compositional and modular programs that incrementally process I/O streams.
Our goal in this part of the book is not to cover absolutely every technique relevant to handling I/O and mutation, but to introduce the essential ideas and equip you with a conceptual framework for future learning. You’ll undoubtedly encounter problems that don’t look exactly like those discussed here. But along with parts 1–3, after finishing this part you’ll be in good position to apply FP to whatever programming tasks you may face.
Chapter 13. External effects and I/O
In this chapter, we’ll take what we’ve learned so far about monads and algebraic data types and extend it to handle external effects like reading from databases and writing to files. We’ll develop a monad for I/O, aptly called IO, that will allow us to handle such external effects in a purely functional way.
We’ll make an important distinction in this chapter between effects and side effects. The IO monad provides a straightforward way of embedding imperative programming with I/O effects in a pure program while preserving referential transparency. It clearly separates effectful code—code that needs to have some effect on the outside world—from the rest of our program.
This will also illustrate a key technique for dealing with external effects—using pure functions to compute a description of an effectful computation, which is then executed by a separate interpreter that actually performs those effects. Essentially we’re crafting an embedded domain-specific language (EDSL) for imperative programming. This is a powerful technique that we’ll use throughout the rest of part 4. Our goal is to equip you with the skills needed to craft your own EDSLs for describing effectful programs.
13.1. Factoring effects
We’ll work our way up to the IO monad by first considering a simple example of a program with side effects.
Listing 13.1. Program with side effects
case class Player(name: String, score: Int)
def contest(p1: Player, p2: Player): Unit =
if (p1.score > p2.score)
println(s"${p1.name} is the winner!")
else if (p2.score > p1.score)
println(s"${p2.name} is the winner!")
else
println("It's a draw.")
The contest function couples the I/O code for displaying the result to the pure logic for computing the winner. We can factor the logic into its own pure function, winner:

It is always possible to factor an impure procedure into a pure “core” function and two procedures with side effects: one that supplies the pure function’s input and one that does something with the pure function’s output. In listing 13.1, we factored the pure function winner out of contest. Conceptually, contest had two responsibilities—it was computing the result of the contest, and it was displaying the result that was computed. With the refactored code, winner has a single responsibility: to compute the winner. The contest method retains the responsibility of printing the result of winner to the console.
We can refactor this even further. The contest function still has two responsibilities: it’s computing which message to display and then printing that message to the console. We could factor out a pure function here as well, which might be beneficial if we later decide to display the result in some sort of UI or write it to a file instead. Let’s perform this refactoring now:

Note how the side effect, println, is now only in the outermost layer of the program, and what’s inside the call to println is a pure expression.
This might seem like a simplistic example, but the same principle applies in larger, more complex programs, and we hope you can see how this sort of refactoring is quite natural. We aren’t changing what our program does, just the internal details of how it’s factored into smaller functions. The insight here is that inside every function with side effects is a pure function waiting to get out.
We can formalize this insight a bit. Given an impure function f of type A => B, we can split f into two functions:
· A pure function of type A => D, where D is some description of the result of f.
· An impure function of type D => B, which can be thought of as an interpreter of these descriptions.
We’ll extend this to handle “input” effects shortly. For now, let’s consider applying this strategy repeatedly to a program. Each time we apply it, we make more functions pure and push side effects to the outer layers. We could call these impure functions the “imperative shell” around the pure “core” of the program. Eventually, we reach functions that seem to necessitate side effects like the built-in println, which has type String => Unit. What do we do then?
13.2. A simple IO type
It turns out that even procedures like println are doing more than one thing. And they can be factored in much the same way, by introducing a new data type that we’ll call IO:
trait IO { def run: Unit }
def PrintLine(msg: String): IO =
new IO { def run = println(msg) }
def contest(p1: Player, p2: Player): IO =
PrintLine(winnerMsg(winner(p1, p2)))
Our contest function is now pure—it returns an IO value, which simply describes an action that needs to take place, but doesn’t actually execute it. We say that contest has (or produces) an effect or is effectful, but it’s only the interpreter of IO (its run method) that actually has a sideeffect. Now contest only has one responsibility, which is to compose the parts of the program together: winner to compute who the winner is, winnerMsg to compute what the resulting message should be, and Print-Line to indicate that the message should be printed to the console. But the responsibility of interpreting the effect and actually manipulating the console is held by the run method on IO.
Other than technically satisfying the requirements of referential transparency, has the IO type actually bought us anything? That’s a personal value judgement. As with any other data type, we can assess the merits of IO by considering what sort of algebra it provides—is it something interesting, from which we can define a large number of useful operations and programs, with nice laws that give us the ability to reason about what these larger programs will do? Not really. Let’s look at the operations we can define:

The only thing we can perhaps say about IO as it stands right now is that it forms a Monoid (empty is the identity, and ++ is the associative operation). So if we have, for example, a List[IO], we can reduce that to a single IO, and the associativity of ++ means that we can do this either by folding left or folding right. On its own, this isn’t very interesting. All it seems to have given us is the ability to delay when a side effect actually happens.
Now we’ll let you in on a secret: you, as the programmer, get to invent whatever API you wish to represent your computations, including those that interact with the universe external to your program. This process of crafting pleasing, useful, and composable descriptions of what you want your programs to do is at its core language design. You’re crafting a little language, and an associated interpreter, that will allow you to express various programs. If you don’t like something about this language you’ve created, change it! You should approach this like any other design task.
13.2.1. Handling input effects
As you’ve seen before, sometimes when building up a little language you’ll encounter a program that it can’t express. So far our IO type can represent only “output” effects. There’s no way to express IO computations that must, at various points, wait for input from some external source. Suppose we wanted to write a program that prompts the user for a temperature in degrees Fahrenheit, and then converts this value to Celsius and echoes it to the user. A typical imperative program might look something like this.[1]
1 We’re not doing any sort of error handling here. This is just meant to be an illustrative example.
Listing 13.2. Imperative program that converts Fahrenheit to Celsius
def fahrenheitToCelsius(f: Double): Double =
(f - 32) * 5.0/9.0
def converter: Unit = {
println("Enter a temperature in degrees Fahrenheit: ")
val d = readLine.toDouble
println(fahrenheitToCelsius(d))
}
Unfortunately, we run into problems if we want to make converter into a pure function that returns an IO:
def fahrenheitToCelsius(f: Double): Double =
(f - 32) * 5.0/9.0
def converter: IO = {
val prompt: IO = PrintLine(
"Enter a temperature in degrees Fahrenheit: ")
// now what ???
}
In Scala, readLine is a def with the side effect of capturing a line of input from the console. It returns a String. We could wrap a call to readLine in IO, but we have nowhere to put the result! We don’t yet have a way of representing this sort of effect. The problem is that our current IOtype can’t express computations that yield a value of some meaningful type—our interpreter of IO just produces Unit as its output. Should we give up on our IO type and resort to using side effects? Of course not! We extend our IO type to allow input, by adding a type parameter:
sealed trait IO[A] { self =>
def run: A
def map[B](f: A => B): IO[B] =
new IO[B] { def run = f(self.run) }
def flatMap[B](f: A => IO[B]): IO[B] =
new IO[B] { def run = f(self.run).run }
}
An IO computation can now return a meaningful value. Note that we’ve added map and flatMap functions so IO can be used in for-comprehensions. And IO now forms a Monad:

We can now write our converter example:
def ReadLine: IO[String] = IO { readLine }
def PrintLine(msg: String): IO[Unit] = IO { println(msg) }
def converter: IO[Unit] = for {
_ <- PrintLine("Enter a temperature in degrees Fahrenheit: ")
d <- ReadLine.map(_.toDouble)
_ <- PrintLine(fahrenheitToCelsius(d).toString)
} yield ()
Our converter definition no longer has side effects—it’s a referentially transparent description of a computation with effects, and converter.run is the interpreter that will actually execute those effects. And because IO forms a Monad, we can use all the monadic combinators we wrote previously. Here are some other example usages of IO:
· val echo = ReadLine.flatMap(PrintLine)—An IO[Unit] that reads a line from the console and echoes it back
· val readInt = ReadLine.map(_.toInt)—An IO[Int] that parses an Int by reading a line from the console
· val readInts = readInt ** readInt—An IO[(Int,Int)] that parses an (Int,Int) by reading two lines from the console[2]
2 Recall that a ** b is the same as map2(a,b)((_,_)); it combines two effects into a pair of their results.
· replicateM(10)(ReadLine) —An IO[List[String]] that will read 10 lines from the console and return the list of results[3]
3 Recall that replicateM(3)(fa) is the same as sequence(List(fa,fa,fa)).
Let’s do a larger example—an interactive program that prompts the user for input in a loop and then computes the factorial of the input. Here’s an example run:
The Amazing Factorial REPL, v2.0
q - quit
<number> - compute the factorial of the given number
<anything else> - crash spectacularly
3
factorial: 6
7
factorial: 5040
q
The code for this is shown in listing 13.3. It uses a few Monad functions we haven’t seen yet: when, foreachM, and sequence_, discussed in the sidebar. For the full listing, see the associated chapter code. The details of this code aren’t too important; the point here is just to demonstrate how we can embed an imperative programming language into the purely functional subset of Scala. All the usual imperative programming tools are here—we can write loops, perform I/O, and so on.
Listing 13.3. An imperative program with a doWhile loop

Additional monad combinators
Listing 13.3 makes use of some monad combinators we haven’t seen before, although they can be defined for any Monad. You may want to think about what these combinators mean for types other than IO. Note that not all of them make sense for every monadic type. (For instance, what doesforever mean for Option? For Stream?)

We don’t necessarily endorse writing code this way in Scala.[4] But it does demonstrate that FP is not in any way limited in its expressiveness—every program can be expressed in a purely functional way, even if that functional program is a straightforward embedding of an imperative program into the IO monad.
4 If you have a monolithic block of impure code like this, you can always just write a definition that performs actual side effects and then wrap it in IO—this will be more efficient, and the syntax is nicer than what’s provided using a combination of for-comprehension syntax and the various Monad combinators.
13.2.2. Benefits and drawbacks of the simple IO type
An IO monad like what we have so far is a kind of least common denominator for expressing programs with external effects. Its usage is important mainly because it clearly separates pure code from impure code, forcing us to be honest about where interactions with the outside world are occurring. It also encourages the beneficial factoring of effects that we discussed earlier. But when programming within the IO monad, we have many of the same difficulties as we would in ordinary imperative programming, which has motivated functional programmers to look for more composable ways of describing effectful programs.[5] Nonetheless, our IO monad does provide some real benefits:
5 We’ll see an example of this in chapter 15 when we develop a data type for composable streaming I/O.
· IO computations are ordinary values. We can store them in lists, pass them to functions, create them dynamically, and so on. Any common pattern can be wrapped up in a function and reused.
· Reifying IO computations as values means we can craft a more interesting interpreter than the simple run method baked into the IO type itself. Later in this chapter, we’ll build a more refined IO type and sketch out an interpreter that uses non-blocking I/O in its implementation. What’s more, as we vary the interpreter, client code like the converter example remains identical—we don’t expose the representation of IO to the programmer at all! It’s entirely an implementation detail of our IO interpreter.
Our naive IO monad also has a few problems:
· Many IO programs will overflow the runtime call stack and throw a Stack-OverflowError. If you haven’t encountered this problem yet in your own experimenting, you’d certainly run into it if you were to write larger programs using our current IO type. For example, if you keep typing numbers into the factorialREPL program from earlier, it eventually overflows the stack.
· A value of type IO[A] is completely opaque. It’s really just a lazy identity—a function that takes no arguments. When we call run, we hope that it will eventually produce a value of type A, but there’s no way for us to inspect such a program and see what it might do. It might hang forever and do nothing, or it might eventually do something productive. There’s no way to tell. We could say that it’s too general, and as a result there’s little reasoning that we can do with IO values. We can compose them with the monadic combinators, or we can run them, but that’s all we can do.
· Our simple IO type has nothing at all to say about concurrency or asynchronous operations. The primitives we have so far only allow us to sequence opaque blocking IO actions one after another. Many I/O libraries, such as the java.nio package that comes with the standard libraries, allow non-blocking and asynchronous I/O. Our IO type is incapable of making use of such operations. We’ll rectify that by the end of this chapter when we develop a more practical IO monad.
Let’s start by solving the first problem (overflowing the call stack), since it will inform our solution for the other two.
13.3. Avoiding the StackOverflowError
To better understand the StackOverflowError, consider this very simple program that demonstrates the problem:
val p = IO.forever(PrintLine("Still going..."))
If we evaluate p.run, it will crash with a StackOverflowError after printing a few thousand lines. If you look at the stack trace, you’ll see that run is calling itself over and over. The problem is in the definition of flatMap:
def flatMap[B](f: A => IO[B]): IO[B] =
new IO[B] { def run = f(self.run).run }
This method creates a new IO object whose run definition calls run again before calling f. This will keep building up nested run calls on the stack and eventually overflow it. What can be done about this?
13.3.1. Reifying control flow as data constructors
The answer is surprisingly simple. Instead of letting program control just flow through with function calls, we explicitly bake into our data type the control flow that we want to support. For example, instead of making flatMap a method that constructs a new IO in terms of run, we can just make it a data constructor of the IO data type. Then the interpreter can be a tail-recursive loop. Whenever it encounters a constructor like FlatMap(x,k), it will simply interpret x and then call k on the result. Here’s a new IO type that implements that idea.
Listing 13.4. Creating a new IO type

This new IO type has three data constructors, representing the three different kinds of control flow that we want the interpreter of this data type to support. Return represents an IO action that has finished, meaning that we want to return the value a without any further steps. Suspend means that we want to execute some effect to produce a result. And the FlatMap data constructor lets us extend or continue an existing computation by using the result of the first computation to produce a second computation. The flatMap method’s implementation can now simply call theFlatMap data constructor and return immediately. When the interpreter encounters FlatMap(sub, k), it can interpret the subcomputation sub and then remember to call the continuation k on the result. Then k will continue executing the program.
We’ll get to the interpreter shortly, but first let’s rewrite our printLine example to use this new IO type:
def printLine(s: String): IO[Unit] =
Suspend(() => Return(println(s)))
val p = IO.forever(printLine("Still going..."))
What this actually creates is an infinite nested structure, much like a Stream. The “head” of the stream is a Function0, and the rest of the computation is like the “tail”:
FlatMap(Suspend(() => println(s)),
_ => FlatMap(Suspend(() => println(s)),
_ => FlatMap(...)))
And here’s the tail-recursive interpreter that traverses the structure and performs the effects:

Note that instead of saying run(f(run(x))) in the FlatMap(x,f) case (thereby losing tail recursion), we instead pattern match on x, since it can only be one of three things. If it’s a Return, we can just call f on the pure value inside. If it’s a Suspend, then we can just execute its resumption, call FlatMap with f on its result, and recurse. But if x is itself a FlatMap constructor, then we know that io consists of two FlatMap constructors nested on the left like this: FlatMap(FlatMap(y,g),f).
In order to continue running the program in that case, the next thing we naturally want to do is look at y to see if it is another FlatMap constructor, but the expression may be arbitrarily deep and we want to remain tail-recursive. We reassociate this to the right, effectively turning (y flatMap g) flatMap f into y flatMap (a => g(a) flatMap f). We’re just taking advantage of the monad associativity law! Then we call run on the rewritten expression, letting us remain tail-recursive. Thus, when we actually interpret our program, it will be incrementally rewritten to be a right-associated sequence of FlatMap constructors:
FlatMap(a1, a1 =>
FlatMap(a2, a2 =>
FlatMap(a3, a3 =>
...
FlatMap(aN, aN => Return(aN)))))
If we now pass our example program p to run, it’ll continue running indefinitely without a stack overflow, which is what we want. Our run function won’t overflow the stack, even for infinitely recursive IO programs.
What have we done here? When a program running on the JVM makes a function call, it’ll push a frame onto the call stack in order to remember where to return after the call has finished so that the execution can continue. We’ve made this program control explicit in our IO data type. Whenrun interprets an IO program, it’ll determine whether the program is requesting to execute some effect with a Suspend(s), or whether it wants to call a subroutine with FlatMap(x,f). Instead of the program making use of the call stack, run will call x() and then continue by calling f on the result of that. And f will immediately return either a Suspend, a FlatMap, or a Return, transferring control to run again. Our IO program is therefore a kind of coroutine [6] that executes cooperatively with run. It continually makes either Suspend or FlatMap requests, and every time it does so, it suspends its own execution and returns control to run. And it’s actually run that drives the execution of the program forward, one such suspension at a time. A function like run is sometimes called a trampoline, and the overall technique of returning control to a single loop to eliminate the stack is called trampolining.
6 If you aren’t familiar with the term coroutine, you may want to check out the Wikipedia page (http://mng.bz/ALiI), but it’s not essential to following the rest of this chapter.
13.3.2. Trampolining: a general solution to stack overflow
Nothing says that the resume functions in our IO monad have to perform side effects. The IO type we have so far is in fact a general data structure for trampolining computations—even pure computations that don’t do any I/O at all!
The StackOverflowError problem manifests itself in Scala wherever we have a composite function that consists of more function calls than there’s space for on the call stack. This problem is easy to demonstrate:

And it’ll likely fail for much smaller compositions. Fortunately, we can solve this with our IO monad:

But there’s no I/O going on here at all. So IO is a bit of a misnomer. It really gets that name from the fact that Suspend can contain a side-effecting function. But what we have is not really a monad for I/O—it’s actually a monad for tail-call elimination! Let’s change its name to reflect that:
sealed trait TailRec[A] {
def flatMap[B](f: A => TailRec[B]): TailRec[B] =
FlatMap(this, f)
def map[B](f: A => B): TailRec[B] =
flatMap(f andThen (Return(_)))
}
case class Return[A](a: A) extends TailRec[A]
case class Suspend[A](resume: () => A) extends TailRec[A]
case class FlatMap[A,B](sub: TailRec[A],
k: A => TailRec[B]) extends TailRec[B]
We can use the TailRec data type to add trampolining to any function type A => B by modifying the return type B to TailRec[B] instead. We just saw an example where we changed a program that used Int => Int to use Int => TailRec[Int]. The program just had to be modified to use flatMap in function composition[7] and to Suspend before every function call.
7 This is just Kleisli composition from chapter 11. In other words, the trampolined function uses Kleisli composition in the TailRec monad instead of ordinary function composition.
Using TailRec can be slower than direct function calls, but its advantage is that we gain predictable stack usage.[8]
8 When we use TailRec to implement tail calls that wouldn’t be otherwise optimized, it’s faster than using direct calls (not to mention stack-safe). It seems that the overhead of building and tearing down stack frames is greater than the overhead of having all calls be wrapped in a Suspend. There are variations on TailRec that we haven’t investigated in detail—it isn’t necessary to transfer control to the central loop after every function call, only periodically to avoid stack overflows. We can, for example, implement the same basic idea using exceptions. See Throw.scala in the chapter code.
13.4. A more nuanced IO type
If we use TrailRec as our IO type, this solves the stack overflow problem, but the other two problems with the monad still remain—it’s inexplicit about what kinds of effects may occur, and it has no concurrency mechanism or means of performing I/O without blocking the current thread of execution.
During execution, the run interpreter will look at a TailRec program such as FlatMap(Suspend(s),k), in which case the next thing to do is to call s(). The program is returning control to run, requesting that it execute some effect s, wait for the result, and respond by passing the resulting value to k (which may subsequently return a further request). At the moment, the interpreter can’t know anything about what kind of effects the program is going to have. It’s completely opaque. So the only thing it can do is call s(). Not only can that have an arbitrary and unknowable side effect, there’s no way that the interpreter could allow asynchronous calls if it wanted to. Since the suspension is a Function0, all we can do is call it and wait for it to complete.
What if we used Par from chapter 7 for the suspension instead of Function0? Let’s call this type Async, since the interpreter can now support asynchronous execution.
Listing 13.5. Defining our Async type
sealed trait Async[A] {
def flatMap[B](f: A => Async[B]): Async[B] =
FlatMap(this, f)
def map[B](f: A => B): Async[B] =
flatMap(f andThen (Return(_)))
}
case class Return[A](a: A) extends Async[A]
case class Suspend[A](resume: Par[A]) extends Async[A]
case class FlatMap[A,B](sub: Async[A],
k: A => Async[B]) extends Async[B]
Note that the resume argument to Suspend is now a Par[A] rather than a () => A (or a Function0[A]). The implementation of run changes accordingly—it now returns a Par[A] rather than an A, and we rely on a separate tail-recursive step function to reassociate the FlatMapconstructors:
@annotation.tailrec
def step[A](async: Async[A]): Async[A] = async match {
case FlatMap(FlatMap(x,f), g) => step(x flatMap (a => f(a) flatMap g))
case FlatMap(Return(x), f) => step(f(x))
case _ => async
}
def run[A](async: Async[A]): Par[A] = step(async) match {
case Return(a) => Par.unit(a)
case Suspend(r) => Par.flatMap(r)(a => run(a))
case FlatMap(x, f) => x match {
case Suspend(r) => Par.flatMap(r)(a => run(f(a)))
case _ => sys.error("Impossible; `step` eliminates these cases")
}
}
Our Async data type now supports asynchronous computations—we can embed them using the Suspend constructor, which takes an arbitrary Par. This works, but we take this idea one step further and abstract over the choice of type constructor used in Suspend. To do that, we’ll generalize TailRec / Async and parameterize it on some type constructor F rather than use Function0 or Par specifically. We’ll name this more abstract data type Free:

Then TailRec and Async are simply type aliases:
type TailRec[A] = Free[Function0,A]
type Async[A] = Free[Par,A]
13.4.1. Reasonably priced monads
The Return and FlatMap constructors witness that this data type is a monad for any choice of F, and since they’re exactly the operations required to generate a monad, we say that it’s a free monad.[9]
9 “Free” in this context means generated freely in the sense that F itself doesn’t need to have any monadic structure of its own. See the chapter notes for a more formal statement of what “free” means.
Exercise 13.1
![]()
Free is a monad for any choice of F. Implement map and flatMap methods on the Free trait, and give the Monad instance for Free[F,_].[10]
10 Note that we must use the “type lambda” trick discussed in chapter 10 to partially apply the Free type constructor.
def freeMonad[F[_]]: Monad[({type f[a] = Free[F,a]})#f]
Exercise 13.2
![]()
Implement a specialized tail-recursive interpreter, runTrampoline, for running a Free[Function0,A].
@annotation.tailrec
def runTrampoline[A](a: Free[Function0,A]): A
Exercise 13.3
![]()
Hard: Implement a generic interpreter for Free[F,A], given a Monad[F]. You can pattern your implementation after the Async interpreter given previously, including use of a tail-recursive step function.
def run[F[_],A](a: Free[F,A])(implicit F: Monad[F]): F[A]
What is the meaning of Free[F,A]? Essentially, it’s a recursive structure that contains a value of type A wrapped in zero or more layers of F.[11] It’s a monad because flatMap lets us take the A and from it generate more layers of F. Before getting at the result, an interpreter of the structure must be able to process all of those F layers. We can view the structure and its interpreter as coroutines that are interacting, and the type F defines the protocol of this interaction. By choosing our F carefully, we can precisely control what kinds of interactions are allowed.
11 Put another way, it’s a tree with data of type A at the leaves, where the branching is described by F. Put yet another way, it’s an abstract syntax tree for a program in a language whose instructions are given by F, with free variables in A.
13.4.2. A monad that supports only console I/O
Function0 is not just the simplest possible choice for the type parameter F, but also one of the least restrictive in terms of what’s allowed. This lack of restriction gives us no ability to reason about what a value of type Function0[A] might do. A more restrictive choice for F inFree[F,A] might be an algebraic data type that only models interaction with the console.
Listing 13.6. Creating our Console type

A Console[A] represents a computation that yields an A, but it’s restricted to one of two possible forms: ReadLine (having type Console[Option[String]]) or PrintLine. We bake two interpreters into Console, one that converts to a Par, and another that converts to a Function0. The implementations of these interpreters are straightforward.
We can now embed this data type into Free to obtain a restricted IO type allowing for only console I/O. We just use the Suspend constructor of Free:
object Console {
type ConsoleIO[A] = Free[Console, A]
def readLn: ConsoleIO[Option[String]] =
Suspend(ReadLine)
def printLn(line: String): ConsoleIO[Unit] =
Suspend(PrintLine(line))
}
Using the Free[Console,A] type, or equivalently ConsoleIO[A], we can write programs that interact with the console, and we reasonably expect that they don’t perform other kinds of I/O:[12]
12 Of course, a Scala program could always technically have side effects but we’re assuming that the programmer has adopted the discipline of programming without side effects, since Scala can’t guarantee this for us.

This sounds good, but how do we actually run a ConsoleIO? Recall our signature for run:
def run[F[_],A](a: Free[F,A])(implicit F: Monad[F]): F[A]
In order to run a Free[Console,A], we seem to need a Monad[Console], which we don’t have. Note that it’s not possible to implement flatMap for Console:
sealed trait Console[A] {
def flatMap[B](f: A => Console[B]): Console[B] = this match {
case ReadLine => ???
case PrintLine(s) => ???
}
}
We must translate our Console type, which doesn’t form a monad, to some other type (like Function0 or Par) that does. We’ll make use of the following type to do this translation:

val consoleToFunction0 =
new (Console ~> Function0) { def apply[A](a: Console[A]) = a.toThunk }
val consoleToPar =
new (Console ~> Par) { def apply[A](a: Console[A]) = a.toPar }
Using this type, we can generalize our earlier implementation of run slightly:
def runFree[F[_],G[_],A](free: Free[F,A])(t: F ~> G)(
implicit G: Monad[G]): G[A] =
step(free) match {
case Return(a) => G.unit(a)
case Suspend(r) => t(r)
case FlatMap(Suspend(r),f) => G.flatMap(t(r))(a => runFree(f(a))(t))
case _ => sys.error("Impossible; `step` eliminates these cases")
We accept a value of type F ~> G and perform the translation as we interpret the Free[F,A] program. Now we can implement the convenience functions runConsoleFunction0 and runConsolePar to convert a Free[Console,A] to either Function0[A] or Par[A]:
def runConsoleFunction0[A](a: Free[Console,A]): () => A =
runFree[Console,Function0,A](a)(consoleToFunction0)
def runConsolePar[A](a: Free[Console,A]): Par[A] =
runFree[Console,Par,A](a)(consoleToPar)
This relies on having Monad[Function0] and Monad[Par] instances:
implicit val function0Monad = new Monad[Function0] {
def unit[A](a: => A) = () => a
def flatMap[A,B](a: Function0[A])(f: A => Function0[B]) =
() => f(a())()
}
implicit val parMonad = new Monad[Par] {
def unit[A](a: => A) = Par.unit(a)
def flatMap[A,B](a: Par[A])(f: A => Par[B]) =
Par.fork { Par.flatMap(a)(f) }
}
Exercise 13.4
![]()
Hard: It turns out that runConsoleFunction0 isn’t stack-safe, since flatMap isn’t stack-safe for Function0 (it has the same problem as our original, naive IO type in which run called itself in the implementation of flatMap). Implement translate using runFree, and then use it to implement runConsole in a stack-safe way.
def translate[F[_],G[_],A](f: Free[F,A])(fg: F ~> G): Free[G,A]
def runConsole[A](a: Free[Console,A]): A
A value of type Free[F,A] is like a program written in an instruction set provided by F. In the case of Console, the two instructions are PrintLine and ReadLine. The recursive scaffolding (Suspend) and monadic variable substitution (FlatMap and Return) are provided by Freeitself. We can introduce other choices of F for different instruction sets, for example, different I/O capabilities—a file system F granting read/write access (or even just read access) to the file system. Or we could have a network F granting the ability to open network connections and read from them, and so on.
13.4.3. Pure interpreters
Note that nothing about the ConsoleIO type implies that any effects must actually occur! That decision is the responsibility of the interpreter. We could choose to translate our Console actions into pure values that perform no I/O at all! For example, an interpreter for testing purposes could just ignore PrintLine requests and always return a constant string in response to ReadLine requests. We do this by translating our Console requests to a String => A, which forms a monad in A, as we saw in chapter 11, exercise 11.20 (readerMonad).
Listing 13.7. Creating our ConsoleReader class

We introduce another function on Console, toReader, and then use that to implement runConsoleReader:
sealed trait Console[A] {
...
def toReader: ConsoleReader[A]
}
val consoleToReader = new (Console ~> ConsoleReader) {
def apply[A](a: Console[A]) = a.toReader
}
@annotation.tailrec
def runConsoleReader[A](io: ConsoleIO[A]): ConsoleReader[A] =
runFree[Console,ConsoleReader,A](io)(consoleToReader)
Or for a more complete simulation of console I/O, we could write an interpreter that uses two lists—one to represent the input buffer and another to represent the output buffer. When the interpreter encounters a ReadLine, it can pop an element off the input buffer, and when it encounters aPrintLine(s), it can push s onto the output buffer:
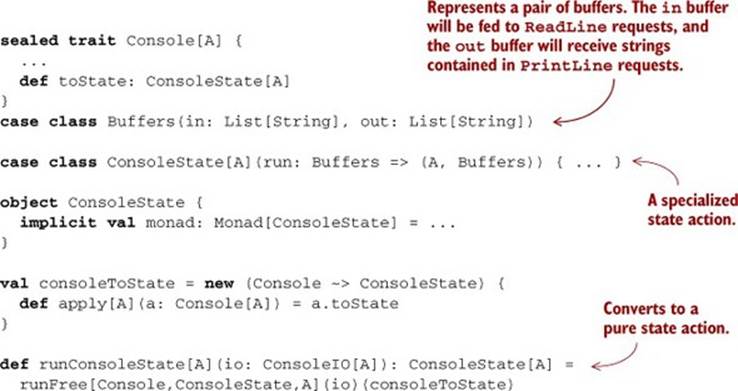
This will allow us to have multiple interpreters for our little languages! We could, for example, use runConsoleState for testing console applications with our property-based testing library from chapter 8, and then use runConsole to run our program for real.[13]
13 Note that runConsoleReader and runConsoleState aren’t stack-safe as implemented, for the same reason that runConsoleFunction0 wasn’t stack-safe. We can fix this by changing the representations to String => TailRec[A] for ConsoleReader and Buffers => TailRec[(A,Buffers)] for ConsoleState.
The fact that we can write a generic runFree that turns Free programs into State or Reader values demonstrates something amazing—there’s nothing about our Free type that requires side effects of any kind. For example, from the perspective of our ConsoleIO programs, we can’t know (and don’t care) whether they’re going to be run with an interpreter that uses “real” side effects like runConsole, or one like runConsoleState that doesn’t. As far as we’re concerned, a program is just a referentially transparent expression—a pure computation that may occasionally make requests of some interpreter. The interpreter is free to use side effects or not. That’s now an entirely separate concern.
13.5. Non-blocking and asynchronous I/O
Let’s turn our attention now to the last remaining problem with our original IO monad—that of performing non-blocking or asynchronous I/O. When performing I/O, we frequently need to invoke operations that take a long time to complete and don’t occupy the CPU. These include accepting a network connection from a server socket, reading a chunk of bytes from an input stream, writing a large number of bytes to a file, and so on. Let’s think about what this means in terms of the implementation of our Free interpreter.
When runConsole, for example, encounters a Suspend(s), s will be of type Console and we’ll have a translation f from Console to the target monad. To allow for non-blocking asynchronous I/O, we simply change the target monad from Function0 to Par or another concurrency monad such as scala.concurrent.Future. So just like we were able to write both pure and effectful interpreters for Console, we can write both blocking and non-blocking interpreters as well, just by varying the target monad.[14]
14 Our Par monad from chapter 7 doesn’t do any handling of exceptions. See the file Task.scala in the answer source code accompanying this chapter for an example of an asynchronous I/O monad with proper exception handling.
Let’s look at an example. Here, runConsolePar will turn the Console requests into Par actions and then combine them all into one Par[A]. We can think of it as a kind of compilation—we’re replacing the abstract Console requests with more concrete Par requests that will actually read from and write to the standard input and output streams when the resulting Par value is run:
scala> def p: ConsoleIO[Unit] = for {
| _ <- printLn("What's your name?")
| n <- readLn
| _ <- n match {
| case Some(n) => printLn(s"Hello, $n!")
| case None => printLn(s"Fine, be that way.")
| }
| } yield ()
p: ConsoleIO[Unit] =
FlatMap(Suspend(PrintLine(What's your name?)),<function1>)
scala> val q = runConsolePar(p)
q: Par[Unit] = <function1>
Although this simple example runs in Par, which in principle permits asynchronous actions, it doesn’t make use of any asynchronous actions—readLine and println are both blocking I/O operations. But there are I/O libraries that support non-blocking I/O directly and Par will let us bind to such libraries. The details of these libraries vary, but to give the general idea, a non-blocking source of bytes might have an interface like this:
trait Source {
def readBytes(
numBytes: Int,
callback: Either[Throwable, Array[Byte]] => Unit): Unit
}
Here it’s assumed that readBytes returns immediately. We give readBytes a callback function indicating what to do when the result becomes available or the I/O subsystem encounters an error.
Obviously, using this sort of library directly is painful.[15] We want to program against a compositional monadic interface and abstract over the details of the underlying non-blocking I/O library. Luckily, the Par type lets us wrap these callbacks:
15 Even this API is rather nicer than what’s offered directly by the nio package in Java (API at http://mng.bz/uojM), which supports non-blocking I/O.
trait Future[+A] {
private def apply(k: A => Unit): Unit
}
type Par[+A] = ExecutorService => Future[A]
The internal representation of Future is remarkably similar to that of Source. It’s a single method that returns immediately, but takes a callback or continuation k that it will invoke once the value of type A becomes available. It’s straightforward to wrap Source.readBytes in a Future, but we’ll need to add a primitive to our Par algebra:[16]
16 This may in fact be the most primitive Par operation. The other primitives we developed for Par in chapter 7 could be implemented in terms of this one.
def async[A](run: (A => Unit) => Unit): Par[A] = es => new Future {
def apply(k: A => Unit) = run(k)
}
With this in place, we can now wrap the asynchronous readBytes function in the nice monadic interface of Par:
def nonblockingRead(source: Source, numBytes: Int):
Par[Either[Throwable,Array[Byte]]] =
async { (cb: Either[Throwable,Array[Byte]] => Unit) =>
source.readBytes(numBytes, cb)
}
def readPar(source: Source, numBytes: Int):
Free[Par,Either[Throwable,Array[Byte]]] =
Suspend(nonblockingRead(source, numBytes))
And we can now use regular for-comprehensions to construct chains of non-blocking computations:
val src:Source = ...
val prog: Free[Par,Unit] = for {
chunk1<- readPar(src, 1024)
chunk2<- readPar(src, 1024)
...
}
Exercise 13.5
![]()
Hard: We’re not going to work through a full-fledged implementation of a non-blocking I/O library here, but you may be interested to explore this on your own by building off the java.nio library (API at http://mng.bz/uojM). As a start, try implementing an asynchronous read from anAsynchronousFileChannel (API at http://mng.bz/X30L).[17]
17 This requires Java 7 or better.
def read(file: AsynchronousFileChannel,
fromPosition: Long,
numBytes: Int): Par[Either[Throwable, Array[Byte]]]
13.6. A general-purpose IO type
We can now formulate a general methodology of writing programs that perform I/O. For any given set of I/O operations that we want to support, we can write an algebraic data type whose case classes represent the individual operations. For example, we could have a Files data type for file I/O, a DB data type for database access, and use something like Console for interacting with standard input and output. For any such data type F, we can generate a free monad Free[F,A] in which to write our programs. These can be tested individually and then finally “compiled” down to a lower-level I/O type, what we earlier called Async:
type IO[A] = Free[Par, A]
This IO type supports both trampolined sequential execution (because of Free) and asynchronous execution (because of Par). In our main program, we bring all of the individual effect types together under this most general type. All we need is a translation from any given F to Par.
13.6.1. The main program at the end of the universe
When the JVM calls into our main program, it expects a main method with a specific signature. The return type of this method is Unit, meaning that it’s expected to have some side effects. But we can delegate to a pureMain program that’s entirely pure! The only thing the main method does in that case is interpret our pure program, actually performing the effects.
Listing 13.8. Turning side effects into just effects

We want to make a distinction here between effects and side effects. The pureMain program itself isn’t going to have any side effects. It should be a referentially transparent expression of type IO[Unit]. The performing of effects is entirely contained within main, which is outside the universe of our actual program, pureMain. Since our program can’t observe these effects occurring, but they nevertheless occur, we say that our program has effects but not side effects.
13.7. Why the IO type is insufficient for streaming I/O
Despite the flexibility of the IO monad and the advantage of having I/O actions as first-class values, the IO type fundamentally provides us with the same level of abstraction as ordinary imperative programming. This means that writing efficient, streaming I/O will generally involve monolithic loops.
Let’s look at an example. Suppose we wanted to write a program to convert a file, fahrenheit.txt, containing a sequence of temperatures in degrees Fahrenheit, separated by line breaks, to a new file, celsius.txt, containing the same temperatures in degrees Celsius. An algebra for this might look something like this:[18]
18 We’re ignoring exception handling in this API.
trait Files[A]
case class ReadLines(file: String) extends Files[List[String]]
case class WriteLines(file: String, lines: List[String])
extends Files[Unit]
Using this as our F type in Free[F,A], we might try to write the program we want in the following way:
val p: Free[Files,Unit] = for {
lines <- Suspend { (ReadLines("fahrenheit.txt")) }
cs = lines.map(s => fahrenheitToCelsius(s.toDouble).toString)
_ <- Suspend { WriteLines("celsius.txt", cs) }
} yield ()
This works, although it requires loading the contents of fahrenheit.txt entirely into memory to work on it, which could be problematic if the file is very large. We’d prefer to perform this task using roughly constant memory—read a line or a fixed-size buffer full of lines fromfarenheit.txt, convert to Celsius, dump to celsius.txt, and repeat. To achieve this efficiency we could expose a lower-level file API that gives access to I/O handles:
trait Files[A]
case class OpenRead(file: String) extends Files[HandleR]
case class OpenWrite(file: String) extends Files[HandleW]
case class ReadLine(h: HandleR) extends Files[Option[String]]
case class WriteLine(h: HandleW, line: String) extends Files[Unit]
trait HandleR
trait HandleW
The only problem is that we now need to write a monolithic loop:
def loop(f: HandleR, c: HandleW): Free[Files, Unit] = for {
line <- Suspend { ReadLine(f) }
_ <- line match {
case None => IO.unit(())
case Some(s) => Suspend {
WriteLine(fahrenheitToCelsius(s.toDouble))
} flatMap (_ => loop(f, c))
}
} yield b
def convertFiles = for {
f <- Suspend(OpenRead("fahrenheit.txt"))
c <- Suspend(OpenWrite("celsius.txt"))
_ <- loop(f,c)
} yield ()
There’s nothing inherently wrong with writing a monolithic loop like this, but it’s not composable. Suppose we decide later that we’d like to compute a five-element moving average of the temperatures. Modifying our loop function to do this would be somewhat painful. Compare that to the equivalent change we might make to List-based code, where we could define a movingAvg function and just stick it before or after our conversion to Celsius:
def movingAvg(n: Int)(l: List[Double]): List[Double]
cs = movingAvg(5)(lines.map(s =>fahrenheitToCelsius(s.toDouble))).
map(_.toString)
Even movingAvg could be composed from smaller pieces—we could build it using a generic combinator, windowed:
def windowed[A](n: Int, l: List[A])(f: A => B)(m: Monoid[B]): List[B]
The point is that programming with a composable abstraction like List is much nicer than programming directly with the primitive I/O operations. Lists aren’t really special in this regard—they’re just one instance of a composable API that’s pleasant to use. And we shouldn’t have to give up all the nice compositionality that we’ve come to expect from FP just to write programs that make use of efficient, streaming I/O.[19] Luckily we don’t have to. As we’ll see in chapter 15, we get to build whatever abstractions we want for creating computations that perform I/O. If we like the metaphor of lists or streams, we can design a list-like API for expressing I/O computations. If we discover some other composable abstraction, we can find a way of using that instead. Functional programming gives us that flexibility.
19 One might ask if we could just have various Files operations return the Stream type we defined in chapter 5. This is called lazy I/O, and it’s problematic for several reasons we’ll discuss in chapter 15.
13.8. Summary
This chapter introduced a simple model for handling external effects and I/O in a purely functional way. We began with a discussion of factoring effects and demonstrated how effects can be moved to the outer layers of a program. We generalized this to an IO data type that lets us describe interactions with the outside world without resorting to side effects.
We discovered that monads in Scala suffer from a stack overflow problem, and we solved it in a general way using the technique of trampolining. This led us to the even more general idea of free monads, which we employed to write a very capable IO monad with an interpreter that used non-blocking asynchronous I/O internally.
The IO monad is not the final word in writing effectful programs. It’s important because it represents a kind of lowest common denominator when interacting with the external world. But in practice, we want to use IO directly as little as possible because IO programs tend to be monolithic and have limited reuse. In chapter 15, we’ll discuss how to build nicer, more composable, more reusable abstractions using essentially the same technique that we used here.
Before getting to that, we’ll apply what we’ve learned so far to fill in the other missing piece of the puzzle: local effects. At various places throughout this book, we’ve made use of local mutation rather casually, with the assumption that these effects weren’t observable. In the next chapter, we’ll explore what this means in more detail, see more examples of using local effects, and show how effect scoping can be enforced by the type system.