Functional Python Programming (2015)
Chapter 13. Conditional Expressions and the Operator Module
Functional programming emphasizes lazy or non-strict ordering of operations. The idea is to allow the compiler or runtime to do as little work as possible to compute the answer. Python tends to impose strict ordering on evaluations.
For example, we used the Python if, elif, and else statements. They're clear and readable, but they imply a strict ordering on the evaluation of the conditions. We can, to an extent, free ourselves from the strict ordering here, and develop a limited kind of non-strict conditional statement. It's not clear if this is helpful but it shows some alternative ways to express an algorithm in a functional style.
The first part of this chapter will look at ways we can implement non-strict evaluation. This is a tool that's interesting because it can lead to performance optimizations.
In the previous chapters, we looked at a number of higher-order functions. In some cases, we used these higher-order functions to apply fairly sophisticated functions to collections of data. In other cases, we applied simple functions to collections of data.
Indeed, in many cases, we wrote tiny lambda objects to apply a single Python operator to a function. For example, we can use the following to define a prod() function:
>>> prod= lambda iterable: functools.reduce(lambda x, y: x*y, iterable, 1)
>>> prod((1,2,3))
6
The use of the lambda x,y: x*y parameter seems a bit wordy for multiplication. After all, we just want to use the multiplication operator, *. Can we simplify the syntax? The answer is yes; the operator module provides us with definitions of the built-in operators.
There are a number of features of the operator module that lead to some simplification and potential clarification to create higher-order functions. While important conceptually, the operator module isn't as interesting as it initially appears.
Evaluating conditional expressions
Python imposes relatively strict ordering on expressions; the notable exceptions are the short-circuit operators, and and or. It imposes very strict ordering on statement evaluation. This makes it challenging to find different ways to avoid this strict evaluation.
It turns out that evaluating condition expressions is one way in which we can experiment with non-strict ordering of statements. We'll examine some ways to refactor the if and else statements to explore this aspect of non-strict evaluation in Python.
The Python if, elif, and else statements are evaluated in a strict order from first to last. Ideally, a language might relax this rule so that an optimizing compiler can find a faster order for evaluating the conditional expressions. The idea is for us to write the expressions in an order that makes sense to a reader, even if the actual evaluation order is non-strict.
Lacking an optimizing compiler, this concept is a bit of a stretch for Python. Nonetheless, we do have alternative ways to express conditions that involve the evaluation of functions instead of the execution of imperative statements. This can allow you to make some rearrangement at runtime.
Python does have a conditional if and else expression. This expression form can be used when there's a single condition. When we have multiple conditions, however, it can get awkwardly complex: we'd have to carefully nest the subexpressions. We might wind up with a command, as follows, which is rather difficult to comprehend:
(x if n==1 else (y if n==2 else z))
We can use dictionary keys and the lambda objects to create a very complex set of conditions. Here's a way to express the factorial function as expressions:
def fact(n):
f= { n == 0: lambda n: 1,
n == 1: lambda n: 1,
n == 2: lambda n: 2,
n > 2: lambda n: fact(n-1)*n }[True]
return f(n)
This rewrites the conventional if, elif, elif, and else sequence of statements into a single expression. We've decomposed it into two steps to make what's happening slightly clearer.
In the first step, we'll evaluate the various conditions. One of the given conditions will evaluate to True, the others should all evaluate to False. The resulting dictionary will have two items in it: a True key with a lambda object and a False key with a lambda object. We'll select the True item and assign it to the f variable.
We used lambdas as the values in this mapping so that the value expressions aren't evaluated when the dictionary is built. We want to evaluate just one of the value expressions. The return statement evaluates the one expression associated with the True condition.
Exploiting non-strict dictionary rules
A dictionary's keys have no order. If we try to create a dictionary with multiple items that share a common key value, we'll only have one item in the resulting dict object. It's not clear which of the duplicated key values will be preserved, and it shouldn't matter.
Here's a situation where we explicitly don't care which of the duplicated keys is preserved. We'll look at a degenerate case of the max() function, it simply picks the largest of two values:
def max(a, b):
f = {a >= b: lambda: a, b >= a: lambda: b}[True]
return f()
In the case where a == b, both items in the dictionary will have a key of the True condition. Only one of the two will actually be preserved. Since the answer is the same, it doesn't matter which is kept and which is treated as a duplicate and overwritten.
Filtering true conditional expressions
We have a number of ways of determining which expression is True. In the previous example, we loaded the keys into a dictionary. Because of the way the dictionary is loaded, only one value will be preserved with a key of True.
Here's another variation to this theme, written using the filter() function:
def semifact(n):
alternatives= [(n == 0, lambda n: 1),
(n == 1, lambda n: 1),
(n == 2, lambda n: 2),
(n > 2, lambda n: semifact(n-2)*n)]
c, f= next(filter(itemgetter(0), alternatives))
return f(n)
We defined the alternatives as a sequence of condition and function pairs. When we apply the filter() function using the itemgetter(0) parameter, we'll select those pairs with a True condition. Of those which are True, we'll select the first item in the iterable created by the filter() function. The selected condition is assigned to the c variable, the selected function is assigned to the f variable. We can ignore the condition (it will be True), and we can evaluate the filter() function.
As with the previous example, we used lambdas to defer evaluation of the functions until after the conditions have been evaluated.
This semifact() function is also called double factorial. The definition of the semifactorial is similar to the definition of factorial. The important difference is that it is the product of alternate numbers instead of all numbers. For example, take a look at the following formulas:
![]() , and
, and ![]()
Using the operator module instead of lambdas
When using the max(), min(), and sorted() functions, we have an optional key= parameter. The function provided as an argument value modifies the behavior of the higher-order function. In many cases, we used simple lambda forms to pick items from a tuple. Here are two examples we heavily relied on:
fst = lambda x: x[0]
snd = lambda x: x[1]
These match built-in functions in other functional programming languages.
We don't really need to write these functions. There's a version available in the operator module which describes these functions.
Here's some sample data we can work with:
>>> year_cheese = [(2000, 29.87), (2001, 30.12), (2002, 30.6), (2003, 30.66), (2004, 31.33), (2005, 32.62), (2006, 32.73), (2007, 33.5), (2008, 32.84), (2009, 33.02), (2010, 32.92)]
This is the annual cheese consumption. We used this example in Chapter 2, Introducing Some Functional Features and Chapter 9, More Itertools Techniques.
We can locate the data point with minimal cheese using the following commands:
>>> min(year_cheese, key=snd)
(2000, 29.87)
The operator module gives us an alternative to pick particular elements from a tuple. This saves us from using a lambda variable to pick the second item.
Instead of defining our own fst() and snd() functions, we can use the itemgetter(0) and the itemgetter(1) parameters, as shown in the following command:
>>> from operator import *
>>> max( year_cheese, key=itemgetter(1))
(2007, 33.5)
The itemgetter() function relies on the special method, __getitem__(), to pick items out of a tuple (or list) based on their index position.
Getting named attributes when using higher-order functions
Let's look at a slightly different collection of data. Let's say we were working with namedtuples instead of anonymous tuples. We have two ways to locate the range of cheese consumption shown as follows:
>>> from collections import namedtuple
>>> YearCheese = namedtuple("YearCheese", ("year", "cheese"))
>>> year_cheese_2 = list(YearCheese(*yc) for yc in year_cheese)
>>> year_cheese_2
[YearCheese(year=2000, cheese=29.87), YearCheese(year=2001, cheese=30.12), YearCheese(year=2002, cheese=30.6), YearCheese(year=2003, cheese=30.66), YearCheese(year=2004, cheese=31.33), YearCheese(year=2005, cheese=32.62), YearCheese(year=2006, cheese=32.73), YearCheese(year=2007, cheese=33.5), YearCheese(year=2008, cheese=32.84), YearCheese(year=2009, cheese=33.02), YearCheese(year=2010, cheese=32.92)]
We can use lambda forms or we can use the attrgetter() function, as follows:
>>> min(year_cheese_2, key=attrgetter('cheese'))
YearCheese(year=2000, cheese=29.87)
>>> max(year_cheese_2, key=lambda x: x.cheese)
YearCheese(year=2007, cheese=33.5)
What's important here is that with a lambda object, the attribute name is expressed as a token in the code. With the attrgetter() function, the attribute name is a character string. This could be a parameter, which allows us to be considerably flexible.
Starmapping with operators
The itertools.starmap() function can be applied to an operator and a sequence of pairs of values. Here's an example:
>>> d= starmap(pow, zip_longest([], range(4), fillvalue=60))
The itertools.zip_longest() function will create a sequence of pairs such as the following:
[(60, 0), (60, 1), (60, 2), (60, 3)]
It does this because we provided two sequences: the [] brackets and the range(4) parameter. The fillvalue parameter will be used when the shorter sequence runs out of data.
When we use the starmap() function, each pair becomes the argument to the given function. In this case, we provided the operator.pow() function, which is the ** operator. We've calculated values for [60**0, 60**1, 60**2, 60**3]. The value of the d variable is [1, 60, 3600, 216000].
The starmap() function is useful when we have a sequence of tuples. We have a tidy equivalence between the map(f, x, y) and starmap(f, zip(x,y)) functions.
Here's a continuation of the preceding example of the itertools.starmap() function:
>>> p = (3, 8, 29, 44)
>>> pi = sum(starmap(truediv, zip(p, d)))
We've zipped together two sequences of four values. We used the starmap() function with the operator.truediv() function, which is the / operator. This will compute a sequence of fractions that we sum. The sum is really an approximation of ![]()
Here's a simpler version that uses the map(f, x, y) function instead of the starmap(f, zip(x,y)) function:
>>> pi = sum(map(truediv, p, d))
>>> pi
3.1415925925925925
In this example, we effectively converted a base 60 fractional value to base 10. The sequence of values in the d variable are the appropriate denominators. A technique similar to the one explained earlier in this section can be used to convert other bases.
Some approximations involve potentially infinite sums (or products). These can be evaluated using similar techniques explained previously in this section. We can leverage the count() function in the itertools module to generate an arbitrary number of terms in an approximation. We can then use the takewhile() function to only use values that contribute a useful level of precision to the answer.
Here's an example of a potentially infinite sequence:
>>> num= map(fact, count())
>>> den= map(semifact, (2*n+1 for n in count()))
>>> terms= takewhile(lambda t: t > 1E-10, map(truediv, num, den))
>>> 2*sum(terms)
3.1415926533011587
The num variable is a potentially infinite sequence of numerators, based on a factorial function. The den variable is a potentially infinite sequence of denominators, based on the semifactorial (sometimes called the double factorial) function.
To create terms, we used the map() function to apply the operators.truediv() function, the / operator, to each pair of values. We wrapped this in a takewhile() function so that we only take values while the fraction is greater than some relatively small value; in this case, ![]() .
.
This is a series expansion based on 4 arctan(1)=![]() . The expansion is
. The expansion is 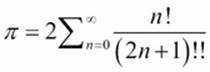
An interesting variation to the series expansion theme is to replace the operator.truediv() function with the fractions.Fraction() function. This will create exact rational values that don't suffer from the limitations of floating-point approximations.
All of the Python operators are available in the operators module. This includes all of the bit-fiddling operators as well as the comparison operators. In some cases, a generator expression may be more succinct or expressive than a rather complex-looking starmap()function with a function that represents an operator.
The issue is that the operator module provides only a single operator, essentially a shorthand for lambda. We can use the operator.add method instead of the add=lambda a,b: a+b method. If we have more complex expressions, then the lambda object is the only way to write them.
Reducing with operators
We'll look at one more way that we might try to use the operator definitions. We can use them with the built-in functools.reduce() function. The sum() function, for example, can be defined as follows:
sum= functools.partial(functools.reduce, operator.add)
We created a partially evaluated version of the reduce() function with the first argument supplied. In this case, it's the + operator, implemented via the operator.add() function.
If we have a requirement for a similar function that computes a product, we can define it like this:
prod= functools.partial(functools.reduce, operator.mul)
This follows the pattern shown in the preceding example. We have a partially evaluated reduce() function with the first argument of * operator, as implemented by the operator.mul() function.
It's not clear whether we can do similar things with too many of the other operators. We might be able to find a use for the operator.concat() function as well as the operator.and() and operator.or() functions.
Note
The and() and or() functions are the bit-wise & and / operators. If we want the proper Boolean operators, we have to use the all() and any() functions instead of the reduce() function.
Once we have a prod() function, this means that the factorial can be defined as follows:
fact= lambda n: 1 if n < 2 else n*prod(range(1,n))
This has the advantage of being succinct: it provides a single line definition of factorial. It also has the advantage of not relying on recursion but has the potential of running afoul Python's stack limit.
It's not clear that this has any dramatic advantages over the many alternatives we have in Python. The concept of building a complex function from primitive pieces like the partial() and reduce() functions, and the operator module is very elegant. In most cases, though, the simple functions in the operator module aren't very helpful; we'll almost always want to use more complex lambdas.
Summary
In this chapter, we looked at alternatives to the if, elif, and else statement sequence. Ideally, using a conditional expression allows some optimization to be done. Pragmatically, Python doesn't optimize, so there's little tangible benefit to the more exotic ways to handle conditions.
We also looked at how we can use the operator module with higher order functions like max(), min(), sorted(), and reduce(). Using operators can save us from having to create a number of small lambdas.
In the next chapter, we'll look at the PyMonad library to express a functional programming concept directly in Python. We don't require monads generally because Python is an imperative programming language under the hood.
Some algorithms might be expressed more clearly with monads than with stateful variable assignments. We'll look at an example where monads lead to a succinct expression of a rather complex set of rules. Most importantly, the operator module shows off many functional programming techniques.