Data Science from Scratch: First Principles with Python (2015)
Chapter 10. Working with Data
Experts often possess more data than judgment.
Colin Powell
Exploring Your Data
Exploring One-Dimensional Data
defbucketize(point,bucket_size):
"""floor the point to the next lower multiple of bucket_size"""
returnbucket_size*math.floor(point/bucket_size)
defmake_histogram(points,bucket_size):
"""buckets the points and counts how many in each bucket"""
returnCounter(bucketize(point,bucket_size)forpointinpoints)
defplot_histogram(points,bucket_size,title=""):
histogram=make_histogram(points,bucket_size)
plt.bar(histogram.keys(),histogram.values(),width=bucket_size)
plt.title(title)
plt.show()
random.seed(0)# uniform between -100 and 100uniform=[200*random.random()-100for_inrange(10000)]
# normal distribution with mean 0, standard deviation 57normal=[57*inverse_normal_cdf(random.random())
for_inrange(10000)]
plot_histogram(uniform,10,"Uniform Histogram")
plot_histogram(normal,10,"Normal Histogram")
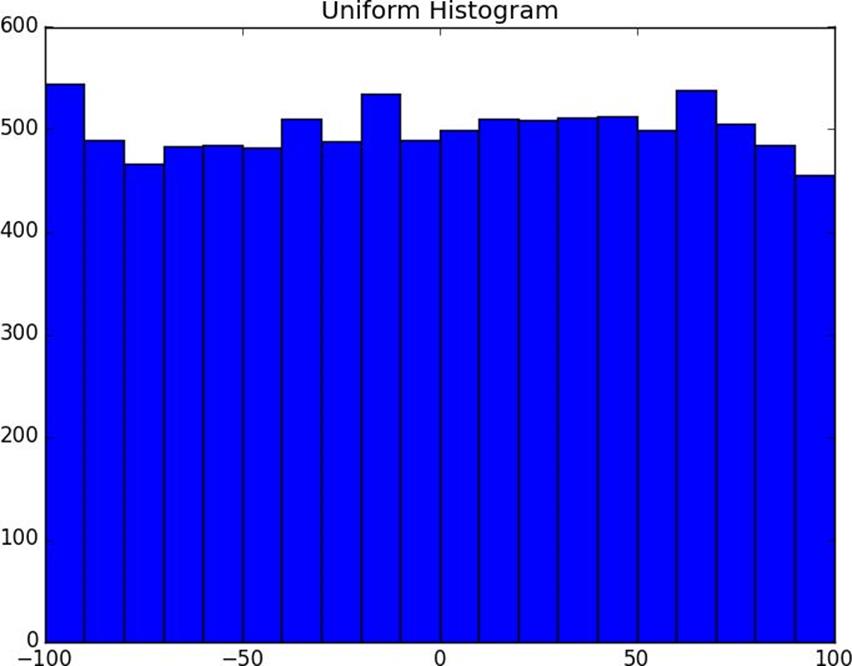
Figure 10-1. Histogram of uniform
defrandom_normal():
"""returns a random draw from a standard normal distribution"""
returninverse_normal_cdf(random.random())
xs=[random_normal()for_inrange(1000)]
ys1=[x+random_normal()/2forxinxs]
ys2=[-x+random_normal()/2forxinxs]
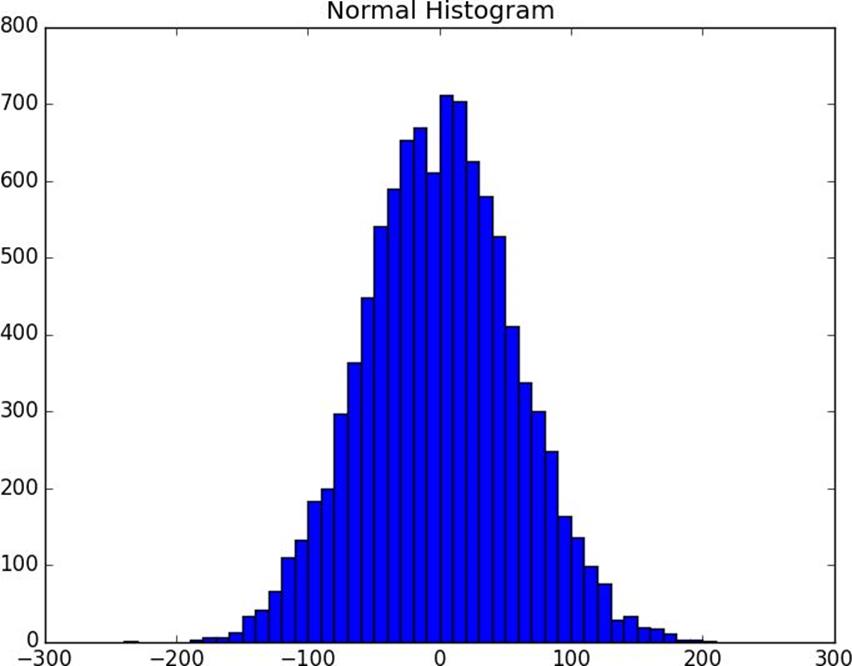
Figure 10-2. Histogram of normal
plt.scatter(xs,ys1,marker='.',color='black',label='ys1')
plt.scatter(xs,ys2,marker='.',color='gray',label='ys2')
plt.xlabel('xs')plt.ylabel('ys')plt.legend(loc=9)plt.title("Very Different Joint Distributions")plt.show()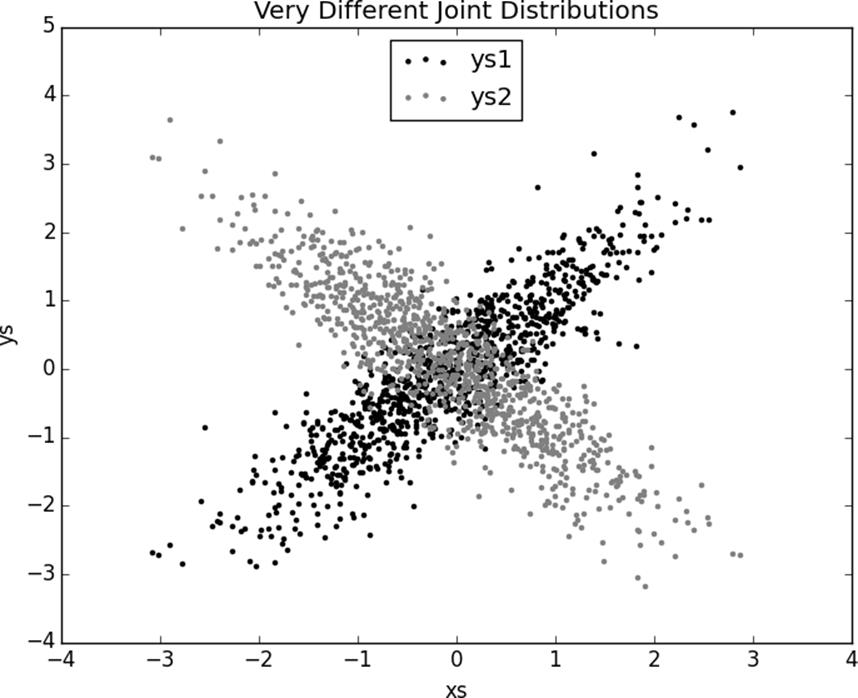
Figure 10-3. Scattering two different ys
correlation(xs,ys1)# 0.9
correlation(xs,ys2)# -0.9
Many Dimensions
defcorrelation_matrix(data):
"""returns the num_columns x num_columns matrix whose (i, j)th entry
is the correlation between columns i and j of data"""_,num_columns=shape(data)
defmatrix_entry(i,j):
returncorrelation(get_column(data,i),get_column(data,j))
returnmake_matrix(num_columns,num_columns,matrix_entry)
importmatplotlib.pyplotasplt
_,num_columns=shape(data)
fig,ax=plt.subplots(num_columns,num_columns)
foriinrange(num_columns):
forjinrange(num_columns):
# scatter column_j on the x-axis vs column_i on the y-axis
ifi!=j:ax[i][j].scatter(get_column(data,j),get_column(data,i))
# unless i == j, in which case show the series name
else:ax[i][j].annotate("series "+str(i),(0.5,0.5),
xycoords='axes fraction',
ha="center",va="center")
# then hide axis labels except left and bottom charts
ifi<num_columns-1:ax[i][j].xaxis.set_visible(False)
ifj>0:ax[i][j].yaxis.set_visible(False)
# fix the bottom right and top left axis labels, which are wrong because# their charts only have text in themax[-1][-1].set_xlim(ax[0][-1].get_xlim())ax[0][0].set_ylim(ax[0][1].get_ylim())plt.show()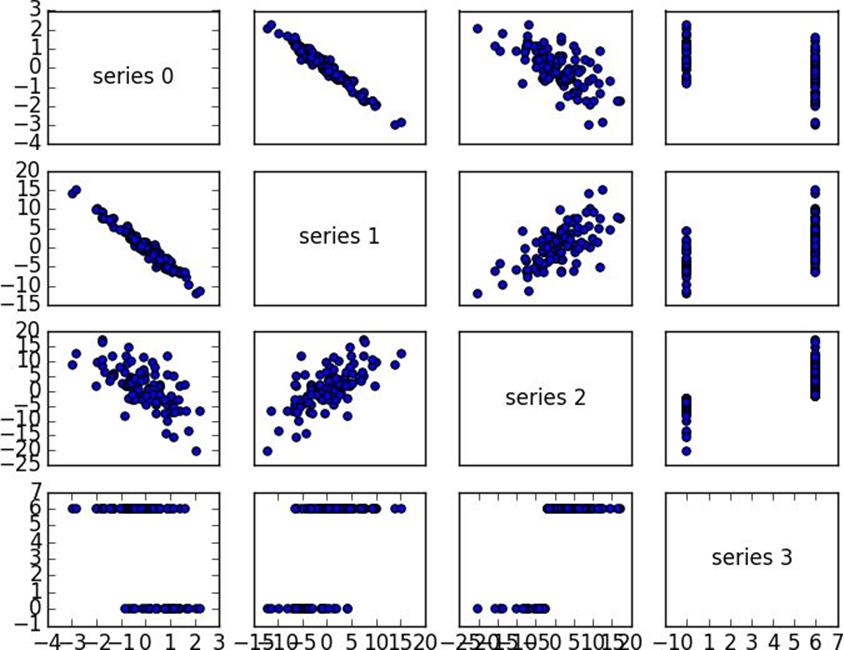
Figure 10-4. Scatterplot matrix
closing_price=float(row[2])
defparse_row(input_row,parsers):
"""given a list of parsers (some of which may be None)
apply the appropriate one to each element of the input_row"""return[parser(value)ifparserisnotNoneelsevalue
forvalue,parserinzip(input_row,parsers)]
defparse_rows_with(reader,parsers):
"""wrap a reader to apply the parsers to each of its rows"""
forrowinreader:
yieldparse_row(row,parsers)
deftry_or_none(f):
"""wraps f to return None if f raises an exception
assumes f takes only one input"""deff_or_none(x):
try:returnf(x)
except:returnNone
returnf_or_none
defparse_row(input_row,parsers):
return[try_or_none(parser)(value)ifparserisnotNoneelsevalue
forvalue,parserinzip(input_row,parsers)]
6/20/2014,AAPL,90.916/20/2014,MSFT,41.686/20/3014,FB,64.56/19/2014,AAPL,91.866/19/2014,MSFT,n/a6/19/2014,FB,64.34importdateutil.parser
data=[]
withopen("comma_delimited_stock_prices.csv","rb")asf:
reader=csv.reader(f)
forlineinparse_rows_with(reader,[dateutil.parser.parse,None,float]):
data.append(line)
forrowindata:
ifany(xisNoneforxinrow):
row
deftry_parse_field(field_name,value,parser_dict):
"""try to parse value using the appropriate function from parser_dict"""
parser=parser_dict.get(field_name)# None if no such entry
ifparserisnotNone:
returntry_or_none(parser)(value)
else:
returnvalue
defparse_dict(input_dict,parser_dict):
return{field_name:try_parse_field(field_name,value,parser_dict)
forfield_name,valueininput_dict.iteritems()}
Manipulating Data
data=[
{'closing_price':102.06,
'date':datetime.datetime(2014,8,29,0,0),
'symbol':'AAPL'},
# ...
]1. Restrict ourselves to AAPL rows.
2. Grab the closing_price from each row.
3. Take the max of those prices.
max_aapl_price=max(row["closing_price"]
forrowindata
ifrow["symbol"]=="AAPL")
1. Group together all the rows with the same symbol.
2. Within each group, do the same as before:
# group rows by symbolby_symbol=defaultdict(list)
forrowindata:
by_symbol[row["symbol"]].append(row)
# use a dict comprehension to find the max for each symbolmax_price_by_symbol={symbol:max(row["closing_price"]
forrowingrouped_rows)
forsymbol,grouped_rowsinby_symbol.iteritems()}
defpicker(field_name):
"""returns a function that picks a field out of a dict"""
returnlambdarow:row[field_name]
defpluck(field_name,rows):
"""turn a list of dicts into the list of field_name values"""
returnmap(picker(field_name),rows)
defgroup_by(grouper,rows,value_transform=None):
# key is output of grouper, value is list of rows
grouped=defaultdict(list)
forrowinrows:
grouped[grouper(row)].append(row)
ifvalue_transformisNone:
returngrouped
else:
return{key:value_transform(rows)
forkey,rowsingrouped.iteritems()}
max_price_by_symbol=group_by(picker("symbol"),
data,
lambdarows:max(pluck("closing_price",rows)))
1. Order the prices by date.
2. Use zip to get pairs (previous, current).
3. Turn the pairs into new “percent change” rows.
defpercent_price_change(yesterday,today):
returntoday["closing_price"]/yesterday["closing_price"]-1
defday_over_day_changes(grouped_rows):
# sort the rows by date
ordered=sorted(grouped_rows,key=picker("date"))
# zip with an offset to get pairs of consecutive days
return[{"symbol":today["symbol"],
"date":today["date"],
"change":percent_price_change(yesterday,today)}
foryesterday,todayinzip(ordered,ordered[1:])]
# key is symbol, value is list of "change" dictschanges_by_symbol=group_by(picker("symbol"),data,day_over_day_changes)
# collect all "change" dicts into one big listall_changes=[change
forchangesinchanges_by_symbol.values()
forchangeinchanges]
max(all_changes,key=picker("change"))
# {'change': 0.3283582089552237,# 'date': datetime.datetime(1997, 8, 6, 0, 0),# 'symbol': 'AAPL'}# see, e.g. http://news.cnet.com/2100-1001-202143.htmlmin(all_changes,key=picker("change"))
# {'change': -0.5193370165745856,# 'date': datetime.datetime(2000, 9, 29, 0, 0),# 'symbol': 'AAPL'}# see, e.g. http://money.cnn.com/2000/09/29/markets/techwrap/# to combine percent changes, we add 1 to each, multiply them, and subtract 1# for instance, if we combine +10% and -20%, the overall change is# (1 + 10%) * (1 - 20%) - 1 = 1.1 * .8 - 1 = -12%defcombine_pct_changes(pct_change1,pct_change2):
return(1+pct_change1)*(1+pct_change2)-1
defoverall_change(changes):
returnreduce(combine_pct_changes,pluck("change",changes))
overall_change_by_month=group_by(lambdarow:row['date'].month,
all_changes,
overall_change)
|
Person |
Height (inches) |
Height (centimeters) |
Weight |
|
Table 10-1. Heights and Weights |
|||
a_to_b=distance([63,150],[67,160])# 10.77
a_to_c=distance([63,150],[70,171])# 22.14
b_to_c=distance([67,160],[70,171])# 11.40
a_to_b=distance([160,150],[170.2,160])# 14.28
a_to_c=distance([160,150],[177.8,171])# 27.53
b_to_c=distance([170.2,160],[177.8,171])# 13.37
defscale(data_matrix):
"""returns the means and standard deviations of each column"""
num_rows,num_cols=shape(data_matrix)
means=[mean(get_column(data_matrix,j))
forjinrange(num_cols)]
stdevs=[standard_deviation(get_column(data_matrix,j))
forjinrange(num_cols)]
returnmeans,stdevs
defrescale(data_matrix):
"""rescales the input data so that each column
has mean 0 and standard deviation 1 leaves alone columns with no deviation"""means,stdevs=scale(data_matrix)
defrescaled(i,j):
ifstdevs[j]>0:
return(data_matrix[i][j]-means[j])/stdevs[j]
else:
returndata_matrix[i][j]
num_rows,num_cols=shape(data_matrix)
returnmake_matrix(num_rows,num_cols,rescaled)
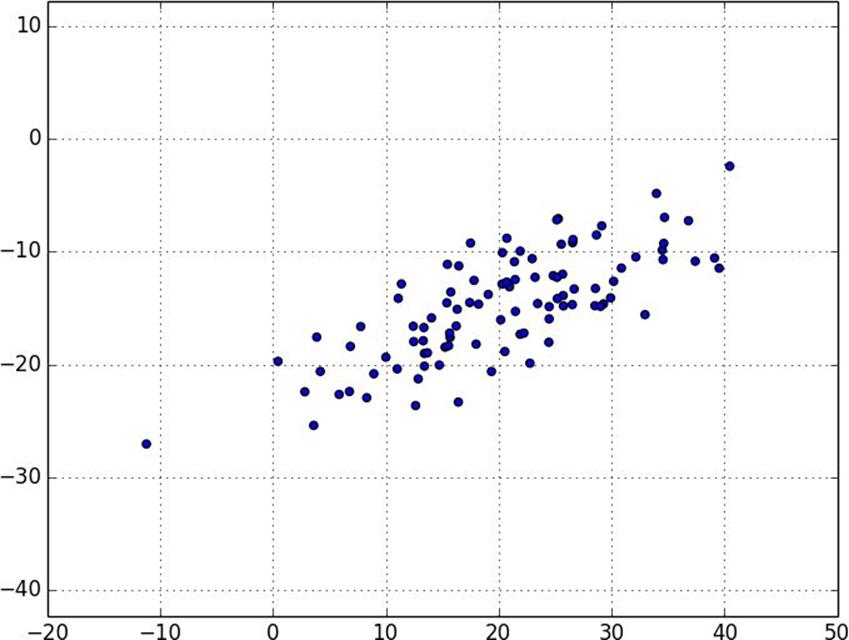
Figure 10-5. Data with the “wrong” axes
NOTE
defde_mean_matrix(A):
"""returns the result of subtracting from every value in A the mean
value of its column. the resulting matrix has mean 0 in every column"""nr,nc=shape(A)
column_means,_=scale(A)
returnmake_matrix(nr,nc,lambdai,j:A[i][j]-column_means[j])
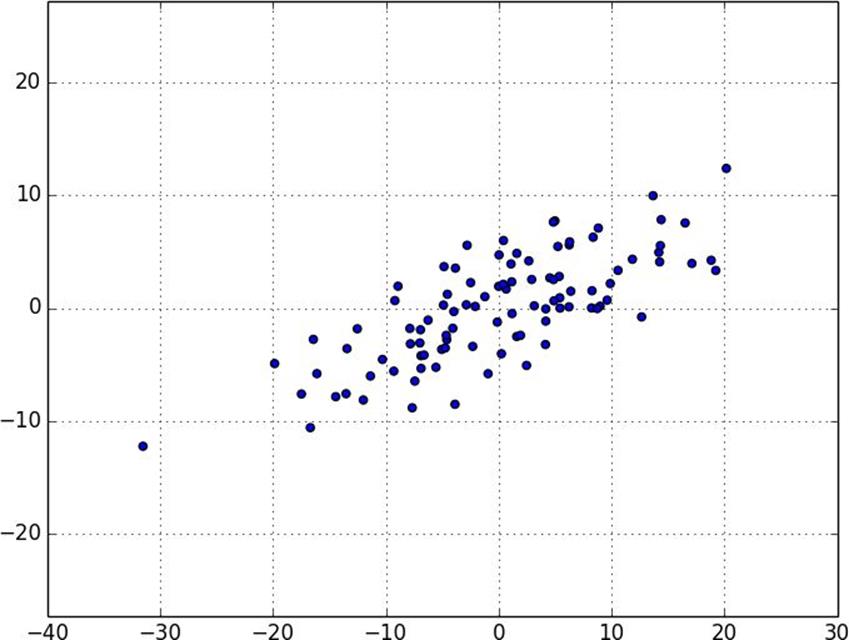
Figure 10-6. Data after de-meaning
defdirection(w):
mag=magnitude(w)
return[w_i/magforw_iinw]
defdirectional_variance_i(x_i,w):
"""the variance of the row x_i in the direction determined by w"""
returndot(x_i,direction(w))**2
defdirectional_variance(X,w):
"""the variance of the data in the direction determined w"""
returnsum(directional_variance_i(x_i,w)
forx_iinX)
defdirectional_variance_gradient_i(x_i,w):
"""the contribution of row x_i to the gradient of
the direction-w variance"""projection_length=dot(x_i,direction(w))
return[2*projection_length*x_ijforx_ijinx_i]
defdirectional_variance_gradient(X,w):
returnvector_sum(directional_variance_gradient_i(x_i,w)
forx_iinX)
deffirst_principal_component(X):
guess=[1for_inX[0]]
unscaled_maximizer=maximize_batch(
partial(directional_variance,X),# is now a function of w
partial(directional_variance_gradient,X),# is now a function of w
guess)
returndirection(unscaled_maximizer)
# here there is no "y", so we just pass in a vector of Nones# and functions that ignore that inputdeffirst_principal_component_sgd(X):
guess=[1for_inX[0]]
unscaled_maximizer=maximize_stochastic(
lambdax,_,w:directional_variance_i(x,w),
lambdax,_,w:directional_variance_gradient_i(x,w),
X,
[Nonefor_inX],# the fake "y"
guess)
returndirection(unscaled_maximizer)
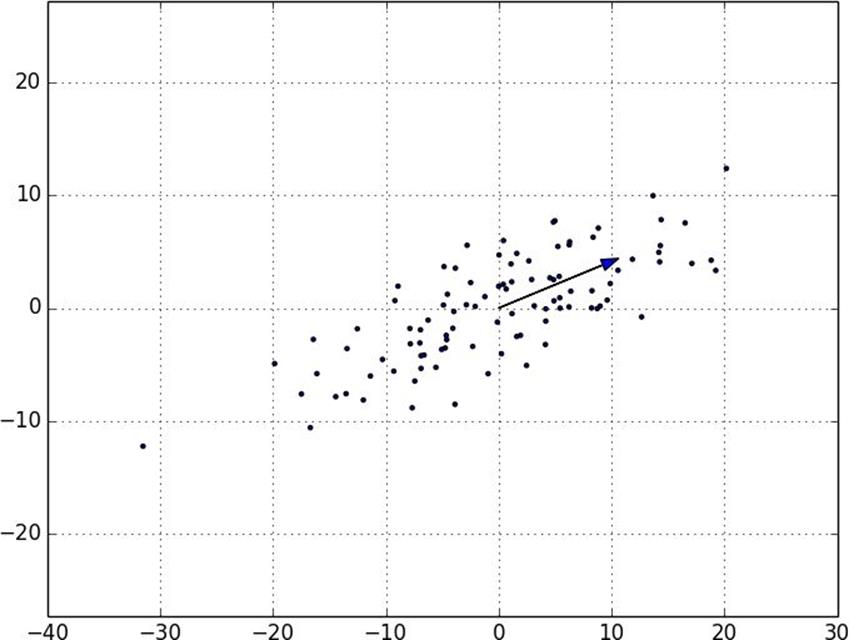
Figure 10-7. First principal component
defproject(v,w):
"""return the projection of v onto the direction w"""
projection_length=dot(v,w)
returnscalar_multiply(projection_length,w)
defremove_projection_from_vector(v,w):
"""projects v onto w and subtracts the result from v"""
returnvector_subtract(v,project(v,w))
defremove_projection(X,w):
"""for each row of X
projects the row onto w, and subtracts the result from the row"""return[remove_projection_from_vector(x_i,w)forx_iinX]
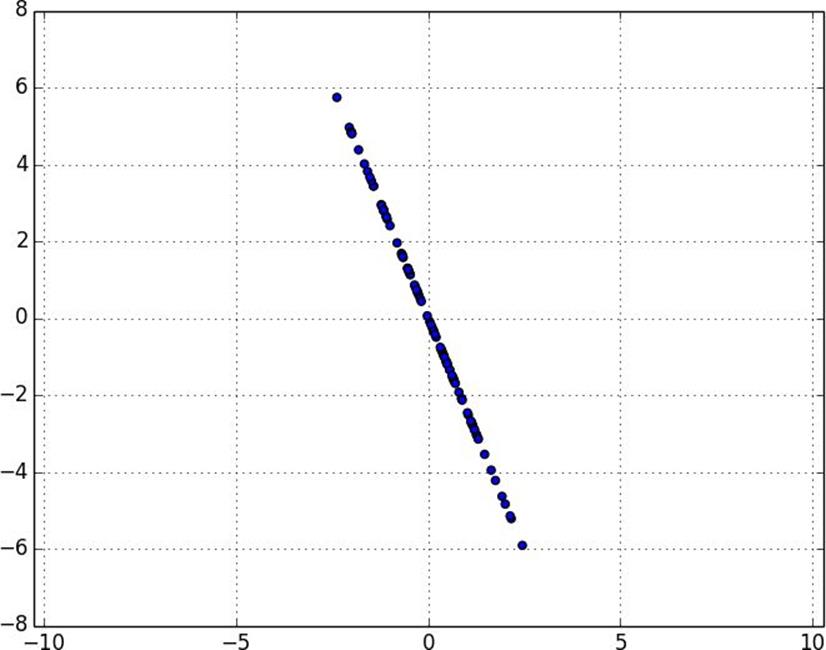
Figure 10-8. Data after removing first principal component
defprincipal_component_analysis(X,num_components):
components=[]
for_inrange(num_components):
component=first_principal_component(X)
components.append(component)
X=remove_projection(X,component)
returncomponents
deftransform_vector(v,components):
return[dot(v,w)forwincomponents]
deftransform(X,components):
return[transform_vector(x_i,components)forx_iinX]
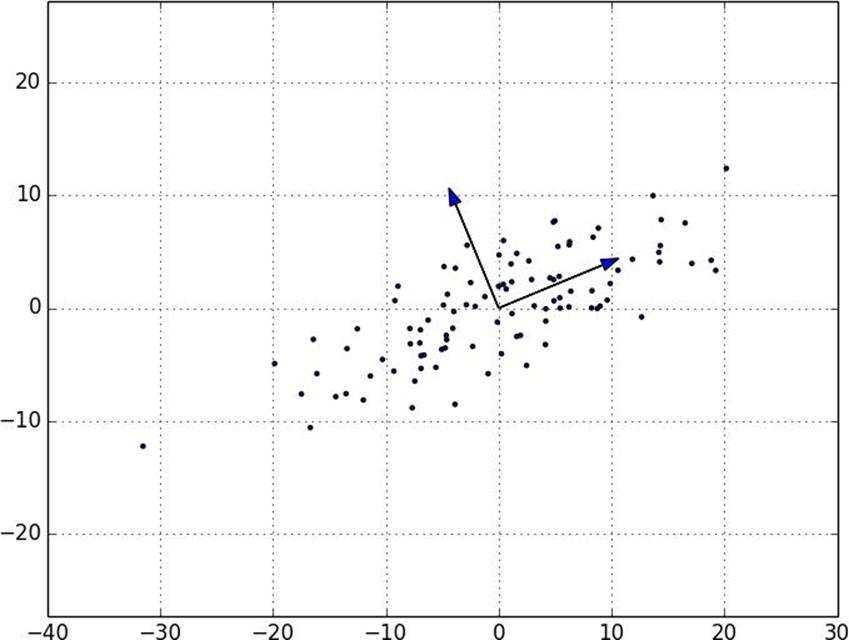
Figure 10-9. First two principal components
§ As we mentioned at the end of Chapter 9, pandas is probably the primary Python tool for cleaning, munging, manipulating, and working with data. All the examples we did by hand in this chapter could be done much more simply using pandas. Python for Data Analysis (O’Reilly) is probably the best way to learn pandas.
§ scikit-learn has a wide variety of matrix decomposition functions, including PCA.