Network Security Through Data Analysis: Building Situational Awareness (2014)

Part III. Analytics

In the previous two sections of the book, we’ve discussed the types of data you can collect, and tools for manipulating that data. In this section, we focus on taking that data and conducting analyses on that.

Each chapter in the following section focuses on a different family of mathematical and analytical techniques that can be used on data. The focus of each chapter is on providing information that is more security-relevant or floor-relevant. Chapter 10 focuses on the process of Exploratory Data Analysis (EDA), and should be read before anything else. Chapter 11, Chapter 12, Chapter 13, and Chapter 14 provide examples of behaviors, relate them to attacks, and discuss ways that these behaviors can be used to construct alarms or be used for forensics and investigation. Chapter 15looks at the problem of mapping a network, applying the techniques in the previous chapters to provide situational awareness.

Chapter 10. Exploratory Data Analysis and Visualization

Exploratory Data Analysis (EDA) is the process of examining a dataset without preconceived assumptions about the data and its behavior. Real-world datasets are messy and complex, and require progressive filtering and stratification in order to identify phenomena that are worth using for alarms, anomaly detection, and forensics. Attackers and the Internet itself are a moving target, and analysts face a constant influx of weirdness. For this reason, EDA is a constant process.

The point of EDA is to get a better grip on a dataset before pulling out the math. To understand why this is necessary, I want to walk through a simple statistical exercise. In Table 10-1, there are four datasets, each consisting of a vector X and a vector Y. For each dataset, calculate these values:

§ The mean of X and Y

§ The variance of X and Y

§ The correlation between X and Y

Table 10-1. Four datasets

You will find that the mean, variance, and correlation are identical for each dataset, but simply by looking at the numbers, you should suspect something fishy. A visualization will show just how diverse they are. Figure 10-1 plots these sets and shows how each dataset results in a radically different distribution. The Anscombe Quartet was designed to show the impact of outliers (such as in dataset IV) and visualization on data analysis.

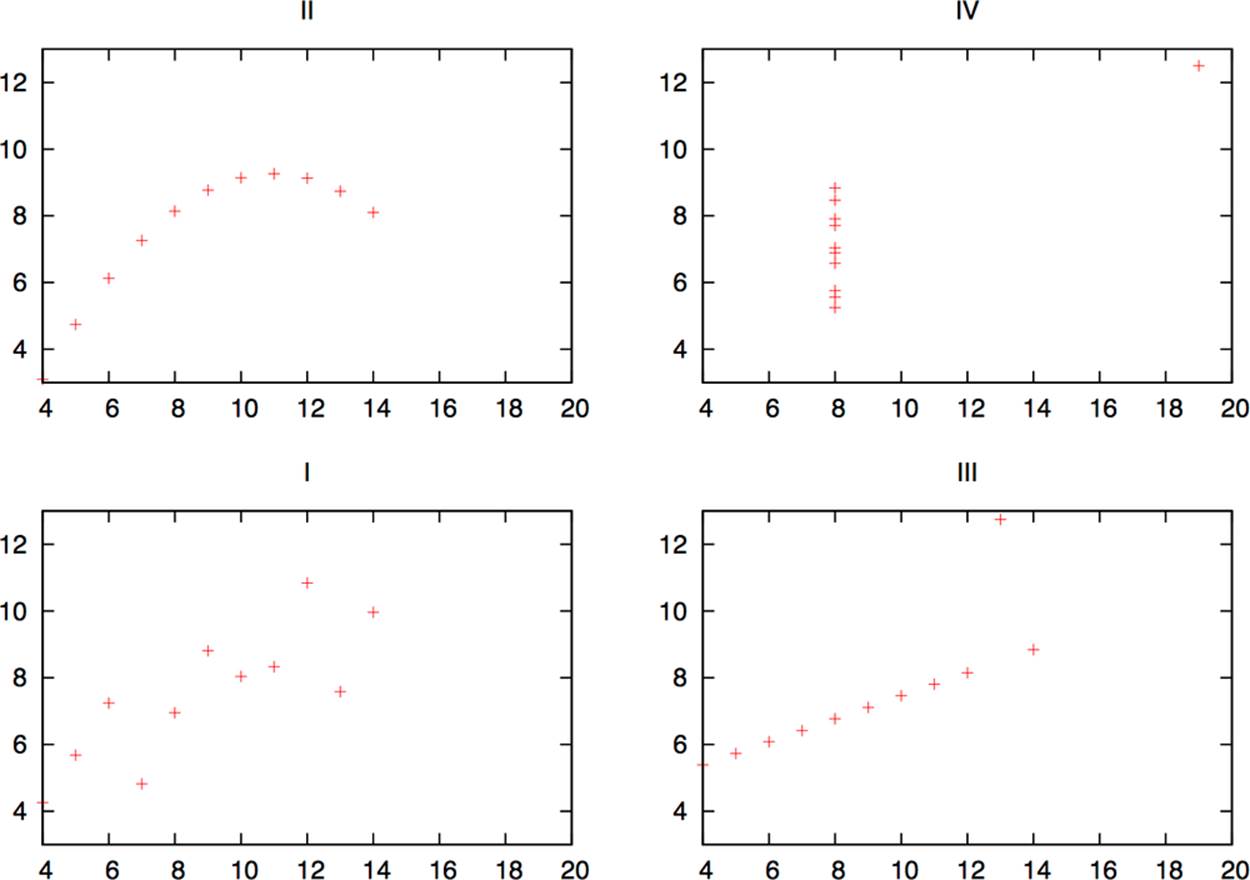
Figure 10-1. The Anscombe Quartet, visualized

As this example shows, simple visualization will identify significant features of the dataset that aren’t identified by reaching for the stats. The classic mistake in statistical analysis involves pulling out the math before looking at the data. For example, analysts will often calculate the mean and standard deviation of a dataset in order to produce a threshold value (normally around 3.5 standard deviations from the mean). This threshold is based on the assumption that the dataset is normally distributed; if it isn’t (and it rarely is), then simple counting will produce more effective results.

The Goal of EDA: Applying Analysis

The point of any EDA process is to move toward a model; that model might be a formal representation of the data, or it might be as simple as “raise an alarm when we see too much stuff” (where “too much” and “stuff” are, of course, exquisitely quantified). For information security, we will discuss four basic goals for data analysis: alarm construction, forensics, defense construction, and situational awareness.

When used as an alarm, an analytic process involves generating some kind of number, comparing it against a model of normal activity, and determining if the observed activity requires an analyst’s attention. An anomaly isn’t necessarily an attack, and an attack doesn’t necessarily merit a response. A good alarm will be based on phenomena that are predictable under normal circumstances, which the defender can do something about, and which the attacker must disrupt to reach his goals.

The problem in operational informational security isn’t creating alarms—it’s making them manageable. The first thing an analyst has to do when she receives an alarm is provide context—validating that the threat is real, ensuring that it’s relevant, determining the extent of the damage, and recommending actions to take place. False positives are a signficant problem, but they do not represent the whole scope of failure modes for alarms. Good analysis can increase the efficacy of alarms. See Chapter 7 for a more extensive discussion of this.

The majority of security analysis is forensic analysis, taking place after an event has occurred. Forensic analysis may begin in response to information from anywhere: alarms, IDS signals, user reports, or newspaper articles.^[17^]

A forensic analysis begins with some datum, such as an infected IP address or a hostile website. From there, the investigator has to find out as much as possible about the attack—the extent of the damage, other activities by the attacker, a timeline of the attack’s major events. Forensic analysis is often the most data-intensive work an analyst can do, as it involves correlating data from multiple sources ranging from traffic logs to personnel interviews and looking through archives for data stored years ago.

Alarms and forensic analysis are both reactive measures, but an analyst can also use data proactively and construct defenses. As analysts, we have a set of tools, such as policy recommendations, firewall rules, and authentication, that can be used to implement defenses. The challenge when doing so is that these measures are fundamentally restrictive; from a user’s perspective, security is a set of rules that limit their behavior now in order to prevent some abstract bad thing from happening later.

People are always the last line of defense in information security. If security is implemented poorly or arbitarily, it encourages an adversarial relationship between system administrators and users, and before long, everything is moving on port 80. Analysis can be used to determine reasonable constraints that will limit attackers without imposing an undue burden on users.

Alarms, forensics, and redesign are all focused on the attack cycle—detecting attacks, understanding attacks, and recovering from attacks. Throughout this cycle, however, there is a constant dependence on knowledge management. Knowledge management in the form of inventories, past history, lookup data, and even phone books changes processes from rolling disasters into manageable disasters.

Knowledge management affects everything. For example, almost all intrusion detection systems (especially signature management systems) focus on packet contents without knowing, for example, that the IIS exploit they’ve helpfully identified was aimed at an Amiga 3000 running Apache.^[18^] In IDSes, a false positive is usually a sign that the IDS copped out early. Maintaining inventory and mapping information is a necessary first step toward developing effective alarms; many attacks are failures, and that failure can be identified through context and the alert trashed before it annoys analysts.

Good inventory and past history data can also be used to speed a forensic investigation. Many forensic analyses are cross-referencing different data sources in order to provide context, and this information is predictable. For example, if I have an internal IP address, I’ll want to know who owns it and what software it’s running.

Knowledge management requires pulling data from a number of discrete sources and putting it in one place. Information like ASNs, whois data, and even simple phone numbers are often stored in dozens if not hundreds of variably maintained databases and subject to local restrictions and politics. Internal network status is often just as chaotic, if not more so because almost invariably people are running services on the network that nobody knows about. Often, the very process of identifying assets for an ops floor will help network management and IT concerns in general.

As you look at data, keep in mind the goals of the data analysis. In the end, you have to figure out what the process is for—whether it’s an alarm, timeline reconstruction, or figuring out whether you can introduce a firewall rule without dealing with pitchforks and torches.

EDA Workflow

Figure 10-2 is a workflow diagram for EDA in infosec. As this workflow shows, the core EDA process is a loop involving EDA techniques, extracting phenomena and analyzing them in more depth. EDA begins with a question, which can be as open-ended as “What does typical activity look like?” The question drives the process of data selection. For example, addressing a question such as “Can BitTorrent traffic be identified by packet size?” could involve selecting traffic communicated with known BitTorrent trackers or traffic that communicated on ports 6881–6889 (the common BitTorrent ports).

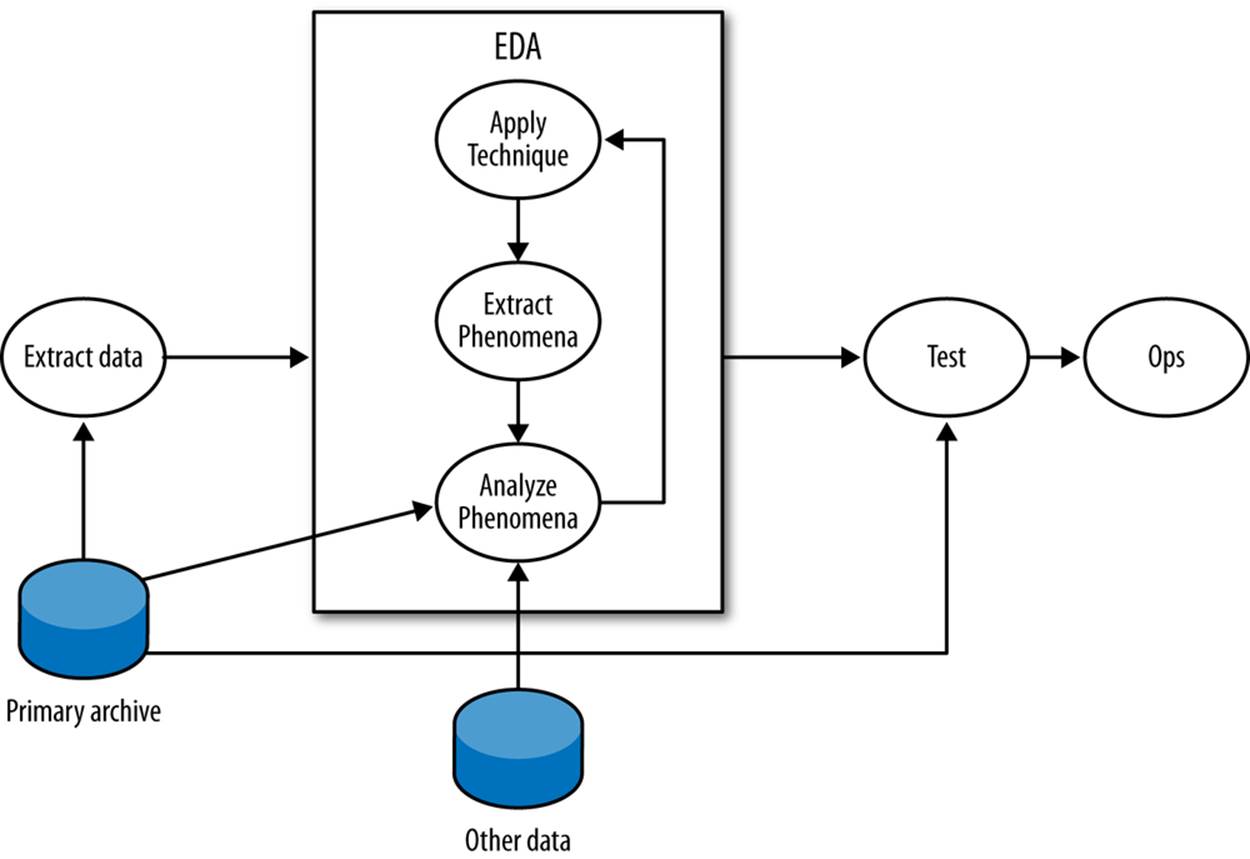
Figure 10-2. A workflow for exploratory data analysis

In the EDA loop, an analyst repeats three steps: summarizing and examining the data using a technique, identifying phenomena in the data, and then examining those phenomena in more depth. An EDA technique is a process for taking a dataset and summarizing it in some way that allows aperson to identify phenomena worth investigating. Many EDA techniques are visualizations, and the majority of this chapter is focused on visual tools. Other EDA techniques include data-mining approaches such as clustering, and classic statistical techniques such as regression analysis.

EDA techniques provide behavioral cues that can then be used to go back to the original data, extract particular phenomena from that dataset and examine them in more depth. For example, looking at port 6881–6889 traffic, an analyst finds that hosts often have flows containing between 50 and 200 bytes of payload. Using that information, he goes back to the original data and uses Wireshark to find out that those packets are BitTorrent control packets.

This technique-extract-analyze process can be repeated indefinitely; finding phenomena and knowing when to stop are arts learned through experience. Analysis involves an enormous number of false positives because the most effective initial formulations are broad and prone to false positives. The EDA process will often require looking at multiple data sources. For example, an analyst looking at BitTorrent data could consult the protocol definition or run a BitTorrent client himself to determine whether the properties observed in the data hold true.

At some point, the EDA process has to stop. On the completion of EDA, an analyst will usually have multiple potential mechanisms for answering the initial question. For example, when looking for periodic phenomena such as dial-homes to botnet C&Cs, it’s possible to use autocorrelation, Fourier analysis, or simply count time in bins. Once an analyst has options, the real question is which one to use, which is determined by a process usually driven by testing and operational demand.

The testing process should take the techniques developed during EDA and determine which ones are most suitable for operational use. This phase of the process involves constructing alarms and reports. See Chapter 7 on anomaly detection for more information about the criteria that make a good alarm.

Variables and Visualization

The most accessible and commonly approached EDA techniques are visualizations. Visualizations are tools, and based on the type of data examined and the goal of the analysis, there are a number of specific visualizations that can be applied to the task. In order to understand data, we have to start by understanding variables.

A variable is a characteristic of an entity that can be measured or counted, such as weight or temperature. Variables can change between entities or over time; the height of a person changes as she ages, and different people have different heights.

There are four categories of variables, which readers who have had an elementary statistics course will be familiar with. I’ll review them briefly here, in descending order of rigor:

Interval

An interval variable is one where the difference between two values is meaningful, but the ratio between two values has no meaning. In network traffic data, the start time of an event is the most common form of interval data. For example, an event may be recorded at 100 seconds after midnight, and another one at 200 seconds after midnight. The second event takes place after the first one, but it isn’t meaningful to talk about it taking place “twice as long” after the first one since there’s no real concept of “zero start time.”

Ratio

A ratio variable is like an interval variable, but also has a meaningful form of “zero,” which enables us to discuss ratio variables in terms of multiplication and division. One form of a ratio variable is the number of bytes in a packet. For example, we can have a packet with 200 bytes, and another one with 400 bytes. As with interval variables, we can describe one as larger than the other, and we can also describe the second packet as “twice as large” as the second one.

Ordinal

Data is in numerical order, but does not have fixed intervals. Customer ratings fall in this category. A rating of 5 is higher than 4, and 4 is higher than 3, so you can be assured that 5 is also higher than 3. But you can’t say that the degree of customer satisfaction goes up the same from 3 to 4 and from 4 to 5. (A common error is to base calculations on this, treating ratings as interval or ratio data.)

Nominal

This data is just named rather than numeric, as the term “nominal” indicates. There is no order to it. Data of this type that you commonly track include your hosts and your services (web, email, etc.).

Data isn’t necessarily ordinal just because it’s designated by numbers. Your ports are nominal data. Port 80 is not “higher” in some way than port 25; it’s best just to think of the numbers as alternative names for your HTTP port, your SMTP port, etc.

Interval, ratio, and ordinal variables are also referred to as quantitative, while nominal variables are also called qualitative. Interval and ratio variables can be further divided into discrete and continuous variables. A discrete variable has an indivisible difference between every value, while continuous variables have infinitely divisible differences. In network traffic data, almost all data collected is discrete. For example, a packet can contain 9 or 10 bytes of payload, but nothing in between. Even values such as start time are discrete, even if the subdivisions are extremely fine. Continuous variables are generally derived in some way, such as the average number of bytes per packet.

Univariate Visualization: Histograms, QQ Plots, Boxplots, and Rank Plots

Based on the type of variable measured, we can choose different visualizations. The most basic visualizations are applied to univariate data, which consists of one observed variable per unit measured. Examples of univariate measurements include the number of bytes per packet or the number of IP addresses observed over a period.

Histograms

A histogram is the fundamental plot for ratio and interval data; it is a count of how often a variable takes each possible value. A histogram consists of a set of bins, which are discrete ranges of values, and frequencies. Thus, if you can receive packets at any rate from 0 to 10,000 a second, you can create 10 bins for the ranges 0 to 999, 1,000 to 1,999, and so on. A frequency is the number of times that the observed value occurred within the range of the bin.

GENERATING A HISTOGRAM

The base material for a histogram is a set of quantitative observations. At the R prompt, for example, a quick and dirty histogram can be generated from raw data.

> sample <- rnorm(10,25,5)

> sample

[1] 30.79303 25.52480 22.29529 29.20203 21.88355 19.73429 24.99312

[8] 20.79997 22.24344 24.29335

> hist(sample)

The rnorm function in R takes the sample size, the mean of the values, and their standard deviation as parameters and generates a set of random observations. As is normal with R, the hist function holds your hand a lot, automatically assigning bin widths, for example.

Handy arguments to remember with the hist function include:

prob (takes a Boolean)

When set to True, the histogram will be plotted to have an area of 1. When set to False, the histogram will plot the frequencies.

breaks (takes multiple options)

breaks defines how the histogram bins up data. If set to a numeric value, it specifies the number of bins. If set to a vector, it uses the values of the vector as the breakpoints. It can also be set to a string to specify a predefined algorithm, or to a function pointer.

A histogram is valuable for data analysis because it helps you find structure in a variable’s distribution, and structure provides material for further investigation. In the case of the histogram, that structure is generally a mode, the most commonly occuring value in a distribution. In a histogram, modes appear as peaks. Histogram analysis almost invariably consists of two questions:

1. Is the distribution normal or another one I know how to use?

2. What are the modes?

As an example of this type of analysis, take a look at the histogram in Figure 10-3. This is a histogram of flow size distributions for BitTorrent sessions, showing a distinctive peak between about 78–82 bytes. This peak is defined by the BitTorrent protocol: it’s the result of a BitTorrent peer asking another peer if it has a particular piece of a file, and getting back “no” as an answer.

Modes enable you to ask new questions. Once you’ve identified modes in a distribution, you can go back to the source data and examine the records that produced the mode. In the example in Figure 10-3, you could go back to the times in the second mode (the 250–255 peak) and see whether the traffic showed any distinctive characteristics—short flows, long flows, communications with empty addresses, and so on. Modes direct your questions.

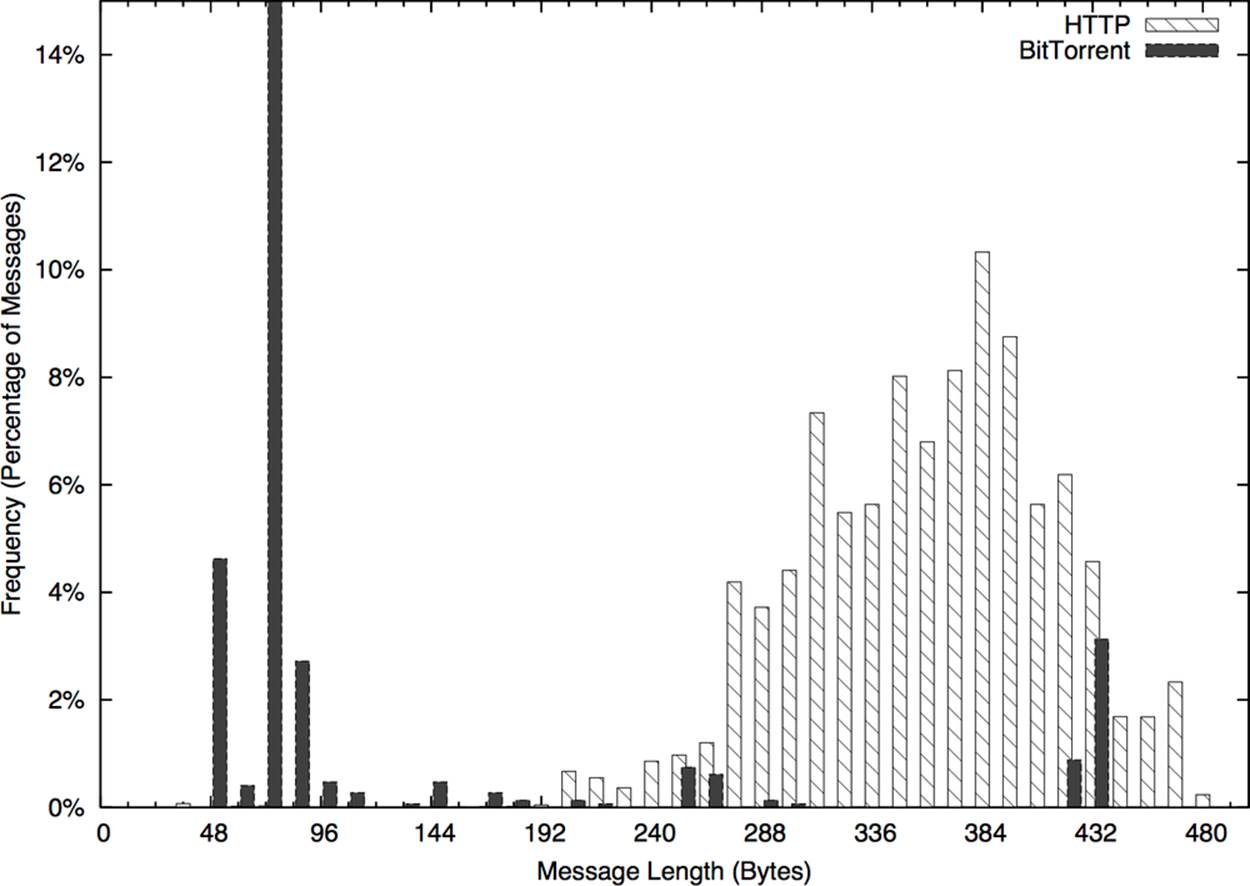
Figure 10-3. A distribution of BitTorrent flow sizes

This process of visualizing, then returning to the repository and pulling more detailed data is a good example of the iterative analysis shown in Figure 10-2. EDA is a cyclic process where analysts will return to the source (or multiple sources) repeatedly to understand why something is distinctive.

Bar Plots (Not Pie Charts)

A bar plot is the analog to a histogram when working with univariate qualitative data. Like a histogram, it plots the frequency of values observed in the dataset by using the height of various bars. Figure 10-4 is an example of such a plot, in this case showing the count of various services from network traffic data.

The difference between bar plots and histograms lies in the binning. Qualitative data can be grouped into ranges, and in histograms, the bins represent those ranges. These bins are approximations, and the range of values they contain can be changed in order to provide a more descriptive image. In the case of bar plots, the different potential values of the data are discrete, enumerable, and often have no ordering. This lack of ordering is a particular issue when working with multiple bar plots—when doing so, make sure to keep the same order in each plot and to include zero values.

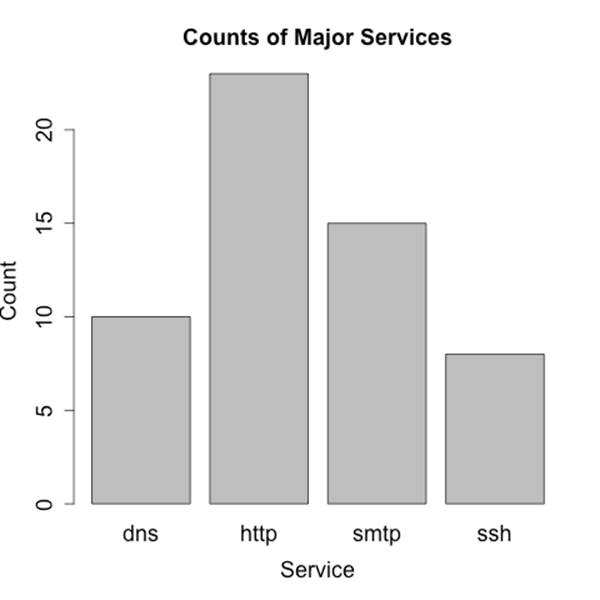
Figure 10-4. A bar plot showing the distribution of major services

In scientific visualization, bar plots are preferred over pie charts. Viewers have a hard time differentiating fine variations in pie slice sizes, variations that are much more apparent in bar plots.

The Quantile-Quantile (QQ) Plot

A Quantile-Quantile (QQ) plot compares the distributions of two variables against each other. A QQ plot is a two-dimensional plot, with the x-axis being the values of one distribution normalized as quantiles, and the y-axis being values of the second distribution again normalized as quantiles. For example, if I break each distribution into 100 centiles, the first point is the first percentile for each, the 50th point is the 50th percentile for each, and so on.

Figure 10-5 and Figure 10-6 show two QQ plots with the companion code following. These plots, generated using R’s qqnorm function, plot each distribution against a normal distribution. The first plot, a normal distribution, shows the expected behavior when two similar distributions are plotted on a QQ plot—the values track the diagonal. There is some deviation but it isn’t very severe. Compare the results with the uniform distribution in the second figure; in this one, significant deviations happen on the ends of the plot.

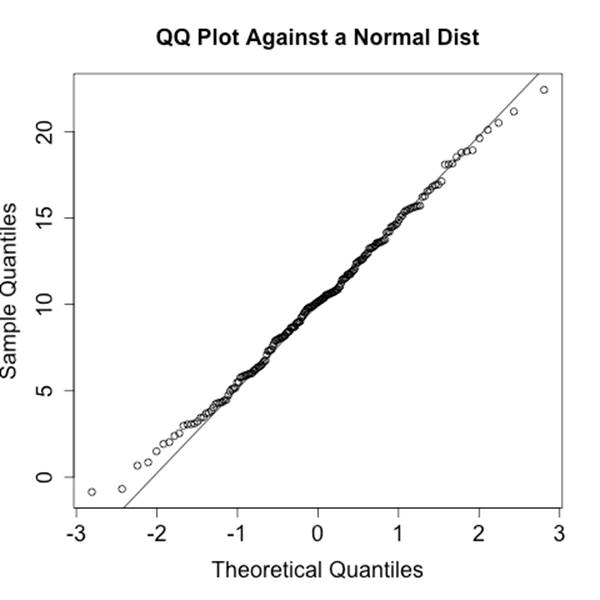
Figure 10-5. Example QQ plot against a normal distribution

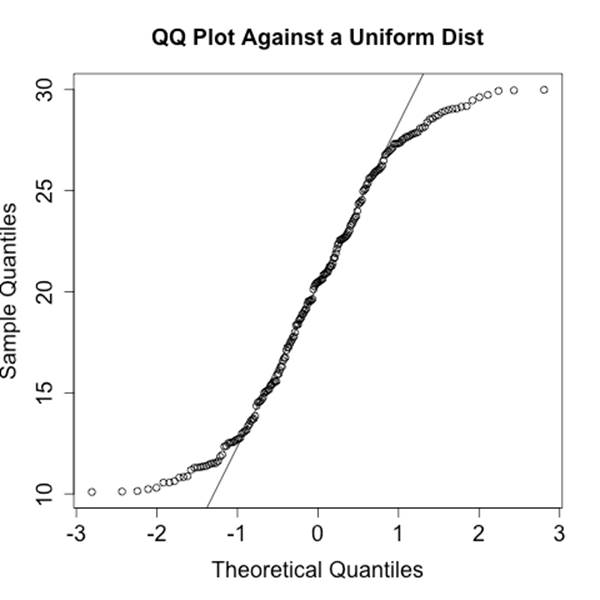
Figure 10-6. Example QQ plot against a uniform distribution

> # Generate a uniform and a normal distribution

> set.normal <- rnorm(n = 200, mean=10, sd = 5)

> set.unif <- runif(n = 200, min = 10, max = 30)

> # Plot against the norm for the normal set

> qqnorm(set.normal,main='QQ Plot Against a Normal Dist')

> qqline(set.normal)

> # Same drill for the uniform distribution

> qqnorm(set.unif, main='QQ Plot Against a Uniform Dist')

> qqline(set.unif)

R has a number of QQ plotting routines. The most important are qqnorm, which plots a dataset against the normal distribution; qqplot, which generates a qq plot comparing any two datasets; and qqline, which draws the reference line.

IS IT NORMAL?

In Chapter 6 and this chapter, we’ve discussed a number of techniques for determining whether or not a dataset is normally distributed, or to be more precise, can be satisfactorily modeled using a normal distribution. Parametric distributions, if applicable, open up a number of tools to us. The problem is that in raw network data they’re rarer than Yeti. Among the techniques listed are:

§ The Shapiro-Wilk Test (Example 6-4), a statistical normality test.

§ The Kolmogorov-Smirnov Test (Example 6-5), a general goodness-of-fit test.

§ Histograms (Histograms), visualizing the distribution.

§ QQ plots (Bar Plots (Not Pie Charts)), comparing the data against a normal.

Of all the tools available, I view visualization approaches (histograms and QQ plots) as the preferable option. My interest in acquiring a distribution is utilitarian. I’m looking for reasonable thresholds and something that matches the math well enough that I can use other tools because we don’t have the control to make very sensitive measurements. Attackers will usually be fairly easy to identify once you’ve picked the right metric. The classic mistake with using means and standard distributions without looking at the data is that most network security datasets have a number of outliers. These outliers end up producing ridiculously large standard deviations, and the resulting threshold is triggered only for egregious events.

The Five-Number Summary and the Boxplot

The five-number summary is a standard statistical shorthand for describing a dataset. It consists of the following five values:

§ The minimum value in a dataset

§ The first quartile of the dataset

§ The second quartile or median of the dataset

§ The third quartile of the dataset

§ The maximum value in the dataset

Quartiles are points that split the dataset into quarters, so the five numbers translate into the smallest value, the 25% threshold, the median, the 75% threshold, and the maximum. The five-number summary is a shorthand, and if you’re looking at a lot of datasets very quickly, it can provide you with a quick feel for what the set looks like.

The five-number summary can be visualized using a boxplot (Figure 10-7), which is also called a box-and-whiskers plot. A boxplot consists of five lines, one for each value in the five-number summary. The center three lines are then connected as a box (the box of the plot) and the outer two lines are connected by perpendicular lines (the whiskers) of the plot.

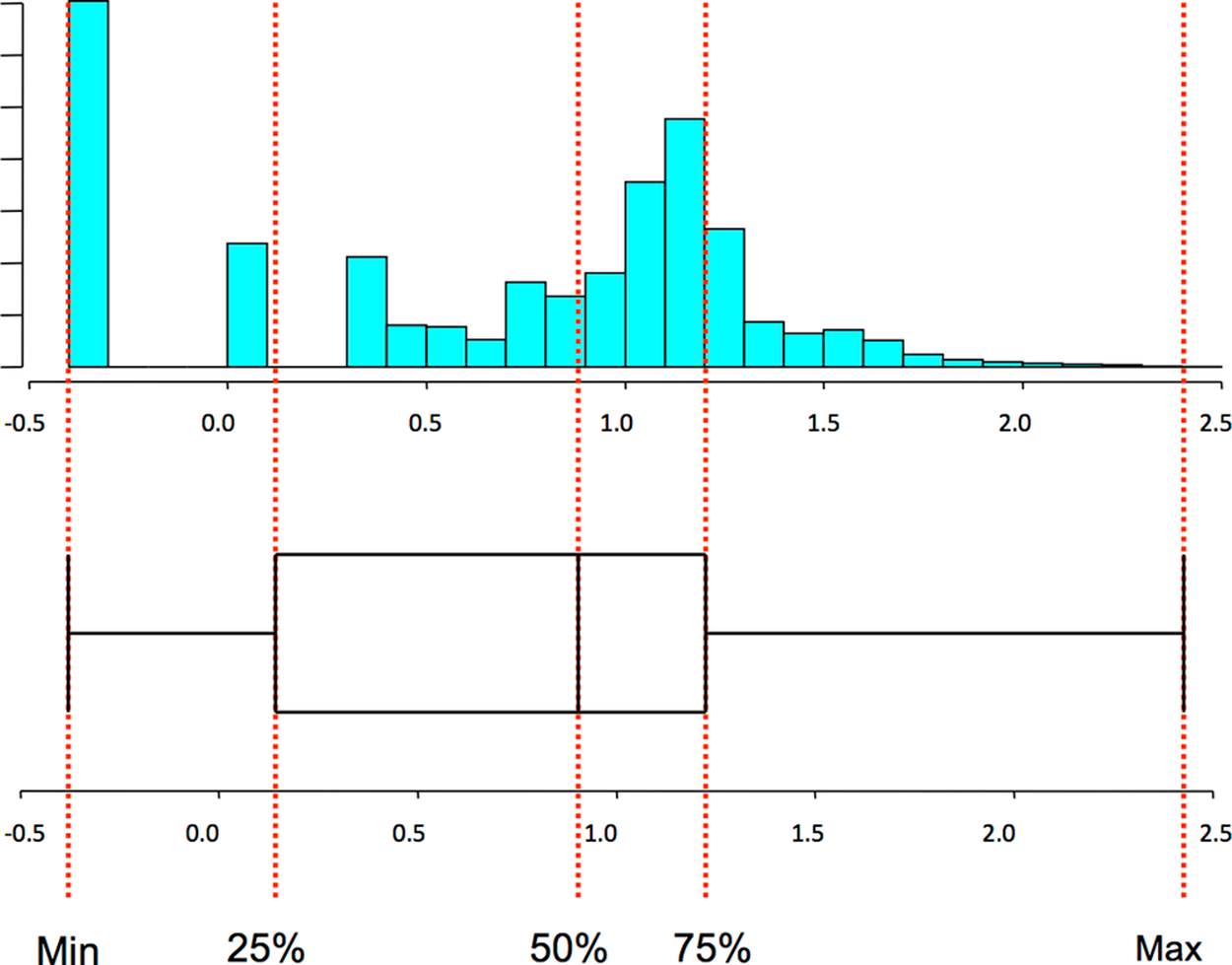
Figure 10-7. A boxplot and the corresponding histogram

Generating a Boxplot

In R, five-number summaries are generated using the fivenum command, as shown in the following example.

> s<-rnorm(100,mean=25,sd=5)

> fivenum(s)

[1] 14.61463 22.26498 24.50200 27.43826 37.99568

A basic boxplot is generated with the boxplot command, as follows, resulting in the image in Figure 10-8.

>boxplot(s)

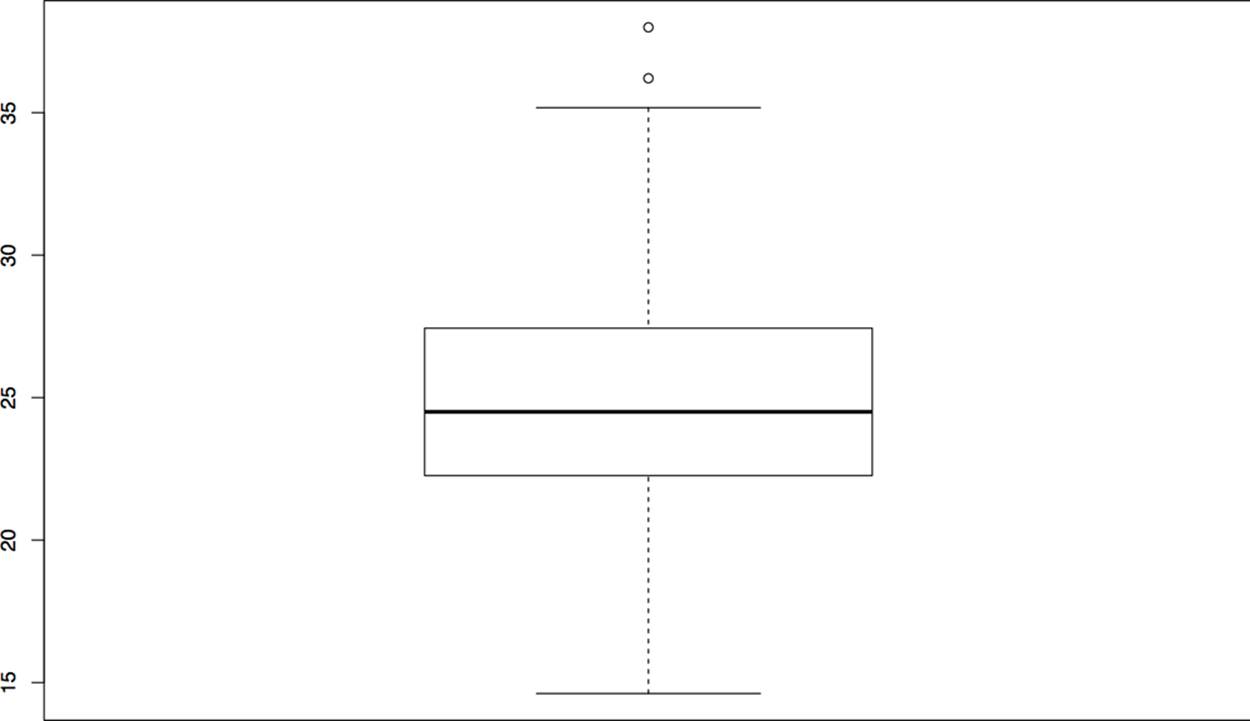
Figure 10-8. An example boxplot

Note that this plot produced a series of dots outside the whiskers. These are outliers, meaning they are far outside the first and third quartiles. By default, a low value is considered an outlier if its distance to the first quartile is more than 1.5 times the interquartile range (the difference between the first and third quartiles). Similarly, a high value is considered an outlier if its distance to the third quartile is more than 1.5 times the interquartile range.

Handy parameters to remember with boxplot include:

notch (Boolean)

Set to True, it places a notch at the median value of the boxplot. If two plots notches don’t overlap, it’s a strong indicator that their medians differ.

range (numeric)

Describes how far the whiskers will extend. The default value is 1.5, as described earlier in the sidebar. If you set range to zero, whiskers will extend as far as they need to and no values will be outliers.

When dealing with five-number summaries, it’s not unusual to toss in the mean (Figure 10-9). Consequently, you will often see boxplots that include the mean with an extra character, usually an x. In R, you have to do multiple plots on the same canvas to produce this, as follows:

>boxplot(s)

>points(mean(s), pch='x')

In this example, the pch parameter sets the character of the point; in this case, an x.

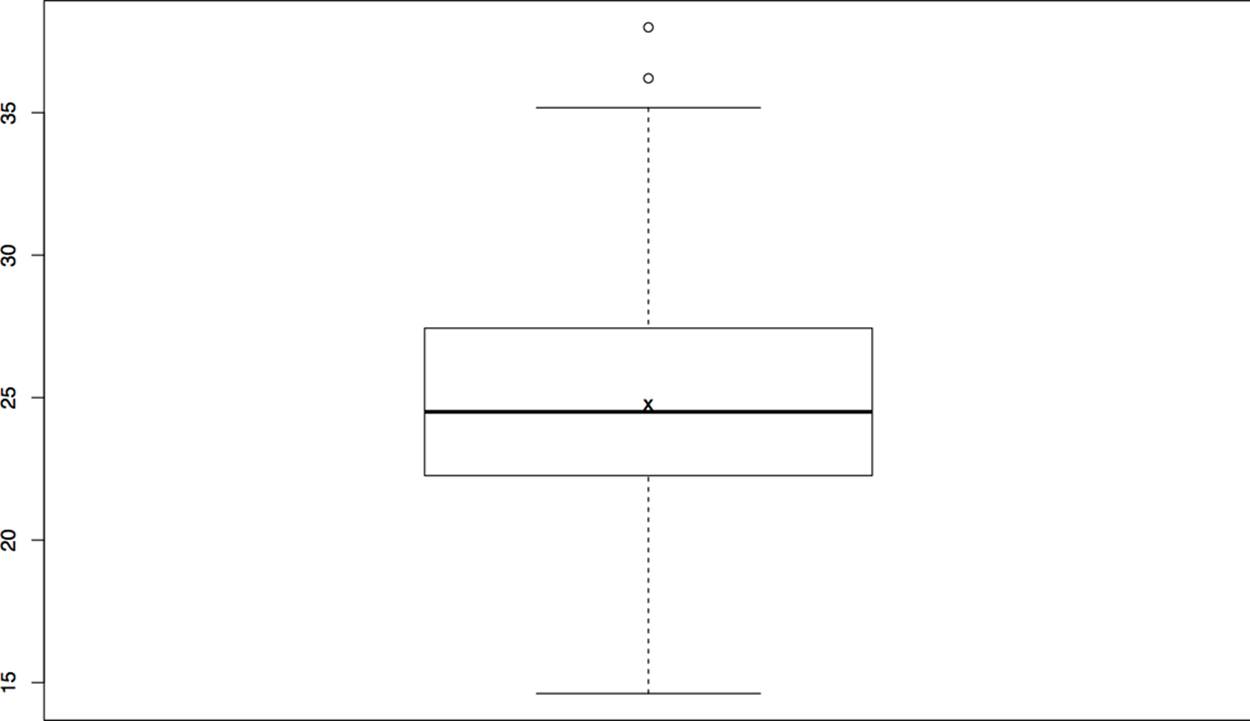
Figure 10-9. A boxplot with a mean

boxplot can take multiple vectors, making it a quick tool for comparing multiple discrete datasets. If, for example, you’ve identified several different phenomena in a dataset, you could split each one into a separate column for comparison. The following example shows this with some cooked scan data, producing the side-by-side boxplot in Figure 10-10.

> nonscan<-rnorm(100,mean=150,sd=30)

> scan<-runif(50,min=254,max=255)

> boxplot(nonscan,scan,names=c('nonscan','scan'))

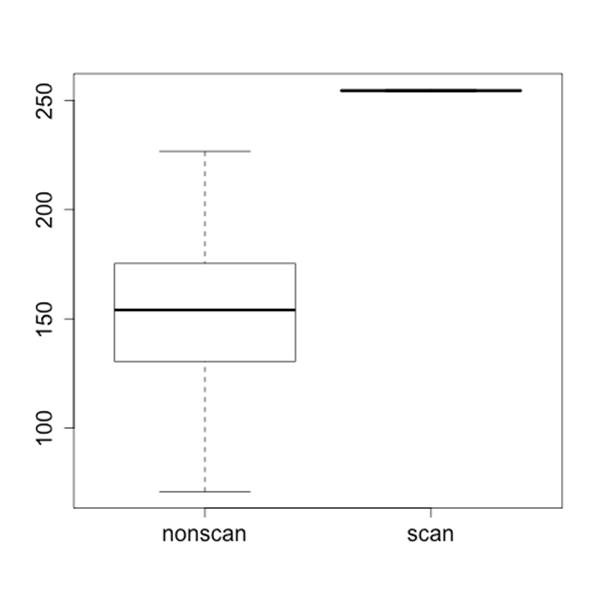
Figure 10-10. Side-by-side boxplots

I rarely find boxplots to be useful on their own. If I’m dealing with a single value, I’m going to get more information out of a histogram. Boxplots become more valuable when you start stacking bunches of them together, a situation where histograms are going to be just too busy to be meaningfully examined.

Bivariate Description

Bivariate data consists of two observed variables per unit measured. Examples of bivariate data include the number of bytes and packets observed in a traffic flow (which is an example of two quantitative variables), and the number of packets per protocol (an example of a quantitative and qualitative variable). The most common plots used for bivariate data are scatterplots (for comparing two quantitative variables), multiple boxplots (for comparing quantitative and qualitative variables), and contingency tables (for comparing two qualitative variables).

Scatterplots

Scatterplots are the workhorse of quantitative plots, and show the relationship between two ordinal, interval, or ratio variables. The primary challenge when analyzing scatterplots is to identify structure among the noise. Common features in a scatterplot are clusters, gaps, linear relationships, and outliers.

Let’s start exploring scatterplots by looking at completely unrelated data. Figure 10-11 is an example of a noisy scatterplot, generated in this case by plotting two uniform distributions against each other. This is a boring plot.

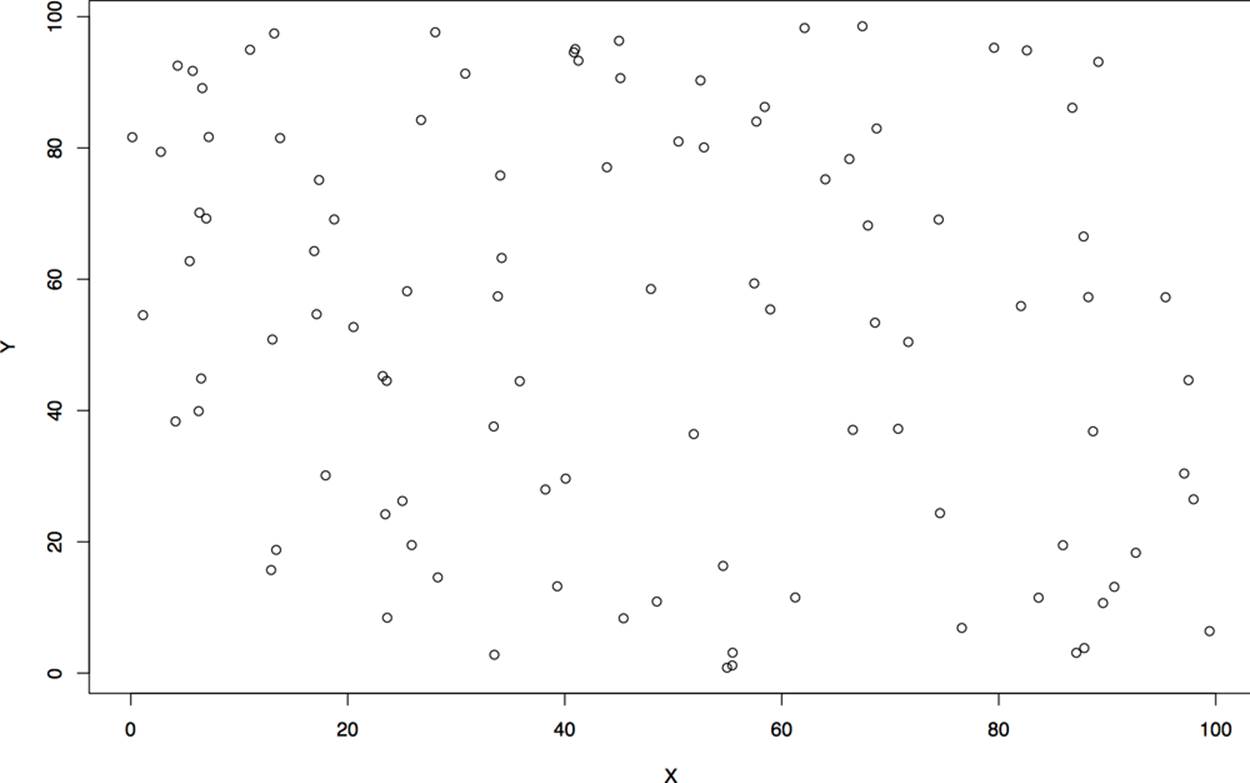
Figure 10-11. A boring scatterplot

Clusters and gaps are changes in the density of a scatterplot. The boring scatterplot in Figure 10-11 is a plot of uniform variables of unrelated density. If the two variables are related, then there should be a change in the density of the data somewhere on the plot. Figure 10-12 shows an example of clusters and gaps. In this example, there is a marked increase in activity in the lower-left quadrant, and a marked decrease in the upper-right quadrant.

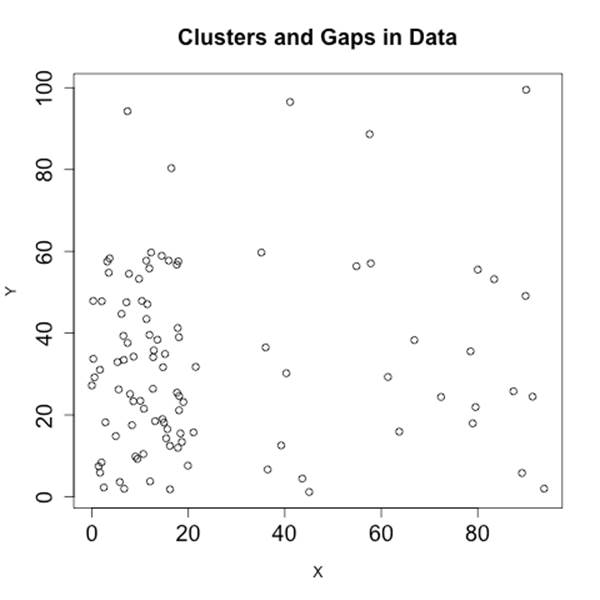
Figure 10-12. Clusters and gaps in data

Linear relationships, as the name indicates, appear in scatterplots as a line. The strength of the relationship can be estimated from the density of the points around the line. Figure 10-13 shows an example of three simple linear relationships of the form y=kx, but each relationship is progressively weaker and noisier.

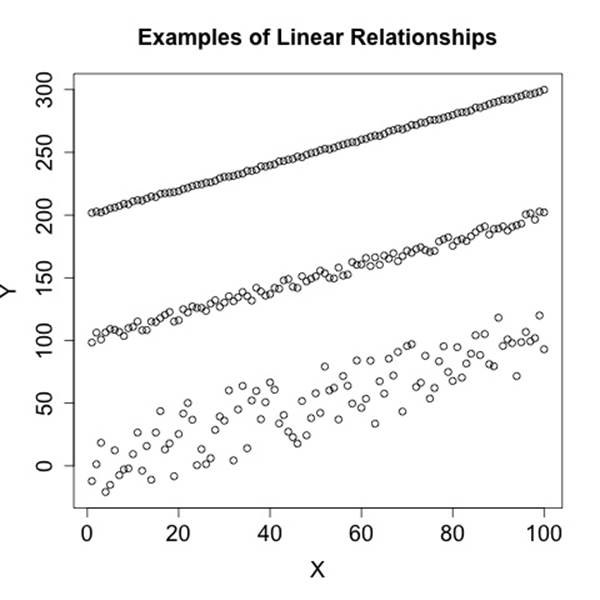
Figure 10-13. Linear relationships in data

Contingency Tables

Contingency tables are the preferred visualization when comparing categorical data against categorical data. A contingency table is simply a matrix: the rows list all the values one variable can have, the columns list all the values the other variable can have, and the entry in each cell is the number of observations that had both categories in common. Depending on the implementation, contingency tables also include a row and column containing the marginals for that row, a sum of all the values occurring in the row.

In R, contingency tables are constructed using the table command, which returns a table that can then be queried for marginals, as shown here:

# An example R table, created from two vectors of hosts and services

> hosts[0:3]

[1] "A" "B" "A"

> services[0:3]

[1] "http" "dns" "smtp"

> # Table creation, hosts, and services have to be the same length

> info.table<-table(hosts,services)

> info.table

services

hosts dns http smtp ssh

A 2 15 10 0

B 6 5 3 4

C 3 3 1 2

> # You can access the marginals by calling margin.table

> margin.table(info.table)

[1] 54

> margin.table(info.table, 1)

hosts

A B C

27 18 9

> margin.table(info.table, 2)

services

dns http smtp ssh

11 23 14 6

Multivariate Visualization

A multivariate dataset is one that contains at least three variables per unit measured. Multivariate visualization is more of a technique rather than a specific set of plots. Most multivariate visualizations are built by taking a bivariate visualization and finding a way to add additional information. The most common approaches include colors or changing icons, plotting multiple images, and using animation.

Building good multivariate visualizations requires providing information from each of the datsets without drowning the reader in details. It’s easy to plot a dozen different datasets on the same chart, but the results are often confusing.

The most basic approach for multivariate visualization is to overlay multiple datasets on the same chart, using different tickmarks or colors to indicate the originating dataset. As a rule of thumb, you can plot about four series on a chart without confusing a reader. When picking the colors or symbols to use, keep the following in mind:

§ Don’t use yellow; it looks too much like white and is often invisible on printouts and monitors.

§ Choose symbols that are very different from each other. I personally like the open circle, closed circle, triangle, and cross.

§ Choose colors that are far away from each other on the color wheel: red, green, blue, and black are my preferred choices.

§ Avoid complex symbols. Many plotting packages offer a variety of asterisk-like figures that are hard to differentiate.

§ Be consistent with your color and symbol choices, and don’t overlap their domains. In other words, don’t decide that red is HTTP and triangles are FTP.

For more information on plotting multiple series in R, consult Annotating a Visualization.

An alternative to plotting multiple sets on the same chart is to use multiple small plots next to each other. Commonly called trellis plots, Figure 10-14 is a good example generated by R’s pairs command. When run on a data frame, pairs generates a matrix like the one shown in Figure 10-14—each pair of variables is a distinct scatterplot. Each scatterplot shows the relationship between the pair, and as this example shows it’s very easy to quickly identify that volume and articles seem to have some relationship while everything else looks unrelated.

R’s pairs plot is a powerful data exploration tool and is a good example of the expressive power of multiple visualizations. By relating multiple simple visualizations together in a well-defined and clear structure, you can process an enormous amount of data quickly. The key to building visualizations like this one is simplicity—small plots need to be careful with how they use real estate.

I find that trellis plots are usually the best option for plotting multivariate data because they provide a clean and user-controlled mechanism for showing the relationship between different variables. The minimal layout of Figure 10-14 is an important design feature to pay attention to in multivariate visualization. Trellis plots usually have an enormous amount of redundant metadata (e.g., axes, ticks, and labels) relative to the number of plots. To address this problem, use extremely minimal data representations in the plots: drop redundant axes, and remove internal labels and ticks.

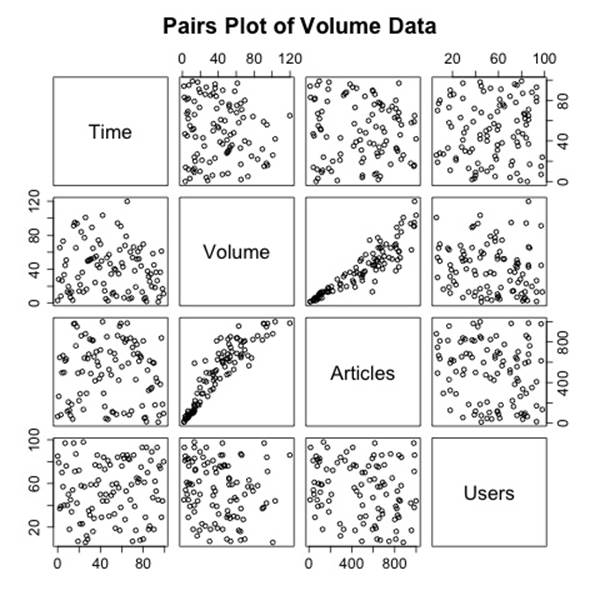
Figure 10-14. Trellis plot of volume data

Animation is pretty much what it says on the tin: you create multiple images and then step through them. In my experience, animation doesn’t work very well. It reduces the amount of information directly observable by an analyst, who has to correlate what’s going on in her memory as opposed to visually.

Operationalizing Security Visualization

EDA and visualization are part of the exploratory process and, as such, are somewhat rough around the edges. The EDA process involves a large number of dead ends and false starts. During the operationalization phase of an analytic process, the visualizations will need to be modified in order to supplement action and response. Additional processing and modification is needed to polish a visualization sufficiently for it to work on the floor. The following rules provide examples of good and bad visualizations and how to address the problems of visualizing data for information security.

Rule one: bound and partition your visualization to manage disruptions

When plotting security information, you need to expect and manage disruptions—after all, the whole point of looking for security events is to find disruptive activity. Plotting features like autoscaling can work against you by hiding data when something weird happens. For example, consider a count of anomalous events such as in Figure 10-15. This plot has two anomalies, but one is obscured by the need to plot the second.

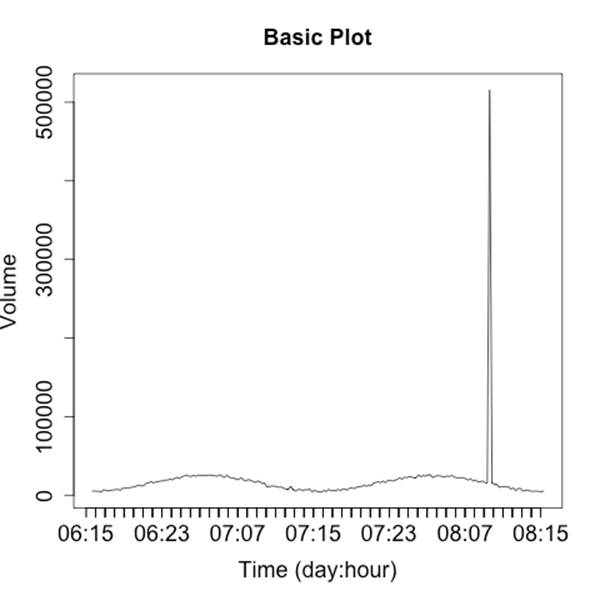
Figure 10-15. Autoscale’s impact on disruptive event visualization

There are two strategies for dealing with these spikes. The first is to use logarithmic scaling on the dependent (y) axis. Log scaling replaces the linear scale with a logarithmic scale. For example, the ticks on the axis go from being 10, 20, 30, 40 to 10, 100, 1000, 10000. Figure 10-16 shows a logarithmic plot of the same phenomenon. Using a logarithmic scale will reduce the difference between the major anomaly and the rest of the data.

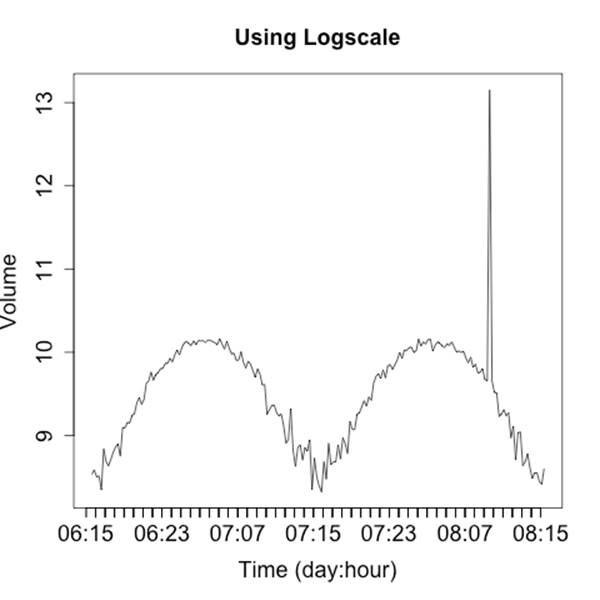
Figure 10-16. Using a log scale plot to limit the impact of large outliers

A logarithmic scale is suitable for EDA, and most tools provide an option to automatically plot data this way. With R, you pass in a log parameter to the plotting command to indicate which axis should be logarithmic (e.g., log="y").

I don’t like using logarithmic scales when developing an operational visualization, however. With logarithmic scales you tend to lose information about typical phenomena—the curve for typical traffic in Figure 10-16 is deformed by the logarithmic scale. Also, the explanation of what a logarithmic scale is a bit recondite; I don’t want to have to explain logarithmic scaling over and over again. When somebody is looking at the same data repeatedly, I’d prefer to keep it linear.

For these reasons, I prefer to keep the scaling on a plot consistent and identify and remove outliers. We’ve seen an example of this in Figure 10-8, where R automatically splits outliers from the boxplot. When developing an operational plot, I estimate the range of the plot, and usually set the upper limit displayed to the 98th percentile of the observed data. Then, when an anomaly occurs, I plot it separately and differently from the other data to indicate that it is an anomaly. Figure 10-17 shows a simple example of this.

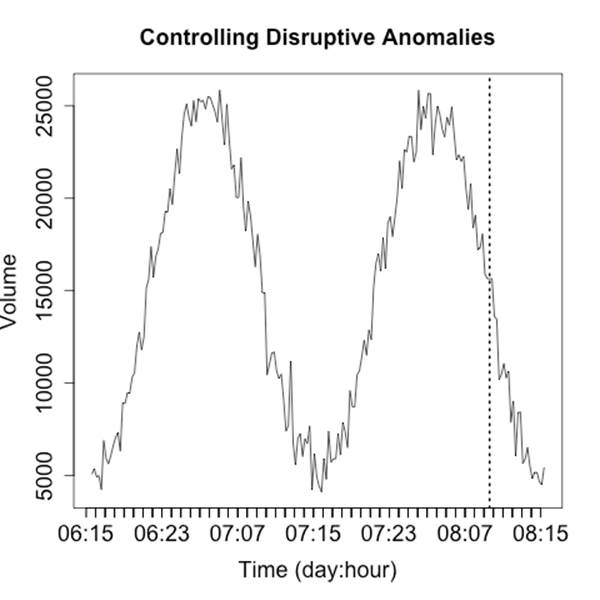
Figure 10-17. Partitioning anomalies out from normal data

The anomaly in Figure 10-17 is identified by the single line indicating that it’s off the scale. The second anomaly (at 07:11) is not detected by that process, but the event is now obvious through visualization. That said, the anomaly marker is completely meaningless without further information and training, which leads into rule two.

Rule two: label anomalies

If rule one is in place, then you’ve already established some basic rules for discerning anomalies from normal traffic. Operational visualization is an aid to anomaly detection, so the same rules as constructing IDS (see Chapter 7) apply—prefetch data to reduce the operator’s response time. As an example, the anomaly in Figure 10-18 is annotated with the information about what caused the anomaly as well as some statistics.

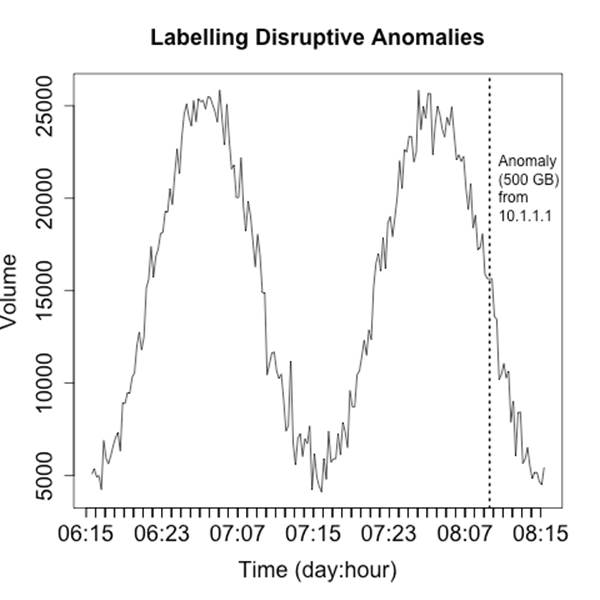
Figure 10-18. Labeling anomalies to aid investigation

Labeling anomalies on the plot can be useful for rapid reference, but if there are too many anomalies (and working off of rule one, you should expect that there will be too many anomalies). You can see this happening in Figure 10-18 where the label, while informative, is already consuming about a fifth of the horizontal space available. A better approach is to explain the anomalies in a separate table next to the visualization, which allows you to include as much data as necessary.

Rule three: use trendlines, distinguish artifacts from observations

Operational visualizations need to balance summarization and smoothing techniques that can help the analyst process data without getting mired in details, while at the same time providing the analyst with the actual data that happened and not thinking for him. As a result, when I operationally visualize data I prefer to include the raw data and then some kind of smoothing trendline at the same time. Figure 10-19 is a simple example of this kind of visualization, where a moving average is used to smooth out the observed disruptions.

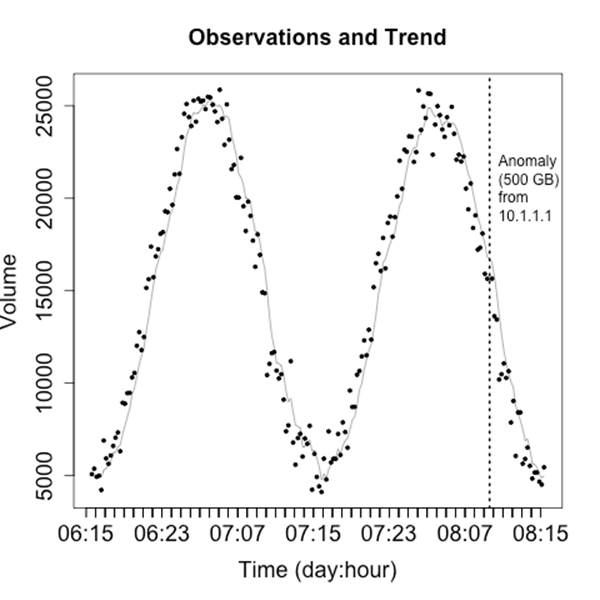
Figure 10-19. Moving average over direct observations

When creating visualizations like this, you need to ensure that the analyst can clearly differentiate between the data (the original) information and the artifacts you’ve created to aid analysis. You also need, as per rule one, to keep track of the impact of disruptive events—you don’t want them interfering with your smoothing.

Rule four: be consistent across plots

Visualization exploits our pattern matching capabilities. However, those capabilities just love to run rampant on the vaguest hint. For example, you decide to pick a red line to represent HTTP traffic in a per-host activity. If you then decide to use a red line to represent incoming traffic in the same suite of visualizations, somebody is going to assume it’s HTTP traffic again.

Rule five: annotate with contextual information

In addition to labeling anomalies, it’s good to include unobtrusive contextual data that can help facilitate analysis. The example shown in Figure 10-20 adds some gray bars to indicate whether or not activity is taking place during or outside business hours.

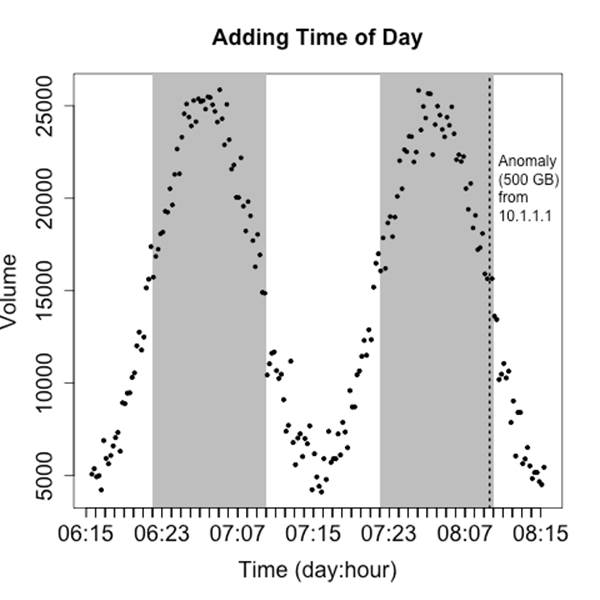
Figure 10-20. Adding some color to identify time of day

Rule six: avoid flash in favor of expressiveness

Finally, recognize that operational visualization is intended to be processed quickly and repeatedly. It’s not a showcase for innovative graphic representation. The goal of operational visualization should be to express information quickly and clearly. Graphically excessive features like animation, unusual color choices, and the like will increase the time it takes to process the image without contributing information.

Be particularly careful about visualizations based on real-world or cyberspace metaphors. Whimsy wears thin very quickly, and we’re not dealing with the physical world here. Metaphors such as “opening a desk” or “rattling all the doors in a building” (visualizations I’ve seen tried and the less said about them the better) often look neat in concept, but they usually require complex interstitial animations (which take up time) and lose information because of the metaphor. Focus on simple, expressive, serious displays.

Rule seven: when performing long jobs, give the user some status feedback

When I run SiLK queries, I have a habit of running them with the --print-file switch active, not because I care about which files are being accessed, but in order to have an indicator of whether the process is running or if the system is hung. When building visualizations, it’s important to know how long it will take to complete one and to provide the user with some feedback that the visualization is actually being generated.

Further Reading

1. Greg Conti, Security Data Visualization: Graphical Techniques for Network Analysis (No Starch Press, 2001).

2. NIST Handbook of Explorator Data Analysis

3. Cathy O’Neil and Rachel Schutt, Doing Data Science (O’Reilly, 2013).

4. Edward Tufte, The Visual Display of Quantitative Information (Graphics Press, 2001).

5. John Tukey, Exploratory Data Analysis (Pearson, 1997).