Essential MATLAB for Engineers and Scientists (2013)

PART 2 Applications

CHAPTER 14 Introduction to Numerical Methods

Abstract

A major scientific use of computers is in finding numerical solutions to mathematical problems which have no analytical solutions (i.e., solutions which may be written down in terms of polynomials and standard mathematical functions). In this chapter we look briefly at some areas where numerical methods have been highly developed, e.g., solving non-linear equations, evaluating integrals, and solving differential equations. The objectives of this chapter are to introduce numerical methods for solving equations, evaluating definite integrals, solving systems of ordinary differential equations and solving a parabolic partial differential equation.

Keywords

Linear and non-linear equations; Algebraic systems; Ordinary differential equations; Partial differential equations

CHAPTER OUTLINE

Equations

Newton's method

Complex roots

The Bisection method

fzero

roots

Integration

The Trapezoidal rule

Simpson's rule

quad

Numerical differentiation

diff

First-order differential equations

Euler's method

Example: bacteria growth

Alternative subscript notation

A predictor-corrector method

Linear ordinary differential equations (LODEs)

Runge-Kutta methods

A single differential equation

Systems of differential equations: chaos

Passing additional parameters to an ODE solver

A partial differential equation

Heat conduction

Complex variables and conformal mapping

Joukowski airfoil

Other numerical methods

Summary

Exercises

THE OBJECTIVES OF THIS CHAPTER ARE TO INTRODUCE NUMERICAL METHODS FOR:

■ Solving equations.

■ Evaluating definite integrals.

■ Solving systems of ordinary differential equations.

■ Solving a parabolic partial differential equation.

14.1. Equations

In this section we consider how to solve equations in one unknown numerically. The usual way of expressing the problem is to say that we want to solve the equation , i.e., we want to find its root (or roots). This process is also described as finding the zeros of . There is no general method for finding roots analytically for an arbitrary .

14.1.1. Newton's method

Newton's method is perhaps the easiest numerical method to implement for solving equations, and was introduced briefly in earlier chapters. It is an iterative method, meaning that it repeatedly attempts to improve an estimate of the root. If is an approximation to the root, we can relate it to the next approximation using the right-angle triangle in Figure 14.1:

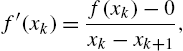
where is . Solving for gives

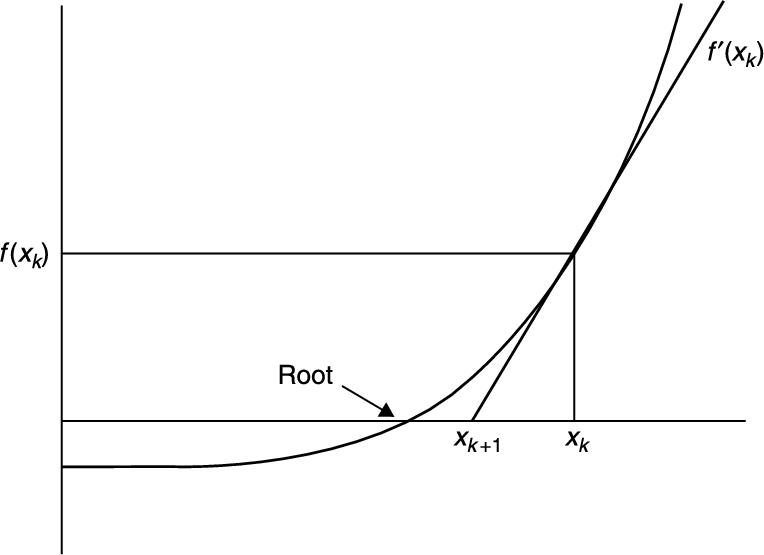
FIGURE 14.1 Newton's method.

A structure plan to implement Newton's method is:

1. Input starting value and required relative error e

2. While relative error repeat up to , say:

Print and

3. Stop.

It is necessary to limit step 2 since the process may not converge.

A script using Newton's method (without the subscript notation) to solve the equation is given in Chapter 7. If you run it you will see that the values of x converge rapidly to the root.

As an exercise, try running the script with different starting values of to see whether the algorithm always converges.

If you have a sense of history, use Newton's method to find a root of . This is the example used when the algorithm was first presented to the French Academy.

Also try finding a non-zero root of , using Newton's method. You might have some trouble with this one. If you do, you will have discovered the one serious problem with Newton's method: it converges to a root only if the starting guess is ‘close enough’. Since ‘close enough’ depends on the nature of and on the root, one can obviously get into difficulties here. The only remedy is some intelligent trial-and-error work on the initial guess—this is made considerably easier by sketching or plotting it with MATLAB (see Figure 14.2).

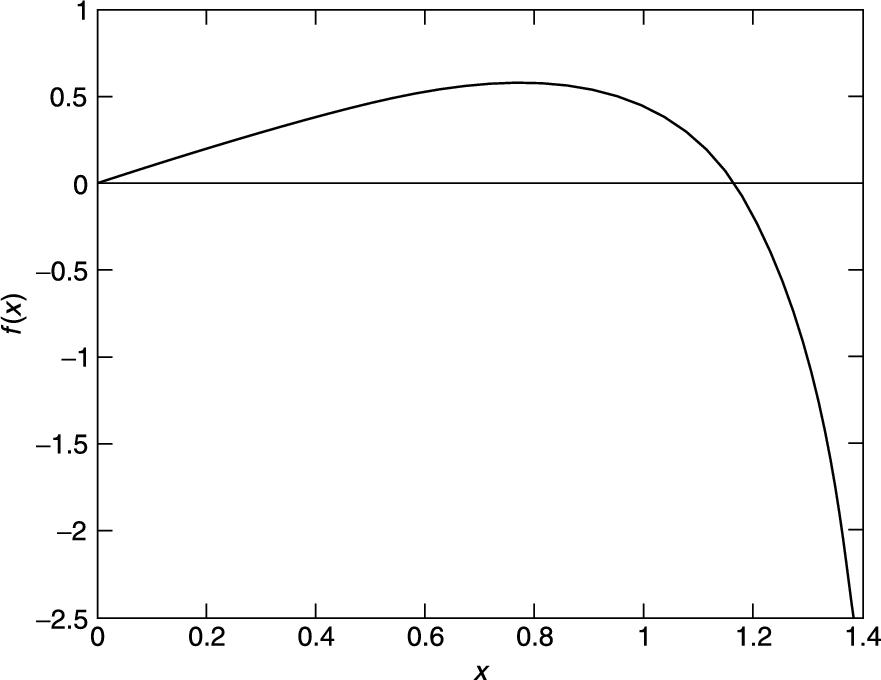
FIGURE 14.2 f(x) = 2x − tan(x).

If Newton's method fails to find a root, the Bisection method, discussed below, can be used.

14.1.1.1. Complex roots

Newton's method can also find complex roots, but only if the starting guess is complex. Use the script in Chapter 7 to find a complex root of . Start with a complex value of 1 + i say, for x. Using this starting value for x gives the following output (if you replace disp( [x f(x)] ) in the script with disp( x )):

0.0769 + 0.6154i

-0.5156 + 0.6320i

-0.4932 + 0.9090i

-0.4997 + 0.8670i

-0.5000 + 0.8660i

Zero found

Since complex roots occur in complex conjugate pairs, the other root is .

14.1.2. The Bisection method

Consider again the problem of solving the equation , where

We attempt to find by inspection, or trial-and-error, two values of x, call them and , such that and have different signs, i.e., . If we can find two such values, the root must lie somewhere in the interval between them, since changes sign on this interval (see Figure 14.3). In this example, and will do, since and . In the Bisection method, we estimate the root by , where is the midpoint of the interval , i.e.,

(14.1)

Then if has the same sign as , as drawn in the figure, the root clearly lies between and . We must then redefine the left-hand end of the interval as having the value of , i.e., we let the new value of be . Otherwise, if and have different signs, we let the new value of be , since the root must lie between and in that case. Having redefined or , as the case may be, we bisect the new interval again according to Equation (14.1) and repeat the process until the distance between and is as small as we please.

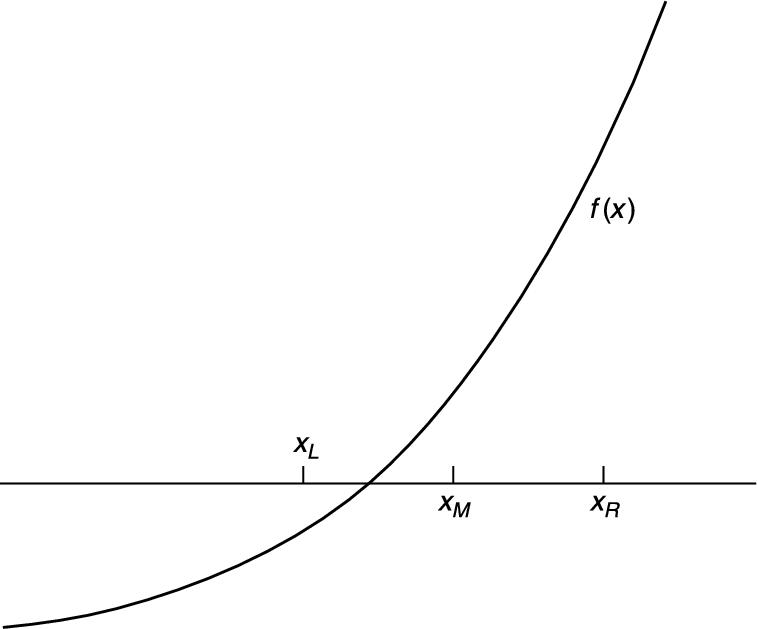
FIGURE 14.3 The Bisection method.

The neat thing about this method is that, before starting, we can calculate how many bisections are needed to obtain a certain accuracy, given initial values of and . Suppose we start with , and . After the first bisection the worst possible error () in is , since we are estimating the root as being at the midpoint of the interval . The worst that can happen is that the root is actually at or , in which case the error is . Carrying on like this, after n bisections the worst possible error is given by . If we want to be sure that this is less than some specified error E, we must see to it that n satisfies the inequality , i.e.,

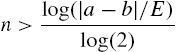(14.2)

Since n is the number of bisections, it must be an integer. The smallest integer n that exceeds the right-hand side of Inequality (14.2) will do as the maximum number of bisections required to guarantee the given accuracy E.

The following scheme may be used to program the Bisection method. It will work for any function that changes sign (in either direction) between the two values a and b, which must be found beforehand by the user.

1. Input and E

2. Initialize and

3. Compute maximum bisections n from Inequality (14.2)

4. Repeat n times:

Compute according to Equation (14.1)

If then

Let

otherwise

Let

5. Display root

6. Stop.

We have assumed that the procedure will not find the root exactly; the chances of this happening with real variables are infinitesimal.

The main advantage of the Bisection method is that it is guaranteed to find a root if you can find two starting values for and between which the function changes sign. You can also compute in advance the number of bisections needed to attain a given accuracy. Compared to Newton's method it is inefficient. Successive bisections do not necessarily move closer to the root, as usually happens with Newton's method. In fact, it is interesting to compare the two methods on the same function to see how many more steps the Bisection method requires than Newton's method. For example, to solve the equation , the Bisection method takes 21 steps to reach the same accuracy as Newton's in five steps.

14.1.3. fzero

The MATLAB function fzero(@f, a) finds the zero nearest to the value a of the function f represented by the function f.m.

Use it to find a zero of .

fzero doesn't appear to be able to find complex roots.

14.1.4. roots

The MATLAB function M-file roots(c) finds all the roots (zeros) of the polynomial with coefficients in the vector c. See help for details.

Use it to find a zero of .

14.2. Integration

Although most ‘respectable’ mathematical functions can be differentiated analytically, the same cannot be said for integration. There are no general rules for integrating, as there are for differentiating. For example, the indefinite integral of a function as simple as cannot be found analytically. We therefore need numerical methods for evaluating integrals.

This is actually quite easy, and depends on the fact that the definite integral of a function between the limits and is equal to the area under bounded by the x-axis and the two vertical lines and . So all numerical methods for integrating simply involve more or less ingenious ways of estimating the area under .

14.2.1. The Trapezoidal rule

The Trapezoidal (or Trapezium) rule is fairly simple to program. The area under is divided into vertical panels each of width h, called the step-length. If there are n such panels, then , i.e., . If we join the points where successive panels cut , we can estimate the area under as the sum of the area of the resulting trapezia (see Figure 14.4). If we call this approximation to the integral S, then

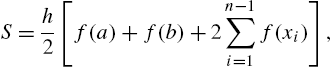(14.3)

where . Equation (14.3) is the Trapezoidal rule, and provides an estimate for the integral

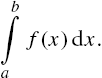
FIGURE 14.4 The Trapezoidal rule.

Here is a function to implement the Trapezoidal rule:

function y = trap( fn, a, b, h )

n = (b-a)/h;

x = a + [1:n-1]*h;

y = sum(feval(fn, x));

y = h/2*(feval(fn, a) + feval(fn, b) + 2*y);

Note:

1. Since the summation in the rule is implemented with a vectorized formula rather than a for loop (to save time), the function to be integrated must use array operators where appropriate in its M-file implementation.

2. The user must choose h in such a way that the number of steps n will be an integer—a check for this could be built in.

As an exercise, integrate between the limits 0 and 4 (remember to write x.^3 in the function M-file). Call trap as follows:

s = trap(@f, 0, 4, h);

With , the estimate is 64.04, and with it is 64.0004 (the exact integral is 64). You will find that as h gets smaller, the estimate gets more accurate.

This example assumes that is a continuous function which may be evaluated at any x. In practice, the function could be defined at discrete points supplied as results of an experiment. For example, the speed of an object might be measured every so many seconds, and one might want to estimate the distance traveled as the area under the speed-time graph. In this case, trap would have to be changed by replacing fn with a vector of function values. This is left as an exercise for the curious. Alternatively, you can use the MATLAB function interp1 to interpolate the data. See help.

14.2.2. Simpson's rule

Simpson's rule is a method of numerical integration which is a good deal more accurate than the Trapezoidal rule, and should always be used before you try anything fancier. It also divides the area under the function to be integrated, , into vertical strips, but instead of joining the points with straight lines, every set of three such successive points is fitted with a parabola. To ensure that there are always an even number of panels, the step-length h is usually chosen so that there are 2n panels, i.e., .

Using the same notation as above, Simpson's rule estimates the integral as

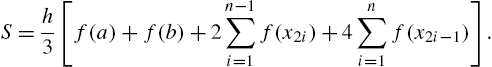(14.4)

Coding this formula into a function M-file is left as an exercise.

If you try Simpson's rule on between any limits, you will find rather surprisingly, that it gives the same result as the exact mathematical solution. This is a nice extra benefit of the rule: it integrates cubic polynomials exactly (which can be proved).

14.2.3. quad

Not surprisingly, MATLAB has a function quad to carry out numerical integration, or quadrature as it is also called. See help.

You may think there is no point in developing our own function files to handle these numerical procedures when MATLAB has its own. If you have got this far, you should be curious enough to want to know how they work, rather than treating them simply as ‘black boxes’.

14.3. Numerical differentiation

The Newton quotient for a function is given by

(14.5)

where h is ‘small’. As h tends to zero, this quotient approaches the first derivative, . The Newton quotient may therefore be used to estimate a derivative numerically. It is a useful exercise to do this with a few functions for which you know the derivatives. This way you can see how small you can make h before rounding errors cause problems. Such errors arise because expression (14.5) involves subtracting two terms that eventually become equal when the limit of the computer's accuracy is reached.

As an example, the following script uses the Newton quotient to estimate for (which must be supplied as a function file f.m) at , for smaller and smaller values of h (the exact answer is 4).

h = 1;

x = 2;

format short e

for i = 1:20

nq = (f(x+h) - f(x))/h;

disp( [h nq] )

h = h / 10;

end

Output:

1 5

1.0000e-001 4.1000e+000

1.0000e-002 4.0100e+000

1.0000e-003 4.0010e+000

1.0000e-004 4.0001e+000

1.0000e-005 4.0000e+000

1.0000e-006 4.0000e+000

1.0000e-007 4.0000e+000

1.0000e-008 4.0000e+000

1.0000e-009 4.0000e+000

1.0000e-010 4.0000e+000

1.0000e-011 4.0000e+000

1.0000e-012 4.0004e+000

1.0000e-013 3.9968e+000

1.0000e-014 4.0856e+000

1.0000e-015 3.5527e+000

1.0000e-016 0

...

The results show that the best h for this particular problem is about . But for h much smaller than this the estimate becomes totally unreliable.

Generally, the best h for a given problem can only be found by trial and error. Finding it can be a non-trivial exercise. This problem does not arise with numerical integration, because numbers are added to find the area, not subtracted.

14.3.1. diff

If x is a row or column vector

[x(1) x(2) ... x(n)]

then the MATLAB function diff(x) returns a vector of differences between adjacent elements:

[x(2)-x(1) x(3)-x(2) ... x(n)-x(n-1)]

The output vector is one element shorter than the input vector.

In certain problems, diff is helpful in finding approximate derivatives, e.g., if x contains displacements of an object every h seconds, diff(x)/h will be its speed.

14.4. First-order differential equations

The most interesting situations in real life that we may want to model, or represent quantitatively, are usually those in which the variables change in time (e.g., biological, electrical or mechanical systems). If the changes are continuous, the system can often be represented with equations involving the derivatives of the dependent variables. Such equations are called differential equations. The main aim of a lot of modeling is to be able to write down a set of differential equations (DEs) that describe the system being studied as accurately as possible. Very few DEs can be solved analytically, so once again, numerical methods are required. We will consider the simplest method of numerical solution in this section: Euler's method (Euler rhymes with ‘boiler’). We also consider briefly how to improve it.

14.4.1. Euler's method

In general we want to solve a first-order DE (strictly an ordinary—ODE) of the form

Euler's method for solving this DE numerically consists of replacing with its Newton quotient, so that the DE becomes

After a slight rearrangement of terms, we get

(14.6)

Solving a DE numerically is such an important and common problem in science and engineering that it is worth introducing some general notation at this point. Suppose we want to integrate the DE over the interval ( usually) to . We break this interval up into m steps of length h, so

(this is the same as the notation used in the update process of Chapter 10, except that dt used there has been replaced by the more general h here).

For consistency with MATLAB's subscript notation, if we define as (the Euler estimate at the beginning of step i), where , then , at the end of step i. We can then replace Equation (14.6) by the iterative scheme

(14.7)

where . Recall from Chapter 10 that this notation enables us to generate a vector y which we can then plot. Note also the striking similarity between Equation (14.7) and the equation in Chapter 10 representing an update process. This similarity is no coincidence. Update processes are typically modeled by DEs, and Euler's method provides an approximate solution for such DEs.

14.4.2. Example: bacteria growth

Suppose a colony of 1000 bacteria is multiplying at the rate of per hour per individual (i.e. an individual produces an average of 0.8 offspring every hour). How many bacteria are there after 10 hours? Assuming that the colony grows continuously and without restriction, we can model this growth with the DE

(14.8)

where is the population size at time t. This process is called exponential growth. Equation (14.8) may be solved analytically to give the well-known formula for exponential growth:

To solve Equation (14.8) numerically, we apply Euler's algorithm to it to get

(14.9)

where the initial value .

It is very easy to program Euler's method. The following script implements Equation (14.9), taking . It also computes the exact solution for comparison.

h = 0.5;

r = 0.8;

a = 0;

b = 10;

m = (b - a) / h;

N = zeros(1, m+1);

N(1) = 1000;

t = a:h:b;

for i = 1:m

N(i+1) = N(i) + r * h * N(i);

end

Nex = N(1) * exp(r * t);

format bank

disp( [t' N' Nex'] )

plot(t, N ), xlabel( 'Hours' ), ylabel( 'Bacteria' )

hold on

plot(t, Nex ), hold off

Results are shown in Table 14.1, and also in Figure 14.5. The Euler solution is not too good. In fact, the error gets worse at each step, and after 10 h of bacteria time it is about 72%. The numerical solution will improve if we make h smaller, but there will always be some value of t where the error exceeds some acceptable limit.

Table 14.1

Bacteria Growth

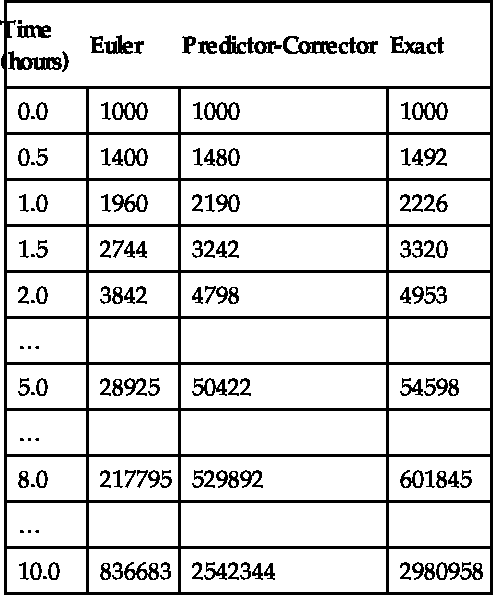
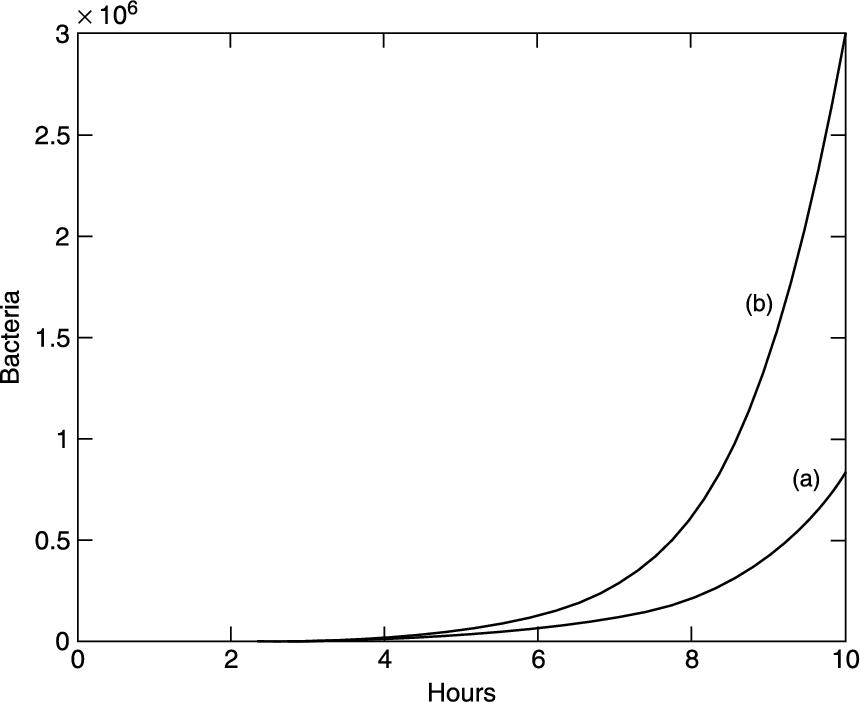
FIGURE 14.5 Bacteria growth: (a) Euler's method; (b) the exact solution.

In some cases, Euler's method performs better than it does here, but there are other numerical methods which always do better than Euler. Two of them are discussed below. More sophisticated methods may be found in most textbooks on numerical analysis. However, Euler's method may always be used as a first approximation as long as you realize that errors may arise.

14.4.3. Alternative subscript notation

Equation (14.9) is an example of a finite difference scheme. The conventional finite difference notation is for the initial value to be represented by , i.e. with subscript . is then the estimate at the end of step i. If you want the MATLAB subscripts in the Euler solution to be the same as the finite difference subscripts, the initial value must be represented by the MATLAB scalar N0, and you have to compute N(1) separately, before the for loop starts. You also have to display or plot the initial values separately since they will no longer be included in the MATLAB vectors t, N and Nex (which now have m instead of elements). Here is a complete script to generate the Euler solution using finite difference subscripts:

h = 0.5;

r = 0.8;

a = 0;

b = 10;

m = (b - a) / h;

N = zeros(1, m); % one less element now

N0 = 1000;

N(1) = N0 + r*h*N0; % no longer 'self-starting'

for i = 2:m

N(i) = N(i-1) + r * h * N(i-1); %finite difference notation

end

t = a+h:h:b; % exclude initial time = a

Nex = N0 * exp(r * t);

disp( [a N0 N0] ) % display initial values separately

disp( [t' N' Nex'] )

plot(a, N0) % plot initial values separately

hold on

plot(t, N ), xlabel( 'Hours' ), ylabel( 'Bacteria' )

plot(t, Nex ), hold off

14.4.4. A predictor-corrector method

One improvement on the numerical solution of the first-order DE

is as follows. The Euler approximation, which we are going to denote by an asterisk, is given by

(14.10)

But this formula favors the old value of y in computing on the right-hand side. Surely it would be better to say

(14.11)

where , since this also involves the new value in computing f on the right-hand side? The problem of course is that is as yet unknown, so we can't use it on the right-hand side of Equation (14.11). But we could use Euler to estimate (predict) from Equation (14.10) and then use Equation (14.11) to correct the prediction by computing a better version of , which we will call . So the full procedure is:

Repeat as many times as required:
	Use Euler to predict:
	Then correct to: .

This is called a predictor-corrector method. The script above can easily be adapted to this problem. The relevant lines of code are:

for i = 1:m % m steps of length dt

ne(i+1) = ne(i) + r * h * ne(i);

np = nc(i) + r * h * nc(i);

nc(i+1) = nc(i) + r * h * (np + nc(i))/2;

disp( [t(i+1) ne(i+1) nc(i+1) nex(i+1)] )

end;

ne stands for the ‘straight’ (uncorrected) Euler solution, np is the Euler predictor (since this is an intermediate result a vector is not needed for np), and nc is the corrector. The worst error is now only 15%. This is much better than the uncorrected Euler solution, although there is still room for improvement.

14.5. Linear ordinary differential equations (LODEs)

Linear ODEs with constant coefficients may be solved analytically in terms of matrix exponentials, which are represented in MATLAB by the function expm. For an example see MATLAB Help: Mathematics: Matrices and Linear Algebra: Matrix Powers and Exponentials.

14.6. Runge-Kutta methods

There are a variety of algorithms, under the general name of Runge-Kutta, which can be used to integrate systems of ODEs. The formulae involved are rather complicated; they can be found in most books on numerical analysis.

However, as you may have guessed, MATLAB has plenty of ODE solvers, which are discussed in MATLAB Help: Mathematics: Differential Equations. Among them are ode23 (second/third order) and ode45 (fourth/fifth order), which implement Runge-Kutta methods. (The order of a numerical method is the power of h (i.e., dt) in the leading error term. Since h is generally very small, the higher the power, the smaller the error.) We will demonstrate the use of ode23 and ode45 here, first with a single first-order DE, and then with systems of such equations.

14.6.1. A single differential equation

Here's how to use ode23 to solve the bacteria growth problem, Equation (14.8):

1. Start by writing a function file for the right-hand side of the DE to be solved. The function must have input variables t and N in this case (i.e., independent and dependent variables of the DE), in that order, e.g., create the function file f.m as follows:

function y = f(t, Nr)

y = 0.8 * Nr;

2. Now enter the following statements in the Command Window:

a = 0;

b = 10;

n0 = 1000;

[t, Nr] = ode23(@f, [a:0.5:b], n0);

3. Note the input arguments of ode23:

@f: a handle for the function f, which contains the right-hand side of the DE;

[a:0.5:b]: a vector (tspan) specifying the range of integration. If tspan has two elements ([a b]) the solver returns the solution evaluated at every integration step (the solver chooses the integration steps and may vary them). This form would be suitable for plotting. However, if you want to display the solution at regular time intervals, as we want to here, use the form of tspan with three elements as above. The solution is then returned evaluated at each time in tspan. The accuracy of the solution is not affected by the form of tspan used.

n0: the initial value of the solution N.

4. The output arguments are two vectors: the solutions Nr at times t. For 10 h ode23 gives a value of 2961338 bacteria. From the exact solution in Table 14.1 we see that the error here is only 0.7%.

If the solutions you get from ode23 are not accurate enough, you can request greater accuracy with an additional optional argument. See help.

If you need still more accurate numerical solutions, you can use ode45 instead. It gives a final value for the bacteria of 2981290—an error of about 0.01%.

14.6.2. Systems of differential equations: chaos

The reason that weather prediction is so difficult and forecasts are so erratic is no longer thought to be the complexity of the system but the nature of the DEs modeling it. These DEs belong to a class referred to as chaotic. Such equations will produce wildly different results when their initial conditions are changed infinitesimally. In other words, accurate weather prediction depends crucially on the accuracy of the measurements of the initial conditions.

Edward Lorenz, a research meteorologist, discovered this phenomenon in 1961. Although his original equations are far too complex to consider here, the following much simpler system has the same essential chaotic features:

(14.12)

(14.13)

(14.14)

This system of DEs may be solved very easily with the MATLAB ODE solvers. The idea is to solve the DEs with certain initial conditions, plot the solution, then change the initial conditions very slightly, and superimpose the new solution over the old one to see how much it has changed.

We begin by solving the system with the initial conditions , and .

1. Write a function file lorenz.m to represent the right-hand sides of the system as follows:

function f = lorenz(t, x)

f = zeros(3,1);

f(1) = 10 * (x(2) - x(1));

f(2) = -x(1) * x(3) + 28 * x(1) - x(2);

f(3) = x(1) * x(2) - 8 * x(3) / 3;

The three elements of the MATLAB vector x, i.e., x(1), x(2) and x(3), represent the three dependent scalar variables x, y and z respectively. The elements of the vector f represent the right-hand sides of the three DEs. When a vector is returned by such a DE function it must be a column vector, hence the statement

f = zeros(3,1);

2. Now use the following commands to solve the system from to , say:

x0 = [-2 -3.5 21]; % initial values in a vector

[t, x] = ode45(@lorenz, [0 10], x0);

plot(t,x)

Note that we are use ode45 now, since it is more accurate.

You will see three graphs, for x, y and z (in different colors).

3. It's easier to see the effect of changing the initial values if there is only one graph in the figure to start with. It is in fact best to plot the solution on its own.

The MATLAB solution x is actually a matrix with three columns (as you can see from whos). The solution that we want will be the second column, so to plot it by itself use the command

plot(t,x(:,2),'g')

Then keep the graph on the axes with the command hold.

Now we can see the effect of changing the initial values. Let's just change the initial value of , from −2 to −2.04—that's a change of only 2%, and in only one of the three initial values. The following commands will do this, solve the DEs, and plot the new graph of (in a different color):

x0 = [-2.04 -3.5 21];

[t, x] = ode45(@lorenz, [0 10], x0);

plot(t,x(:,2),'r')

You should see (Figure 14.6) that the two graphs are practically indistinguishable until t is about 1.5. The discrepancy grows quite gradually, until t reaches about 6, when the solutions suddenly and shockingly flip over in opposite directions. As t increases further, the new solution bears no resemblance to the old one.

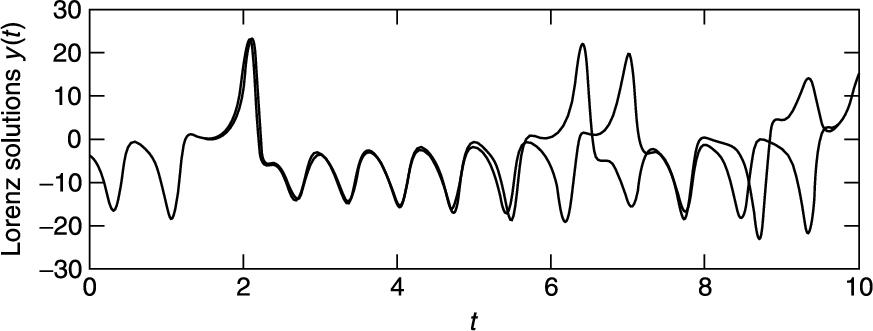
FIGURE 14.6 Chaos?

Now solve the system (14.12)–(14.14) with the original initial values using ode23 this time:

x0 = [-2 -3.5 21];

[t,x] = ode23(@lorenz, [0 10], x0);

Plot the graph of only—x(:,2)—and then superimpose the ode45 solution with the same initial values (in a different color).

A strange thing happens—the solutions begin to deviate wildly for ! The initial conditions are the same—the only difference is the order of the Runge-Kutta method.

Finally solve the system with ode23s and superimpose the solution. (The s stands for ‘stiff’. For a stiff DE, solutions can change on a time scale that is very short compared to the interval of integration.) The ode45 and ode23s solutions only start to diverge at .

The explanation is that ode23, ode23s and ode45 all have numerical inaccuracies (if one could compare them with the exact solution—which incidentally can't be found). However, the numerical inaccuracies are different in the three cases. This difference has the same effect as starting the numerical solution with very slightly different initial values.

How do we ever know when we have the ‘right’ numerical solution? Well, we don't—the best we can do is increase the accuracy of the numerical method until no further wild changes occur over the interval of interest. So in our example we can only be pretty sure of the solution for (using ode23s or ode45). If that's not good enough, you have to find a more accurate DE solver.

So beware: ‘chaotic’ DEs are very tricky to solve!

Incidentally, if you want to see the famous ‘butterfly’ picture of chaos, just plot x against z as time increases (the resulting graph is called a phase plane plot). The following command will do the trick:

plot(x(:,1), x(:,3))

What you will see is a static 2-D projection of the trajectory, i.e., the solution developing in time. Demos in the MATLAB Launch Pad include an example which enables you to see the trajectory evolving dynamically in 3-D (Demos: Graphics: Lorenz attractor animation).

14.6.3. Passing additional parameters to an ODE solver

In the above examples of the MATLAB ODE solvers the coefficients in the right-hand sides of the DEs (e.g., the value 28 in Equation (14.13)) have all been constants. In a real modeling situation, you will most likely want to change such coefficients frequently. To avoid having to edit the function files each time you want to change a coefficient, you can pass the coefficients as additional parameters to the ODE solver, which in turn passes them to the DE function. To see how this may be done, consider the Lotka-Volterra predator-prey model:

(14.15)

(14.16)

where and are the prey and predator population sizes at time t, and p, q, r and s are biologically determined parameters. For this example, we take , , , , and .

First, write a function M-file, volterra.m as follows:

function f = volterra(t, x, p, q, r, s)

f = zeros(2,1);

f(1) = p*x(1) - q*x(1)*x(2);

f(2) = r*x(1)*x(2) - s*x(2);

Then enter the following statements in the Command Window, which generate the characteristically oscillating graphs in Figure 14.7:

p = 0.4; q = 0.04; r = 0.02; s = 2;

[t,x] = ode23(@volterra,[0 10],[105; 8],[],p,q,r,s);

plot(t, x)

Note:

■ The additional parameters (p, q, r and s) have to follow the fourth input argument (options—see help) of the ODE solver. If no options have been set (as in our case), use [] as a placeholder for the options parameter.

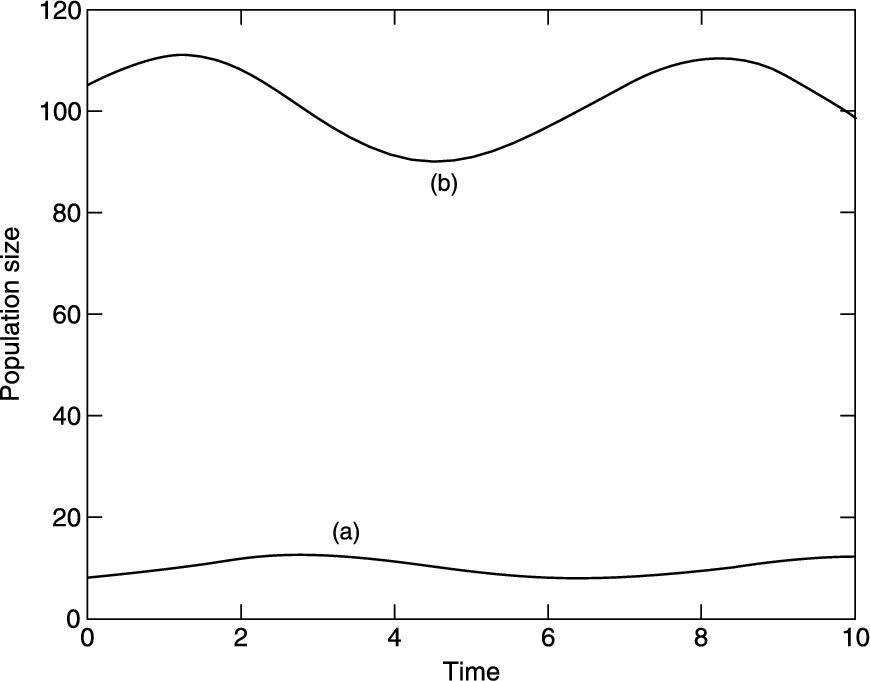
FIGURE 14.7 Lotka-Volterra model: (a) predator; (b) prey.

You can now change the coefficients from the Command Window and get a new solution, without editing the function file.

14.7. A partial differential equation

The numerical solution of partial differential equations (PDEs) is a vast subject, which is beyond the scope of this book. However, a class of PDEs called parabolic often lead to solutions in terms of sparse matrices, which were mentioned briefly in Chapter 6. One such example is considered in this section.

14.7.1. Heat conduction

The conduction of heat along a thin uniform rod may be modeled by the partial differential equation

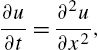(14.17)

where is the temperature distribution a distance x from one end of the rod at time t, and assuming that no heat is lost from the rod along its length.

Half the battle in solving PDEs is mastering the notation. We set up a rectangular grid, with step-lengths of h and k in the x and t directions respectively. A general point on the grid has co-ordinates , . A concise notation for at , is then simply .

Truncated Taylor series may then be used to approximate the PDE by a finite difference scheme. The left-hand side of Equation (14.17) is usually approximated by a forward difference:

One way of approximating the right-hand side of Equation (14.17) is by the scheme

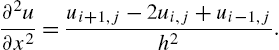(14.18)

This leads to a scheme, which although easy to compute, is only conditionally stable.

If however we replace the right-hand side of the scheme in Equation (14.18) by the mean of the finite difference approximation on the jth and th time rows, we get (after a certain amount of algebra!) the following scheme for Equation (14.17):

(14.19)

where . This is known as the Crank-Nicolson implicit method, since it involves the solution of a system of simultaneous equations, as we shall see.

To illustrate the method numerically, let's suppose that the rod has a length of 1 unit, and that its ends are in contact with blocks of ice, i.e., the boundary conditions are

(14.20)

Suppose also that the initial temperature (initial condition) is

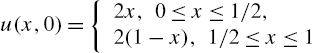(14.21)

(this situation could come about by heating the center of the rod for a long time, with the ends kept in contact with the ice, removing the heat source at time ). This particular problem has symmetry about the line ; we exploit this now in finding the solution.

If we take and , we will have , and Equation (14.19) becomes

(14.22)

Putting in Equation (14.22) generates the following set of equations for the unknowns (i.e., after one time step k) up to the midpoint of the rod, which is represented by , i.e., . The subscript has been dropped for clarity:

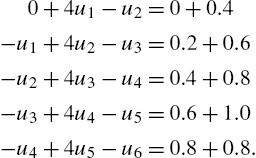
Symmetry then allows us to replace in the last equation by . These equations can be written in matrix form as

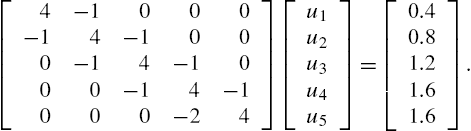(14.23)

The matrix (A) on the left of Equations (14.23) is known as a tridiagonal matrix. Having solved for the we can then put in Equation (14.22) and proceed to solve for the , and so on. The system (14.23) can of course be solved directly in MATLAB with the left division operator. In the script below, the general form of Equations (14.23) is taken as

(14.24)

Care needs to be taken when constructing the matrix A. The following notation is often used:

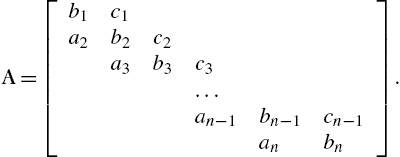
A is an example of a sparse matrix (see Chapter 6).

The script below implements the general Crank-Nicolson scheme of Equation (14.19) to solve this particular problem over 10 time steps of . The step-length is specified by because of symmetry. r is therefore not restricted to the value 1, although it takes this value here. The script exploits the sparsity of A by using the sparse function.

format compact

n = 5;

k = 0.01;

h = 1 / (2 * n); % symmetry assumed

r = k / h ^ 2;

% set up the (sparse) matrix A

b = sparse(1:n, 1:n, 2+2*r, n, n); % b(1) .. b(n)

c = sparse(1:n-1, 2:n, -r, n, n); % c(1) .. c(n-1)

a = sparse(2:n, 1:n-1, -r, n, n); % a(2) ..

A = a + b + c;

A(n, n-1) = -2 * r; % symmetry: a(n)

full(A) %

disp(' ')

u0 = 0; % boundary condition (Eq 14.20)

u = 2*h*[1:n] % initial conditions (Eq 14.21)

u(n+1) = u(n-1); % symmetry

disp([0 u(1:n)])

for t = k*[1:10]

g = r * ([u0 u(1:n-1)] + u(2:n+1)) ...

+ (2 - 2 * r) * u(1:n); % Eq 14.19

v = A\g'; % Eq 14.24

disp([t v'])

u(1:n) = v;

u(n+1) = u(n-1); % symmetry

end

Note:

■ to preserve consistency between the formal subscripts of Equation (14.19) etc. and MATLAB subscripts, (the boundary value) is represented by the scalar u0.

In the following output the first column is time, and subsequent columns are the solutions at intervals of h along the rod:

0 0.2000 0.4000 0.6000 0.8000 1.0000

0.0100 0.1989 0.3956 0.5834 0.7381 0.7691

0.0200 0.1936 0.3789 0.5397 0.6461 0.6921

...

0.1000 0.0948 0.1803 0.2482 0.2918 0.3069

MATLAB has some built-in PDE solvers. See MATLAB Help: Mathematics: Differential Equations: Partial Differential Equations.

14.8. Complex variables and conformal mapping

In this section one application of the complex-variable capabilities in MATLAB is demonstrated. It is the transformation of a circle to a Joukowski airfoil.

Joukowski airfoil

The solution of the flow around a circular cylinder with circulation in a cross flow can be used to predict the flow around thin airfoils. We can transform the local geometry of the cylinder into an ellipse, an airfoil or a flat plate without influencing the geometry in the far field. This procedure is known as conformal mapping. If we interpret the Cartesian coordinates as the coordinates of the plane of complex numbers , where x and y are real numbers, , x is the real part of z and y is the imaginary part of z, then doing this allows us to use complex variable theory to solve two-dimensional potential flow problems. We are not going to examine complex variable theory here. Instead, we will give an example of the application of one of the ideas to illustrate that the circle can be transformed into an airfoil. Table 14.2 is a MATLAB script that does this. MATLAB is very useful for this problem because it does complex arithmetic. The steps are outlined in the table. The result of executing this code is illustrated in Figure 14.8. The figure shows the circle and the airfoil that is mapped from it. Each point on the circle corresponds to a unique point on the airfoil. The potential at each point on the cylinder is the same as the corresponding point on the airfoil. This is how the solution of the circle problem is mapped to solve the flow around the airfoil. What is different is the distance between points and, hence, the velocity and pressure distributions on the airfoil must be determined from the mapped distribution of the potential. The far field is not affected by the transformation.

Table 14.2

MATLAB File Used to Produce Figure 14.8

% Joukowski transformation MATLAB code

% Example of conformal mapping of a circle to an airfoil

% AE425-ME425 Aerodynamics

% Daniel T. Valentine .................... January 2009

% Circle in (xp,yp) plane: R = sqrt(xp^2 + yp^2), R > 1

% Complex variables of three complex planes of interest:

% zp = xp + i*yp ==> Circle plane

% z = x + i*y ==> Intermediate plane

% w = u + i*v ==> Airfoil (or physical) plane

clear;clc

% Step 1: Select the parameters that define the airfoil of interest.

% (1) Select the a == angle of attack alpha

a = -2; % in degrees

a = a*pi/180; % Conversion to radians

% (2) Select the parameter related to thichkness of the airfoil:

e = .1;

% (3) Select the shift of y-axis related to camber of the airfoil:

f = .1;

% (4) Select the trailing edge angle parameter:

te = .05; % 0 < te < 1 (0 ==> cusped trailing edge)

n = 2 - te; % Number related to trailing edge angle.

tea = (n^2-1)/3; % This is a Karman-Trefftz extension.

% Step 2: Compute the coordinates of points on circle in zp-plane:

R = 1 + e;

theta = 0:pi/200:2*pi;

yp = R * sin(theta);

xp = R * cos(theta);

% Step 3: Transform coordinates of circle from zp-plane to z-plane:

z = (xp - e) + i.*(yp + f);

% Step 4: Transform circle from z-plane to airfoil in w-plane

% (the w-plane is the "physical" plane of the airfoil):

rot = exp(i*a); % Application of angle of attack.

w = rot .* (z + tea*1./z); % Joukowski transformation.

% Step 5: Plot of circle in z-plane on top of airfoil in w-plane

plot(xp,yp), hold on

plot(real(w),imag(w),'r'),axis image, hold off

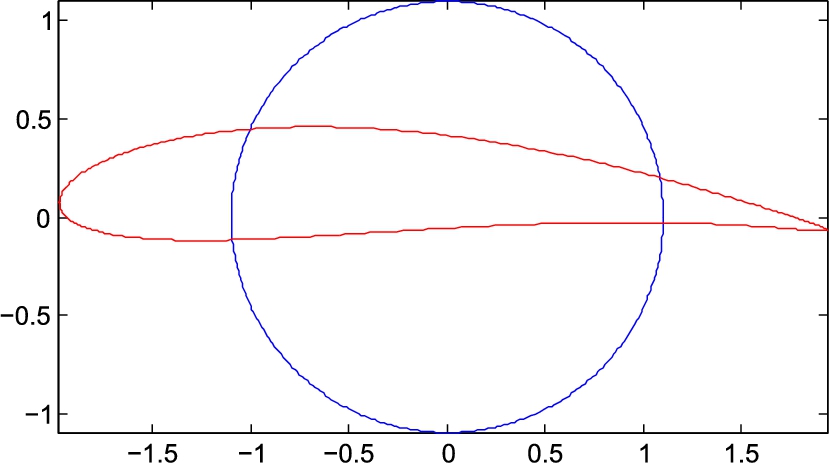
FIGURE 14.8 Map of circle to an airfoil: illustration of the application of the Joukowski transformation in the complex plane.

14.9. Other numerical methods

The ODEs considered earlier in this chapter are all initial value problems. For boundary value problem solvers, see MATLAB Help: Mathematics: Differential Equations: Boundary Value Problems for ODEs.

MATLAB has a large number of functions for handling other numerical procedures, such as curve fitting, correlation, interpolation, minimization, filtering and convolution, and (fast) Fourier transforms. Consult MATLAB Help: Mathematics: Polynomials and Interpolation and Data Analysis and Statistics.

Here's an example of curve fitting. The following script enables you to plot data points interactively. When you have finished plotting points (signified when the x coordinates of your last two points differ by less than 2 in absolute value) a cubic polynomial is fitted and drawn (see Figure 14.9).

% Interactive script to fit a cubic to data points

clf

hold on

axis([0 100 0 100]);

diff = 10;

xold = 68;

i = 0;

xp = zeros(1); % data points

yp = zeros(1);

while diff > 2

[a b] = ginput(1);

diff = abs(a - xold);

if diff > 2

i = i + 1;

xp(i) = a;

yp(i) = b;

xold = a;

plot(a, b, 'ok')

end

p = polyfit(xp, yp, 3 );

x = 0:0.1:xp(length(xp));

y= p(1)*x.^3 + p(2)*x.^2 + p(3)*x + p(4);

plot(x,y), title( 'cubic polynomial fit'), ...

ylabel('y(x)'), xlabel('x')

hold off

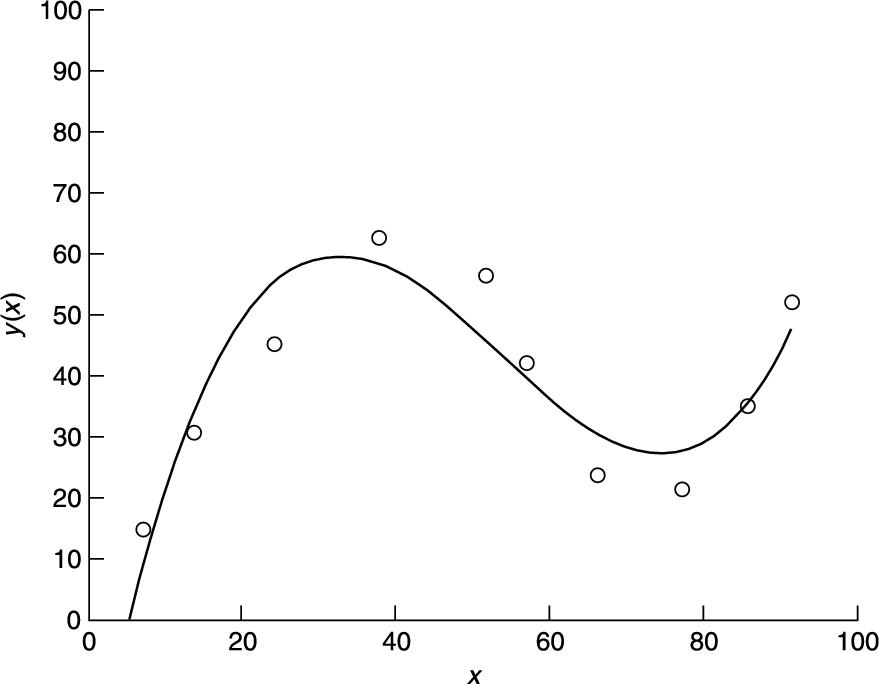
FIGURE 14.9 A cubic polynomial fit.

Polynomial fitting may also be done interactively in a figure window, with Tools -> Basic Fitting.

Summary

■ A numerical method is an approximate computer method for solving a mathematical problem which often has no analytical solution.

■ A numerical method is subject to two distinct types of error: rounding error in the computer solution, and truncation error, where an infinite mathematical process, like taking a limit, is approximated by a finite process.

■ MATLAB has a large number of useful functions for handling numerical methods.

Exercises

14.1 Use Newton's method in a script to solve the following (you may have to experiment a bit with the starting values). Check all your answers with fzero. Check the answers involving polynomial equations with roots.

Hint: use fplot to get an idea of where the roots are, e.g.,

fplot('x^3-8*x^2+17*x-10', [0 3])

The Zoom feature also helps. In the figure window select the Zoom In button (magnifying glass) and click on the part of the graph you want to magnify.

(a) (two real roots and two complex roots)

(b) (infinitely many roots)

(d)

(e) (four real roots)

14.2 Use the Bisection method to find the square root of 2, taking 1 and 2 as initial values of and . Continue bisecting until the maximum error is less than 0.05 (use Inequality (14.2) of Section 14.1 to determine how many bisections are needed).

14.3 Use the Trapezoidal rule to evaluate , using a step-length of .

14.4 A human population of 1000 at time grows at a rate given by

where per person per year. Use Euler's method to project the population over the next 30 years, working in steps of (a) years, (b) year and (c) years. Compare your answers with the exact mathematical solution.

14.5 Write a function file euler.m which starts with the line

function [t, n] = euler(a, b, dt)

and which uses Euler's method to solve the bacteria growth DE (14.8). Use it in a script to compare the Euler solutions for and 0.05 with the exact solution. Try to get your output looking like this:

time dt = 0.5 dt = 0.05 exact

0 1000.00 1000.00 1000.00

0.50 1400.00 1480.24 1491.82

1.00 1960.00 2191.12 2225.54

...

5.00 28925.47 50504.95 54598.15

14.6 The basic equation for modeling radio-active decay is

where x is the amount of the radio-active substance at time t, and r is the decay rate.

Some radio-active substances decay into other radio-active substances, which in turn also decay. For example, Strontium 92 ( per hr) decays into Yttrium 92 ( per hr), which in turn decays into Zirconium. Write down a pair of differential equations for Strontium and Yttrium to describe what is happening.

Starting at with atoms of Strontium 92 and none of Yttrium, use the Runge-Kutta method (ode23) to solve the equations up to in steps of 1/3 hr. Also use Euler's method for the same problem, and compare your results.

14.7 The springbok (a species of small buck, not rugby players!) population in the Kruger National Park in South Africa may be modeled by the equation

where r, b, and a are constants. Write a program which reads values for r, b, and a, and initial values for x and t, and which uses Euler's method to compute the impala population at monthly intervals over a period of two years.

14.8 The luminous efficiency (ratio of the energy in the visible spectrum to the total energy) of a black body radiator may be expressed as a percentage by the formula

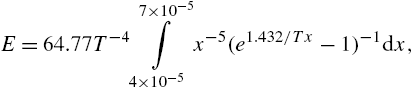
where T is the absolute temperature in degrees Kelvin, x is the wavelength in cm, and the range of integration is over the visible spectrum.

Write a general function simp(fn, a, b, h) to implement Simpson's rule as given in Equation (14.4).

Taking , use simp to compute E, firstly with 10 intervals (), and then with 20 intervals (), and compare your results.

(Answers: 14.512725% for ; 14.512667% for )

14.9 Van der Pol's equation is a second-order non-linear differential equation which may be expressed as two first-order equations as follows:

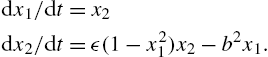
The solution of this system has a stable limit cycle, which means that if you plot the phase trajectory of the solution (the plot of against ) starting at any point in the positive plane, it always moves continuously into the same closed loop. Use ode23 to solve this system numerically, for , and . Draw some phase trajectories for and ϵ ranging between 0.01 and 1.0. Figure 14.10 shows you what to expect.

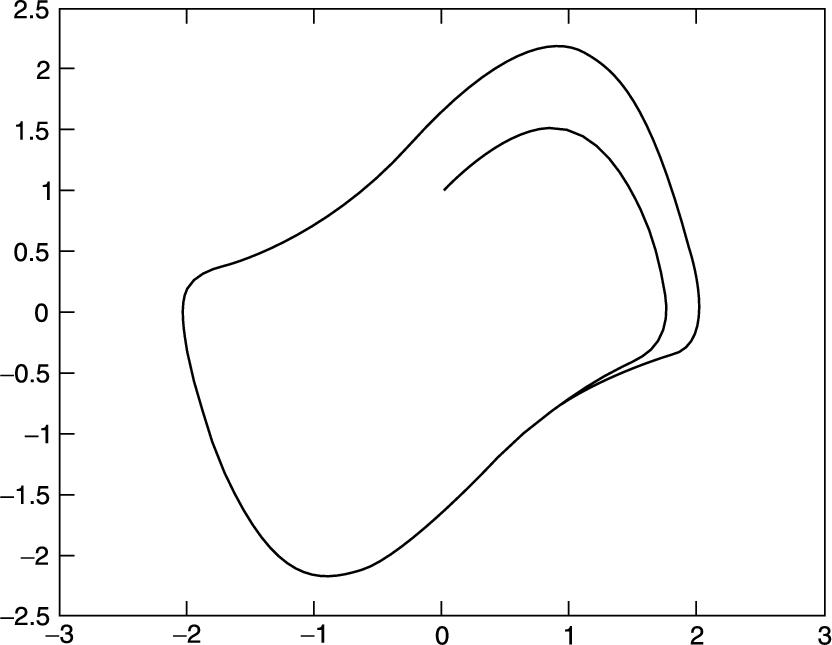
FIGURE 14.10 A trajectory of Van der Pol's equation.