Computer Organization and Design (2016)
Large and Fast
Exploiting Memory Hierarchy
This chapter describes how a memory hierarchy exploits locality. It shows how the principle of locality gives designers a way to overcome the long latency of memory access. It explains how strategies to exploit locality can be used at all levels of the memory hierarchy. The chapter concludes by emphasizing that memory systems are a central design issue for parallel processors, and that the growing importance of the memory hierarchy in determining system performance means that this important area will continue to be a focus of both designers and researchers for some years to come.
Keywords
cache; cache performance; virtual memory; memory hierarchy; ARM Cortex-A8; Intel Core i7; Intel; temporal locality; spatial locality; memory hierarchy; block; line; hit rate; miss rate; hit time; miss penalty; cache coherence; snooping protocol; direct-mapped cache; tag; valid bit; cache miss; write-through; write buffer; write-back; split cache; fully associative cache; set-associative cache; least recently used; LRU; multilevel cache; global miss rate; local miss rate; virtual memory; virtual machine; physical address; protection; page fault; virtual address; address translation; segmentation; page table; swap space; reference bit; use bit; translation-lookaside buffer; TLB; virtually addressed cache; aliasing; physically addressed cache; supervisor mode; kernel mode; system call; context switch; exception enable; restartable instruction; handler; unmapped; three Cs model; compulsory miss; cold-start miss; capacity miss; conflict miss; collision miss; finite-state machine; next-state function; false sharing; nonblocking cache; prefetching; dependability; reliability; availability; disk storage; flash storage; I/O device; I/O; operating system; file system; array; redundant array; networks; matrix multiply; common case fast
Ideally one would desire an indefinitely large memory capacity such that any particular … word would be immediately available. … We are … forced to recognize the possibility of constructing a hierarchy of memories, each of which has greater capacity than the preceding but which is less quickly accessible.
A. W. Burks, H. H. Goldstine, and J. von Neumann Preliminary Discussion of the Logical Design of an Electronic Computing Instrument, 1946
5.1 Introduction
5.2 Memory Technologies
5.3 The Basics of Caches
5.4 Measuring and Improving Cache Performance
5.5 Dependable Memory Hierarchy
5.6 Virtual Machines
5.7 Virtual Memory
5.8 A Common Framework for Memory Hierarchy
5.9 Using a Finite-State Machine to Control a Simple Cache
5.10 Parallelism and Memory Hierarchies: Cache Coherence
![]() 5.11 Parallelism and Memory Hierarchy: Redundant Arrays of Inexpensive Disks
5.11 Parallelism and Memory Hierarchy: Redundant Arrays of Inexpensive Disks
![]() 5.12 Advanced Material: Implementing Cache Controllers
5.12 Advanced Material: Implementing Cache Controllers
5.13 Real Stuff: The ARM Cortex-A8 and Intel Core i7 Memory Hierarchies
5.14 Going Faster: Cache Blocking and Matrix Multiply
5.15 Fallacies and Pitfalls
5.16 Concluding Remarks
![]() 5.17 Historical Perspective and Further Reading
5.17 Historical Perspective and Further Reading
5.18 Exercises
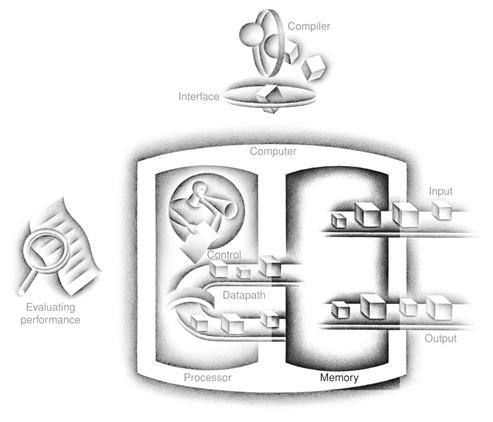
The Five Classic Components of a Computer
5.1 Introduction
From the earliest days of computing, programmers have wanted unlimited amounts of fast memory. The topics in this chapter aid programmers by creating that illusion. Before we look at creating the illusion, let’s consider a simple analogy that illustrates the key principles and mechanisms that we use.
Suppose you were a student writing a term paper on important historical developments in computer hardware. You are sitting at a desk in a library with a collection of books that you have pulled from the shelves and are examining. You find that several of the important computers that you need to write about are described in the books you have, but there is nothing about the EDSAC. Therefore, you go back to the shelves and look for an additional book. You find a book on early British computers that covers the EDSAC. Once you have a good selection of books on the desk in front of you, there is a good probability that many of the topics you need can be found in them, and you may spend most of your time just using the books on the desk without going back to the shelves. Having several books on the desk in front of you saves time compared to having only one book there and constantly having to go back to the shelves to return it and take out another.
The same principle allows us to create the illusion of a large memory that we can access as fast as a very small memory. Just as you did not need to access all the books in the library at once with equal probability, a program does not access all of its code or data at once with equal probability. Otherwise, it would be impossible to make most memory accesses fast and still have large memory in computers, just as it would be impossible for you to fit all the library books on your desk and still find what you wanted quickly.
This principle of locality underlies both the way in which you did your work in the library and the way that programs operate. The principle of locality states that programs access a relatively small portion of their address space at any instant of time, just as you accessed a very small portion of the library’s collection. There are two different types of locality:
■ Temporal locality (locality in time): if an item is referenced, it will tend to be referenced again soon. If you recently brought a book to your desk to look at, you will probably need to look at it again soon.
■ Spatial locality (locality in space): if an item is referenced, items whose addresses are close by will tend to be referenced soon. For example, when you brought out the book on early English computers to find out about the EDSAC, you also noticed that there was another book shelved next to it about early mechanical computers, so you also brought back that book and, later on, found something useful in that book. Libraries put books on the same topic together on the same shelves to increase spatial locality. We’ll see how memory hierarchies use spatial locality a little later in this chapter.
temporal locality
The principle stating that if a data location is referenced then it will tend to be referenced again soon.
spatial locality
The locality principle stating that if a data location is referenced, data locations with nearby addresses will tend to be referenced soon.
Just as accesses to books on the desk naturally exhibit locality, locality in programs arises from simple and natural program structures. For example, most programs contain loops, so instructions and data are likely to be accessed repeatedly, showing high amounts of temporal locality. Since instructions are normally accessed sequentially, programs also show high spatial locality. Accesses to data also exhibit a natural spatial locality. For example, sequential accesses to elements of an array or a record will naturally have high degrees of spatial locality.
We take advantage of the principle of locality by implementing the memory of a computer as a memory hierarchy. A memory hierarchy consists of multiple levels of memory with different speeds and sizes. The faster memories are more expensive per bit than the slower memories and thus are smaller.
memory hierarchy
A structure that uses multiple levels of memories; as the distance from the processor increases, the size of the memories and the access time both increase.
Figure 5.1 shows the faster memory is close to the processor and the slower, less expensive memory is below it. The goal is to present the user with as much memory as is available in the cheapest technology, while providing access at the speed offered by the fastest memory.
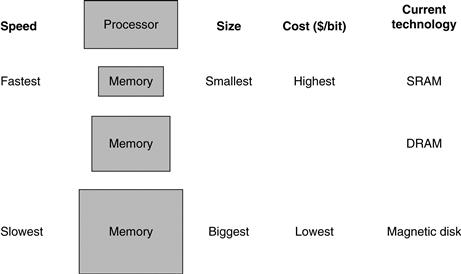
FIGURE 5.1 The basic structure of a memory hierarchy.
By implementing the memory system as a hierarchy, the user has the illusion of a memory that is as large as the largest level of the hierarchy, but can be accessed as if it were all built from the fastest memory. Flash memory has replaced disks in many personal mobile devices, and may lead to a new level in the storage hierarchy for desktop and server computers; see Section 5.2.
The data is similarly hierarchical: a level closer to the processor is generally a subset of any level further away, and all the data is stored at the lowest level. By analogy, the books on your desk form a subset of the library you are working in, which is in turn a subset of all the libraries on campus. Furthermore, as we move away from the processor, the levels take progressively longer to access, just as we might encounter in a hierarchy of campus libraries.
A memory hierarchy can consist of multiple levels, but data is copied between only two adjacent levels at a time, so we can focus our attention on just two levels. The upper level—the one closer to the processor—is smaller and faster than the lower level, since the upper level uses technology that is more expensive. Figure 5.2 shows that the minimum unit of information that can be either present or not present in the two-level hierarchy is called a block or a line; in our library analogy, a block of information is one book.
block (or line)
The minimum unit of information that can be either present or not present in a cache.
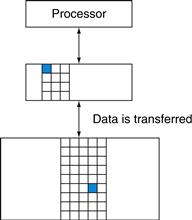
FIGURE 5.2 Every pair of levels in the memory hierarchy can be thought of as having an upper and lower level.
Within each level, the unit of information that is present or not is called a block or a line. Usually we transfer an entire block when we copy something between levels.
If the data requested by the processor appears in some block in the upper level, this is called a hit (analogous to your finding the information in one of the books on your desk). If the data is not found in the upper level, the request is called a miss. The lower level in the hierarchy is then accessed to retrieve the block containing the requested data. (Continuing our analogy, you go from your desk to the shelves to find the desired book.) The hit rate, or hit ratio, is the fraction of memory accesses found in the upper level; it is often used as a measure of the performance of the memory hierarchy. The miss rate (1−hit rate) is the fraction of memory accesses not found in the upper level.
hit rate
The fraction of memory accesses found in a level of the memory hierarchy.
miss rate
The fraction of memory accesses not found in a level of the memory hierarchy.
Since performance is the major reason for having a memory hierarchy, the time to service hits and misses is important. Hit time is the time to access the upper level of the memory hierarchy, which includes the time needed to determine whether the access is a hit or a miss (that is, the time needed to look through the books on the desk). The miss penalty is the time to replace a block in the upper level with the corresponding block from the lower level, plus the time to deliver this block to the processor (or the time to get another book from the shelves and place it on the desk). Because the upper level is smaller and built using faster memory parts, the hit time will be much smaller than the time to access the next level in the hierarchy, which is the major component of the miss penalty. (The time to examine the books on the desk is much smaller than the time to get up and get a new book from the shelves.)
hit time
The time required to access a level of the memory hierarchy, including the time needed to determine whether the access is a hit or a miss.
miss penalty
The time required to fetch a block into a level of the memory hierarchy from the lower level, including the time to access the block, transmit it from one level to the other, insert it in the level that experienced the miss, and then pass the block to the requestor.
As we will see in this chapter, the concepts used to build memory systems affect many other aspects of a computer, including how the operating system manages memory and I/O, how compilers generate code, and even how applications use the computer. Of course, because all programs spend much of their time accessing memory, the memory system is necessarily a major factor in determining performance. The reliance on memory hierarchies to achieve performance has meant that programmers, who used to be able to think of memory as a flat, random access storage device, now need to understand that memory is a hierarchy to get good performance. We show how important this understanding is in later examples, such as Figure 5.18 on page 408, and Section 5.14, which shows how to double matrix multiply performance.
Since memory systems are critical to performance, computer designers devote a great deal of attention to these systems and develop sophisticated mechanisms for improving the performance of the memory system. In this chapter, we discuss the major conceptual ideas, although we use many simplifications and abstractions to keep the material manageable in length and complexity.
The BIG Picture
Programs exhibit both temporal locality, the tendency to reuse recently accessed data items, and spatial locality, the tendency to reference data items that are close to other recently accessed items. Memory hierarchies take advantage of temporal locality by keeping more recently accessed data items closer to the processor. Memory hierarchies take advantage of spatial locality by moving blocks consisting of multiple contiguous words in memory to upper levels of the hierarchy.
Figure 5.3 shows that a memory hierarchy uses smaller and faster memory technologies close to the processor. Thus, accesses that hit in the highest level of the hierarchy can be processed quickly. Accesses that miss go to lower levels of the hierarchy, which are larger but slower. If the hit rate is high enough, the memory hierarchy has an effective access time close to that of the highest (and fastest) level and a size equal to that of the lowest (and largest) level.
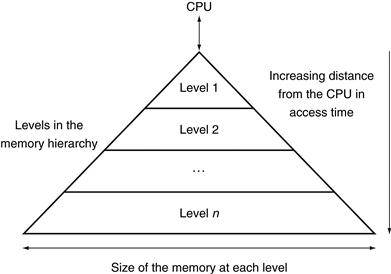
FIGURE 5.3 This diagram shows the structure of a memory hierarchy: as the distance from the processor increases, so does the size.
This structure, with the appropriate operating mechanisms, allows the processor to have an access time that is determined primarily by level 1 of the hierarchy and yet have a memory as large as level n. Maintaining this illusion is the subject of this chapter. Although the local disk is normally the bottom of the hierarchy, some systems use tape or a file server over a local area network as the next levels of the hierarchy.
In most systems, the memory is a true hierarchy, meaning that data cannot be present in level i unless it is also present in level i+1.
Check Yourself
Which of the following statements are generally true?
1. Memory hierarchies take advantage of temporal locality.
2. On a read, the value returned depends on which blocks are in the cache.
3. Most of the cost of the memory hierarchy is at the highest level.
4. Most of the capacity of the memory hierarchy is at the lowest level.
5.2 Memory Technologies
There are four primary technologies used today in memory hierarchies. Main memory is implemented from DRAM (dynamic random access memory), while levels closer to the processor (caches) use SRAM (static random access memory). DRAM is less costly per bit than SRAM, although it is substantially slower. The price difference arises because DRAM uses significantly less area per bit of memory, and DRAMs thus have larger capacity for the same amount of silicon; the speed difference arises from several factors described in Section B.9 of ![]() Appendix B. The third technology is flash memory. This nonvolatile memory is the secondary memory in Personal Mobile Devices. The fourth technology, used to implement the largest and slowest level in the hierarchy in servers, is magnetic disk. The access time and price per bit vary widely among these technologies, as the table below shows, using typical values for 2012:
Appendix B. The third technology is flash memory. This nonvolatile memory is the secondary memory in Personal Mobile Devices. The fourth technology, used to implement the largest and slowest level in the hierarchy in servers, is magnetic disk. The access time and price per bit vary widely among these technologies, as the table below shows, using typical values for 2012:
|
Memory technology |
Typical access time |
$ per GiB in 2012 |
|
SRAM semiconductor memory |
0.5–2.5 ns |
$500–$1000 |
|
DRAM semiconductor memory |
50–70 ns |
$10–$20 |
|
Flash semiconductor memory |
5,000–50,000 ns |
$0.75–$1.00 |
|
Magnetic disk |
5,000,000–20,000,000 ns |
$0.05–$0.10 |
We describe each memory technology in the remainder of this section.
SRAM Technology
SRAMs are simply integrated circuits that are memory arrays with (usually) a single access port that can provide either a read or a write. SRAMs have a fixed access time to any datum, though the read and write access times may differ.
SRAMs don’t need to refresh and so the access time is very close to the cycle time. SRAMs typically use six to eight transistors per bit to prevent the information from being disturbed when read. SRAM needs only minimal power to retain the charge in standby mode.
In the past, most PCs and server systems used separate SRAM chips for either their primary, secondary, or even tertiary caches. Today, thanks to Moore’s Law, all levels of caches are integrated onto the processor chip, so the market for separate SRAM chips has nearly evaporated.

DRAM Technology
In a SRAM, as long as power is applied, the value can be kept indefinitely. In a dynamic RAM (DRAM), the value kept in a cell is stored as a charge in a capacitor. A single transistor is then used to access this stored charge, either to read the value or to overwrite the charge stored there. Because DRAMs use only a single transistor per bit of storage, they are much denser and cheaper per bit than SRAM. As DRAMs store the charge on a capacitor, it cannot be kept indefinitely and must periodically be refreshed. That is why this memory structure is called dynamic, as opposed to the static storage in an SRAM cell.
To refresh the cell, we merely read its contents and write it back. The charge can be kept for several milliseconds. If every bit had to be read out of the DRAM and then written back individually, we would constantly be refreshing the DRAM, leaving no time for accessing it. Fortunately, DRAMs use a two-level decoding structure, and this allows us to refresh an entire row (which shares a word line) with a read cycle followed immediately by a write cycle.
Figure 5.4 shows the internal organization of a DRAM, and Figure 5.5 shows how the density, cost, and access time of DRAMs have changed over the years.
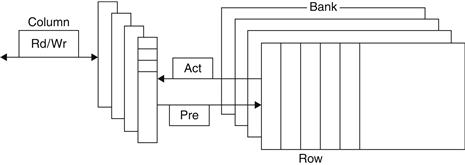
FIGURE 5.4 Internal organization of a DRAM.
Modern DRAMs are organized in banks, typically four for DDR3. Each bank consists of a series of rows. Sending a PRE (precharge) command opens or closes a bank. A row address is sent with an Act (activate), which causes the row to transfer to a buffer. When the row is in the buffer, it can be transferred by successive column addresses at whatever the width of the DRAM is (typically 4, 8, or 16 bits in DDR3) or by specifying a block transfer and the starting address. Each command, as well as block transfers, is synchronized with a clock.
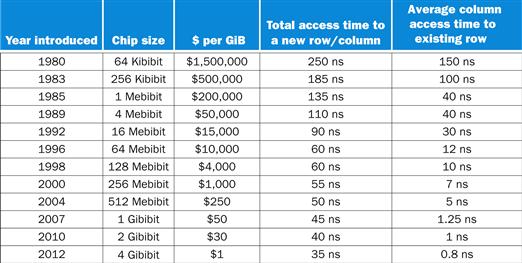
FIGURE 5.5 DRAM size increased by multiples of four approximately once every three years until 1996, and thereafter considerably slower.
The improvements in access time have been slower but continuous, and cost roughly tracks density improvements, although cost is often affected by other issues, such as availability and demand. The cost per gibibyte is not adjusted for inflation.
The row organization that helps with refresh also helps with performance. To improve performance, DRAMs buffer rows for repeated access. The buffer acts like an SRAM; by changing the address, random bits can be accessed in the buffer until the next row access. This capability improves the access time significantly, since the access time to bits in the row is much lower. Making the chip wider also improves the memory bandwidth of the chip. When the row is in the buffer, it can be transferred by successive addresses at whatever the width of the DRAM is (typically 4, 8, or 16 bits), or by specifying a block transfer and the starting address within the buffer.
To further improve the interface to processors, DRAMs added clocks and are properly called Synchronous DRAMs or SDRAMs. The advantage of SDRAMs is that the use of a clock eliminates the time for the memory and processor to synchronize. The speed advantage of synchronous DRAMs comes from the ability to transfer the bits in the burst without having to specify additional address bits. Instead, the clock transfers the successive bits in a burst. The fastest version is called Double Data Rate (DDR) SDRAM. The name means data transfers on both the rising and falling edge of the clock, thereby getting twice as much bandwidth as you might expect based on the clock rate and the data width. The latest version of this technology is called DDR4. A DDR4-3200 DRAM can do 3200 million transfers per second, which means it has a 1600 MHz clock.
Sustaining that much bandwidth requires clever organization inside the DRAM. Instead of just a faster row buffer, the DRAM can be internally organized to read or write from multiple banks, with each having its own row buffer. Sending an address to several banks permits them all to read or write simultaneously. For example, with four banks, there is just one access time and then accesses rotate between the four banks to supply four times the bandwidth. This rotating access scheme is called address interleaving.
Although Personal Mobile Devices like the iPad (see Chapter 1) use individual DRAMs, memory for servers are commonly sold on small boards called dual inline memory modules (DIMMs). DIMMs typically contain 4–16 DRAMs, and they are normally organized to be 8 bytes wide for server systems. A DIMM using DDR4-3200 SDRAMs could transfer at 8×3200=25,600 megabytes per second. Such DIMMs are named after their bandwidth: PC25600. Since a DIMM can have so many DRAM chips that only a portion of them are used for a particular transfer, we need a term to refer to the subset of chips in a DIMM that share common address lines. To avoid confusion with the internal DRAM names of row and banks, we use the term memory rank for such a subset of chips in a DIMM.
Elaboration
One way to measure the performance of the memory system behind the caches is the Stream benchmark [McCalpin, 1995]. It measures the performance of long vector operations. They have no temporal locality and they access arrays that are larger than the cache of the computer being tested.
Flash Memory
Flash memory is a type of electrically erasable programmable read-only memory (EEPROM).
Unlike disks and DRAM, but like other EEPROM technologies, writes can wear out flash memory bits. To cope with such limits, most flash products include a controller to spread the writes by remapping blocks that have been written many times to less trodden blocks. This technique is called wear leveling. With wear leveling, personal mobile devices are very unlikely to exceed the write limits in the flash. Such wear leveling lowers the potential performance of flash, but it is needed unless higher-level software monitors block wear. Flash controllers that perform wear leveling can also improve yield by mapping out memory cells that were manufactured incorrectly.
Disk Memory
As Figure 5.6 shows, a magnetic hard disk consists of a collection of platters, which rotate on a spindle at 5400 to 15,000 revolutions per minute. The metal platters are covered with magnetic recording material on both sides, similar to the material found on a cassette or videotape. To read and write information on a hard disk, a movable arm containing a small electromagnetic coil called a read-write head is located just above each surface. The entire drive is permanently sealed to control the environment inside the drive, which, in turn, allows the disk heads to be much closer to the drive surface.

FIGURE 5.6 A disk showing 10 disk platters and the read/write heads.
The diameter of today’s disks is 2.5 or 3.5 inches, and there are typically one or two platters per drive today.
Each disk surface is divided into concentric circles, called tracks. There are typically tens of thousands of tracks per surface. Each track is in turn divided into sectors that contain the information; each track may have thousands of sectors. Sectors are typically 512 to 4096 bytes in size. The sequence recorded on the magnetic media is a sector number, a gap, the information for that sector including error correction code (see Section 5.5), a gap, the sector number of the next sector, and so on.
track
One of thousands of concentric circles that makes up the surface of a magnetic disk.
sector
One of the segments that make up a track on a magnetic disk; a sector is the smallest amount of information that is read or written on a disk.
The disk heads for each surface are connected together and move in conjunction, so that every head is over the same track of every surface. The term cylinder is used to refer to all the tracks under the heads at a given point on all surfaces.
To access data, the operating system must direct the disk through a three-stage process. The first step is to position the head over the proper track. This operation is called a seek, and the time to move the head to the desired track is called the seek time.
seek
The process of positioning a read/write head over the proper track on a disk.
Disk manufacturers report minimum seek time, maximum seek time, and average seek time in their manuals. The first two are easy to measure, but the average is open to wide interpretation because it depends on the seek distance. The industry calculates average seek time as the sum of the time for all possible seeks divided by the number of possible seeks. Average seek times are usually advertised as 3 ms to 13 ms, but, depending on the application and scheduling of disk requests, the actual average seek time may be only 25% to 33% of the advertised number because of locality of disk references. This locality arises both because of successive accesses to the same file and because the operating system tries to schedule such accesses together.
Once the head has reached the correct track, we must wait for the desired sector to rotate under the read/write head. This time is called the rotational latency or rotational delay. The average latency to the desired information is halfway around the disk. Disks rotate at 5400 RPM to 15,000 RPM. The average rotational latency at 5400 RPM is
rotational latency
Also called rotational delay. The time required for the desired sector of a disk to rotate under the read/write head; usually assumed to be half the rotation time.

The last component of a disk access, transfer time, is the time to transfer a block of bits. The transfer time is a function of the sector size, the rotation speed, and the recording density of a track. Transfer rates in 2012 were between 100 and 200 MB/sec.
One complication is that most disk controllers have a built-in cache that stores sectors as they are passed over; transfer rates from the cache are typically higher, and were up to 750 MB/sec (6 Gbit/sec) in 2012.
Alas, where block numbers are located is no longer intuitive. The assumptions of the sector-track-cylinder model above are that nearby blocks are on the same track, blocks in the same cylinder take less time to access since there is no seek time, and some tracks are closer than others. The reason for the change was the raising of the level of the disk interfaces. To speed-up sequential transfers, these higher-level interfaces organize disks more like tapes than like random access devices. The logical blocks are ordered in serpentine fashion across a single surface, trying to capture all the sectors that are recorded at the same bit density to try to get best performance. Hence, sequential blocks may be on different tracks.
In summary, the two primary differences between magnetic disks and semiconductor memory technologies are that disks have a slower access time because they are mechanical devices—flash is 1000 times as fast and DRAM is 100,000 times as fast—yet they are cheaper per bit because they have very high storage capacity at a modest cost—disk is 10 to 100 time cheaper. Magnetic disks are nonvolatile like flash, but unlike flash there is no write wear-out problem. However, flash is much more rugged and hence a better match to the jostling inherent in personal mobile devices.
5.3 The Basics of Caches
Cache: a safe place for hiding or storing things.
Webster’s New World Dictionary of the American Language, Third College Edition, 1988
In our library example, the desk acted as a cache—a safe place to store things (books) that we needed to examine. Cache was the name chosen to represent the level of the memory hierarchy between the processor and main memory in the first commercial computer to have this extra level. The memories in the datapath in Chapter 4 are simply replaced by caches. Today, although this remains the dominant use of the word cache, the term is also used to refer to any storage managed to take advantage of locality of access. Caches first appeared in research computers in the early 1960s and in production computers later in that same decade; every general-purpose computer built today, from servers to low-power embedded processors, includes caches.
In this section, we begin by looking at a very simple cache in which the processor requests are each one word and the blocks also consist of a single word. (Readers already familiar with cache basics may want to skip to Section 5.4.) Figure 5.7 shows such a simple cache, before and after requesting a data item that is not initially in the cache. Before the request, the cache contains a collection of recent references X1, X2, …, Xn−1, and the processor requests a word Xn that is not in the cache. This request results in a miss, and the word Xn is brought from memory into the cache.

FIGURE 5.7 The cache just before and just after a reference to a word Xn that is not initially in the cache.
This reference causes a miss that forces the cache to fetch Xn from memory and insert it into the cache.
In looking at the scenario in Figure 5.7, there are two questions to answer: How do we know if a data item is in the cache? Moreover, if it is, how do we find it? The answers are related. If each word can go in exactly one place in the cache, then it is straightforward to find the word if it is in the cache. The simplest way to assign a location in the cache for each word in memory is to assign the cache location based on the address of the word in memory. This cache structure is called direct mapped, since each memory location is mapped directly to exactly one location in the cache. The typical mapping between addresses and cache locations for a direct-mapped cache is usually simple. For example, almost all direct-mapped caches use this mapping to find a block:
![]()
direct-mapped cache
A cache structure in which each memory location is mapped to exactly one location in the cache.
If the number of entries in the cache is a power of 2, then modulo can be computed simply by using the low-order log2 (cache size in blocks) bits of the address. Thus, an 8-block cache uses the three lowest bits (8=23) of the block address. For example, Figure 5.8 shows how the memory addresses between 1ten (00001two) and 29ten (11101two) map to locations 1ten (001two) and 5ten (101two) in a direct-mapped cache of eight words.
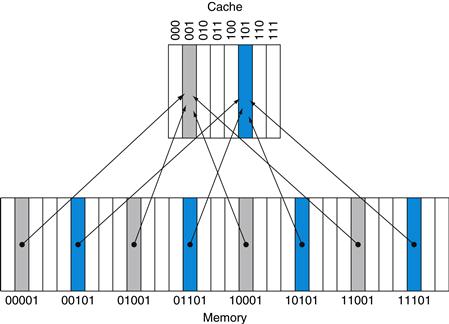
FIGURE 5.8 A direct-mapped cache with eight entries showing the addresses of memory words between 0 and 31 that map to the same cache locations.
Because there are eight words in the cache, an address X maps to the direct-mapped cache word X modulo 8. That is, the low-order log2(8)=3 bits are used as the cache index. Thus, addresses 00001two, 01001two, 10001two, and 11001two all map to entry 001two of the cache, while addresses 00101two, 01101two, 10101two, and 11101two all map to entry 101two of the cache.
Because each cache location can contain the contents of a number of different memory locations, how do we know whether the data in the cache corresponds to a requested word? That is, how do we know whether a requested word is in the cache or not? We answer this question by adding a set of tags to the cache. The tags contain the address information required to identify whether a word in the cache corresponds to the requested word. The tag needs only to contain the upper portion of the address, corresponding to the bits that are not used as an index into the cache. For example, in Figure 5.8 we need only have the upper 2 of the 5 address bits in the tag, since the lower 3-bit index field of the address selects the block. Architects omit the index bits because they are redundant, since by definition the index field of any address of a cache block must be that block number.
tag
A field in a table used for a memory hierarchy that contains the address information required to identify whether the associated block in the hierarchy corresponds to a requested word.
We also need a way to recognize that a cache block does not have valid information. For instance, when a processor starts up, the cache does not have good data, and the tag fields will be meaningless. Even after executing many instructions, some of the cache entries may still be empty, as in Figure 5.7. Thus, we need to know that the tag should be ignored for such entries. The most common method is to add a valid bit to indicate whether an entry contains a valid address. If the bit is not set, there cannot be a match for this block.
valid bit
A field in the tables of a memory hierarchy that indicates that the associated block in the hierarchy contains valid data.
For the rest of this section, we will focus on explaining how a cache deals with reads. In general, handling reads is a little simpler than handling writes, since reads do not have to change the contents of the cache. After seeing the basics of how reads work and how cache misses can be handled, we’ll examine the cache designs for real computers and detail how these caches handle writes.
The BIG Picture
Caching is perhaps the most important example of the big idea of prediction. It relies on the principle of locality to try to find the desired data in the higher levels of the memory hierarchy, and provides mechanisms to ensure that when the prediction is wrong it finds and uses the proper data from the lower levels of the memory hierarchy. The hit rates of the cache prediction on modern computers are often higher than 95% (see Figure 5.47).

Accessing a Cache
Below is a sequence of nine memory references to an empty eight-block cache, including the action for each reference. Figure 5.9 shows how the contents of the cache change on each miss. Since there are eight blocks in the cache, the low-order three bits of an address give the block number:
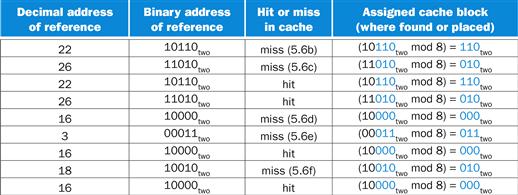
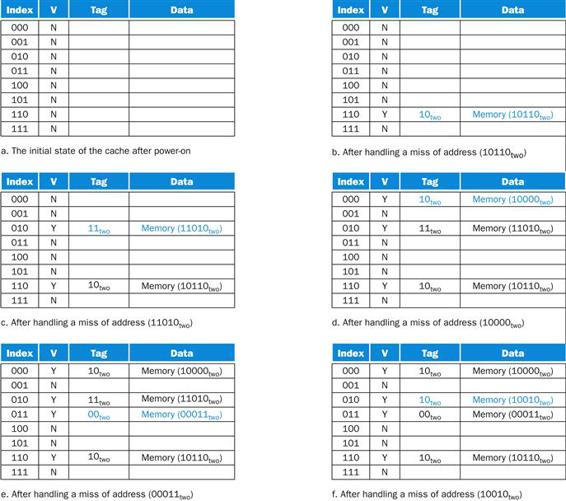
FIGURE 5.9 The cache contents are shown after each reference request that misses, with the index and tag fields shown in binary for the sequence of addresses on page 386.
The cache is initially empty, with all valid bits (V entry in cache) turned off (N). The processor requests the following addresses: 10110two (miss), 11010two (miss), 10110two (hit), 11010two (hit), 10000two (miss), 00011two (miss), 10000two (hit), 10010two (miss), and 10000two(hit). The figures show the cache contents after each miss in the sequence has been handled. When address 10010two (18) is referenced, the entry for address 11010two (26) must be replaced, and a reference to 11010two will cause a subsequent miss. The tag field will contain only the upper portion of the address. The full address of a word contained in cache block i with tag field j for this cache is j×8+i, or equivalently the concatenation of the tag field j and the index i. For example, in cache f above, index 010two has tag 10two and corresponds to address 10010two.
Since the cache is empty, several of the first references are misses; the caption of Figure 5.9 describes the actions for each memory reference. On the eighth reference we have conflicting demands for a block. The word at address 18 (10010two) should be brought into cache block 2 (010two). Hence, it must replace the word at address 26 (11010two), which is already in cache block 2 (010two). This behavior allows a cache to take advantage of temporal locality: recently referenced words replace less recently referenced words.
This situation is directly analogous to needing a book from the shelves and having no more space on your desk—some book already on your desk must be returned to the shelves. In a direct-mapped cache, there is only one place to put the newly requested item and hence only one choice of what to replace.
We know where to look in the cache for each possible address: the low-order bits of an address can be used to find the unique cache entry to which the address could map. Figure 5.10 shows how a referenced address is divided into
■ A tag field, which is used to compare with the value of the tag field of the cache
■ A cache index, which is used to select the block
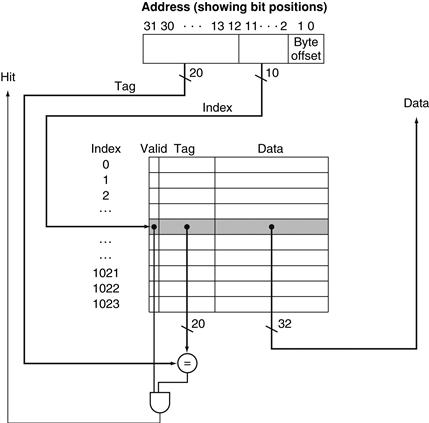
FIGURE 5.10 For this cache, the lower portion of the address is used to select a cache entry consisting of a data word and a tag.
This cache holds 1024 words or 4 KiB. We assume 32-bit addresses in this chapter. The tag from the cache is compared against the upper portion of the address to determine whether the entry in the cache corresponds to the requested address. Because the cache has 210 (or 1024) words and a block size of one word, 10 bits are used to index the cache, leaving 32−10−2=20 bits to be compared against the tag. If the tag and upper 20 bits of the address are equal and the valid bit is on, then the request hits in the cache, and the word is supplied to the processor. Otherwise, a miss occurs.
The index of a cache block, together with the tag contents of that block, uniquely specifies the memory address of the word contained in the cache block. Because the index field is used as an address to reference the cache, and because an n-bit field has 2n values, the total number of entries in a direct-mapped cache must be a power of 2. In the MIPS architecture, since words are aligned to multiples of four bytes, the least significant two bits of every address specify a byte within a word. Hence, the least significant two bits are ignored when selecting a word in the block.
The total number of bits needed for a cache is a function of the cache size and the address size, because the cache includes both the storage for the data and the tags. The size of the block above was one word, but normally it is several. For the following situation:
■ 32-bit addresses
■ A direct-mapped cache
■ The cache size is 2n blocks, so n bits are used for the index
■ The block size is 2m words (2m+2 bytes), so m bits are used for the word within the block, and two bits are used for the byte part of the address
the size of the tag field is
![]()
The total number of bits in a direct-mapped cache is
![]()
Since the block size is 2m words (2m+5 bits), and we need 1 bit for the valid field, the number of bits in such a cache is
![]()
Although this is the actual size in bits, the naming convention is to exclude the size of the tag and valid field and to count only the size of the data. Thus, the cache in Figure 5.10 is called a 4 KiB cache.
Bits in a Cache
Example
How many total bits are required for a direct-mapped cache with 16 KiB of data and 4-word blocks, assuming a 32-bit address?
Answer
We know that 16 KiB is 4096 (212) words. With a block size of 4 words (22), there are 1024 (210) blocks. Each block has 4×32 or 128 bits of data plus a tag, which is 32−10−2−2 bits, plus a valid bit. Thus, the total cache size is
![]()
or 18.4 KiB for a 16 KiB cache. For this cache, the total number of bits in the cache is about 1.15 times as many as needed just for the storage of the data.
Mapping an Address to a Multiword Cache Block
Example
Consider a cache with 64 blocks and a block size of 16 bytes. To what block number does byte address 1200 map?
Answer
We saw the formula on page 384. The block is given by
![]()
where the address of the block is
![]()
Notice that this block address is the block containing all addresses between
![]()
and
![]()
Thus, with 16 bytes per block, byte address 1200 is block address
![]()
which maps to cache block number (75 modulo 64)=11. In fact, this block maps all addresses between 1200 and 1215.
Larger blocks exploit spatial locality to lower miss rates. As Figure 5.11 shows, increasing the block size usually decreases the miss rate. The miss rate may go up eventually if the block size becomes a significant fraction of the cache size, because the number of blocks that can be held in the cache will become small, and there will be a great deal of competition for those blocks. As a result, a block will be bumped out of the cache before many of its words are accessed. Stated alternatively, spatial locality among the words in a block decreases with a very large block; consequently, the benefits in the miss rate become smaller.
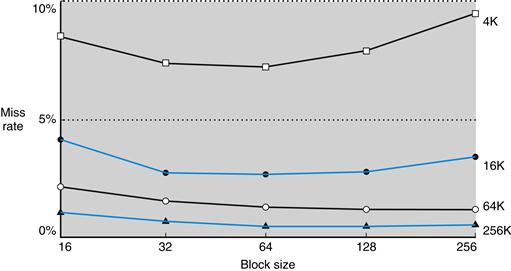
FIGURE 5.11 Miss rate versus block size.
Note that the miss rate actually goes up if the block size is too large relative to the cache size. Each line represents a cache of different size. (This figure is independent of associativity, discussed soon.) Unfortunately, SPEC CPU2000 traces would take too long if block size were included, so this data is based on SPEC92.
A more serious problem associated with just increasing the block size is that the cost of a miss increases. The miss penalty is determined by the time required to fetch the block from the next lower level of the hierarchy and load it into the cache. The time to fetch the block has two parts: the latency to the first word and the transfer time for the rest of the block. Clearly, unless we change the memory system, the transfer time—and hence the miss penalty—will likely increase as the block size increases. Furthermore, the improvement in the miss rate starts to decrease as the blocks become larger. The result is that the increase in the miss penalty overwhelms the decrease in the miss rate for blocks that are too large, and cache performance thus decreases. Of course, if we design the memory to transfer larger blocks more efficiently, we can increase the block size and obtain further improvements in cache performance. We discuss this topic in the next section.
Elaboration
Although it is hard to do anything about the longer latency component of the miss penalty for large blocks, we may be able to hide some of the transfer time so that the miss penalty is effectively smaller. The simplest method for doing this, called early restart, is simply to resume execution as soon as the requested word of the block is returned, rather than wait for the entire block. Many processors use this technique for instruction access, where it works best. Instruction accesses are largely sequential, so if the memory system can deliver a word every clock cycle, the processor may be able to restart operation when the requested word is returned, with the memory system delivering new instruction words just in time. This technique is usually less effective for data caches because it is likely that the words will be requested from the block in a less predictable way, and the probability that the processor will need another word from a different cache block before the transfer completes is high. If the processor cannot access the data cache because a transfer is ongoing, then it must stall.
An even more sophisticated scheme is to organize the memory so that the requested word is transferred from the memory to the cache first. The remainder of the block is then transferred, starting with the address after the requested word and wrapping around to the beginning of the block. This technique, called requested word first or critical word first, can be slightly faster than early restart, but it is limited by the same properties that limit early restart.
Handling Cache Misses
Before we look at the cache of a real system, let’s see how the control unit deals with cache misses. (We describe a cache controller in detail in Section 5.9). The control unit must detect a miss and process the miss by fetching the requested data from memory (or, as we shall see, a lower-level cache). If the cache reports a hit, the computer continues using the data as if nothing happened.
cache miss
A request for data from the cache that cannot be filled because the data is not present in the cache.
Modifying the control of a processor to handle a hit is trivial; misses, however, require some extra work. The cache miss handling is done in collaboration with the processor control unit and with a separate controller that initiates the memory access and refills the cache. The processing of a cache miss creates a pipeline stall (Chapter 4) as opposed to an interrupt, which would require saving the state of all registers. For a cache miss, we can stall the entire processor, essentially freezing the contents of the temporary and programmer-visible registers, while we wait for memory. More sophisticated out-of-order processors can allow execution of instructions while waiting for a cache miss, but we’ll assume in-order processors that stall on cache misses in this section.
Let’s look a little more closely at how instruction misses are handled; the same approach can be easily extended to handle data misses. If an instruction access results in a miss, then the content of the Instruction register is invalid. To get the proper instruction into the cache, we must be able to instruct the lower level in the memory hierarchy to perform a read. Since the program counter is incremented in the first clock cycle of execution, the address of the instruction that generates an instruction cache miss is equal to the value of the program counter minus 4. Once we have the address, we need to instruct the main memory to perform a read. We wait for the memory to respond (since the access will take multiple clock cycles), and then write the words containing the desired instruction into the cache.
We can now define the steps to be taken on an instruction cache miss:
1. Send the original PC value (current PC – 4) to the memory.
2. Instruct main memory to perform a read and wait for the memory to complete its access.
3. Write the cache entry, putting the data from memory in the data portion of the entry, writing the upper bits of the address (from the ALU) into the tag field, and turning the valid bit on.
4. Restart the instruction execution at the first step, which will refetch the instruction, this time finding it in the cache.
The control of the cache on a data access is essentially identical: on a miss, we simply stall the processor until the memory responds with the data.
Handling Writes
Writes work somewhat differently. Suppose on a store instruction, we wrote the data into only the data cache (without changing main memory); then, after the write into the cache, memory would have a different value from that in the cache. In such a case, the cache and memory are said to be inconsistent. The simplest way to keep the main memory and the cache consistent is always to write the data into both the memory and the cache. This scheme is called write-through.
write-through
A scheme in which writes always update both the cache and the next lower level of the memory hierarchy, ensuring that data is always consistent between the two.
The other key aspect of writes is what occurs on a write miss. We first fetch the words of the block from memory. After the block is fetched and placed into the cache, we can overwrite the word that caused the miss into the cache block. We also write the word to main memory using the full address.
Although this design handles writes very simply, it would not provide very good performance. With a write-through scheme, every write causes the data to be written to main memory. These writes will take a long time, likely at least 100 processor clock cycles, and could slow down the processor considerably. For example, suppose 10% of the instructions are stores. If the CPI without cache misses was 1.0, spending 100 extra cycles on every write would lead to a CPI of 1.0+100×10%=11, reducing performance by more than a factor of 10.
One solution to this problem is to use a write buffer. A write buffer stores the data while it is waiting to be written to memory. After writing the data into the cache and into the write buffer, the processor can continue execution. When a write to main memory completes, the entry in the write buffer is freed. If the write buffer is full when the processor reaches a write, the processor must stall until there is an empty position in the write buffer. Of course, if the rate at which the memory can complete writes is less than the rate at which the processor is generating writes, no amount of buffering can help, because writes are being generated faster than the memory system can accept them.
write buffer
A queue that holds data while the data is waiting to be written to memory.
The rate at which writes are generated may also be less than the rate at which the memory can accept them, and yet stalls may still occur. This can happen when the writes occur in bursts. To reduce the occurrence of such stalls, processors usually increase the depth of the write buffer beyond a single entry.
The alternative to a write-through scheme is a scheme called write-back. In a write-back scheme, when a write occurs, the new value is written only to the block in the cache. The modified block is written to the lower level of the hierarchy when it is replaced. Write-back schemes can improve performance, especially when processors can generate writes as fast or faster than the writes can be handled by main memory; a write-back scheme is, however, more complex to implement than write-through.
write-back
A scheme that handles writes by updating values only to the block in the cache, then writing the modified block to the lower level of the hierarchy when the block is replaced.
In the rest of this section, we describe caches from real processors, and we examine how they handle both reads and writes. In Section 5.8, we will describe the handling of writes in more detail.
Elaboration
Writes introduce several complications into caches that are not present for reads. Here we discuss two of them: the policy on write misses and efficient implementation of writes in write-back caches.
Consider a miss in a write-through cache. The most common strategy is to allocate a block in the cache, called write allocate. The block is fetched from memory and then the appropriate portion of the block is overwritten. An alternative strategy is to update the portion of the block in memory but not put it in the cache, called no write allocate. The motivation is that sometimes programs write entire blocks of data, such as when the operating system zeros a page of memory. In such cases, the fetch associated with the initial write miss may be unnecessary. Some computers allow the write allocation policy to be changed on a per page basis.
Actually implementing stores efficiently in a cache that uses a write-back strategy is more complex than in a write-through cache. A write-through cache can write the data into the cache and read the tag; if the tag mismatches, then a miss occurs. Because the cache is write-through, the overwriting of the block in the cache is not catastrophic, since memory has the correct value. In a write-back cache, we must first write the block back to memory if the data in the cache is modified and we have a cache miss. If we simply overwrote the block on a store instruction before we knew whether the store had hit in the cache (as we could for a write-through cache), we would destroy the contents of the block, which is not backed up in the next lower level of the memory hierarchy.
In a write-back cache, because we cannot overwrite the block, stores either require two cycles (a cycle to check for a hit followed by a cycle to actually perform the write) or require a write buffer to hold that data—effectively allowing the store to take only one cycle by pipelining it. When a store buffer is used, the processor does the cache lookup and places the data in the store buffer during the normal cache access cycle. Assuming a cache hit, the new data is written from the store buffer into the cache on the next unused cache access cycle.
By comparison, in a write-through cache, writes can always be done in one cycle. We read the tag and write the data portion of the selected block. If the tag matches the address of the block being written, the processor can continue normally, since the correct block has been updated. If the tag does not match, the processor generates a write miss to fetch the rest of the block corresponding to that address.
Many write-back caches also include write buffers that are used to reduce the miss penalty when a miss replaces a modified block. In such a case, the modified block is moved to a write-back buffer associated with the cache while the requested block is read from memory. The write-back buffer is later written back to memory. Assuming another miss does not occur immediately, this technique halves the miss penalty when a dirty block must be replaced.
An Example Cache: The Intrinsity FastMATH Processor
The Intrinsity FastMATH is an embedded microprocessor that uses the MIPS architecture and a simple cache implementation. Near the end of the chapter, we will examine the more complex cache designs of ARM and Intel microprocessors, but we start with this simple, yet real, example for pedagogical reasons. Figure 5.12 shows the organization of the Intrinsity FastMATH data cache.
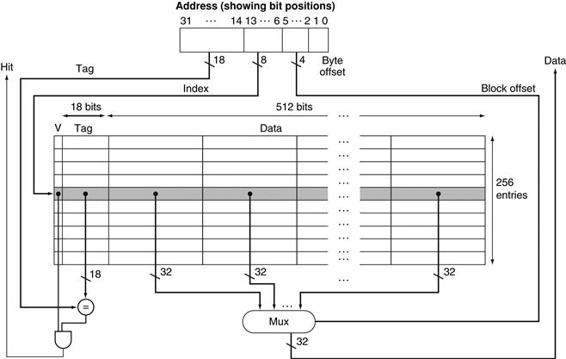
FIGURE 5.12 The 16 KiB caches in the Intrinsity FastMATH each contain 256 blocks with 16 words per block.
The tag field is 18 bits wide and the index field is 8 bits wide, while a 4-bit field (bits 5–2) is used to index the block and select the word from the block using a 16-to-1 multiplexor. In practice, to eliminate the multiplexor, caches use a separate large RAM for the data and a smaller RAM for the tags, with the block offset supplying the extra address bits for the large data RAM. In this case, the large RAM is 32 bits wide and must have 16 times as many words as blocks in the cache.
This processor has a 12-stage pipeline. When operating at peak speed, the processor can request both an instruction word and a data word on every clock. To satisfy the demands of the pipeline without stalling, separate instruction and data caches are used. Each cache is 16 KiB, or 4096 words, with 16-word blocks.
Read requests for the cache are straightforward. Because there are separate data and instruction caches, we need separate control signals to read and write each cache. (Remember that we need to update the instruction cache when a miss occurs.) Thus, the steps for a read request to either cache are as follows:
1. Send the address to the appropriate cache. The address comes either from the PC (for an instruction) or from the ALU (for data).
2. If the cache signals hit, the requested word is available on the data lines. Since there are 16 words in the desired block, we need to select the right one. A block index field is used to control the multiplexor (shown at the bottom of the figure), which selects the requested word from the 16 words in the indexed block.
3. If the cache signals miss, we send the address to the main memory. When the memory returns with the data, we write it into the cache and then read it to fulfill the request.
For writes, the Intrinsity FastMATH offers both write-through and write-back, leaving it up to the operating system to decide which strategy to use for an application. It has a one-entry write buffer.
What cache miss rates are attained with a cache structure like that used by the Intrinsity FastMATH? Figure 5.13 shows the miss rates for the instruction and data caches. The combined miss rate is the effective miss rate per reference for each program after accounting for the differing frequency of instruction and data accesses.
![]()
FIGURE 5.13 Approximate instruction and data miss rates for the Intrinsity FastMATH processor for SPEC CPU2000 benchmarks.
The combined miss rate is the effective miss rate seen for the combination of the 16 KiB instruction cache and 16 KiB data cache. It is obtained by weighting the instruction and data individual miss rates by the frequency of instruction and data references.
Although miss rate is an important characteristic of cache designs, the ultimate measure will be the effect of the memory system on program execution time; we’ll see how miss rate and execution time are related shortly.
Elaboration
A combined cache with a total size equal to the sum of the two split caches will usually have a better hit rate. This higher rate occurs because the combined cache does not rigidly divide the number of entries that may be used by instructions from those that may be used by data. Nonetheless, almost all processors today use split instruction and data caches to increase cache bandwidthto match what modern pipelines expect. (There may also be fewer conflict misses; see Section 5.8.)
split cache
A scheme in which a level of the memory hierarchy is composed of two independent caches that operate in parallel with each other, with one handling instructions and one handling data.
Here are miss rates for caches the size of those found in the Intrinsity FastMATH processor, and for a combined cache whose size is equal to the sum of the two caches:
■ Total cache size: 32 KiB
■ Split cache effective miss rate: 3.24%
■ Combined cache miss rate: 3.18%
The miss rate of the split cache is only slightly worse.
The advantage of doubling the cache bandwidth, by supporting both an instruction and data access simultaneously, easily overcomes the disadvantage of a slightly increased miss rate. This observation cautions us that we cannot use miss rate as the sole measure of cache performance, as Section 5.4 shows.
Summary
We began the previous section by examining the simplest of caches: a direct-mapped cache with a one-word block. In such a cache, both hits and misses are simple, since a word can go in exactly one location and there is a separate tag for every word. To keep the cache and memory consistent, a write-through scheme can be used, so that every write into the cache also causes memory to be updated. The alternative to write-through is a write-back scheme that copies a block back to memory when it is replaced; we’ll discuss this scheme further in upcoming sections.
To take advantage of spatial locality, a cache must have a block size larger than one word. The use of a larger block decreases the miss rate and improves the efficiency of the cache by reducing the amount of tag storage relative to the amount of data storage in the cache. Although a larger block size decreases the miss rate, it can also increase the miss penalty. If the miss penalty increased linearly with the block size, larger blocks could easily lead to lower performance.
To avoid performance loss, the bandwidth of main memory is increased to transfer cache blocks more efficiently. Common methods for increasing bandwidth external to the DRAM are making the memory wider and interleaving. DRAM designers have steadily improved the interface between the processor and memory to increase the bandwidth of burst mode transfers to reduce the cost of larger cache block sizes.
Check Yourself
The speed of the memory system affects the designer’s decision on the size of the cache block. Which of the following cache designer guidelines are generally valid?
1. The shorter the memory latency, the smaller the cache block
2. The shorter the memory latency, the larger the cache block
3. The higher the memory bandwidth, the smaller the cache block
4. The higher the memory bandwidth, the larger the cache block
5.4 Measuring and Improving Cache Performance
In this section, we begin by examining ways to measure and analyze cache performance. We then explore two different techniques for improving cache performance. One focuses on reducing the miss rate by reducing the probability that two different memory blocks will contend for the same cache location. The second technique reduces the miss penalty by adding an additional level to the hierarchy. This technique, called multilevel caching, first appeared in high-end computers selling for more than $100,000 in 1990; since then it has become common on personal mobile devices selling for a few hundred dollars!
CPU time can be divided into the clock cycles that the CPU spends executing the program and the clock cycles that the CPU spends waiting for the memory system. Normally, we assume that the costs of cache accesses that are hits are part of the normal CPU execution cycles. Thus,
![]()
The memory-stall clock cycles come primarily from cache misses, and we make that assumption here. We also restrict the discussion to a simplified model of the memory system. In real processors, the stalls generated by reads and writes can be quite complex, and accurate performance prediction usually requires very detailed simulations of the processor and memory system.
Memory-stall clock cycles can be defined as the sum of the stall cycles coming from reads plus those coming from writes:
![]()
The read-stall cycles can be defined in terms of the number of read accesses per program, the miss penalty in clock cycles for a read, and the read miss rate:
![]()
Writes are more complicated. For a write-through scheme, we have two sources of stalls: write misses, which usually require that we fetch the block before continuing the write (see the Elaboration on page 394 for more details on dealing with writes), and write buffer stalls, which occur when the write buffer is full when a write occurs. Thus, the cycles stalled for writes equals the sum of these two:
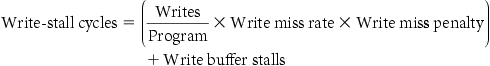
Because the write buffer stalls depend on the proximity of writes, and not just the frequency, it is not possible to give a simple equation to compute such stalls. Fortunately, in systems with a reasonable write buffer depth (e.g., four or more words) and a memory capable of accepting writes at a rate that significantly exceeds the average write frequency in programs (e.g., by a factor of 2), the write buffer stalls will be small, and we can safely ignore them. If a system did not meet these criteria, it would not be well designed; instead, the designer should have used either a deeper write buffer or a write-back organization.
Write-back schemes also have potential additional stalls arising from the need to write a cache block back to memory when the block is replaced. We will discuss this more in Section 5.8.
In most write-through cache organizations, the read and write miss penalties are the same (the time to fetch the block from memory). If we assume that the write buffer stalls are negligible, we can combine the reads and writes by using a single miss rate and the miss penalty:
![]()
We can also factor this as
![]()
Let’s consider a simple example to help us understand the impact of cache performance on processor performance.
Calculating Cache Performance
Example
Assume the miss rate of an instruction cache is 2% and the miss rate of the data cache is 4%. If a processor has a CPI of 2 without any memory stalls and the miss penalty is 100 cycles for all misses, determine how much faster a processor would run with a perfect cache that never missed. Assume the frequency of all loads and stores is 36%.
Answer
The number of memory miss cycles for instructions in terms of the Instruction count (I) is
![]()
As the frequency of all loads and stores is 36%, we can find the number of memory miss cycles for data references:
![]()
The total number of memory-stall cycles is 2.00 I+1.44 I=3.44 I. This is more than three cycles of memory stall per instruction. Accordingly, the total CPI including memory stalls is 2+3.44=5.44. Since there is no change in instruction count or clock rate, the ratio of the CPU execution times is
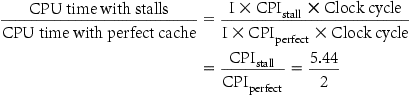
The performance with the perfect cache is better by![]() .
.
What happens if the processor is made faster, but the memory system is not? The amount of time spent on memory stalls will take up an increasing fraction of the execution time; Amdahl’s Law, which we examined in Chapter 1, reminds us of this fact. A few simple examples show how serious this problem can be. Suppose we speed-up the computer in the previous example by reducing its CPI from 2 to 1 without changing the clock rate, which might be done with an improved pipeline. The system with cache misses would then have a CPI of 1+3.44=4.44, and the system with the perfect cache would be
![]()
The amount of execution time spent on memory stalls would have risen from
![]()
to
![]()
Similarly, increasing the clock rate without changing the memory system also increases the performance lost due to cache misses.
The previous examples and equations assume that the hit time is not a factor in determining cache performance. Clearly, if the hit time increases, the total time to access a word from the memory system will increase, possibly causing an increase in the processor cycle time. Although we will see additional examples of what can increase hit time shortly, one example is increasing the cache size. A larger cache could clearly have a longer access time, just as, if your desk in the library was very large (say, 3 square meters), it would take longer to locate a book on the desk. An increase in hit time likely adds another stage to the pipeline, since it may take multiple cycles for a cache hit. Although it is more complex to calculate the performance impact of a deeper pipeline, at some point the increase in hit time for a larger cache could dominate the improvement in hit rate, leading to a decrease in processor performance.
To capture the fact that the time to access data for both hits and misses affects performance, designers sometime use average memory access time (AMAT) as a way to examine alternative cache designs. Average memory access time is the average time to access memory considering both hits and misses and the frequency of different accesses; it is equal to the following:
![]()
Calculating Average Memory Access Time
Example
Find the AMAT for a processor with a 1 ns clock cycle time, a miss penalty of 20 clock cycles, a miss rate of 0.05 misses per instruction, and a cache access time (including hit detection) of 1 clock cycle. Assume that the read and write miss penalties are the same and ignore other write stalls.
Answer
The average memory access time per instruction is
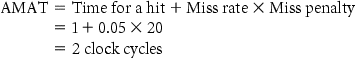
or 2 ns.
The next subsection discusses alternative cache organizations that decrease miss rate but may sometimes increase hit time; additional examples appear in Section 5.15, Fallacies and Pitfalls.
Reducing Cache Misses by More Flexible Placement of Blocks
So far, when we place a block in the cache, we have used a simple placement scheme: A block can go in exactly one place in the cache. As mentioned earlier, it is called direct mapped because there is a direct mapping from any block address in memory to a single location in the upper level of the hierarchy. However, there is actually a whole range of schemes for placing blocks. Direct mapped, where a block can be placed in exactly one location, is at one extreme.
At the other extreme is a scheme where a block can be placed in any location in the cache. Such a scheme is called fully associative, because a block in memory may be associated with any entry in the cache. To find a given block in a fully associative cache, all the entries in the cache must be searched because a block can be placed in any one. To make the search practical, it is done in parallel with a comparator associated with each cache entry. These comparators significantly increase the hardware cost, effectively making fully associative placement practical only for caches with small numbers of blocks.
fully associative cache
A cache structure in which a block can be placed in any location in the cache.
The middle range of designs between direct mapped and fully associative is called set associative. In a set-associative cache, there are a fixed number of locations where each block can be placed. A set-associative cache with n locations for a block is called an n-way set-associative cache. An n-way set-associative cache consists of a number of sets, each of which consists of n blocks. Each block in the memory maps to a unique set in the cache given by the index field, and a block can be placed in any element of that set. Thus, a set-associative placement combines direct-mapped placement and fully associative placement: a block is directly mapped into a set, and then all the blocks in the set are searched for a match. For example, Figure 5.14 shows where block 12 may be placed in a cache with eight blocks total, according to the three block placement policies.
set-associative cache
A cache that has a fixed number of locations (at least two) where each block can be placed.
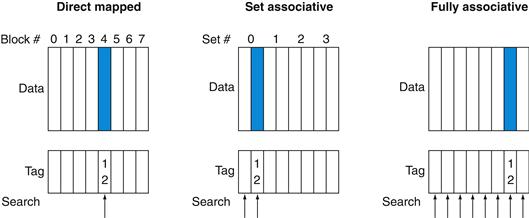
FIGURE 5.14 The location of a memory block whose address is 12 in a cache with eight blocks varies for direct-mapped, set-associative, and fully associative placement.
In direct-mapped placement, there is only one cache block where memory block 12 can be found, and that block is given by (12 modulo 8)=4. In a two-way set-associative cache, there would be four sets, and memory block 12 must be in set (12 mod 4)=0; the memory block could be in either element of the set. In a fully associative placement, the memory block for block address 12 can appear in any of the eight cache blocks.
Remember that in a direct-mapped cache, the position of a memory block is given by
![]()
In a set-associative cache, the set containing a memory block is given by
![]()
Since the block may be placed in any element of the set, all the tags of all the elements of the set must be searched. In a fully associative cache, the block can go anywhere, and all tags of all the blocks in the cache must be searched.
We can also think of all block placement strategies as a variation on set associativity. Figure 5.15 shows the possible associativity structures for an eight-block cache. A direct-mapped cache is simply a one-way set-associative cache: each cache entry holds one block and each set has one element. A fully associative cache with m entries is simply an m-way set-associative cache; it has one set with m blocks, and an entry can reside in any block within that set.
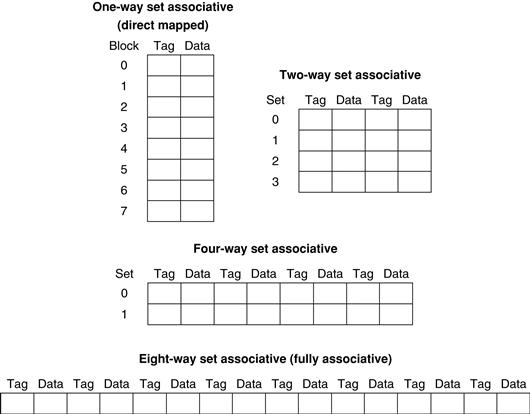
FIGURE 5.15 An eight-block cache configured as direct mapped, two-way set associative, four-way set associative, and fully associative.
The total size of the cache in blocks is equal to the number of sets times the associativity. Thus, for a fixed cache size, increasing the associativity decreases the number of sets while increasing the number of elements per set. With eight blocks, an eight-way set-associative cache is the same as a fully associative cache.
The advantage of increasing the degree of associativity is that it usually decreases the miss rate, as the next example shows. The main disadvantage, which we discuss in more detail shortly, is a potential increase in the hit time.
Misses and Associativity in Caches
Example
Assume there are three small caches, each consisting of four one-word blocks. One cache is fully associative, a second is two-way set-associative, and the third is direct-mapped. Find the number of misses for each cache organization given the following sequence of block addresses: 0, 8, 0, 6, and 8.
Answer
The direct-mapped case is easiest. First, let’s determine to which cache block each block address maps:
|
Block address |
Cache block |
|
0 |
(0 modulo 4)=0 |
|
6 |
(6 modulo 4)=2 |
|
8 |
(8 modulo 4)=0 |
Now we can fill in the cache contents after each reference, using a blank entry to mean that the block is invalid, colored text to show a new entry added to the cache for the associated reference, and plain text to show an old entry in the cache:
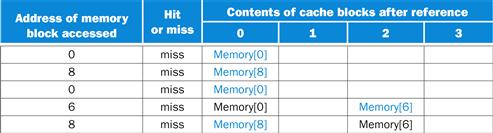
The direct-mapped cache generates five misses for the five accesses.
The set-associative cache has two sets (with indices 0 and 1) with two elements per set. Let’s first determine to which set each block address maps:
|
Block address |
Cache set |
|
0 |
(0 modulo 2)=0 |
|
6 |
(6 modulo 2)=0 |
|
8 |
(8 modulo 2)=0 |
Because we have a choice of which entry in a set to replace on a miss, we need a replacement rule. Set-associative caches usually replace the least recently used block within a set; that is, the block that was used furthest in the past is replaced. (We will discuss other replacement rules in more detail shortly.) Using this replacement rule, the contents of the set-associative cache after each reference looks like this:
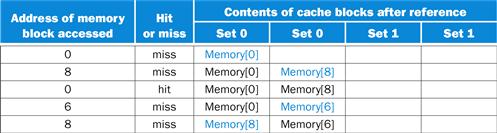
Notice that when block 6 is referenced, it replaces block 8, since block 8 has been less recently referenced than block 0. The two-way set-associative cache has four misses, one less than the direct-mapped cache.
The fully associative cache has four cache blocks (in a single set); any memory block can be stored in any cache block. The fully associative cache has the best performance, with only three misses:
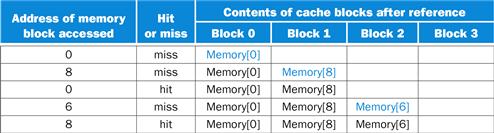
For this series of references, three misses is the best we can do, because three unique block addresses are accessed. Notice that if we had eight blocks in the cache, there would be no replacements in the two-way set-associative cache (check this for yourself), and it would have the same number of misses as the fully associative cache. Similarly, if we had 16 blocks, all 3 caches would have the same number of misses. Even this trivial example shows that cache size and associativity are not independent in determining cache performance.
How much of a reduction in the miss rate is achieved by associativity? Figure 5.16 shows the improvement for a 64 KiB data cache with a 16-word block, and associativity ranging from direct mapped to eight-way. Going from one-way to two-way associativity decreases the miss rate by about 15%, but there is little further improvement in going to higher associativity.

FIGURE 5.16 The data cache miss rates for an organization like the Intrinsity FastMATH processor for SPEC CPU2000 benchmarks with associativity varying from one-way to eight-way.
These results for 10 SPEC CPU2000 programs are from Hennessy and Patterson (2003).
Locating a Block in the Cache
Now, let’s consider the task of finding a block in a cache that is set associative. Just as in a direct-mapped cache, each block in a set-associative cache includes an address tag that gives the block address. The tag of every cache block within the appropriate set is checked to see if it matches the block address from the processor. Figure 5.17 decomposes the address. The index value is used to select the set containing the address of interest, and the tags of all the blocks in the set must be searched. Because speed is of the essence, all the tags in the selected set are searched in parallel. As in a fully associative cache, a sequential search would make the hit time of a set-associative cache too slow.
![]()
FIGURE 5.17 The three portions of an address in a set-associative or direct-mapped cache.
The index is used to select the set, then the tag is used to choose the block by comparison with the blocks in the selected set. The block offset is the address of the desired data within the block.
If the total cache size is kept the same, increasing the associativity increases the number of blocks per set, which is the number of simultaneous compares needed to perform the search in parallel: each increase by a factor of 2 in associativity doubles the number of blocks per set and halves the number of sets. Accordingly, each factor-of-2 increase in associativity decreases the size of the index by 1 bit and increases the size of the tag by 1 bit. In a fully associative cache, there is effectively only one set, and all the blocks must be checked in parallel. Thus, there is no index, and the entire address, excluding the block offset, is compared against the tag of every block. In other words, we search the entire cache without any indexing.
In a direct-mapped cache, only a single comparator is needed, because the entry can be in only one block, and we access the cache simply by indexing. Figure 5.18 shows that in a four-way set-associative cache, four comparators are needed, together with a 4-to-1 multiplexor to choose among the four potential members of the selected set. The cache access consists of indexing the appropriate set and then searching the tags of the set. The costs of an associative cache are the extra comparators and any delay imposed by having to do the compare and select from among the elements of the set.
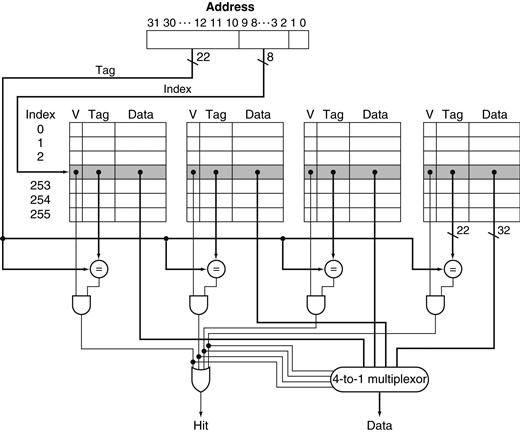
FIGURE 5.18 The implementation of a four-way set-associative cache requires four comparators and a 4-to-1 multiplexor.
The comparators determine which element of the selected set (if any) matches the tag. The output of the comparators is used to select the data from one of the four blocks of the indexed set, using a multiplexor with a decoded select signal. In some implementations, the Output enable signals on the data portions of the cache RAMs can be used to select the entry in the set that drives the output. The Output enable signal comes from the comparators, causing the element that matches to drive the data outputs. This organization eliminates the need for the multiplexor.
The choice among direct-mapped, set-associative, or fully associative mapping in any memory hierarchy will depend on the cost of a miss versus the cost of implementing associativity, both in time and in extra hardware.
Elaboration
A Content Addressable Memory (CAM) is a circuit that combines comparison and storage in a single device. Instead of supplying an address and reading a word like a RAM, you supply the data and the CAM looks to see if it has a copy and returns the index of the matching row. CAMs mean that cache designers can afford to implement much higher set associativity than if they needed to build the hardware out of SRAMs and comparators. In 2013, the greater size and power of CAM generally leads to 2-way and 4-way set associativity being built from standard SRAMs and comparators, with 8-way and above built using CAMs.
Choosing Which Block to Replace
When a miss occurs in a direct-mapped cache, the requested block can go in exactly one position, and the block occupying that position must be replaced. In an associative cache, we have a choice of where to place the requested block, and hence a choice of which block to replace. In a fully associative cache, all blocks are candidates for replacement. In a set-associative cache, we must choose among the blocks in the selected set.
The most commonly used scheme is least recently used (LRU), which we used in the previous example. In an LRU scheme, the block replaced is the one that has been unused for the longest time. The set associative example on page 405 uses LRU, which is why we replaced Memory(0) instead of Memory(6).
least recently used (LRU)
A replacement scheme in which the block replaced is the one that has been unused for the longest time.
LRU replacement is implemented by keeping track of when each element in a set was used relative to the other elements in the set. For a two-way set-associative cache, tracking when the two elements were used can be implemented by keeping a single bit in each set and setting the bit to indicate an element whenever that element is referenced. As associativity increases, implementing LRU gets harder; in Section 5.8, we will see an alternative scheme for replacement.
Size of Tags versus Set Associativity
Example
Increasing associativity requires more comparators and more tag bits per cache block. Assuming a cache of 4096 blocks, a 4-word block size, and a 32-bit address, find the total number of sets and the total number of tag bits for caches that are direct mapped, two-way and four-way set associative, and fully associative.
Answer
Since there are 16 (=24) bytes per block, a 32-bit address yields 32−4=28 bits to be used for index and tag. The direct-mapped cache has the same number of sets as blocks, and hence 12 bits of index, since log2(4096)=12; hence, the total number is (28−12)×4096=16×4096=66 K tag bits.
Each degree of associativity decreases the number of sets by a factor of 2 and thus decreases the number of bits used to index the cache by 1 and increases the number of bits in the tag by 1. Thus, for a two-way set-associative cache, there are 2048 sets, and the total number of tag bits is (28−11)×2×2048=34×2048=70 Kbits. For a four-way set-associative cache, the total number of sets is 1024, and the total number is (28−10)×4×1024=72×1024=74 K tag bits.
For a fully associative cache, there is only one set with 4096 blocks, and the tag is 28 bits, leading to 28×4096×1=115 K tag bits.
Reducing the Miss Penalty Using Multilevel Caches
All modern computers make use of caches. To close the gap further between the fast clock rates of modern processors and the increasingly long time required to access DRAMs, most microprocessors support an additional level of caching. This second-level cache is normally on the same chip and is accessed whenever a miss occurs in the primary cache. If the second-level cache contains the desired data, the miss penalty for the first-level cache will be essentially the access time of the second-level cache, which will be much less than the access time of main memory. If neither the primary nor the secondary cache contains the data, a main memory access is required, and a larger miss penalty is incurred.
How significant is the performance improvement from the use of a secondary cache? The next example shows us.
Performance of Multilevel Caches
Example
Suppose we have a processor with a base CPI of 1.0, assuming all references hit in the primary cache, and a clock rate of 4 GHz. Assume a main memory access time of 100 ns, including all the miss handling. Suppose the miss rate per instruction at the primary cache is 2%. How much faster will the processor be if we add a secondary cache that has a 5 ns access time for either a hit or a miss and is large enough to reduce the miss rate to main memory to 0.5%?
Answer
The miss penalty to main memory is
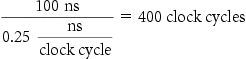
The effective CPI with one level of caching is given by
![]()
For the processor with one level of caching,
![]()
With two levels of caching, a miss in the primary (or first-level) cache can be satisfied either by the secondary cache or by main memory. The miss penalty for an access to the second-level cache is
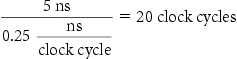
If the miss is satisfied in the secondary cache, then this is the entire miss penalty. If the miss needs to go to main memory, then the total miss penalty is the sum of the secondary cache access time and the main memory access time.
Thus, for a two-level cache, total CPI is the sum of the stall cycles from both levels of cache and the base CPI:
![]()
Thus, the processor with the secondary cache is faster by
![]()
Alternatively, we could have computed the stall cycles by summing the stall cycles of those references that hit in the secondary cache ((2%−0.5%)×20=0.3). Those references that go to main memory, which must include the cost to access the secondary cache as well as the main memory access time, are (0.5%×(20+400)=2.1). The sum, 1.0+0.3+2.1, is again 3.4.
The design considerations for a primary and secondary cache are significantly different, because the presence of the other cache changes the best choice versus a single-level cache. In particular, a two-level cache structure allows the primary cache to focus on minimizing hit time to yield a shorter clock cycle or fewer pipeline stages, while allowing the secondary cache to focus on miss rate to reduce the penalty of long memory access times.
The effect of these changes on the two caches can be seen by comparing each cache to the optimal design for a single level of cache. In comparison to a single-level cache, the primary cache of a multilevel cache is often smaller. Furthermore, the primary cache may use a smaller block size, to go with the smaller cache size and also to reduce the miss penalty. In comparison, the secondary cache will be much larger than in a single-level cache, since the access time of the secondary cache is less critical. With a larger total size, the secondary cache may use a larger block size than appropriate with a single-level cache. It often uses higher associativity than the primary cache given the focus of reducing miss rates.
multilevel cache
A memory hierarchy with multiple levels of caches, rather than just a cache and main memory.
Understanding Program Performance
Sorting has been exhaustively analyzed to find better algorithms: Bubble Sort, Quicksort, Radix Sort, and so on. Figure 5.19(a) shows instructions executed by item searched for Radix Sort versus Quicksort. As expected, for large arrays, Radix Sort has an algorithmic advantage over Quicksort in terms of number of operations. Figure 5.19(b) shows time per key instead of instructions executed. We see that the lines start on the same trajectory as in Figure 5.19(a), but then the Radix Sort line diverges as the data to sort increases. What is going on? Figure 5.19(c) answers by looking at the cache misses per item sorted: Quicksort consistently has many fewer misses per item to be sorted.
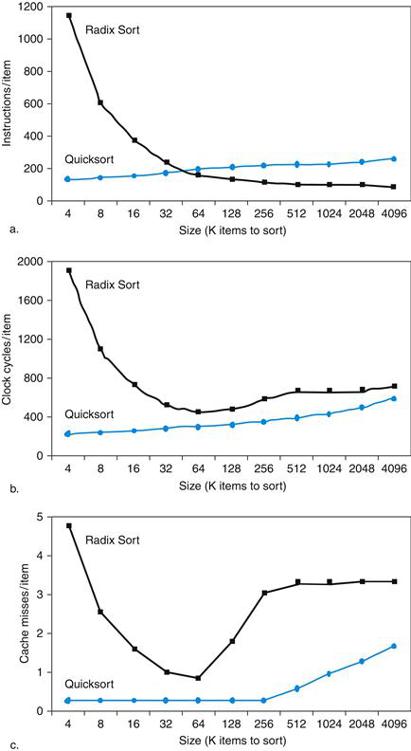
FIGURE 5.19 Comparing Quicksort and Radix Sort by (a) instructions executed per item sorted, (b) time per item sorted, and (c) cache misses per item sorted.
This data is from a paper by LaMarca and Ladner [1996]. Due to such results, new versions of Radix Sort have been invented that take memory hierarchy into account, to regain its algorithmic advantages (see Section 5.15). The basic idea of cache optimizations is to use all the data in a block repeatedly before it is replaced on a miss.
Alas, standard algorithmic analysis often ignores the impact of the memory hierarchy. As faster clock rates and Moore’s Law allow architects to squeeze all of the performance out of a stream of instructions, using the memory hierarchy well is critical to high performance. As we said in the introduction, understanding the behavior of the memory hierarchy is critical to understanding the performance of programs on today’s computers.

Software Optimization via Blocking
Given the importance of the memory hierarchy to program performance, not surprisingly many software optimizations were invented that can dramatically improve performance by reusing data within the cache and hence lower miss rates due to improved temporal locality.
When dealing with arrays, we can get good performance from the memory system if we store the array in memory so that accesses to the array are sequential in memory. Suppose that we are dealing with multiple arrays, however, with some arrays accessed by rows and some by columns. Storing the arrays row-by-row (called row major order) or column-by-column (column major order) does not solve the problem because both rows and columns are used in every loop iteration.
Instead of operating on entire rows or columns of an array, blocked algorithms operate on submatrices or blocks. The goal is to maximize accesses to the data loaded into the cache before the data are replaced; that is, improve temporal locality to reduce cache misses.
For example, the inner loops of DGEMM (lines 4 through 9 of Figure 3.21 in Chapter 3) are

It reads all N-by-N elements of B, reads the same N elements in what corresponds to one row of A repeatedly, and writes what corresponds to one row of N elements of C. (The comments make the rows and columns of the matrices easier to identify.) Figure 5.20 gives a snapshot of the accesses to the three arrays. A dark shade indicates a recent access, a light shade indicates an older access, and white means not yet accessed.
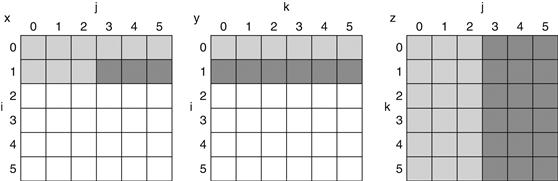
FIGURE 5.20 A snapshot of the three arrays C, A, and B when N=6 and i=1.
The age of accesses to the array elements is indicated by shade: white means not yet touched, light means older accesses, and dark means newer accesses. Compared to Figure 5.21, elements of A and B are read repeatedly to calculate new elements of x. The variables i, j, and k are shown along the rows or columns used to access the arrays.
The number of capacity misses clearly depends on N and the size of the cache. If it can hold all three N-by-N matrices, then all is well, provided there are no cache conflicts. We purposely picked the matrix size to be 32 by 32 in DGEMM for Chapters 3 and 4 so that this would be the case. Each matrix is 32×32=1024 elements and each element is 8 bytes, so the three matrices occupy 24 KiB, which comfortably fit in the 32 KiB data cache of the Intel Core i7 (Sandy Bridge).
If the cache can hold one N-by-N matrix and one row of N, then at least the ith row of A and the array B may stay in the cache. Less than that and misses may occur for both B and C. In the worst case, there would be 2 N3+N2 memory words accessed for N3 operations.
To ensure that the elements being accessed can fit in the cache, the original code is changed to compute on a submatrix. Hence, we essentially invoke the version of DGEMM from Figure 4.80 in Chapter 4repeatedly on matrices of size BLOCKSIZE by BLOCKSIZE. BLOCKSIZE is called the blocking factor.
Figure 5.21 shows the blocked version of DGEMM. The function do_block is DGEMM from Figure 3.21 with three new parameters si, sj, and sk to specify the starting position of each submatrix of of A, B, and C. The two inner loops of the do_block now compute in steps of size BLOCKSIZE rather than the full length of B and C. The gcc optimizer removes any function call overhead by “inlining” the function; that is, it inserts the code directly to avoid the conventional parameter passing and return address bookkeeping instructions.

FIGURE 5.21 Cache blocked version of DGEMM in Figure 3.21.
Assume C is initialized to zero. The do_block function is basically DGEMM from Chapter 3 with new parameters to specify the starting positions of the submatrices of BLOCKSIZE. The gcc optimizer can remove the function overhead instructions by inlining the do_block function.
Figure 5.22 illustrates the accesses to the three arrays using blocking. Looking only at capacity misses, the total number of memory words accessed is 2 N3/BLOCKSIZE+N2. This total is an improvement by about a factor of BLOCKSIZE. Hence, blocking exploits a combination of spatial and temporal locality, since A benefits from spatial locality and B benefits from temporal locality.
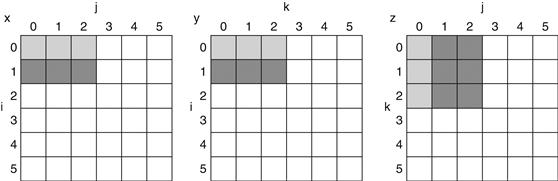
FIGURE 5.22 The age of accesses to the arrays C, A, and B when BLOCKSIZE=3.
Note that, in contrast to Figure 5.20, a smaller number of elements is accessed.
Although we have aimed at reducing cache misses, blocking can also be used to help register allocation. By taking a small blocking size such that the block can be held in registers, we can minimize the number of loads and stores in the program, which also improves performance.
Figure 5.23 shows the impact of cache blocking on the performance of the unoptimized DGEMM as we increase the matrix size beyond where all three matrices fit in the cache. The unoptimized performance is halved for the largest matrix. The cache-blocked version is less than 10% slower even at matrices that are 960×960, or 900 times larger than the 32×32 matrices in Chapters 3 and 4.
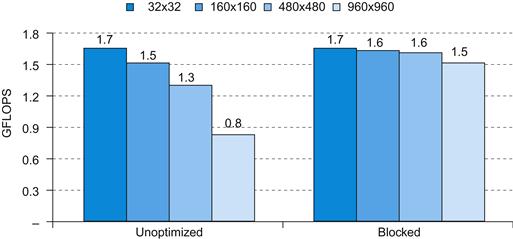
FIGURE 5.23 Performance of unoptimized DGEMM (Figure 3.21) versus cache blocked DGEMM (Figure 5.21) as the matrix dimension varies from 32×32 (where all three matrices fit in the cache) to 960×960.
Elaboration
Multilevel caches create several complications. First, there are now several different types of misses and corresponding miss rates. In the example on pages 410–411, we saw the primary cache miss rate and the global miss rate—the fraction of references that missed in all cache levels. There is also a miss rate for the secondary cache, which is the ratio of all misses in the secondary cache divided by the number of accesses to it. This miss rate is called the local miss rate of the secondary cache. Because the primary cache filters accesses, especially those with good spatial and temporal locality, the local miss rate of the secondary cache is much higher than the global miss rate. For the example on pages 410–411, we can compute the local miss rate of the secondary cache as 0.5%/2%=25%! Luckily, the global miss rate dictates how often we must access the main memory.
global miss rate
The fraction of references that miss in all levels of a multilevel cache.
local miss rate
The fraction of references to one level of a cache that miss; used in multilevel hierarchies.
Elaboration
With out-of-order processors (see Chapter 4), performance is more complex, since they execute instructions during the miss penalty. Instead of instruction miss rates and data miss rates, we use misses per instruction, and this formula:
![]()
There is no general way to calculate overlapped miss latency, so evaluations of memory hierarchies for out-of-order processors inevitably require simulation of the processor and the memory hierarchy. Only by seeing the execution of the processor during each miss can we see if the processor stalls waiting for data or simply finds other work to do. A guideline is that the processor often hides the miss penalty for an L1 cache miss that hits in the L2 cache, but it rarely hides a miss to the L2 cache.
Elaboration
The performance challenge for algorithms is that the memory hierarchy varies between different implementations of the same architecture in cache size, associativity, block size, and number of caches. To cope with such variability, some recent numerical libraries parameterize their algorithms and then search the parameter space at runtime to find the best combination for a particular computer. This approach is called autotuning.
Check Yourself
Which of the following is generally true about a design with multiple levels of caches?
1. First-level caches are more concerned about hit time, and second-level caches are more concerned about miss rate.
2. First-level caches are more concerned about miss rate, and second-level caches are more concerned about hit time.
Summary
In this section, we focused on four topics: cache performance, using associativity to reduce miss rates, the use of multilevel cache hierarchies to reduce miss penalties, and software optimizations to improve effectiveness of caches.
The memory system has a significant effect on program execution time. The number of memory-stall cycles depends on both the miss rate and the miss penalty. The challenge, as we will see in Section 5.8, is to reduce one of these factors without significantly affecting other critical factors in the memory hierarchy.
To reduce the miss rate, we examined the use of associative placement schemes. Such schemes can reduce the miss rate of a cache by allowing more flexible placement of blocks within the cache. Fully associative schemes allow blocks to be placed anywhere, but also require that every block in the cache be searched to satisfy a request. The higher costs make large fully associative caches impractical. Set-associative caches are a practical alternative, since we need only search among the elements of a unique set that is chosen by indexing. Set-associative caches have higher miss rates but are faster to access. The amount of associativity that yields the best performance depends on both the technology and the details of the implementation.
We looked at multilevel caches as a technique to reduce the miss penalty by allowing a larger secondary cache to handle misses to the primary cache. Second-level caches have become commonplace as designers find that limited silicon and the goals of high clock rates prevent primary caches from becoming large. The secondary cache, which is often ten or more times larger than the primary cache, handles many accesses that miss in the primary cache. In such cases, the miss penalty is that of the access time to the secondary cache (typically<10 processor cycles) versus the access time to memory (typically>100 processor cycles). As with associativity, the design tradeoffs between the size of the secondary cache and its access time depend on a number of aspects of the implementation.
Finally, given the importance of the memory hierarchy in performance, we looked at how to change algorithms to improve cache behavior, with blocking being an important technique when dealing with large arrays.
5.5 Dependable Memory Hierarchy
Implicit in all the prior discussion is that the memory hierarchy doesn’t forget. Fast but undependable is not very attractive. As we learned in Chapter 1, the one great idea for dependability is redundancy. In this section we’ll first go over the terms to define terms and measures associated with failure, and then show how redundancy can make nearly unforgettable memories.

Defining Failure
We start with an assumption that you have a specification of proper service. Users can then see a system alternating between two states of delivered service with respect to the service specification:
1. Service accomplishment, where the service is delivered as specified
2. Service interruption, where the delivered service is different from the specified service
Transitions from state 1 to state 2 are caused by failures, and transitions from state 2 to state 1 are called restorations. Failures can be permanent or intermittent. The latter is the more difficult case; it is harder to diagnose the problem when a system oscillates between the two states. Permanent failures are far easier to diagnose.
This definition leads to two related terms: reliability and availability.
Reliability is a measure of the continuous service accomplishment—or, equivalently, of the time to failure—from a reference point. Hence, mean time to failure (MTTF) is a reliability measure. A related term is annual failure rate (AFR), which is just the percentage of devices that would be expected to fail in a year for a given MTTF. When MTTF gets large it can be misleading, while AFR leads to better intuition.
MTTF vs. AFR of Disks
Example
Some disks today are quoted to have a 1,000,000-hour MTTF. As 1,000,000 hours is 1,000,000/(365×24)=114 years, it would seem like they practically never fail. Warehouse scale computers that run Internet services such as Search might have 50,000 servers. Assume each server has 2 disks. Use AFR to calculate how many disks we would expect to fail per year.
Answer
One year is 365×24=8760 hours. A 1,000,000-hour MTTF means an AFR of 8760/1,000,000=0.876%. With 100,000 disks, we would expect 876 disks to fail per year, or on average more than 2 disk failures per day!
Service interruption is measured as mean time to repair (MTTR). Mean time between failures (MTBF) is simply the sum of MTTF+MTTR. Although MTBF is widely used, MTTF is often the more appropriate term. Availability is then a measure of service accomplishment with respect to the alternation between the two states of accomplishment and interruption. Availability is statistically quantified as
![]()
Note that reliability and availability are actually quantifiable measures, rather than just synonyms for dependability. Shrinking MTTR can help availability as much as increasing MTTF. For example, tools for fault detection, diagnosis, and repair can help reduce the time to repair faults and thereby improve availability.
We want availability to be very high. One shorthand is to quote the number of “nines of availability” per year. For example, a very good Internet service today offers 4 or 5 nines of availability. Given 365 days per year, which is 365×24×60=526,000 minutes, then the shorthand is decoded as follows:
One nine: 90%=> 36.5 days of repair/year
Two nines: 99%=> 3.65 days of repair/year
Three nines: 99.9%=> 526 minutes of repair/year
Four nines: 99.99%=> 52.6 minutes of repair/year
Five nines: 99.999%=> 5.26 minutes of repair/year
and so on.
To increase MTTF, you can improve the quality of the components or design systems to continue operation in the presence of components that have failed. Hence, failure needs to be defined with respect to a context, as failure of a component may not lead to a failure of the system. To make this distinction clear, the term fault is used to mean failure of a component. Here are three ways to improve MTTF:
1. Fault avoidance: Preventing fault occurrence by construction.
2. Fault tolerance: Using redundancy to allow the service to comply with the service specification despite faults occurring.
3. Fault forecasting: Predicting the presence and creation of faults, allowing the component to be replaced before it fails.

The Hamming Single Error Correcting, Double Error Detecting Code (SEC/DED)
Richard Hamming invented a popular redundancy scheme for memory, for which he received the Turing Award in 1968. To invent redundant codes, it is helpful to talk about how “close” correct bit patterns can be. What we call the Hamming distance is just the minimum number of bits that are different between any two correct bit patterns. For example, the distance between 011011 and 001111 is two. What happens if the minimum distance between members of a codes is two, and we get a one-bit error? It will turn a valid pattern in a code to an invalid one. Thus, if we can detect whether members of a code are valid or not, we can detect single bit errors, and can say we have a single bit error detection code.
error detection code
A code that enables the detection of an error in data, but not the precise location and, hence, correction of the error.
Hamming used a parity code for error detection. In a parity code, the number of 1 s in a word is counted; the word has odd parity if the number of 1 s is odd and even otherwise. When a word is written into memory, the parity bit is also written (1 for odd, 0 for even). That is, the parity of the N+1 bit word should always be even. Then, when the word is read out, the parity bit is read and checked. If the parity of the memory word and the stored parity bit do not match, an error has occurred.
Example
Calculate the parity of a byte with the value 31ten and show the pattern stored to memory. Assume the parity bit is on the right. Suppose the most significant bit was inverted in memory, and then you read it back. Did you detect the error? What happens if the two most significant bits are inverted?
Answer
31ten is 00011111two, which has five 1 s. To make parity even, we need to write a 1 in the parity bit, or 000111111two. If the most significant bit is inverted when we read it back, we would see 100111111two which has seven 1 s. Since we expect even parity and calculated odd parity, we would signal an error. If the two most significant bits are inverted, we would see 110111111two which has eight 1 s or even parity and we would not signal an error.
If there are 2 bits of error, then a 1-bit parity scheme will not detect any errors, since the parity will match the data with two errors. (Actually, a 1-bit parity scheme can detect any odd number of errors; however, the probability of having 3 errors is much lower than the probability of having two, so, in practice, a 1-bit parity code is limited to detecting a single bit of error.)
Of course, a parity code cannot correct errors, which Hamming wanted to do as well as detect them. If we used a code that had a minimum distance of 3, then any single bit error would be closer to the correct pattern than to any other valid pattern. He came up with an easy to understand mapping of data into a distance 3 code that we call Hamming Error Correction Code (ECC) in his honor. We use extra parity bits to allow the position identification of a single error. Here are the steps to calculate Hamming ECC
1. Start numbering bits from 1 on the left, as opposed to the traditional numbering of the rightmost bit being 0.
2. Mark all bit positions that are powers of 2 as parity bits (positions 1, 2, 4, 8, 16, …).
3. All other bit positions are used for data bits (positions 3, 5, 6, 7, 9, 10, 11, 12, 13, 14, 15, …).
4. The position of parity bit determines sequence of data bits that it checks (Figure 5.24 shows this coverage graphically) is:
■ Bit 1 (0001two) checks bits (1,3,5,7,9,11,…), which are bits where rightmost bit of address is 1 (0001two, 0011two, 0101two, 0111two, 1001two, 1011two,…).
■ Bit 2 (0010two) checks bits (2,3,6,7,10,11,14,15,…), which are the bits where the second bit to the right in the address is 1.
■ Bit 4 (0100two) checks bits (4–7, 12–15, 20–23,…), which are the bits where the third bit to the right in the address is 1.
■ Bit 8 (1000two) checks bits (8–15, 24–31, 40–47,…), which are the bits where the fourth bit to the right in the address is 1.
Note that each data bit is covered by two or more parity bits.
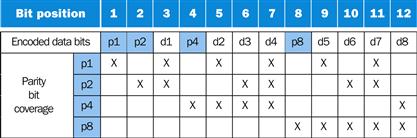
FIGURE 5.24 Parity bits, data bits, and field coverage in a Hamming ECC code for eight data bits.
5. Set parity bits to create even parity for each group.
In what seems like a magic trick, you can then determine whether bits are incorrect by looking at the parity bits. Using the 12 bit code in Figure 5.24, if the value of the four parity calculations (p8,p4,p2,p1) was 0000, then there was no error. However, if the pattern was, say, 1010, which is 10ten, then Hamming ECC tells us that bit 10 (d6) is an error. Since the number is binary, we can correct the error just by inverting the value of bit 10.
Example
Assume one byte data value is 10011010two. First show the Hamming ECC code for that byte, and then invert bit 10 and show that the ECC code finds and corrects the single bit error.
Answer
Leaving spaces for the parity bits, the 12 bit pattern is_ 1 0 0 1_ 1 0 1 0.
Position 1 checks bits 1,3,5,7,9, and 11, which we highlight: __ 1_ 0 0 1_ 1 0 1 0. To make the group even parity, we should set bit 1 to 0.
Position 2 checks bits 2,3,6,7,10,11, which is 0 _ 1_ 0 0 1_ 1 0 1 0 or odd parity, so we set position 2 to a 1.
Position 4 checks bits 4,5,6,7,12, which is 0 1 1 _ 0 0 1_ 1 0 1, so we set it to a 1.
Position 8 checks bits 8,9,10,11,12, which is 0 1 1 1 0 0 1 _ 1 0 1 0, so we set it to a 0.
The final code word is 011100101010. Inverting bit 10 changes it to 011100101110.
Parity bit 1 is 0 (011100101110 is four 1 s, so even parity; this group is OK).
Parity bit 2 is 1 (011100101110 is five 1 s, so odd parity; there is an error somewhere).
Parity bit 4 is 1 (011100101110 is two 1 s, so even parity; this group is OK).
Parity bit 8 is 1 (011100101110 is three 1 s, so odd parity; there is an error somewhere).
Parity bits 2 and 10 are incorrect. As 2+8=10, bit 10 must be wrong. Hence, we can correct the error by inverting bit 10: 011100101010. Voila!
Hamming did not stop at single bit error correction code. At the cost of one more bit, we can make the minimum Hamming distance in a code be 4. This means we can correct single bit errors and detect double bit errors. The idea is to add a parity bit that is calculated over the whole word. Let’s use a four-bit data word as an example, which would only need 7 bits for single bit error detection. Hamming parity bits H (p1 p2 p3) are computed (even parity as usual) plus the even parity over the entire word, p4:
1 2 3 4 5 6 7 8
p1 p2 d1 p3 d2 d3 d4 p4
Then the algorithm to correct one error and detect two is just to calculate parity over the ECC groups (H) as before plus one more over the whole group (p4). There are four cases:
1. H is even and p4 is even, so no error occurred.
2. H is odd and p4 is odd, so a correctable single error occurred. (p4 should calculate odd parity if one error occurred.)
3. H is even and p4 is odd, a single error occurred in p4 bit, not in the rest of the word, so correct the p4 bit.
4. H is odd and p4 is even, a double error occurred. (p4 should calculate even parity if two errors occurred.)
Single Error Correcting Double Error Detecting (SECDED) is common in memory for servers today. Conveniently, eight byte data blocks can get SEC/DED with just one more byte, which is why many DIMMs are 72 bits wide.
Elaboration
To calculate how many bits are needed for SEC, let p be total number of parity bits and d number of data bits in p+d bit word. If p error correction bits are to point to error bit (p+d cases) plus one case to indicate that no error exists, we need:
![]()
For example, for 8 bits data means d=8 and 2p≥p+8+1, so p=4. Similarly, p=5 for 16 bits of data, 6 for 32 bits, 7 for 64 bits, and so on.
Elaboration
In very large systems, the possibility of multiple errors as well as complete failure of a single wide memory chip becomes significant. IBM introduced chipkill to solve this problem, and many very large systems use this technology. (Intel calls their version SDDC.) Similar in nature to the RAID approach used for disks (see ![]() Section 5.11), Chipkill distributes the data and ECC information, so that the complete failure of a single memory chip can be handled by supporting the reconstruction of the missing data from the remaining memory chips. Assuming a 10,000-processor cluster with 4 GiB per processor, IBM calculated the following rates of unrecoverable memory errors in three years of operation:
Section 5.11), Chipkill distributes the data and ECC information, so that the complete failure of a single memory chip can be handled by supporting the reconstruction of the missing data from the remaining memory chips. Assuming a 10,000-processor cluster with 4 GiB per processor, IBM calculated the following rates of unrecoverable memory errors in three years of operation:
■ Parity only—about 90,000, or one unrecoverable (or undetected) failure every 17 minutes.
■ SEC/DED only—about 3500, or about one undetected or unrecoverable failure every 7.5 hours.
■ Chipkill—6, or about one undetected or unrecoverable failure every 2 months.
Hence, Chipkill is a requirement for warehouse-scale computers.
Elaboration
While single or double bit errors are typical for memory systems, networks can have bursts of bit errors. One solution is called Cyclic Redundancy Check. For a block of k bits, a transmitter generates an n-k bit frame check sequence. It transmits n bits exactly divisible by some number. The receiver divides frame by that number. If there is no remainder, it assumes there is no error. If there is, the receiver rejects the message, and asks the transmitter to send again. As you might guess from Chapter 3, it is easy to calculate division for some binary numbers with a shift register, which made CRC codes popular even when hardware was more precious. Going even further, Reed-Solomon codes use Galois fields to correct multibit transmission errors, but now data is considered coefficients of a polynomials and the code space is values of a polynomial. The Reed-Solomon calculation is considerably more complicated than binary division!
5.6 Virtual Machines
Virtual Machines (VM) were first developed in the mid-1960s, and they have remained an important part of mainframe computing over the years. Although largely ignored in the single user PC era in the 1980s and 1990s, they have recently gained popularity due to
■ The increasing importance of isolation and security in modern systems
■ The failures in security and reliability of standard operating systems
■ The sharing of a single computer among many unrelated users, in particular for cloud computing
■ The dramatic increases in raw speed of processors over the decades, which makes the overhead of VMs more acceptable
The broadest definition of VMs includes basically all emulation methods that provide a standard software interface, such as the Java VM. In this section, we are interested in VMs that provide a complete system-level environment at the binary instruction set architecture (ISA) level. Although some VMs run different ISAs in the VM from the native hardware, we assume they always match the hardware. Such VMs are called (Operating) System Virtual Machines. IBM VM/370, VirtualBox, VMware ESX Server, and Xen are examples.
System virtual machines present the illusion that the users have an entire computer to themselves, including a copy of the operating system. A single computer runs multiple VMs and can support a number of different operating systems (OSes). On a conventional platform, a single OS “owns” all the hardware resources, but with a VM, multiple OSes all share the hardware resources.
The software that supports VMs is called a virtual machine monitor (VMM) or hypervisor; the VMM is the heart of virtual machine technology. The underlying hardware platform is called the host, and its resources are shared among the guest VMs. The VMM determines how to map virtual resources to physical resources: a physical resource may be time-shared, partitioned, or even emulated in software. The VMM is much smaller than a traditional OS; the isolation portion of a VMM is perhaps only 10,000 lines of code.
Although our interest here is in VMs for improving protection, VMs provide two other benefits that are commercially significant:
1. Managing software. VMs provide an abstraction that can run the complete software stack, even including old operating systems like DOS. A typical deployment might be some VMs running legacy OSes, many running the current stable OS release, and a few testing the next OS release.
2. Managing hardware. One reason for multiple servers is to have each application running with the compatible version of the operating system on separate computers, as this separation can improve dependability. VMs allow these separate software stacks to run independently yet share hardware, thereby consolidating the number of servers. Another example is that some VMMs support migration of a running VM to a different computer, either to balance load or to evacuate from failing hardware.
Hardware/Software Interface
Amazon Web Services (AWS) uses the virtual machines in its cloud computing offering EC2 for five reasons:
1. It allows AWS to protect users from each other while sharing the same server.
2. It simplifies software distribution within a warehouse scale computer. A customer installs a virtual machine image configured with the appropriate software, and AWS distributes it to all the instances a customer wants to use.
3. Customers (and AWS) can reliably “kill” a VM to control resource usage when customers complete their work.
4. Virtual machines hide the identity of the hardware on which the customer is running, which means AWS can keep using old servers and introduce new, more efficient servers. The customer expects performance for instances to match their ratings in “EC2 Compute Units,” which AWS defines: to “provide the equivalent CPU capacity of a 1.0–1.2 GHz 2007 AMD Opteron or 2007 Intel Xeon processor.” Thanks to Moore’s Law, newer servers clearly offer more EC2 Compute Units than older ones, but AWS can keep renting old servers as long as they are economical.

5. Virtual Machine Monitors can control the rate that a VM uses the processor, the network, and disk space, which allows AWS to offer many price points of instances of different types running on the same underlying servers. For example, in 2012 AWS offered 14 instance types, from small standard instances at $0.08 per hour to high I/O quadruple extra large instances at $3.10 per hour.
In general, the cost of processor virtualization depends on the workload. User-level processor-bound programs have zero virtualization overhead, because the OS is rarely invoked, so everything runs at native speeds. I/O-intensive workloads are generally also OS-intensive, executing many system calls and privileged instructions that can result in high virtualization overhead. On the other hand, if the I/O-intensive workload is also I/O-bound, the cost of processor virtualization can be completely hidden, since the processor is often idle waiting for I/O.
The overhead is determined by both the number of instructions that must be emulated by the VMM and by how much time each takes to emulate them. Hence, when the guest VMs run the same ISA as the host, as we assume here, the goal of the architecture and the VMM is to run almost all instructions directly on the native hardware.
Requirements of a Virtual Machine Monitor
What must a VM monitor do? It presents a software interface to guest software, it must isolate the state of guests from each other, and it must protect itself from guest software (including guest OSes). The qualitative requirements are:
■ Guest software should behave on a VM exactly as if it were running on the native hardware, except for performance-related behavior or limitations of fixed resources shared by multiple VMs.
■ Guest software should not be able to change allocation of real system resources directly.
To “virtualize” the processor, the VMM must control just about everything—access to privileged state, I/O, exceptions, and interrupts—even though the guest VM and OS currently running are temporarily using them.
For example, in the case of a timer interrupt, the VMM would suspend the currently running guest VM, save its state, handle the interrupt, determine which guest VM to run next, and then load its state. Guest VMs that rely on a timer interrupt are provided with a virtual timer and an emulated timer interrupt by the VMM.
To be in charge, the VMM must be at a higher privilege level than the guest VM, which generally runs in user mode; this also ensures that the execution of any privileged instruction will be handled by the VMM. The basic requirements of system virtual:
■ At least two processor modes, system and user.
■ A privileged subset of instructions that is available only in system mode, resulting in a trap if executed in user mode; all system resources must be controllable only via these instructions.
(Lack of) Instruction Set Architecture Support for Virtual Machines
If VMs are planned for during the design of the ISA, it’s relatively easy to reduce both the number of instructions that must be executed by a VMM and improve their emulation speed. An architecture that allows the VM to execute directly on the hardware earns the title virtualizable, and the IBM 370 architecture proudly bears that label.
Alas, since VMs have been considered for PC and server applications only fairly recently, most instruction sets were created without virtualization in mind. These culprits include x86 and most RISC architectures, including ARMv7 and MIPS.
Because the VMM must ensure that the guest system only interacts with virtual resources, a conventional guest OS runs as a user mode program on top of the VMM. Then, if a guest OS attempts to access or modify information related to hardware resources via a privileged instruction—for example, reading or writing a status bit that enables interrupts—it will trap to the VMM. The VMM can then effect the appropriate changes to corresponding real resources.
Hence, if any instruction that tries to read or write such sensitive information traps when executed in user mode, the VMM can intercept it and support a virtual version of the sensitive information, as the guest OS expects.
In the absence of such support, other measures must be taken. A VMM must take special precautions to locate all problematic instructions and ensure that they behave correctly when executed by a guest OS, thereby increasing the complexity of the VMM and reducing the performance of running the VM.
Protection and Instruction Set Architecture
Protection is a joint effort of architecture and operating systems, but architects had to modify some awkward details of existing instruction set architectures when virtual memory became popular.
For example, the x86 instruction POPF loads the flag registers from the top of the stack in memory. One of the flags is the Interrupt Enable (IE) flag. If you run the POPF instruction in user mode, rather than trap it, it simply changes all the flags except IE. In system mode, it does change the IE. Since a guest OS runs in user mode inside a VM, this is a problem, as it expects to see a changed IE.
Historically, IBM mainframe hardware and VMM took three steps to improve performance of virtual machines:
1. Reduce the cost of processor virtualization.
2. Reduce interrupt overhead cost due to the virtualization.
3. Reduce interrupt cost by steering interrupts to the proper VM without invoking VMM.
AMD and Intel tried to address the first point in 2006 by reducing the cost of processor virtualization. It will be interesting to see how many generations of architecture and VMM modifications it will take to address all three points, and how long before virtual machines of the 21st century will be as efficient as the IBM mainframes and VMMs of the 1970s.
5.7 Virtual Memory
… a system has been devised to make the core drum combination appear to the programmer as a single level store, the requisite transfers taking place automatically.
Kilburn et al., One-level storage system, 1962
In earlier sections, we saw how caches provided fast access to recently used portions of a program’s code and data. Similarly, the main memory can act as a “cache” for the secondary storage, usually implemented with magnetic disks. This technique is called virtual memory. Historically, there were two major motivations for virtual memory: to allow efficient and safe sharing of memory among multiple programs, such as for the memory needed by multiple virtual machines for cloud computing, and to remove the programming burdens of a small, limited amount of main memory. Five decades after its invention, it’s the former reason that reigns today.
virtual memory
A technique that uses main memory as a “cache” for secondary storage.
Of course, to allow multiple virtual machines to share the same memory, we must be able to protect the virtual machines from each other, ensuring that a program can only read and write the portions of main memory that have been assigned to it. Main memory need contain only the active portions of the many virtual machines, just as a cache contains only the active portion of one program. Thus, the principle of locality enables virtual memory as well as caches, and virtual memory allows us to efficiently share the processor as well as the main memory.
We cannot know which virtual machines will share the memory with other virtual machines when we compile them. In fact, the virtual machines sharing the memory change dynamically while the virtual machines are running. Because of this dynamic interaction, we would like to compile each program into its own address space—a separate range of memory locations accessible only to this program. Virtual memory implements the translation of a program’s address space to physical addresses. This translation process enforces protection of a program’s address space from other virtual machines.
physical address
An address in main memory.
protection
A set of mechanisms for ensuring that multiple processes sharing the processor, memory, or I/O devices cannot interfere, intentionally or unintentionally, with one another by reading or writing each other’s data. These mechanisms also isolate the operating system from a user process.
The second motivation for virtual memory is to allow a single user program to exceed the size of primary memory. Formerly, if a program became too large for memory, it was up to the programmer to make it fit. Programmers divided programs into pieces and then identified the pieces that were mutually exclusive. These overlays were loaded or unloaded under user program control during execution, with the programmer ensuring that the program never tried to access an overlay that was not loaded and that the overlays loaded never exceeded the total size of the memory. Overlays were traditionally organized as modules, each containing both code and data. Calls between procedures in different modules would lead to overlaying of one module with another.
As you can well imagine, this responsibility was a substantial burden on programmers. Virtual memory, which was invented to relieve programmers of this difficulty, automatically manages the two levels of the memory hierarchy represented by main memory (sometimes called physical memory to distinguish it from virtual memory) and secondary storage.
Although the concepts at work in virtual memory and in caches are the same, their differing historical roots have led to the use of different terminology. A virtual memory block is called a page, and a virtual memory miss is called a page fault. With virtual memory, the processor produces a virtual address, which is translated by a combination of hardware and software to a physical address, which in turn can be used to access main memory. Figure 5.25 shows the virtually addressed memory with pages mapped to main memory. This process is called address mapping or address translation. Today, the two memory hierarchy levels controlled by virtual memory are usually DRAMs and flash memory in personal mobile devices and DRAMs and magnetic disks in servers (see Section 5.2). If we return to our library analogy, we can think of a virtual address as the title of a book and a physical address as the location of that book in the library, such as might be given by the Library of Congress call number.
page fault
An event that occurs when an accessed page is not present in main memory.
virtual address
An address that corresponds to a location in virtual space and is translated by address mapping to a physical address when memory is accessed.
address translation
Also called address mapping. The process by which a virtual address is mapped to an address used to access memory.
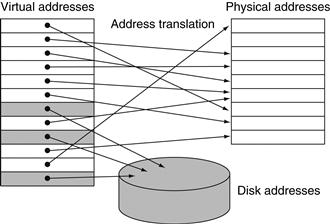
FIGURE 5.25 In virtual memory, blocks of memory (called pages) are mapped from one set of addresses (called virtual addresses) to another set (called physical addresses).
The processor generates virtual addresses while the memory is accessed using physical addresses. Both the virtual memory and the physical memory are broken into pages, so that a virtual page is mapped to a physical page. Of course, it is also possible for a virtual page to be absent from main memory and not be mapped to a physical address; in that case, the page resides on disk. Physical pages can be shared by having two virtual addresses point to the same physical address. This capability is used to allow two different programs to share data or code.
Virtual memory also simplifies loading the program for execution by providing relocation. Relocation maps the virtual addresses used by a program to different physical addresses before the addresses are used to access memory. This relocation allows us to load the program anywhere in main memory. Furthermore, all virtual memory systems in use today relocate the program as a set of fixed-size blocks (pages), thereby eliminating the need to find a contiguous block of memory to allocate to a program; instead, the operating system need only find a sufficient number of pages in main memory.
In virtual memory, the address is broken into a virtual page number and a page offset. Figure 5.26 shows the translation of the virtual page number to a physical page number. The physical page number constitutes the upper portion of the physical address, while the page offset, which is not changed, constitutes the lower portion. The number of bits in the page offset field determines the page size. The number of pages addressable with the virtual address need not match the number of pages addressable with the physical address. Having a larger number of virtual pages than physical pages is the basis for the illusion of an essentially unbounded amount of virtual memory.
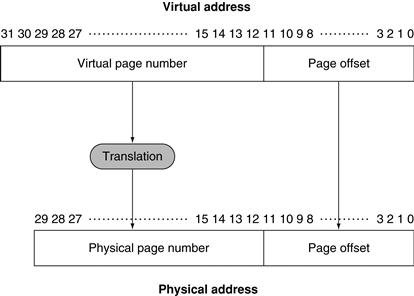
FIGURE 5.26 Mapping from a virtual to a physical address.
The page size is 212=4 KiB. The number of physical pages allowed in memory is 218, since the physical page number has 18 bits in it. Thus, main memory can have at most 1 GiB, while the virtual address space is 4 GiB.
Many design choices in virtual memory systems are motivated by the high cost of a page fault. A page fault to disk will take millions of clock cycles to process. (The table on page 378 shows that main memory latency is about 100,000 times quicker than disk.) This enormous miss penalty, dominated by the time to get the first word for typical page sizes, leads to several key decisions in designing virtual memory systems:
■ Pages should be large enough to try to amortize the high access time. Sizes from 4 KiB to 16 KiB are typical today. New desktop and server systems are being developed to support 32 KiB and 64 KiB pages, but new embedded systems are going in the other direction, to 1 KiB pages.
■ Organizations that reduce the page fault rate are attractive. The primary technique used here is to allow fully associative placement of pages in memory.
■ Page faults can be handled in software because the overhead will be small compared to the disk access time. In addition, software can afford to use clever algorithms for choosing how to place pages because even small reductions in the miss rate will pay for the cost of such algorithms.
■ Write-through will not work for virtual memory, since writes take too long. Instead, virtual memory systems use write-back.
The next few subsections address these factors in virtual memory design.
Elaboration
We present the motivation for virtual memory as many virtual machines sharing the same memory, but virtual memory was originally invented so that many programs could share a computer as part of a timesharing system. Since many readers today have no experience with timesharing systems, we use virtual machines to motivate this section.
Elaboration
For servers and even PCs, 32-bit address processors are problematic. Although we normally think of virtual addresses as much larger than physical addresses, the opposite can occur when the processor address size is small relative to the state of the memory technology. No single program or virtual machine can benefit, but a collection of programs or virtual machines running at the same time can benefit from not having to be swapped to memory or by running on parallel processors.
Elaboration
The discussion of virtual memory in this book focuses on paging, which uses fixed-size blocks. There is also a variable-size block scheme called segmentation. In segmentation, an address consists of two parts: a segment number and a segment offset. The segment number is mapped to a physical address, and the offset is added to find the actual physical address. Because the segment can vary in size, a bounds check is also needed to make sure that the offset is within the segment. The major use of segmentation is to support more powerful methods of protection and sharing in an address space. Most operating system textbooks contain extensive discussions of segmentation compared to paging and of the use of segmentation to logically share the address space. The major disadvantage of segmentation is that it splits the address space into logically separate pieces that must be manipulated as a two-part address: the segment number and the offset. Paging, in contrast, makes the boundary between page number and offset invisible to programmers and compilers.
segmentation
A variable-size address mapping scheme in which an address consists of two parts: a segment number, which is mapped to a physical address, and a segment offset.
Segments have also been used as a method to extend the address space without changing the word size of the computer. Such attempts have been unsuccessful because of the awkwardness and performance penalties inherent in a two-part address, of which programmers and compilers must be aware.
Many architectures divide the address space into large fixed-size blocks that simplify protection between the operating system and user programs and increase the efficiency of implementing paging. Although these divisions are often called “segments,” this mechanism is much simpler than variable block size segmentation and is not visible to user programs; we discuss it in more detail shortly.
Placing a Page and Finding it Again
Because of the incredibly high penalty for a page fault, designers reduce page fault frequency by optimizing page placement. If we allow a virtual page to be mapped to any physical page, the operating system can then choose to replace any page it wants when a page fault occurs. For example, the operating system can use a sophisticated algorithm and complex data structures that track page usage to try to choose a page that will not be needed for a long time. The ability to use a clever and flexible replacement scheme reduces the page fault rate and simplifies the use of fully associative placement of pages.
As mentioned in Section 5.4, the difficulty in using fully associative placement is in locating an entry, since it can be anywhere in the upper level of the hierarchy. A full search is impractical. In virtual memory systems, we locate pages by using a table that indexes the memory; this structure is called a page table, and it resides in memory. A page table is indexed with the page number from the virtual address to discover the corresponding physical page number. Each program has its own page table, which maps the virtual address space of that program to main memory. In our library analogy, the page table corresponds to a mapping between book titles and library locations. Just as the card catalog may contain entries for books in another library on campus rather than the local branch library, we will see that the page table may contain entries for pages not present in memory. To indicate the location of the page table in memory, the hardware includes a register that points to the start of the page table; we call this the page table register. Assume for now that the page table is in a fixed and contiguous area of memory.
page table
The table containing the virtual to physical address translations in a virtual memory system. The table, which is stored in memory, is typically indexed by the virtual page number; each entry in the table contains the physical page number for that virtual page if the page is currently in memory.
Hardware/Software Interface
The page table, together with the program counter and the registers, specifies the state of a virtual machine. If we want to allow another virtual machine to use the processor, we must save this state. Later, after restoring this state, the virtual machine can continue execution. We often refer to this state as a process. The process is considered active when it is in possession of the processor; otherwise, it is considered inactive. The operating system can make a process active by loading the process’s state, including the program counter, which will initiate execution at the value of the saved program counter.
The process’s address space, and hence all the data it can access in memory, is defined by its page table, which resides in memory. Rather than save the entire page table, the operating system simply loads the page table register to point to the page table of the process it wants to make active. Each process has its own page table, since different processes use the same virtual addresses. The operating system is responsible for allocating the physical memory and updating the page tables, so that the virtual address spaces of different processes do not collide. As we will see shortly, the use of separate page tables also provides protection of one process from another.
Figure 5.27 uses the page table register, the virtual address, and the indicated page table to show how the hardware can form a physical address. A valid bit is used in each page table entry, just as we did in a cache. If the bit is off, the page is not present in main memory and a page fault occurs. If the bit is on, the page is in memory and the entry contains the physical page number.

FIGURE 5.27 The page table is indexed with the virtual page number to obtain the corresponding portion of the physical address.
We assume a 32-bit address. The page table pointer gives the starting address of the page table. In this figure, the page size is 212 bytes, or 4 KiB. The virtual address space is 232 bytes, or 4 GiB, and the physical address space is 230 bytes, which allows main memory of up to 1 GiB. The number of entries in the page table is 220, or 1 million entries. The valid bit for each entry indicates whether the mapping is legal. If it is off, then the page is not present in memory. Although the page table entry shown here need only be 19 bits wide, it would typically be rounded up to 32 bits for ease of indexing. The extra bits would be used to store additional information that needs to be kept on a per-page basis, such as protection.
Because the page table contains a mapping for every possible virtual page, no tags are required. In cache terminology, the index that is used to access the page table consists of the full block address, which is the virtual page number.
Page Faults
If the valid bit for a virtual page is off, a page fault occurs. The operating system must be given control. This transfer is done with the exception mechanism, which we saw in Chapter 4 and will discuss again later in this section. Once the operating system gets control, it must find the page in the next level of the hierarchy (usually flash memory or magnetic disk) and decide where to place the requested page in main memory.
The virtual address alone does not immediately tell us where the page is on disk. Returning to our library analogy, we cannot find the location of a library book on the shelves just by knowing its title. Instead, we go to the catalog and look up the book, obtaining an address for the location on the shelves, such as the Library of Congress call number. Likewise, in a virtual memory system, we must keep track of the location on disk of each page in virtual address space.
Because we do not know ahead of time when a page in memory will be replaced, the operating system usually creates the space on flash memory or disk for all the pages of a process when it creates the process. This space is called the swap space. At that time, it also creates a data structure to record where each virtual page is stored on disk. This data structure may be part of the page table or may be an auxiliary data structure indexed in the same way as the page table. Figure 5.28 shows the organization when a single table holds either the physical page number or the disk address.
swap space
The space on the disk reserved for the full virtual memory space of a process.
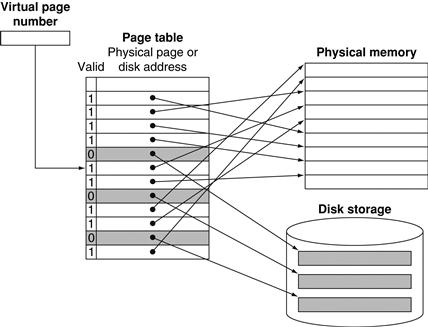
FIGURE 5.28 The page table maps each page in virtual memory to either a page in main memory or a page stored on disk, which is the next level in the hierarchy.
The virtual page number is used to index the page table. If the valid bit is on, the page table supplies the physical page number (i.e., the starting address of the page in memory) corresponding to the virtual page. If the valid bit is off, the page currently resides only on disk, at a specified disk address. In many systems, the table of physical page addresses and disk page addresses, while logically one table, is stored in two separate data structures. Dual tables are justified in part because we must keep the disk addresses of all the pages, even if they are currently in main memory. Remember that the pages in main memory and the pages on disk are the same size.
The operating system also creates a data structure that tracks which processes and which virtual addresses use each physical page. When a page fault occurs, if all the pages in main memory are in use, the operating system must choose a page to replace. Because we want to minimize the number of page faults, most operating systems try to choose a page that they hypothesize will not be needed in the near future. Using the past to predict the future, operating systems follow the least recently used (LRU) replacement scheme, which we mentioned in Section 5.4. The operating system searches for the least recently used page, assuming that a page that has not been used in a long time is less likely to be needed than a more recently accessed page. The replaced pages are written to swap space on the disk. In case you are wondering, the operating system is just another process, and these tables controlling memory are in memory; the details of this seeming contradiction will be explained shortly.
Hardware/Software Interface
Implementing a completely accurate LRU scheme is too expensive, since it requires updating a data structure on every memory reference. Instead, most operating systems approximate LRU by keeping track of which pages have and which pages have not been recently used. To help the operating system estimate the LRU pages, some computers provide a reference bit or use bit, which is set whenever a page is accessed. The operating system periodically clears the reference bits and later records them so it can determine which pages were touched during a particular time period. With this usage information, the operating system can select a page that is among the least recently referenced (detected by having its reference bit off). If this bit is not provided by the hardware, the operating system must find another way to estimate which pages have been accessed.
reference bit
Also called use bit. A field that is set whenever a page is accessed and that is used to implement LRU or other replacement schemes.
Elaboration
With a 32-bit virtual address, 4 KiB pages, and 4 bytes per page table entry, we can compute the total page table size:
![]()
![]()
That is, we would need to use 4 MiB of memory for each program in execution at any time. This amount is not so bad for a single process. What if there are hundreds of processes running, each with their own page table? And how should we handle 64-bit addresses, which by this calculation would need 252 words?
A range of techniques is used to reduce the amount of storage required for the page table. The five techniques below aim at reducing the total maximum storage required as well as minimizing the main memory dedicated to page tables:
1. The simplest technique is to keep a limit register that restricts the size of the page table for a given process. If the virtual page number becomes larger than the contents of the limit register, entries must be added to the page table. This technique allows the page table to grow as a process consumes more space. Thus, the page table will only be large if the process is using many pages of virtual address space. This technique requires that the address space expand in only one direction.
2. Allowing growth in only one direction is not sufficient, since most languages require two areas whose size is expandable: one area holds the stack and the other area holds the heap. Because of this duality, it is convenient to divide the page table and let it grow from the highest address down, as well as from the lowest address up. This means that there will be two separate page tables and two separate limits. The use of two page tables breaks the address space into two segments. The high-order bit of an address usually determines which segment and thus which page table to use for that address. Since the high-order address bit specifies the segment, each segment can be as large as one-half of the address space. A limit register for each segment specifies the current size of the segment, which grows in units of pages. This type of segmentation is used by many architectures, including MIPS. Unlike the type of segmentation discussed in the second elaboration on page 431, this form of segmentation is invisible to the application program, although not to the operating system. The major disadvantage of this scheme is that it does not work well when the address space is used in a sparse fashion rather than as a contiguous set of virtual addresses.
3. Another approach to reducing the page table size is to apply a hashing function to the virtual address so that the page table need be only the size of the number of physical pages in main memory. Such a structure is called an inverted page table. Of course, the lookup process is slightly more complex with an inverted page table, because we can no longer just index the page table.
4. Multiple levels of page tables can also be used to reduce the total amount of page table storage. The first level maps large fixed-size blocks of virtual address space, perhaps 64 to 256 pages in total. These large blocks are sometimes called segments, and this first-level mapping table is sometimes called a segment table, though the segments are again invisible to the user. Each entry in the segment table indicates whether any pages in that segment are allocated and, if so, points to a page table for that segment. Address translation happens by first looking in the segment table, using the highest-order bits of the address. If the segment address is valid, the next set of high-order bits is used to index the page table indicated by the segment table entry. This scheme allows the address space to be used in a sparse fashion (multiple noncontiguous segments can be active) without having to allocate the entire page table. Such schemes are particularly useful with very large address spaces and in software systems that require noncontiguous allocation. The primary disadvantage of this two-level mapping is the more complex process for address translation.
5. To reduce the actual main memory tied up in page tables, most modern systems also allow the page tables to be paged. Although this sounds tricky, it works by using the same basic ideas of virtual memory and simply allowing the page tables to reside in the virtual address space. In addition, there are some small but critical problems, such as a never-ending series of page faults, which must be avoided. How these problems are overcome is both very detailed and typically highly processor specific. In brief, these problems are avoided by placing all the page tables in the address space of the operating system and placing at least some of the page tables for the operating system in a portion of main memory that is physically addressed and is always present and thus never on disk.
What about Writes?
The difference between the access time to the cache and main memory is tens to hundreds of cycles, and write-through schemes can be used, although we need a write buffer to hide the latency of the write from the processor. In a virtual memory system, writes to the next level of the hierarchy (disk) can take millions of processor clock cycles; therefore, building a write buffer to allow the system to write-through to disk would be completely impractical. Instead, virtual memory systems must use write-back, performing the individual writes into the page in memory, and copying the page back to disk when it is replaced in the memory.
Hardware/Software Interface
A write-back scheme has another major advantage in a virtual memory system. Because the disk transfer time is small compared with its access time, copying back an entire page is much more efficient than writing individual words back to the disk. A write-back operation, although more efficient than transferring individual words, is still costly. Thus, we would like to know whether a page needs to be copied back when we choose to replace it. To track whether a page has been written since it was read into the memory, a dirty bit is added to the page table. The dirty bit is set when any word in a page is written. If the operating system chooses to replace the page, the dirty bit indicates whether the page needs to be written out before its location in memory can be given to another page. Hence, a modified page is often called a dirty page.
Making Address Translation Fast: the TLB
Since the page tables are stored in main memory, every memory access by a program can take at least twice as long: one memory access to obtain the physical address and a second access to get the data. The key to improving access performance is to rely on locality of reference to the page table. When a translation for a virtual page number is used, it will probably be needed again in the near future, because the references to the words on that page have both temporal and spatial locality.
Accordingly, modern processors include a special cache that keeps track of recently used translations. This special address translation cache is traditionally referred to as a translation-lookaside buffer (TLB), although it would be more accurate to call it a translation cache. The TLB corresponds to that little piece of paper we typically use to record the location of a set of books we look up in the card catalog; rather than continually searching the entire catalog, we record the location of several books and use the scrap of paper as a cache of Library of Congress call numbers.
translation-lookaside buffer (TLB)
A cache that keeps track of recently used address mappings to try to avoid an access to the page table.
Figure 5.29 shows that each tag entry in the TLB holds a portion of the virtual page number, and each data entry of the TLB holds a physical page number. Because we access the TLB instead of the page table on every reference, the TLB will need to include other status bits, such as the dirty and the reference bits.
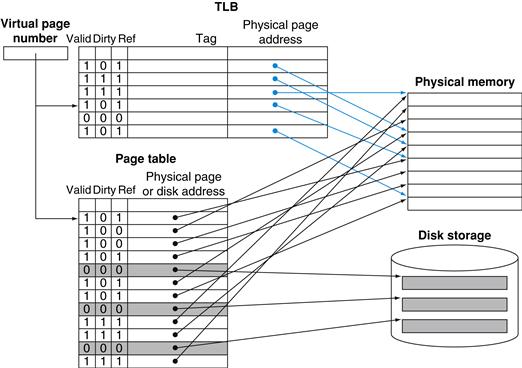
FIGURE 5.29 The TLB acts as a cache of the page table for the entries that map to physical pages only.
The TLB contains a subset of the virtual-to-physical page mappings that are in the page table. The TLB mappings are shown in color. Because the TLB is a cache, it must have a tag field. If there is no matching entry in the TLB for a page, the page table must be examined. The page table either supplies a physical page number for the page (which can then be used to build a TLB entry) or indicates that the page resides on disk, in which case a page fault occurs. Since the page table has an entry for every virtual page, no tag field is needed; in other words, unlike a TLB, a page table is not a cache.
On every reference, we look up the virtual page number in the TLB. If we get a hit, the physical page number is used to form the address, and the corresponding reference bit is turned on. If the processor is performing a write, the dirty bit is also turned on. If a miss in the TLB occurs, we must determine whether it is a page fault or merely a TLB miss. If the page exists in memory, then the TLB miss indicates only that the translation is missing. In such cases, the processor can handle the TLB miss by loading the translation from the page table into the TLB and then trying the reference again. If the page is not present in memory, then the TLB miss indicates a true page fault. In this case, the processor invokes the operating system using an exception. Because the TLB has many fewer entries than the number of pages in main memory, TLB misses will be much more frequent than true page faults.
TLB misses can be handled either in hardware or in software. In practice, with care there can be little performance difference between the two approaches, because the basic operations are the same in either case.
After a TLB miss occurs and the missing translation has been retrieved from the page table, we will need to select a TLB entry to replace. Because the reference and dirty bits are contained in the TLB entry, we need to copy these bits back to the page table entry when we replace an entry. These bits are the only portion of the TLB entry that can be changed. Using write-back—that is, copying these entries back at miss time rather than when they are written—is very efficient, since we expect the TLB miss rate to be small. Some systems use other techniques to approximate the reference and dirty bits, eliminating the need to write into the TLB except to load a new table entry on a miss.
Some typical values for a TLB might be
■ TLB size: 16–512 entries
■ Block size: 1–2 page table entries (typically 4–8 bytes each)
■ Hit time: 0.5–1 clock cycle
■ Miss penalty: 10–100 clock cycles
■ Miss rate: 0.01%–1%
Designers have used a wide variety of associativities in TLBs. Some systems use small, fully associative TLBs because a fully associative mapping has a lower miss rate; furthermore, since the TLB is small, the cost of a fully associative mapping is not too high. Other systems use large TLBs, often with small associativity. With a fully associative mapping, choosing the entry to replace becomes tricky since implementing a hardware LRU scheme is too expensive. Furthermore, since TLB misses are much more frequent than page faults and thus must be handled more cheaply, we cannot afford an expensive software algorithm, as we can for page faults. As a result, many systems provide some support for randomly choosing an entry to replace. We’ll examine replacement schemes in a little more detail in Section 5.8.
The Intrinsity FastMATH TLB
To see these ideas in a real processor, let’s take a closer look at the TLB of the Intrinsity FastMATH. The memory system uses 4 KiB pages and a 32-bit address space; thus, the virtual page number is 20 bits long, as in the top of Figure 5.30. The physical address is the same size as the virtual address. The TLB contains 16 entries, it is fully associative, and it is shared between the instruction and data references. Each entry is 64 bits wide and contains a 20-bit tag (which is the virtual page number for that TLB entry), the corresponding physical page number (also 20 bits), a valid bit, a dirty bit, and other bookkeeping bits. Like most MIPS systems, it uses software to handle TLB misses.
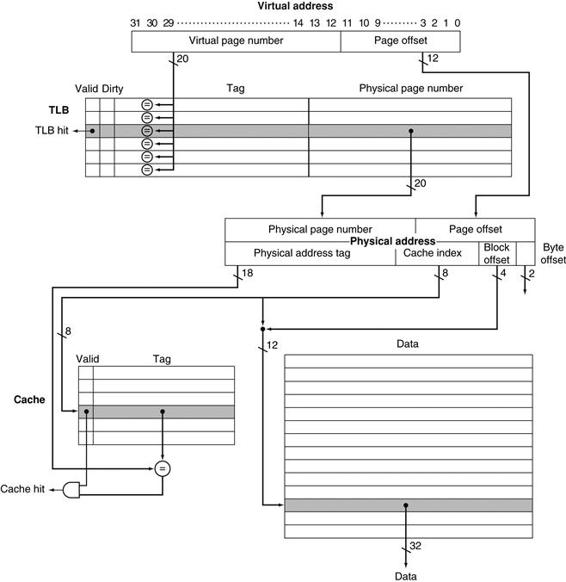
FIGURE 5.30 The TLB and cache implement the process of going from a virtual address to a data item in the Intrinsity FastMATH.
This figure shows the organization of the TLB and the data cache, assuming a 4 KiB page size. This diagram focuses on a read; Figure 5.31 describes how to handle writes. Note that unlike Figure 5.12, the tag and data RAMs are split. By addressing the long but narrow data RAM with the cache index concatenated with the block offset, we select the desired word in the block without a 16:1 multiplexor. While the cache is direct mapped, the TLB is fully associative. Implementing a fully associative TLB requires that every TLB tag be compared against the virtual page number, since the entry of interest can be anywhere in the TLB. (See content addressable memories in the Elaboration on page 408.) If the valid bit of the matching entry is on, the access is a TLB hit, and bits from the physical page number together with bits from the page offset form the index that is used to access the cache.
Figure 5.30 shows the TLB and one of the caches, while Figure 5.31 shows the steps in processing a read or write request. When a TLB miss occurs, the MIPS hardware saves the page number of the reference in a special register and generates an exception. The exception invokes the operating system, which handles the miss in software. To find the physical address for the missing page, the TLB miss routine indexes the page table using the page number of the virtual address and the page table register, which indicates the starting address of the active process page table. Using a special set of system instructions that can update the TLB, the operating system places the physical address from the page table into the TLB. A TLB miss takes about 13 clock cycles, assuming the code and the page table entry are in the instruction cache and data cache, respectively. (We will see the MIPS TLB code on page 449.) A true page fault occurs if the page table entry does not have a valid physical address. The hardware maintains an index that indicates the recommended entry to replace; the recommended entry is chosen randomly.
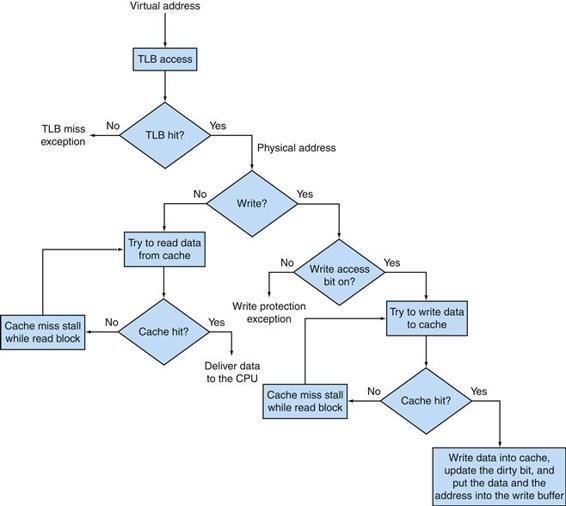
FIGURE 5.31 Processing a read or a write-through in the Intrinsity FastMATH TLB and cache.
If the TLB generates a hit, the cache can be accessed with the resulting physical address. For a read, the cache generates a hit or miss and supplies the data or causes a stall while the data is brought from memory. If the operation is a write, a portion of the cache entry is overwritten for a hit and the data is sent to the write buffer if we assume write-through. A write miss is just like a read miss except that the block is modified after it is read from memory. Write-back requires writes to set a dirty bit for the cache block, and a write buffer is loaded with the whole block only on a read miss or write miss if the block to be replaced is dirty. Notice that a TLB hit and a cache hit are independent events, but a cache hit can only occur after a TLB hit occurs, which means that the data must be present in memory. The relationship between TLB misses and cache misses is examined further in the following example and the exercises at the end of this chapter.
There is an extra complication for write requests: namely, the write access bit in the TLB must be checked. This bit prevents the program from writing into pages for which it has only read access. If the program attempts a write and the write access bit is off, an exception is generated. The write access bit forms part of the protection mechanism, which we will discuss shortly.
Integrating Virtual Memory, TLBs, and Caches
Our virtual memory and cache systems work together as a hierarchy, so that data cannot be in the cache unless it is present in main memory. The operating system helps maintain this hierarchy by flushing the contents of any page from the cache when it decides to migrate that page to disk. At the same time, the OS modifies the page tables and TLB, so that an attempt to access any data on the migrated page will generate a page fault.
Under the best of circumstances, a virtual address is translated by the TLB and sent to the cache where the appropriate data is found, retrieved, and sent back to the processor. In the worst case, a reference can miss in all three components of the memory hierarchy: the TLB, the page table, and the cache. The following example illustrates these interactions in more detail.
Overall Operation of a Memory Hierarchy
Example
In a memory hierarchy like that of Figure 5.30, which includes a TLB and a cache organized as shown, a memory reference can encounter three different types of misses: a TLB miss, a page fault, and a cache miss. Consider all the combinations of these three events with one or more occurring (seven possibilities). For each possibility, state whether this event can actually occur and under what circumstances.
Answer
Figure 5.32 shows all combinations and whether each is possible in practice.

FIGURE 5.32 The possible combinations of events in the TLB, virtual memory system, and cache.
Three of these combinations are impossible, and one is possible (TLB hit, virtual memory hit, cache miss) but never detected.
Elaboration
Figure 5.32 assumes that all memory addresses are translated to physical addresses before the cache is accessed. In this organization, the cache is physically indexed and physically tagged (both the cache index and tag are physical, rather than virtual, addresses). In such a system, the amount of time to access memory, assuming a cache hit, must accommodate both a TLB access and a cache access; of course, these accesses can be pipelined.

Alternatively, the processor can index the cache with an address that is completely or partially virtual. This is called a virtually addressed cache, and it uses tags that are virtual addresses; hence, such a cache is virtually indexed and virtually tagged. In such caches, the address translation hardware (TLB) is unused during the normal cache access, since the cache is accessed with a virtual address that has not been translated to a physical address. This takes the TLB out of the critical path, reducing cache latency. When a cache miss occurs, however, the processor needs to translate the address to a physical address so that it can fetch the cache block from main memory.
virtually addressed cache
A cache that is accessed with a virtual address rather than a physical address.
When the cache is accessed with a virtual address and pages are shared between processes (which may access them with different virtual addresses), there is the possibility of aliasing. Aliasing occurs when the same object has two names—in this case, two virtual addresses for the same page. This ambiguity creates a problem, because a word on such a page may be cached in two different locations, each corresponding to different virtual addresses. This ambiguity would allow one program to write the data without the other program being aware that the data had changed. Completely virtually addressed caches either introduce design limitations on the cache and TLB to reduce aliases or require the operating system, and possibly the user, to take steps to ensure that aliases do not occur.
aliasing
A situation in which two addresses access the same object; it can occur in virtual memory when there are two virtual addresses for the same physical page.
A common compromise between these two design points is caches that are virtually indexed—sometimes using just the page-offset portion of the address, which is really a physical address since it is not translated—but use physical tags. These designs, which are virtually indexed but physically tagged, attempt to achieve the performance advantages of virtually indexed caches with the architecturally simpler advantages of a physically addressed cache. For example, there is no alias problem in this case. Figure 5.30 assumed a 4 KiB page size, but it’s really 16 KiB, so the Intrinsity FastMATH can use this trick. To pull it off, there must be careful coordination between the minimum page size, the cache size, and associativity.
physically addressed cache
A cache that is addressed by a physical address.
Implementing Protection with Virtual Memory
Perhaps the most important function of virtual memory today is to allow sharing of a single main memory by multiple processes, while providing memory protection among these processes and the operating system. The protection mechanism must ensure that although multiple processes are sharing the same main memory, one renegade process cannot write into the address space of another user process or into the operating system either intentionally or unintentionally. The write access bit in the TLB can protect a page from being written. Without this level of protection, computer viruses would be even more widespread.
Hardware/Software Interface
To enable the operating system to implement protection in the virtual memory system, the hardware must provide at least the three basic capabilities summarized below. Note that the first two are the same requirements as needed for virtual machines (Section 5.6).
1. Support at least two modes that indicate whether the running process is a user process or an operating system process, variously called a supervisor process, a kernel process, or an executiveprocess.
supervisor mode
Also called kernel mode. A mode indicating that a running process is an operating system process.
2. Provide a portion of the processor state that a user process can read but not write. This includes the user/supervisor mode bit, which dictates whether the processor is in user or supervisor mode, the page table pointer, and the TLB. To write these elements, the operating system uses special instructions that are only available in supervisor mode.
3. Provide mechanisms whereby the processor can go from user mode to supervisor mode and vice versa. The first direction is typically accomplished by a system call exception, implemented as a special instruction (syscall in the MIPS instruction set) that transfers control to a dedicated location in supervisor code space. As with any other exception, the program counter from the point of the system call is saved in the exception PC (EPC), and the processor is placed in supervisor mode. To return to user mode from the exception, use the return from exception (ERET) instruction, which resets to user mode and jumps to the address in EPC.
system call
A special instruction that transfers control from user mode to a dedicated location in supervisor code space, invoking the exception mechanism in the process.
By using these mechanisms and storing the page tables in the operating system’s address space, the operating system can change the page tables while preventing a user process from changing them, ensuring that a user process can access only the storage provided to it by the operating system.
We also want to prevent a process from reading the data of another process. For example, we wouldn’t want a student program to read the grades while they were in the processor’s memory. Once we begin sharing main memory, we must provide the ability for a process to protect its data from both reading and writing by another process; otherwise, sharing the main memory will be a mixed blessing!
Remember that each process has its own virtual address space. Thus, if the operating system keeps the page tables organized so that the independent virtual pages map to disjoint physical pages, one process will not be able to access another’s data. Of course, this also requires that a user process be unable to change the page table mapping. The operating system can assure safety if it prevents the user process from modifying its own page tables. However, the operating system must be able to modify the page tables. Placing the page tables in the protected address space of the operating system satisfies both requirements.
When processes want to share information in a limited way, the operating system must assist them, since accessing the information of another process requires changing the page table of the accessing process. The write access bit can be used to restrict the sharing to just read sharing, and, like the rest of the page table, this bit can be changed only by the operating system. To allow another process, say, P1, to read a page owned by process P2, P2 would ask the operating system to create a page table entry for a virtual page in P1’s address space that points to the same physical page that P2 wants to share. The operating system could use the write protection bit to prevent P1 from writing the data, if that was P2’s wish. Any bits that determine the access rights for a page must be included in both the page table and the TLB, because the page table is accessed only on a TLB miss.
Elaboration
When the operating system decides to change from running process P1 to running process P2 (called a context switch or process switch), it must ensure that P2 cannot get access to the page tables of P1 because that would compromise protection. If there is no TLB, it suffices to change the page table register to point to P2’s page table (rather than to P1’s); with a TLB, we must clear the TLB entries that belong to P1—both to protect the data of P1 and to force the TLB to load the entries for P2. If the process switch rate were high, this could be quite inefficient. For example, P2 might load only a few TLB entries before the operating system switched back to P1. Unfortunately, P1 would then find that all its TLB entries were gone and would have to pay TLB misses to reload them. This problem arises because the virtual addresses used by P1 and P2 are the same, and we must clear out the TLB to avoid confusing these addresses.
context switch
A changing of the internal state of the processor to allow a different process to use the processor that includes saving the state needed to return to the currently executing process.
A common alternative is to extend the virtual address space by adding a process identifier or task identifier. The Intrinsity FastMATH has an 8-bit address space ID (ASID) field for this purpose. This small field identifies the currently running process; it is kept in a register loaded by the operating system when it switches processes. The process identifier is concatenated to the tag portion of the TLB, so that a TLB hit occurs only if both the page number and the process identifier match. This combination eliminates the need to clear the TLB, except on rare occasions.
Similar problems can occur for a cache, since on a process switch the cache will contain data from the running process. These problems arise in different ways for physically addressed and virtually addressed caches, and a variety of different solutions, such as process identifiers, are used to ensure that a process gets its own data.
Handling TLB Misses and Page Faults
Although the translation of virtual to physical addresses with a TLB is straightforward when we get a TLB hit, as we saw earlier, handling TLB misses and page faults is more complex. A TLB miss occurs when no entry in the TLB matches a virtual address. Recall that a TLB miss can indicate one of two possibilities:
1. The page is present in memory, and we need only create the missing TLB entry.
2. The page is not present in memory, and we need to transfer control to the operating system to deal with a page fault.
MIPS traditionally handles a TLB miss in software. It brings in the page table entry from memory and then re-executes the instruction that caused the TLB miss. Upon re-executing, it will get a TLB hit. If the page table entry indicates the page is not in memory, this time it will get a page fault exception.
Handling a TLB miss or a page fault requires using the exception mechanism to interrupt the active process, transferring control to the operating system, and later resuming execution of the interrupted process. A page fault will be recognized sometime during the clock cycle used to access memory. To restart the instruction after the page fault is handled, the program counter of the instruction that caused the page fault must be saved. Just as in Chapter 4, the exception program counter (EPC) is used to hold this value.
In addition, a TLB miss or page fault exception must be asserted by the end of the same clock cycle that the memory access occurs, so that the next clock cycle will begin exception processing rather than continue normal instruction execution. If the page fault was not recognized in this clock cycle, a load instruction could overwrite a register, and this could be disastrous when we try to restart the instruction. For example, consider the instruction lw $1,0($1): the computer must be able to prevent the write pipeline stage from occurring; otherwise, it could not properly restart the instruction, since the contents of $1 would have been destroyed. A similar complication arises on stores. We must prevent the write into memory from actually completing when there is a page fault; this is usually done by deasserting the write control line to the memory.
Hardware/Software Interface
Between the time we begin executing the exception handler in the operating system and the time that the operating system has saved all the state of the process, the operating system is particularly vulnerable. For example, if another exception occurred when we were processing the first exception in the operating system, the control unit would overwrite the exception program counter, making it impossible to return to the instruction that caused the page fault! We can avoid this disaster by providing the ability to disable and enable exceptions. When an exception first occurs, the processor sets a bit that disables all other exceptions; this could happen at the same time the processor sets the supervisor mode bit. The operating system will then save just enough state to allow it to recover if another exception occurs—namely, the exception program counter (EPC) and Cause registers. EPC and Cause are two of the special control registers that help with exceptions, TLB misses, and page faults; Figure 5.33 shows the rest. The operating system can then re-enable exceptions. These steps make sure that exceptions will not cause the processor to lose any state and thereby be unable to restart execution of the interrupting instruction.
exception enable
Also called interrupt enable. A signal or action that controls whether the process responds to an exception or not; necessary for preventing the occurrence of exceptions during intervals before the processor has safely saved the state needed to restart.
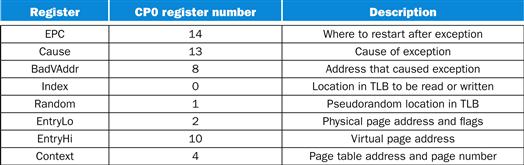
FIGURE 5.33 MIPS control registers.
These are considered to be in coprocessor 0, and hence are read using mfc0 and written using mtc0.
Once the operating system knows the virtual address that caused the page fault, it must complete three steps:
1. Look up the page table entry using the virtual address and find the location of the referenced page on disk.
2. Choose a physical page to replace; if the chosen page is dirty, it must be written out to disk before we can bring a new virtual page into this physical page.
3. Start a read to bring the referenced page from disk into the chosen physical page.
Of course, this last step will take millions of processor clock cycles (so will the second if the replaced page is dirty); accordingly, the operating system will usually select another process to execute in the processor until the disk access completes. Because the operating system has saved the state of the process, it can freely give control of the processor to another process.
When the read of the page from disk is complete, the operating system can restore the state of the process that originally caused the page fault and execute the instruction that returns from the exception. This instruction will reset the processor from kernel to user mode, as well as restore the program counter. The user process then re-executes the instruction that faulted, accesses the requested page successfully, and continues execution.
Page fault exceptions for data accesses are difficult to implement properly in a processor because of a combination of three characteristics:
1. They occur in the middle of instructions, unlike instruction page faults.
2. The instruction cannot be completed before handling the exception.
3. After handling the exception, the instruction must be restarted as if nothing had occurred.
Making instructions restartable, so that the exception can be handled and the instruction later continued, is relatively easy in an architecture like the MIPS. Because each instruction writes only one data item and this write occurs at the end of the instruction cycle, we can simply prevent the instruction from completing (by not writing) and restart the instruction at the beginning.
restartable instruction
An instruction that can resume execution after an exception is resolved without the exception’s affecting the result of the instruction.
Let’s look in more detail at MIPS. When a TLB miss occurs, the MIPS hardware saves the page number of the reference in a special register called BadVAddr and generates an exception.
The exception invokes the operating system, which handles the miss in software. Control is transferred to address 8000 0000hex, the location of the TLB miss handler. To find the physical address for the missing page, the TLB miss routine indexes the page table using the page number of the virtual address and the page table register, which indicates the starting address of the active process page table. To make this indexing fast, MIPS hardware places everything you need in the special Context register: the upper 12 bits have the address of the base of the page table, and the next 18 bits have the virtual address of the missing page. Each page table entry is one word, so the last 2 bits are 0. Thus, the first two instructions copy the Context register into the kernel temporary register $k1 and then load the page table entry from that address into $k1. Recall that $k0 and $k1 are reserved for the operating system to use without saving; a major reason for this convention is to make the TLB miss handler fast. Below is the MIPS code for a typical TLB miss handler:

handler
Name of a software routine invoked to “handle” an exception or interrupt.
As shown above, MIPS has a special set of system instructions to update the TLB. The instruction tlbwr copies from control register EntryLo into the TLB entry selected by the control register Random. Randomimplements random replacement, so it is basically a free-running counter. A TLB miss takes about a dozen clock cycles.
Note that the TLB miss handler does not check to see if the page table entry is valid. Because the exception for TLB entry missing is much more frequent than a page fault, the operating system loads the TLB from the page table without examining the entry and restarts the instruction. If the entry is invalid, another and different exception occurs, and the operating system recognizes the page fault. This method makes the frequent case of a TLB miss fast, at a slight performance penalty for the infrequent case of a page fault.
Once the process that generated the page fault has been interrupted, it transfers control to 8000 0180hex, a different address than the TLB miss handler. This is the general address for exception; TLB miss has a special entry point to lower the penalty for a TLB miss. The operating system uses the exception Cause register to diagnose the cause of the exception. Because the exception is a page fault, the operating system knows that extensive processing will be required. Thus, unlike a TLB miss, it saves the entire state of the active process. This state includes all the general-purpose and floating-point registers, the page table address register, the EPC, and the exception Cause register. Since exception handlers do not usually use the floating-point registers, the general entry point does not save them, leaving that to the few handlers that need them.
Figure 5.34 sketches the MIPS code of an exception handler. Note that we save and restore the state in MIPS code, taking care when we enable and disable exceptions, but we invoke C code to handle the particular exception.
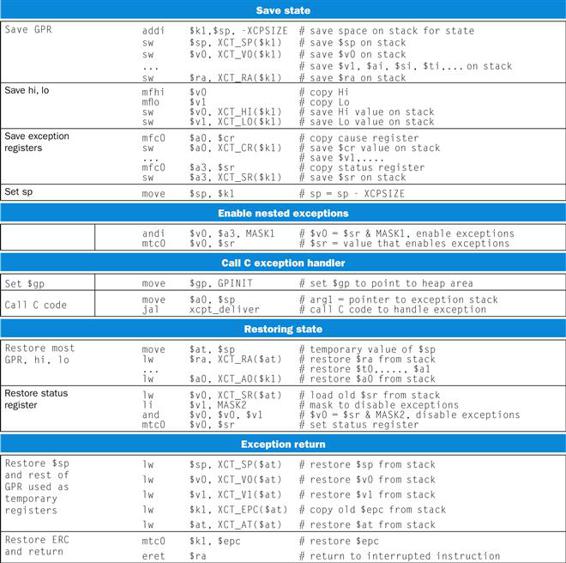
FIGURE 5.34 MIPS code to save and restore state on an exception.
The virtual address that caused the fault depends on whether the fault was an instruction or data fault. The address of the instruction that generated the fault is in the EPC. If it was an instruction page fault, the EPC contains the virtual address of the faulting page; otherwise, the faulting virtual address can be computed by examining the instruction (whose address is in the EPC) to find the base register and offset field.
Elaboration
This simplified version assumes that the stack pointer (sp) is valid. To avoid the problem of a page fault during this low-level exception code, MIPS sets aside a portion of its address space that cannot have page faults, called unmapped. The operating system places the exception entry point code and the exception stack in unmapped memory. MIPS hardware translates virtual addresses 8000 0000hex to BFFF FFFFhex to physical addresses simply by ignoring the upper bits of the virtual address, thereby placing these addresses in the low part of physical memory. Thus, the operating system places exception entry points and exception stacks in unmapped memory.
unmapped
A portion of the address space that cannot have page faults.
Elaboration
The code in Figure 5.34 shows the MIPS-32 exception return sequence. The older MIPS-I architecture uses rfe and jr instead of eret.
Elaboration
For processors with more complex instructions that can touch many memory locations and write many data items, making instructions restartable is much harder. Processing one instruction may generate a number of page faults in the middle of the instruction. For example, x86 processors have block move instructions that touch thousands of data words. In such processors, instructions often cannot be restarted from the beginning, as we do for MIPS instructions. Instead, the instruction must be interrupted and later continued midstream in its execution. Resuming an instruction in the middle of its execution usually requires saving some special state, processing the exception, and restoring that special state. Making this work properly requires careful and detailed coordination between the exception-handling code in the operating system and the hardware.
Elaboration
Rather than pay an extra level of indirection on every memory access, the VMM maintains a shadow page table that maps directly from the guest virtual address space to the physical address space of the hardware. By detecting all modifications to the guest’s page table, the VMM can ensure the shadow page table entries being used by the hardware for translations correspond to those of the guest OS environment, with the exception of the correct physical pages substituted for the real pages in the guest tables. Hence, the VMM must trap any attempt by the guest OS to change its page table or to access the page table pointer. This is commonly done by write protecting the guest page tables and trapping any access to the page table pointer by a guest OS. As noted above, the latter happens naturally if accessing the page table pointer is a privileged operation.
Elaboration
The final portion of the architecture to virtualize is I/O. This is by far the most difficult part of system virtualization because of the increasing number of I/O devices attached to the computer andthe increasing diversity of I/O device types. Another difficulty is the sharing of a real device among multiple VMs, and yet another comes from supporting the myriad of device drivers that are required, especially if different guest OSes are supported on the same VM system. The VM illusion can be maintained by giving each VM generic versions of each type of I/O device driver, and then leaving it to the VMM to handle real I/O.
Elaboration
In addition to virtualizing the instruction set for a virtual machine, another challenge is virtualization of virtual memory, as each guest OS in every virtual machine manages its own set of page tables. To make this work, the VMM separates the notions of real and physical memory (which are often treated synonymously), and makes real memory a separate, intermediate level between virtual memory and physical memory. (Some use the terms virtual memory, physical memory, and machine memory to name the same three levels.) The guest OS maps virtual memory to real memory via its page tables, and the VMM page tables map the guest’s real memory to physical memory. The virtual memory architecture is specified either via page tables, as in IBM VM/370 and the x86, or via the TLB structure, as in MIPS.
Summary
Virtual memory is the name for the level of memory hierarchy that manages caching between the main memory and secondary memory. Virtual memory allows a single program to expand its address space beyond the limits of main memory. More importantly, virtual memory supports sharing of the main memory among multiple, simultaneously active processes, in a protected manner.
Managing the memory hierarchy between main memory and disk is challenging because of the high cost of page faults. Several techniques are used to reduce the miss rate:
1. Pages are made large to take advantage of spatial locality and to reduce the miss rate.
2. The mapping between virtual addresses and physical addresses, which is implemented with a page table, is made fully associative so that a virtual page can be placed anywhere in main memory.
3. The operating system uses techniques, such as LRU and a reference bit, to choose which pages to replace.
Writes to secondary memory are expensive, so virtual memory uses a write-back scheme and also tracks whether a page is unchanged (using a dirty bit) to avoid writing unchanged pages.
The virtual memory mechanism provides address translation from a virtual address used by the program to the physical address space used for accessing memory. This address translation allows protected sharing of the main memory and provides several additional benefits, such as simplifying memory allocation. Ensuring that processes are protected from each other requires that only the operating system can change the address translations, which is implemented by preventing user programs from changing the page tables. Controlled sharing of pages among processes can be implemented with the help of the operating system and access bits in the page table that indicate whether the user program has read or write access to a page.
If a processor had to access a page table resident in memory to translate every access, virtual memory would be too expensive, as caches would be pointless! Instead, a TLB acts as a cache for translations from the page table. Addresses are then translated from virtual to physical using the translations in the TLB.
Caches, virtual memory, and TLBs all rely on a common set of principles and policies. The next section discusses this common framework.
Understanding Program Performance
Although virtual memory was invented to enable a small memory to act as a large one, the performance difference between secondary memory and main memory means that if a program routinely accesses more virtual memory than it has physical memory, it will run very slowly. Such a program would be continuously swapping pages between memory and disk, called thrashing. Thrashing is a disaster if it occurs, but it is rare. If your program thrashes, the easiest solution is to run it on a computer with more memory or buy more memory for your computer. A more complex choice is to re-examine your algorithm and data structures to see if you can change the locality and thereby reduce the number of pages that your program uses simultaneously. This set of popular pages is informally called the working set.
A more common performance problem is TLB misses. Since a TLB might handle only 32–64 page entries at a time, a program could easily see a high TLB miss rate, as the processor may access less than a quarter mebibyte directly: 64×4 KiB=0.25 MiB. For example, TLB misses are often a challenge for Radix Sort. To try to alleviate this problem, most computer architectures now support variable page sizes. For example, in addition to the standard 4 KiB page, MIPS hardware supports 16 KiB, 64 KiB, 256 KiB, 1 MiB, 4 MiB, 16 MiB, 64 MiB, and 256 MiB pages. Hence, if a program uses large page sizes, it can access more memory directly without TLB misses.
The practical challenge is getting the operating system to allow programs to select these larger page sizes. Once again, the more complex solution to reducing TLB misses is to re-examine the algorithm and data structures to reduce the working set of pages; given the importance of memory accesses to performance and the frequency of TLB misses, some programs with large working sets have been redesigned with that goal.
Check Yourself
Match the definitions in the right column to the terms in the left column.

5.8 A Common Framework for Memory Hierarchy
By now, you’ve recognized that the different types of memory hierarchies have a great deal in common. Although many of the aspects of memory hierarchies differ quantitatively, many of the policies and features that determine how a hierarchy functions are similar qualitatively. Figure 5.35 shows how some of the quantitative characteristics of memory hierarchies can differ. In the rest of this section, we will discuss the common operational alternatives for memory hierarchies, and how these determine their behavior. We will examine these policies as a series of four questions that apply between any two levels of a memory hierarchy, although for simplicity we will primarily use terminology for caches.

FIGURE 5.35 The key quantitative design parameters that characterize the major elements of memory hierarchy in a computer.
These are typical values for these levels as of 2012. Although the range of values is wide, this is partially because many of the values that have shifted over time are related; for example, as caches become larger to overcome larger miss penalties, block sizes also grow. While not shown, server microprocessors today also have L3 caches, which can be 2 to 8 MiB and contain many more blocks than L2 caches. L3 caches lower the L2 miss penalty to 30 to 40 clock cycles.
Question 1: Where Can a Block Be Placed?
We have seen that block placement in the upper level of the hierarchy can use a range of schemes, from direct mapped to set associative to fully associative. As mentioned above, this entire range of schemes can be thought of as variations on a set-associative scheme where the number of sets and the number of blocks per set varies:
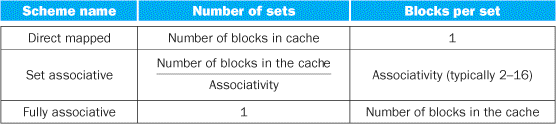
The advantage of increasing the degree of associativity is that it usually decreases the miss rate. The improvement in miss rate comes from reducing misses that compete for the same location. We will examine these in more detail shortly. First, let’s look at how much improvement is gained. Figure 5.36 shows the miss rates for several cache sizes as associativity varies from direct mapped to eight-way set associative. The largest gains are obtained in going from direct mapped to two-way set associative, which yields between a 20% and 30% reduction in the miss rate. As cache sizes grow, the relative improvement from associativity increases only slightly; since the overall miss rate of a larger cache is lower, the opportunity for improving the miss rate decreases and the absolute improvement in the miss rate from associativity shrinks significantly. The potential disadvantages of associativity, as we mentioned earlier, are increased cost and slower access time.
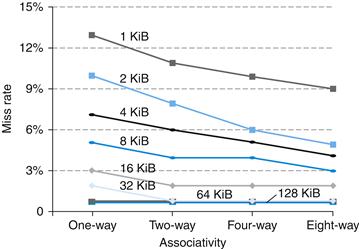
FIGURE 5.36 The data cache miss rates for each of eight cache sizes improve as the associativity increases.
While the benefit of going from one-way (direct mapped) to two-way set associative is significant, the benefits of further associativity are smaller (e.g., 1%–10% improvement going from two-way to four-way versus 20%–30% improvement going from one-way to two-way). There is even less improvement in going from four-way to eight-way set associative, which, in turn, comes very close to the miss rates of a fully associative cache. Smaller caches obtain a significantly larger absolute benefit from associativity because the base miss rate of a small cache is larger. Figure 5.16 explains how this data was collected.
Question 2: How is a Block Found?
The choice of how we locate a block depends on the block placement scheme, since that dictates the number of possible locations. We can summarize the schemes as follows:
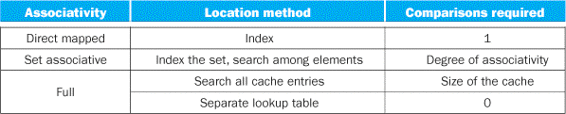
The choice among direct-mapped, set-associative, or fully associative mapping in any memory hierarchy will depend on the cost of a miss versus the cost of implementing associativity, both in time and in extra hardware. Including the L2 cache on the chip enables much higher associativity, because the hit times are not as critical and the designer does not have to rely on standard SRAM chips as the building blocks. Fully associative caches are prohibitive except for small sizes, where the cost of the comparators is not overwhelming and where the absolute miss rate improvements are greatest.
In virtual memory systems, a separate mapping table—the page table—is kept to index the memory. In addition to the storage required for the table, using an index table requires an extra memory access. The choice of full associativity for page placement and the extra table is motivated by these facts:
1. Full associativity is beneficial, since misses are very expensive.
2. Full associativity allows software to use sophisticated replacement schemes that are designed to reduce the miss rate.
3. The full map can be easily indexed with no extra hardware and no searching required.
Therefore, virtual memory systems almost always use fully associative placement.
Set-associative placement is often used for caches and TLBs, where the access combines indexing and the search of a small set. A few systems have used direct-mapped caches because of their advantage in access time and simplicity. The advantage in access time occurs because finding the requested block does not depend on a comparison. Such design choices depend on many details of the implementation, such as whether the cache is on-chip, the technology used for implementing the cache, and the critical role of cache access time in determining the processor cycle time.
Question 3: Which Block Should Be Replaced on a Cache Miss?
When a miss occurs in an associative cache, we must decide which block to replace. In a fully associative cache, all blocks are candidates for replacement. If the cache is set associative, we must choose among the blocks in the set. Of course, replacement is easy in a direct-mapped cache because there is only one candidate.
There are the two primary strategies for replacement in set-associative or fully associative caches:
■ Random: Candidate blocks are randomly selected, possibly using some hardware assistance. For example, MIPS supports random replacement for TLB misses.
■ Least recently used (LRU): The block replaced is the one that has been unused for the longest time.
In practice, LRU is too costly to implement for hierarchies with more than a small degree of associativity (two to four, typically), since tracking the usage information is costly. Even for four-way set associativity, LRU is often approximated—for example, by keeping track of which pair of blocks is LRU (which requires 1 bit), and then tracking which block in each pair is LRU (which requires 1 bit per pair).
For larger associativity, either LRU is approximated or random replacement is used. In caches, the replacement algorithm is in hardware, which means that the scheme should be easy to implement. Random replacement is simple to build in hardware, and for a two-way set-associative cache, random replacement has a miss rate about 1.1 times higher than LRU replacement. As the caches become larger, the miss rate for both replacement strategies falls, and the absolute difference becomes small. In fact, random replacement can sometimes be better than the simple LRU approximations that are easily implemented in hardware.
In virtual memory, some form of LRU is always approximated, since even a tiny reduction in the miss rate can be important when the cost of a miss is enormous. Reference bits or equivalent functionality are often provided to make it easier for the operating system to track a set of less recently used pages. Because misses are so expensive and relatively infrequent, approximating this information primarily in software is acceptable.
Question 4: What Happens on a Write?
A key characteristic of any memory hierarchy is how it deals with writes. We have already seen the two basic options:
■ Write-through: The information is written to both the block in the cache and the block in the lower level of the memory hierarchy (main memory for a cache). The caches in Section 5.3 used this scheme.
■ Write-back: The information is written only to the block in the cache. The modified block is written to the lower level of the hierarchy only when it is replaced. Virtual memory systems always use write-back, for the reasons discussed in Section 5.7.
Both write-back and write-through have their advantages. The key advantages of write-back are the following:
■ Individual words can be written by the processor at the rate that the cache, rather than the memory, can accept them.
■ Multiple writes within a block require only one write to the lower level in the hierarchy.
■ When blocks are written back, the system can make effective use of a high-bandwidth transfer, since the entire block is written.
Write-through has these advantages:
■ Misses are simpler and cheaper because they never require a block to be written back to the lower level.
■ Write-through is easier to implement than write-back, although to be practical, a write-through cache will still need to use a write buffer.
The BIG Picture
Caches, TLBs, and virtual memory may initially look very different, but they rely on the same two principles of locality, and they can be understood by their answers to four questions:
|
Question 1: |
Where can a block be placed? |
|
Answer: |
One place (direct mapped), a few places (set associative), or any place (fully associative). |
|
Question 2: |
How is a block found? |
|
Answer: |
There are four methods: indexing (as in a direct-mapped cache), limited search (as in a set-associative cache), full search (as in a fully associative cache), and a separate lookup table (as in a page table). |
|
Question 3: |
What block is replaced on a miss? |
|
Answer: |
Typically, either the least recently used or a random block. |
|
Question 4: |
How are writes handled? |
|
Answer: |
Each level in the hierarchy can use either write-through or write-back. |
In virtual memory systems, only a write-back policy is practical because of the long latency of a write to the lower level of the hierarchy. The rate at which writes are generated by a processor generally exceeds the rate at which the memory system can process them, even allowing for physically and logically wider memories and burst modes for DRAM. Consequently, today lowest-level caches typically use write-back.
The Three Cs: An Intuitive Model for Understanding the Behavior of Memory Hierarchies
In this subsection, we look at a model that provides insight into the sources of misses in a memory hierarchy and how the misses will be affected by changes in the hierarchy. We will explain the ideas in terms of caches, although the ideas carry over directly to any other level in the hierarchy. In this model, all misses are classified into one of three categories (the three Cs):
three Cs model
A cache model in which all cache misses are classified into one of three categories: compulsory misses, capacity misses, and conflict misses.
■ Compulsory misses: These are cache misses caused by the first access to a block that has never been in the cache. These are also called cold-start misses.
compulsory miss
Also called cold-start miss. A cache miss caused by the first access to a block that has never been in the cache.
■ Capacity misses: These are cache misses caused when the cache cannot contain all the blocks needed during execution of a program. Capacity misses occur when blocks are replaced and then later retrieved.
capacity miss
A cache miss that occurs because the cache, even with full associativity, cannot contain all the blocks needed to satisfy the request.
■ Conflict misses: These are cache misses that occur in set-associative or direct-mapped caches when multiple blocks compete for the same set. Conflict misses are those misses in a direct-mapped or set-associative cache that are eliminated in a fully associative cache of the same size. These cache misses are also called collision misses.
conflict miss
Also called collision miss. A cache miss that occurs in a set-associative or direct-mapped cache when multiple blocks compete for the same set and that are eliminated in a fully associative cache of the same size.
Figure 5.37 shows how the miss rate divides into the three sources. These sources of misses can be directly attacked by changing some aspect of the cache design. Since conflict misses arise directly from contention for the same cache block, increasing associativity reduces conflict misses. Associativity, however, may slow access time, leading to lower overall performance.
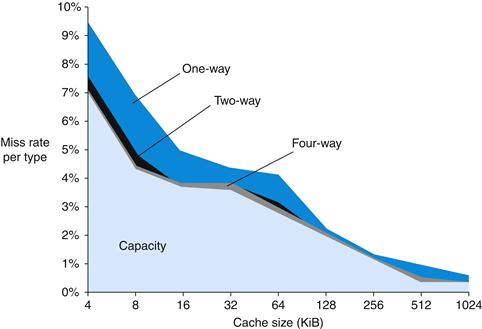
FIGURE 5.37 The miss rate can be broken into three sources of misses.
This graph shows the total miss rate and its components for a range of cache sizes. This data is for the SPEC CPU2000 integer and floating-point benchmarks and is from the same source as the data in Figure 5.36 The compulsory miss component is 0.006% and cannot be seen in this graph. The next component is the capacity miss rate, which depends on cache size. The conflict portion, which depends both on associativity and on cache size, is shown for a range of associativities from one-way to eight-way. In each case, the labeled section corresponds to the increase in the miss rate that occurs when the associativity is changed from the next higher degree to the labeled degree of associativity. For example, the section labeled two-way indicates the additional misses arising when the cache has associativity of two rather than four. Thus, the difference in the miss rate incurred by a direct-mapped cache versus a fully associative cache of the same size is given by the sum of the sections marked four-way, two-way, and one-way. The difference between eight-way and eight-way is so small that it is difficult to see on this graph.
Capacity misses can easily be reduced by enlarging the cache; indeed, second-level caches have been growing steadily larger for many years. Of course, when we make the cache larger, we must also be careful about increasing the access time, which could lead to lower overall performance. Thus, first-level caches have been growing slowly, if at all.
Because compulsory misses are generated by the first reference to a block, the primary way for the cache system to reduce the number of compulsory misses is to increase the block size. This will reduce the number of references required to touch each block of the program once, because the program will consist of fewer cache blocks. As mentioned above, increasing the block size too much can have a negative effect on performance because of the increase in the miss penalty.
The BIG Picture
The challenge in designing memory hierarchies is that every change that potentially improves the miss rate can also negatively affect overall performance, as Figure 5.38 summarizes. This combination of positive and negative effects is what makes the design of a memory hierarchy interesting.
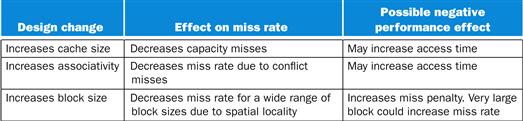
FIGURE 5.38 Memory hierarchy design challenges.
The decomposition of misses into the three Cs is a useful qualitative model. In real cache designs, many of the design choices interact, and changing one cache characteristic will often affect several components of the miss rate. Despite such shortcomings, this model is a useful way to gain insight into the performance of cache designs.
Check Yourself
Which of the following statements (if any) are generally true?
1. There is no way to reduce compulsory misses.
2. Fully associative caches have no conflict misses.
3. In reducing misses, associativity is more important than capacity.
5.9 Using a Finite-State Machine to Control a Simple Cache
We can now implement control for a cache, just as we implemented control for the single-cycle and pipelined datapaths in Chapter 4. This section starts with a definition of a simple cache and then a description of finite-state machines (FSMs). It finishes with the FSM of a controller for this simple cache. ![]() Section 5.12 goes into more depth, showing the cache and controller in a new hardware description language.
Section 5.12 goes into more depth, showing the cache and controller in a new hardware description language.
A Simple Cache
We’re going to design a controller for a simple cache. Here are the key characteristics of the cache:
■ Direct-mapped cache
■ Write-back using write allocate
■ Block size is 4 words (16 bytes or 128 bits)
■ Cache size is 16 KiB, so it holds 1024 blocks
■ 32-byte addresses
■ The cache includes a valid bit and dirty bit per block
From Section 5.3, we can now calculate the fields of an address for the cache:
■ Cache index is 10 bits
■ Block offset is 4 bits
■ Tag size is 32−(10+4) or 18 bits
The signals between the processor to the cache are
■ 1-bit Read or Write signal
■ 1-bit Valid signal, saying whether there is a cache operation or not
■ 32-bit address
■ 32-bit data from processor to cache
■ 32-bit data from cache to processor
■ 1-bit Ready signal, saying the cache operation is complete
The interface between the memory and the cache has the same fields as between the processor and the cache, except that the data fields are now 128 bits wide. The extra memory width is generally found in microprocessors today, which deal with either 32-bit or 64-bit words in the processor while the DRAM controller is often 128 bits. Making the cache block match the width of the DRAM simplified the design. Here are the signals:
■ 1-bit Read or Write signal
■ 1-bit Valid signal, saying whether there is a memory operation or not
■ 32-bit address
■ 128-bit data from cache to memory
■ 128-bit data from memory to cache
■ 1-bit Ready signal, saying the memory operation is complete
Note that the interface to memory is not a fixed number of cycles. We assume a memory controller that will notify the cache via the Ready signal when the memory read or write is finished.
Before describing the cache controller, we need to review finite-state machines, which allow us to control an operation that can take multiple clock cycles.
Finite-State Machines
To design the control unit for the single-cycle datapath, we used a set of truth tables that specified the setting of the control signals based on the instruction class. For a cache, the control is more complex because the operation can be a series of steps. The control for a cache must specify both the signals to be set in any step and the next step in the sequence.
The most common multistep control method is based on finite-state machines, which are usually represented graphically. A finite-state machine consists of a set of states and directions on how to change states. The directions are defined by a next-state function, which maps the current state and the inputs to a new state. When we use a finite-state machine for control, each state also specifies a set of outputs that are asserted when the machine is in that state. The implementation of a finite-state machine usually assumes that all outputs that are not explicitly asserted are deasserted. Similarly, the correct operation of the datapath depends on the fact that a signal that is not explicitly asserted is deasserted, rather than acting as a don’t care.
finite-state machine
A sequential logic function consisting of a set of inputs and outputs, a next-state function that maps the current state and the inputs to a new state, and an output function that maps the current state and possibly the inputs to a set of asserted outputs.
next-state function
A combinational function that, given the inputs and the current state, determines the next state of a finite-state machine.
Multiplexor controls are slightly different, since they select one of the inputs whether they are 0 or 1. Thus, in the finite-state machine, we always specify the setting of all the multiplexor controls that we care about. When we implement the finite-state machine with logic, setting a control to 0 may be the default and thus may not require any gates. A simple example of a finite-state machine appears in Appendix B, and if you are unfamiliar with the concept of a finite-state machine, you may want to examine Appendix B before proceeding.
A finite-state machine can be implemented with a temporary register that holds the current state and a block of combinational logic that determines both the datapath signals to be asserted and the next state. Figure 5.39 shows how such an implementation might look. ![]() Appendix D describes in detail how the finite-state machine is implemented using this structure. In Section B.3, the combinational control logic for a finite-state machine is implemented both with either a ROM (read-only memory) and a PLA (programmable logic array). (Also see Appendix B for a description of these logic elements.)
Appendix D describes in detail how the finite-state machine is implemented using this structure. In Section B.3, the combinational control logic for a finite-state machine is implemented both with either a ROM (read-only memory) and a PLA (programmable logic array). (Also see Appendix B for a description of these logic elements.)
Elaboration
Note that this simple design is called a blocking cache, in that the processor must wait until the cache has finished the request. ![]() Section 5.12 describes the alternative, which is called a nonblockingcache.
Section 5.12 describes the alternative, which is called a nonblockingcache.
Elaboration
The style of finite-state machine in this book is called a Moore machine, after Edward Moore. Its identifying characteristic is that the output depends only on the current state. For a Moore machine, the box labeled combinational control logic can be split into two pieces. One piece has the control output and only the state input, while the other has only the next-state output.
An alternative style of machine is a Mealy machine, named after George Mealy. The Mealy machine allows both the input and the current state to be used to determine the output. Moore machines have potential implementation advantages in speed and size of the control unit. The speed advantages arise because the control outputs, which are needed early in the clock cycle, do not depend on the inputs, but only on the current state. In Appendix B, when the implementation of this finite-state machine is taken down to logic gates, the size advantage can be clearly seen. The potential disadvantage of a Moore machine is that it may require additional states. For example, in situations where there is a one-state difference between two sequences of states, the Mealy machine may unify the states by making the outputs depend on the inputs.
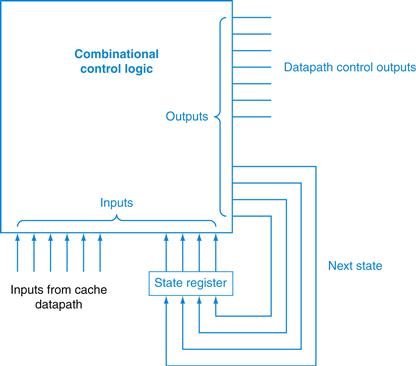
FIGURE 5.39 Finite-state machine controllers are typically implemented using a block of combinational logic and a register to hold the current state.
The outputs of the combinational logic are the next-state number and the control signals to be asserted for the current state. The inputs to the combinational logic are the current state and any inputs used to determine the next state. Notice that in the finite-state machine used in this chapter, the outputs depend only on the current state, not on the inputs. The Elaboration explains this in more detail.
FSM for a Simple Cache Controller
Figure 5.40 shows the four states of our simple cache controller:
■ Idle: This state waits for a valid read or write request from the processor, which moves the FSM to the Compare Tag state.
■ Compare Tag: As the name suggests, this state tests to see if the requested read or write is a hit or a miss. The index portion of the address selects the tag to be compared. If the data in the cache block referred to by the index portion of the address is valid, and the tag portion of the address matches the tag, then it is a hit. Either the data is read from the selected word if it is a load or written to the selected word if it is a store. The Cache Ready signal is then set. If it is a write, the dirty bit is set to 1. Note that a write hit also sets the valid bit and the tag field; while it seems unnecessary, it is included because the tag is a single memory, so to change the dirty bit we also need to change the valid and tag fields. If it is a hit and the block is valid, the FSM returns to the idle state. A miss first updates the cache tag and then goes either to the Write-Back state, if the block at this location has dirty bit value of 1, or to the Allocate state if it is 0.
■ Write-Back: This state writes the 128-bit block to memory using the address composed from the tag and cache index. We remain in this state waiting for the Ready signal from memory. When the memory write is complete, the FSM goes to the Allocate state.
■ Allocate: The new block is fetched from memory. We remain in this state waiting for the Ready signal from memory. When the memory read is complete, the FSM goes to the Compare Tag state. Although we could have gone to a new state to complete the operation instead of reusing the Compare Tag state, there is a good deal of overlap, including the update of the appropriate word in the block if the access was a write.
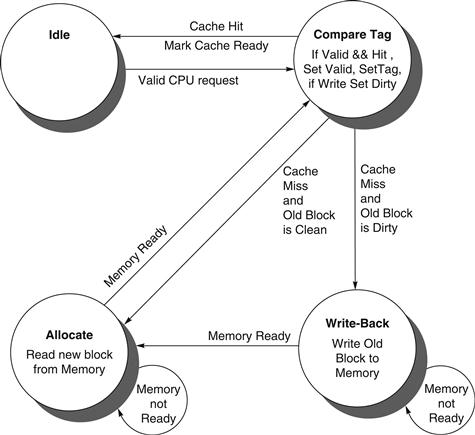
FIGURE 5.40 Four states of the simple controller.
This simple model could easily be extended with more states to try to improve performance. For example, the Compare Tag state does both the compare and the read or write of the cache data in a single clock cycle. Often the compare and cache access are done in separate states to try to improve the clock cycle time. Another optimization would be to add a write buffer so that we could save the dirty block and then read the new block first so that the processor doesn’t have to wait for two memory accesses on a dirty miss. The cache would then write the dirty block from the write buffer while the processor is operating on the requested data.
![]() Section 5.12, goes into more detail about the FSM, showing the full controller in a hardware description language and a block diagram of this simple cache.
Section 5.12, goes into more detail about the FSM, showing the full controller in a hardware description language and a block diagram of this simple cache.
5.10 Parallelism and Memory Hierarchy: Cache Coherence
Given that a multicore multiprocessor means multiple processors on a single chip, these processors very likely share a common physical address space. Caching shared data introduces a new problem, because the view of memory held by two different processors is through their individual caches, which, without any additional precautions, could end up seeing two different values. Figure 5.41 illustrates the problem and shows how two different processors can have two different values for the same location. This difficulty is generally referred to as the cache coherence problem.
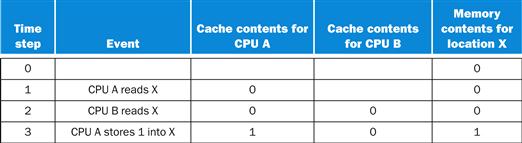
FIGURE 5.41 The cache coherence problem for a single memory location (X), read and written by two processors (A and B).
We initially assume that neither cache contains the variable and that X has the value 0. We also assume a write-through cache; a write-back cache adds some additional but similar complications. After the value of X has been written by A, A’s cache and the memory both contain the new value, but B’s cache does not, and if B reads the value of X, it will receive 0!
Informally, we could say that a memory system is coherent if any read of a data item returns the most recently written value of that data item. This definition, although intuitively appealing, is vague and simplistic; the reality is much more complex. This simple definition contains two different aspects of memory system behavior, both of which are critical to writing correct shared memory programs. The first aspect, called coherence, defines what values can be returned by a read. The second aspect, called consistency, determines when a written value will be returned by a read.
Let’s look at coherence first. A memory system is coherent if
1. A read by a processor P to a location X that follows a write by P to X, with no writes of X by another processor occurring between the write and the read by P, always returns the value written by P. Thus, in Figure 5.41, if CPU A were to read X after time step 3, it should see the value 1.
2. A read by a processor to location X that follows a write by another processor to X returns the written value if the read and write are sufficiently separated in time and no other writes to X occur between the two accesses. Thus, in Figure 5.41, we need a mechanism so that the value 0 in the cache of CPU B is replaced by the value 1 after CPU A stores 1 into memory at address X in time step 3.
3. Writes to the same location are serialized; that is, two writes to the same location by any two processors are seen in the same order by all processors. For example, if CPU B stores 2 into memory at address X after time step 3, processors can never read the value at location X as 2 and then later read it as 1.
The first property simply preserves program order—we certainly expect this property to be true in uniprocessors, for example. The second property defines the notion of what it means to have a coherent view of memory: if a processor could continuously read an old data value, we would clearly say that memory was incoherent.
The need for write serialization is more subtle, but equally important. Suppose we did not serialize writes, and processor P1 writes location X followed by P2 writing location X. Serializing the writes ensures that every processor will see the write done by P2 at some point. If we did not serialize the writes, it might be the case that some processor could see the write of P2 first and then see the write of P1, maintaining the value written by P1 indefinitely. The simplest way to avoid such difficulties is to ensure that all writes to the same location are seen in the same order, which we call write serialization.
Basic Schemes for Enforcing Coherence
In a cache coherent multiprocessor, the caches provide both migration and replication of shared data items:
■ Migration: A data item can be moved to a local cache and used there in a transparent fashion. Migration reduces both the latency to access a shared data item that is allocated remotely and the bandwidth demand on the shared memory.
■ Replication: When shared data are being simultaneously read, the caches make a copy of the data item in the local cache. Replication reduces both latency of access and contention for a read shared data item.
Supporting migration and replication is critical to performance in accessing shared data, so many multiprocessors introduce a hardware protocol to maintain coherent caches. The protocols to maintain coherence for multiple processors are called cache coherence protocols. Key to implementing a cache coherence protocol is tracking the state of any sharing of a data block.
The most popular cache coherence protocol is snooping. Every cache that has a copy of the data from a block of physical memory also has a copy of the sharing status of the block, but no centralized state is kept. The caches are all accessible via some broadcast medium (a bus or network), and all cache controllers monitor or snoop on the medium to determine whether or not they have a copy of a block that is requested on a bus or switch access.
In the following section we explain snooping-based cache coherence as implemented with a shared bus, but any communication medium that broadcasts cache misses to all processors can be used to implement a snooping-based coherence scheme. This broadcasting to all caches makes snooping protocols simple to implement but also limits their scalability.
Snooping Protocols
One method of enforcing coherence is to ensure that a processor has exclusive access to a data item before it writes that item. This style of protocol is called a write invalidate protocol because it invalidates copies in other caches on a write. Exclusive access ensures that no other readable or writable copies of an item exist when the write occurs: all other cached copies of the item are invalidated.
Figure 5.42 shows an example of an invalidation protocol for a snooping bus with write-back caches in action. To see how this protocol ensures coherence, consider a write followed by a read by another processor: since the write requires exclusive access, any copy held by the reading processor must be invalidated (hence the protocol name). Thus, when the read occurs, it misses in the cache, and the cache is forced to fetch a new copy of the data. For a write, we require that the writing processor have exclusive access, preventing any other processor from being able to write simultaneously. If two processors do attempt to write the same data simultaneously, one of them wins the race, causing the other processor’s copy to be invalidated. For the other processor to complete its write, it must obtain a new copy of the data, which must now contain the updated value. Therefore, this protocol also enforces write serialization.
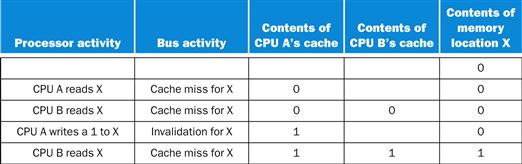
FIGURE 5.42 An example of an invalidation protocol working on a snooping bus for a single cache block (X) with write-back caches.
We assume that neither cache initially holds X and that the value of X in memory is 0. The CPU and memory contents show the value after the processor and bus activity have both completed. A blank indicates no activity or no copy cached. When the second miss by B occurs, CPU A responds with the value canceling the response from memory. In addition, both the contents of B’s cache and the memory contents of X are updated. This update of memory, which occurs when a block becomes shared, simplifies the protocol, but it is possible to track the ownership and force the write-back only if the block is replaced. This requires the introduction of an additional state called “owner,” which indicates that a block may be shared, but the owning processor is responsible for updating any other processors and memory when it changes the block or replaces it.
Hardware/Software Interface
One insight is that block size plays an important role in cache coherency. For example, take the case of snooping on a cache with a block size of eight words, with a single word alternatively written and read by two processors. Most protocols exchange full blocks between processors, thereby increasing coherency bandwidth demands.
Large blocks can also cause what is called false sharing: when two unrelated shared variables are located in the same cache block, the full block is exchanged between processors even though the processors are accessing different variables. Programmers and compilers should lay out data carefully to avoid false sharing.
false sharing
When two unrelated shared variables are located in the same cache block and the full block is exchanged between processors even though the processors are accessing different variables.
Elaboration
Although the three properties on pages 466 and 467 are sufficient to ensure coherence, the question of when a written value will be seen is also important. To see why, observe that we cannot require that a read of X in Figure 5.41 instantaneously sees the value written for X by some other processor. If, for example, a write of X on one processor precedes a read of X on another processor very shortly beforehand, it may be impossible to ensure that the read returns the value of the data written, since the written data may not even have left the processor at that point. The issue of exactly when a written value must be seen by a reader is defined by a memory consistency model.
We make the following two assumptions. First, a write does not complete (and allow the next write to occur) until all processors have seen the effect of that write. Second, the processor does not change the order of any write with respect to any other memory access. These two conditions mean that if a processor writes location X followed by location Y, any processor that sees the new value of Y must also see the new value of X. These restrictions allow the processor to reorder reads, but forces the processor to finish a write in program order.
Elaboration
Since input can change memory behind the caches and since output could need the latest value in a write back cache, there is also a cache coherency problem for I/O with the caches of a single processor as well as just between caches of multiple processors. The cache coherence problem for multiprocessors and I/O (see Chapter 6), although similar in origin, has different characteristics that affect the appropriate solution. Unlike I/O, where multiple data copies are a rare event—one to be avoided whenever possible—a program running on multiple processors will normally have copies of the same data in several caches.
Elaboration
In addition to the snooping cache coherence protocol where the status of shared blocks is distributed, a directory-based cache coherence protocol keeps the sharing status of a block of physical memory in just one location, called the directory. Directory-based coherence has slightly higher implementation overhead than snooping, but it can reduce traffic between caches and thus scale to larger processor counts.
 Parallelism and Memory Hierarchy: Redundant Arrays of Inexpensive Disks
Parallelism and Memory Hierarchy: Redundant Arrays of Inexpensive Disks
This online section describes how using many disks in conjunction can offer much higher throughput, which was the orginal inspiration of Redundant Arrays of Inexpensive Disks (RAID). The real popularlity of RAID, however, was due more to the much greater dependability offered by including a modest number of redundant disks. The section explains the differences in performance, cost, and dependability between the different RAID levels.

 Advanced Material: Implementing Cache Controllers
Advanced Material: Implementing Cache Controllers
This online section shows how to implement control for a cache, just as we implemented control for the single-cycle and pipelined datapaths in Chapter 4. This section starts with a description of finite-state machines and the implemention of a cache controller for a simple data cache, including a description of the cache controller in a hardware description language. It then goes into details of an example cache coherence protocol and the difficulties in implementing such a protocol.
5.13 Real Stuff: The ARM Cortex-A8 and Intel Core i7 Memory Hierarchies
In this section, we will look at the memory hierarchy of the same two microprocessors described in Chapter 4: the ARM Cortex-A8 and Intel Core i7. This section is based on Section 2.6 of Computer Architecture: A Quantitative Approach, 5th edition.
Figure 5.43 summarizes the address sizes and TLBs of the two processors. Note that the A8 has two TLBs with a 32-bit virtual address space and a 32-bit physical address space. The Core i7 has three TLBs with a 48-bit virtual address and a 44-bit physical address. Although the 64-bit registers of the Core i7 could hold a larger virtual address, there was no software need for such a large space and 48-bit virtual addresses shrinks both the page table memory footprint and the TLB hardware.
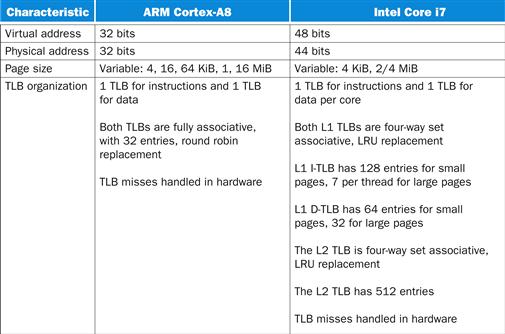
FIGURE 5.43 Address translation and TLB hardware for the ARM Cortex-A8 and Intel Core i7 920.
Both processors provide support for large pages, which are used for things like the operating system or mapping a frame buffer. The large-page scheme avoids using a large number of entries to map a single object that is always present.
Figure 5.44 shows their caches. Keep in mind that the A8 has just one processor or core while the Core i7 has four. Both have identically organized 32 KiB, 4-way set associative, L1 instruction caches (per core) with 64 byte blocks. The A8 uses the same design for data cache, while the Core i7 keeps everything the same except the associativity, which it increases to 8-way. Both use an 8-way set associative unified L2 cache (per core) with 64 byte blocks, although the A8 varies in size from 128 KiB to 1 MiB while the Core i7 is fixed at 256 KiB. As the Core i7 is used for servers, it also offers an L3 cache shared by all the cores on the chip. Its size varies depending on the number of cores. With four cores, as in this case, the size is 8 MiB.
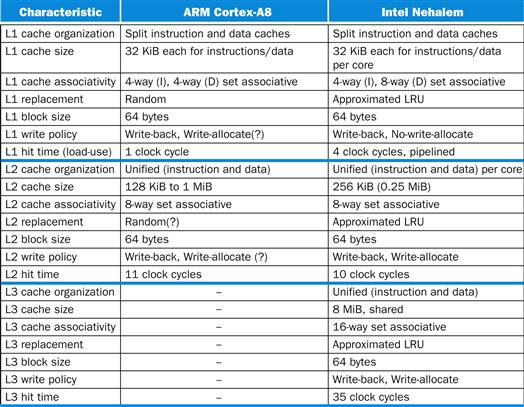
FIGURE 5.44 Caches in the ARM Cortex-A8 and Intel Core i7 920.
A significant challenge facing cache designers is to support processors like the A8 and the Core i7 that can execute more than one memory instruction per clock cycle. A popular technique is to break the cache into banks and allow multiple, independent, parallel accesses, provided the accesses are to different banks. The technique is similar to interleaved DRAM banks (see Section 5.2).

The Core i7 has additional optimizations that allow them to reduce the miss penalty. The first of these is the return of the requested word first on a miss. It also continues to execute instructions that access the data cache during a cache miss. Designers who are attempting to hide the cache miss latency commonly use this technique, called a nonblocking cache, when building out-of-order processors. They implement two flavors of nonblocking. Hit under miss allows additional cache hits during a miss, while miss under miss allows multiple outstanding cache misses. The aim of the first of these two is hiding some miss latency with other work, while the aim of the second is overlapping the latency of two different misses.
nonblocking cache
A cache that allows the processor to make references to the cache while the cache is handling an earlier miss.
Overlapping a large fraction of miss times for multiple outstanding misses requires a high-bandwidth memory system capable of handling multiple misses in parallel. In a personal mobile device, the memory may only be able to take limited advantage of this capability, but large servers and multiprocessors often have memory systems capable of handling more than one outstanding miss in parallel.
The Core i7 has a prefetch mechanism for data accesses. It looks at a pattern of data misses and use this information to try to predict the next address to start fetching the data before the miss occurs. Such techniques generally work best when accessing arrays in loops.
The sophisticated memory hierarchies of these chips and the large fraction of the dies dedicated to caches and TLBs show the significant design effort expended to try to close the gap between processor cycle times and memory latency.
Performance of the A8 and Core i7 Memory Hierarchies
The memory hierarchy of the Cortex-A8 was simulated with a 1 MiB eight-way set associative L2 cache using the integer Minnespec benchmarks. As mentioned in Chapter 4, Minnespec is a set of benchmarks consisting of the SPEC2000 benchmarks but with different inputs that reduce the running times by several orders of magnitude. Although the use of smaller inputs does not change the instruction mix, it does affect the cache behavior. For example, on mcf, the most memory-intensive SPEC2000 integer benchmark, Minnespec has a miss rate for a 32 KiB cache that is only 65% of the miss rate for the full SPEC2000 version. For a 1 MiB cache the difference is a factor of six! For this reason, one cannot compare the Minnespec benchmarks against the SPEC2000 benchmarks, much less the even larger SPEC2006 benchmarks used for the Core i7 in Figure 5.47. Instead, the data are useful for looking at the relative impact of L1 and L2 misses and on overall CPI, which we used in Chapter 4.
The A8 instruction cache miss rates for these benchmarks (and also for the full SPEC2000 versions on which Minnespec is based) are very small even for just the L1: close to zero for most and under 1% for all of them. This low rate probably results from the computationally intensive nature of the SPEC programs and the four-way set associative cache that eliminates most conflict misses. Figure 5.45 shows the data cache results for the A8, which have significant L1 and L2 miss rates. The L1 miss penalty for a 1 GHz Cortex-A8 is 11 clock cycles, while the L2 miss penalty is assumed to be 60 clock cycles. Using these miss penalties, Figure 5.46 shows the average miss penalty per data access.
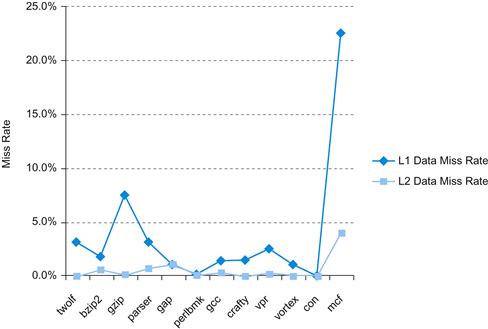
FIGURE 5.45 Data cache miss rates for ARM Cortex-A8 when running Minnespec, a small version of SPEC2000.
Applications with larger memory footprints tend to have higher miss rates in both L1 and L2. Note that the L2 rate is the global miss rate; that is, counting all references, including those that hit in L1. (See Elaboration in Section 5.4.) Mcf is known as a cache buster. Note that this figure is for the same systems and benchmarks as Figure 4.76 in Chapter 4.
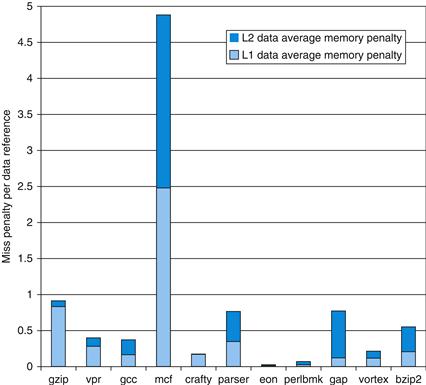
FIGURE 5.46 The average memory access penalty in clock cycles per data memory reference coming from L1 and L2 is shown for the ARM processor when running Minnespec.
Although the miss rates for L1 are significantly higher, the L2 miss penalty, which is more than five times higher, means that the L2 misses can contribute significantly.
Figure 5.47 shows the miss rates for the caches of the Core i7 using the SPEC2006 benchmarks. The L1 instruction cache miss rate varies from 0.1% to 1.8%, averaging just over 0.4%. This rate is in keeping with other studies of instruction cache behavior for the SPECCPU2006 benchmarks, which show low instruction cache miss rates. With L1 data cache miss rates running 5% to 10%, and sometimes higher, the importance of the L2 and L3 caches should be obvious. Since the cost for a miss to memory is over 100 cycles and the average data miss rate in L2 is 4%, L3 is obviously critical. Assuming about half the instructions are loads or stores, without L3 the L2 cache misses could add two cycles per instruction to the CPI! In comparison, the average L3 data miss rate of 1% is still significant but four times lower than the L2 miss rate and six times less than the L1 miss rate.
Elaboration
Because speculation may sometimes be wrong (see Chapter 4), there are references to the L1 data cache that do not correspond to loads or stores that eventually complete execution. The data in Figure 5.45 is measured against all data requests including some that are cancelled. The miss rate when measured against only completed data accesses is 1.6 times higher (an average of 9.5% versus 5.9% for L1 Dcache misses)
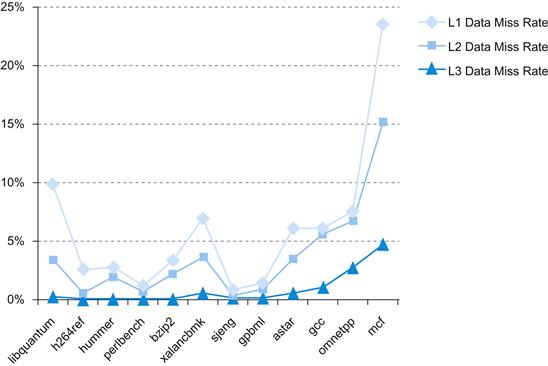
FIGURE 5.47 The L1, L2, and L3 data cache miss rates for the Intel Core i7 920 running the full integer SPECCPU2006 benchmarks.
5.14 Going Faster: Cache Blocking and Matrix Multiply
Our next step in the continuing saga of improving performance of DGEMM by tailoring it to the underlying hardware is to add cache blocking to the subword parallelism and instruction level parallelism optimizations of Chapters 3 and 4. Figure 5.48 shows the blocked version of DGEMM from Figure 4.80. The changes are the same as was made earlier in going from unoptimized DGEMM in Figure 3.21 to blocked DGEMM in Figure 5.21 above. This time we taking the unrolled version of DGEMM from Chapter 4 and invoke it many times on the submatrices of A, B, and C. Indeed, lines 28–34 and lines 7–8 in Figure 5.48 are identical to lines 14–20 and lines 5–6 in Figure 5.21, with the exception of incrementing the for loop in line 7 by the amount unrolled.

FIGURE 5.48 Optimized C version of DGEMM from Figure 4.80 using cache blocking.
These changes are the same ones found in Figure 5.21. The assembly language produced by the compiler for the do_block function is nearly identical to Figure 4.81. Once again, there is no overhead to call the do_block because the compiler inlines the function call.
Unlike the earlier chapters, we do not show the resulting x86 code because the inner loop code is nearly identical to Figure 4.81, as the blocking does not affect the computation, just the order that it accesses data in memory. What does change is the bookkeeping integer instructions to implement the for loops. It expands from 14 instructions before the inner loop and 8 after the loop for Figure 4.80 to 40 and 28 instructions respectively for the bookkeeping code generated for Figure 5.48. Nevertheless, the extra instructions executed pale in comparison to the performance improvement of reducing cache misses. Figure 5.49 compares unoptimzed to optimizations for subword parallelism, instruction level parallelism, and caches. Blocking improves performance over unrolled AVX code by factors of 2 to 2.5 for the larger matrices. When we compare unoptimized code to the code with all three optimizations, the performance improvement is factors of 8 to 15, with the largest increase for the largest matrix.
Elaboration
As mentioned in the Elaboration in Section 3.8, these results are with Turbo mode turned off. As in Chapters 3 and 4, when we turn it on we improve all the results by the temporary increase in the clock rate of 3.3/2.6=1.27. Turbo mode works particularly well in this case because it is using only a single core of an eight-core chip. However, if we want to run fast we should use all cores, which we’ll see in Chapter 6.
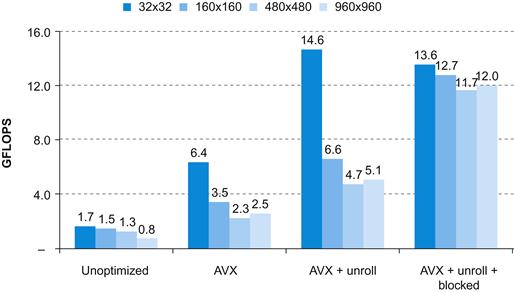
FIGURE 5.49 Performance of four versions of DGEMM from matrix dimensions 32×32 to 960×960.
The fully optimized code for largest matrix is almost 15 times as fast the unoptimized version in Figure 3.21 in Chapter 3.
5.15 Fallacies and Pitfalls
As one of the most naturally quantitative aspects of computer architecture, the memory hierarchy would seem to be less vulnerable to fallacies and pitfalls. Not only have there been many fallacies propagated and pitfalls encountered, but some have led to major negative outcomes. We start with a pitfall that often traps students in exercises and exams.
Pitfall: Ignoring memory system behavior when writing programs or when generating code in a compiler.
This could easily be rewritten as a fallacy: “Programmers can ignore memory hierarchies in writing code.” The evaluation of sort in Figure 5.19 and of cache blocking in Section 5.14 demonstrate that programmers can easily double performance if they factor the behavior of the memory system into the design of their algorithms.
Pitfall: Forgetting to account for byte addressing or the cache block size in simulating a cache.
When simulating a cache (by hand or by computer), we need to make sure we account for the effect of byte addressing and multiword blocks in determining into which cache block a given address maps. For example, if we have a 32-byte direct-mapped cache with a block size of 4 bytes, the byte address 36 maps into block 1 of the cache, since byte address 36 is block address 9 and (9 modulo 8)=1. On the other hand, if address 36 is a word address, then it maps into block (36 mod 8)=4. Make sure the problem clearly states the base of the address.
In like fashion, we must account for the block size. Suppose we have a cache with 256 bytes and a block size of 32 bytes. Into which block does the byte address 300 fall? If we break the address 300 into fields, we can see the answer:
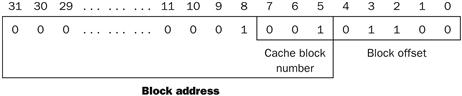
Byte address 300 is block address
![]()
The number of blocks in the cache is
![]()
Block number 9 falls into cache block number (9 modulo 8)=1.
This mistake catches many people, including the authors (in earlier drafts) and instructors who forget whether they intended the addresses to be in words, bytes, or block numbers. Remember this pitfall when you tackle the exercises.
Pitfall: Having less set associativity for a shared cache than the number of cores or threads sharing that cache.
Without extra care, a parallel program running on 2n processors or threads can easily allocate data structures to addresses that would map to the same set of a shared L2 cache. If the cache is at least 2n-way associative, then these accidental conflicts are hidden by the hardware from the program. If not, programmers could face apparently mysterious performance bugs—actually due to L2 conflict misses—when migrating from, say, a 16-core design to 32-core design if both use 16-way associative L2 caches.

Pitfall: Using average memory access time to evaluate the memory hierarchy of an out-of-order processor.
If a processor stalls during a cache miss, then you can separately calculate the memory-stall time and the processor execution time, and hence evaluate the memory hierarchy independently using average memory access time (see page 399).
If the processor continues to execute instructions, and may even sustain more cache misses during a cache miss, then the only accurate assessment of the memory hierarchy is to simulate the out-of-order processor along with the memory hierarchy.
Pitfall: Extending an address space by adding segments on top of an unsegmented address space.
During the 1970s, many programs grew so large that not all the code and data could be addressed with just a 16-bit address. Computers were then revised to offer 32-bit addresses, either through an unsegmented 32-bit address space (also called a flat address space) or by adding 16 bits of segment to the existing 16-bit address. From a marketing point of view, adding segments that were programmer-visible and that forced the programmer and compiler to decompose programs into segments could solve the addressing problem. Unfortunately, there is trouble any time a programming language wants an address that is larger than one segment, such as indices for large arrays, unrestricted pointers, or reference parameters. Moreover, adding segments can turn every address into two words—one for the segment number and one for the segment offset—causing problems in the use of addresses in registers.
Fallacy: Disk failure rates in the field match their specifications.
Two recent studies evaluated large collections of disks to check the relationship between results in the field compared to specifications. One study was of almost 100,000 disks that had quoted MTTF of 1,000,000 to 1,500,000 hours, or AFR of 0.6% to 0.8%. They found AFRs of 2% to 4% to be common, often three to five times higher than the specified rates [Schroeder and Gibson, 2007]. A second study of more than 100,000 disks at Google, which had a quoted AFR of about 1.5%, saw failure rates of 1.7% for drives in their first year rise to 8.6% for drives in their third year, or about five to six times the specified rate [Pinheiro, Weber, and Barroso, 2007].
Fallacy: Operating systems are the best place to schedule disk accesses.
As mentioned in Section 5.2, higher-level disk interfaces offer logical block addresses to the host operating system. Given this high-level abstraction, the best an OS can do to try to help performance is to sort the logical block addresses into increasing order. However, since the disk knows the actual mapping of the logical addresses onto the physical geometry of sectors, tracks, and surfaces, it can reduce the rotational and seek latencies by rescheduling.
For example, suppose the workload is four reads [Anderson, 2003]:
|
Operation |
Starting LBA |
Length |
|
Read |
724 |
8 |
|
Read |
100 |
16 |
|
Read |
9987 |
1 |
|
Read |
26 |
128 |
The host might reorder the four reads into logical block order:
|
Operation |
Starting LBA |
Length |
|
Read |
26 |
128 |
|
Read |
100 |
16 |
|
Read |
724 |
8 |
|
Read |
9987 |
1 |
Depending on the relative location of the data on the disk, reordering could make it worse, as Figure 5.50 shows. The disk-scheduled reads complete in three-quarters of a disk revolution, but the OS-scheduled reads take three revolutions.
Pitfall: Implementing a virtual machine monitor on an instruction set architecture that wasn’t designed to be virtualizable.
FIGURE 5.50 Example showing OS versus disk schedule accesses, labeled host-ordered versus drive-ordered.
The former takes three revolutions to complete the four reads, while the latter completes them in just three-fourths of a revolution (from Anderson [2003]).
Many architects in the 1970s and 1980s weren’t careful to make sure that all instructions reading or writing information related to hardware resource information were privileged. This laissez-faire attitude causes problems for VMMs for all of these architectures, including the x86, which we use here as an example.
Figure 5.51 describes the 18 instructions that cause problems for virtualization [Robin and Irvine, 2000]. The two broad classes are instructions that
■ Read control registers in user mode that reveals that the guest operating system is running in a virtual machine (such as POPF, mentioned earlier)
■ Check protection as required by the segmented architecture but assume that the operating system is running at the highest privilege level
FIGURE 5.51 Summary of 18 x86 instructions that cause problems for virtualization [Robin and Irvine, 2000].
The first five instructions in the top group allow a program in user mode to read a control register, such as descriptor table registers, without causing a trap. The pop flags instruction modifies a control register with sensitive information but fails silently when in user mode. The protection checking of the segmented architecture of the x86 is the downfall of the bottom group, as each of these instructions checks the privilege level implicitly as part of instruction execution when reading a control register. The checking assumes that the OS must be at the highest privilege level, which is not the case for guest VMs. Only the Move to segment register tries to modify control state, and protection checking foils it as well.
To simplify implementations of VMMs on the x86, both AMD and Intel have proposed extensions to the architecture via a new mode. Intel’s VT-x provides a new execution mode for running VMs, an architected definition of the VM state, instructions to swap VMs rapidly, and a large set of parameters to select the circumstances where a VMM must be invoked. Altogether, VT-x adds 11 new instructions for the x86. AMD’s Pacifica makes similar proposals.
An alternative to modifying the hardware is to make small modifications to the operating system to avoid using the troublesome pieces of the architecture. This technique is called paravirtualization, and the open source Xen VMM is a good example. The Xen VMM provides a guest OS with a virtual machine abstraction that uses only the easy-to-virtualize parts of the physical x86 hardware on which the VMM runs.
5.16 Concluding Remarks
The difficulty of building a memory system to keep pace with faster processors is underscored by the fact that the raw material for main memory, DRAMs, is essentially the same in the fastest computers as it is in the slowest and cheapest.
It is the principle of locality that gives us a chance to overcome the long latency of memory access—and the soundness of this strategy is demonstrated at all levels of the memory hierarchy. Although these levels of the hierarchy look quite different in quantitative terms, they follow similar strategies in their operation and exploit the same properties of locality.

Multilevel caches make it possible to use more cache optimizations more easily for two reasons. First, the design parameters of a lower-level cache are different from a first-level cache. For example, because a lower-level cache will be much larger, it is possible to use larger block sizes. Second, a lower-level cache is not constantly being used by the processor, as a first-level cache is. This allows us to consider having the lower-level cache do something when it is idle that may be useful in preventing future misses.
Another trend is to seek software help. Efficiently managing the memory hierarchy using a variety of program transformations and hardware facilities is a major focus of compiler enhancements. Two different ideas are being explored. One idea is to reorganize the program to enhance its spatial and temporal locality. This approach focuses on loop-oriented programs that use large arrays as the major data structure; large linear algebra problems are a typical example, such as DGEMM. By restructuring the loops that access the arrays, substantially improved locality—and, therefore, cache performance—can be obtained.
Another approach is prefetching. In prefetching, a block of data is brought into the cache before it is actually referenced. Many microprocessors use hardware prefetching to try to predict accesses that may be difficult for software to notice.

prefetching
A technique in which data blocks needed in the future are brought into the cache early by the use of special instructions that specify the address of the block.
A third approach is special cache-aware instructions that optimize memory transfer. For example, the microprocessors in Section 6.10 in Chapter 6 use an optimization that does not fetch the contents of a block from memory on a write miss because the program is going to write the full block. This optimization significantly reduces memory traffic for one kernel.
As we will see in Chapter 6, memory systems are a central design issue for parallel processors. The growing importance of the memory hierarchy in determining system performance means that this important area will continue to be a focus for both designers and researchers for some years to come.
 Historical Perspective and Further Reading
Historical Perspective and Further Reading
This section, which appears online, gives an overview of memory technologies, from mercury delay lines to DRAM, the invention of the memory hierarchy, protection mechanisms, and virtual machines, and concludes with a brief history of operating systems, including CTSS, MULTICS, UNIX, BSD UNIX, MS-DOS, Windows, and Linux.
5.18 Exercises
5.1 In this exercise we look at memory locality properties of matrix computation. The following code is written in C, where elements within the same row are stored contiguously. Assume each word is a 32-bit integer.
for (I=0; I<8; I++)
for (J=0; J<8000; J++)
A[I][J]=B[I][0]+A[J][I];
5.1.1 [5] <§5.1> How many 32-bit integers can be stored in a 16-byte cache block?
5.1.2 [5] <§5.1> References to which variables exhibit temporal locality?
5.1.3 [5] <§5.1> References to which variables exhibit spatial locality?
Locality is affected by both the reference order and data layout. The same computation can also be written below in Matlab, which differs from C by storing matrix elements within the same column contiguously in memory.

5.1.4 [10] <§5.1> How many 16-byte cache blocks are needed to store all 32-bit matrix elements being referenced?
5.1.5 [5] <§5.1> References to which variables exhibit temporal locality?
5.1.6 [5] <§5.1> References to which variables exhibit spatial locality?
5.2 Caches are important to providing a high-performance memory hierarchy to processors. Below is a list of 32-bit memory address references, given as word addresses.
3, 180, 43, 2, 191, 88, 190, 14, 181, 44, 186, 253
5.2.1 [10] <§5.3> For each of these references, identify the binary address, the tag, and the index given a direct-mapped cache with 16 one-word blocks. Also list if each reference is a hit or a miss, assuming the cache is initially empty.
5.2.2 [10] <§5.3> For each of these references, identify the binary address, the tag, and the index given a direct-mapped cache with two-word blocks and a total size of 8 blocks. Also list if each reference is a hit or a miss, assuming the cache is initially empty.
5.2.3 [20] <§§5.3, 5.4> You are asked to optimize a cache design for the given references. There are three direct-mapped cache designs possible, all with a total of 8 words of data: C1 has 1-word blocks, C2 has 2-word blocks, and C3 has 4-word blocks. In terms of miss rate, which cache design is the best? If the miss stall time is 25 cycles, and C1 has an access time of 2 cycles, C2 takes 3 cycles, and C3 takes 5 cycles, which is the best cache design?
There are many different design parameters that are important to a cache’s overall performance. Below are listed parameters for different direct-mapped cache designs.
Cache Data Size: 32 KiB
Cache Block Size: 2 words
Cache Access Time: 1 cycle
5.2.4 [15] <§5.3> Calculate the total number of bits required for the cache listed above, assuming a 32-bit address. Given that total size, find the total size of the closest direct-mapped cache with 16-word blocks of equal size or greater. Explain why the second cache, despite its larger data size, might provide slower performance than the first cache.
5.2.5 [20] <§§5.3, 5.4> Generate a series of read requests that have a lower miss rate on a 2 KB 2-way set associative cache than the cache listed. Identify one possible solution that would make the cache listed have an equal or lower miss rate than the 2 KiB cache. Discuss the advantages and disadvantages of such a solution.
5.2.6 [15] <§5.3> The formula shown in Section 5.3 shows the typical method to index a direct-mapped cache, specifically (Block address) modulo (Number of blocks in the cache). Assuming a 32-bit address and 1024 blocks in the cache, consider a different indexing function, specifically (Block address[31:27] XOR Block address[26:22]). Is it possible to use this to index a direct-mapped cache? If so, explain why and discuss any changes that might need to be made to the cache. If it is not possible, explain why.
5.3 For a direct-mapped cache design with a 32-bit address, the following bits of the address are used to access the cache.
|
Tag |
Index |
Offset |
|
31–10 |
9–5 |
4–0 |
5.3.1 [5] <§5.3> What is the cache block size (in words)?
5.3.2 [5] <§5.3> How many entries does the cache have?
5.3.3 [5] <§5.3> What is the ratio between total bits required for such a cache implementation over the data storage bits?
Starting from power on, the following byte-addressed cache references are recorded.
![]()
5.3.4 [10] <§5.3> How many blocks are replaced?
5.3.5 [10] <§5.3> What is the hit ratio?
5.3.6 [20] <§5.3> List the final state of the cache, with each valid entry represented as a record of <index, tag, data>.
5.4 Recall that we have two write policies and write allocation policies, and their combinations can be implemented either in L1 or L2 cache. Assume the following choices for L1 and L2 caches:
|
L1 |
L2 |
|
Write through, non-write allocate |
Write back, write allocate |
5.4.1 [5] <§§5.3, 5.8> Buffers are employed between different levels of memory hierarchy to reduce access latency. For this given configuration, list the possible buffers needed between L1 and L2 caches, as well as L2 cache and memory.
5.4.2 [20] <§§5.3, 5.8> Describe the procedure of handling an L1 write-miss, considering the component involved and the possibility of replacing a dirty block.
5.4.3 [20] <§§5.3, 5.8> For a multilevel exclusive cache (a block can only reside in one of the L1 and L2 caches), configuration, describe the procedure of handling an L1 write-miss, considering the component involved and the possibility of replacing a dirty block.
Consider the following program and cache behaviors.

5.4.4 [5] <§§5.3, 5.8> For a write-through, write-allocate cache, what are the minimum read and write bandwidths (measured by byte per cycle) needed to achieve a CPI of 2?
5.4.5 [5] <§§5.3, 5.8> For a write-back, write-allocate cache, assuming 30% of replaced data cache blocks are dirty, what are the minimal read and write bandwidths needed for a CPI of 2?
5.4.6 [5] <§§5.3, 5.8> What are the minimal bandwidths needed to achieve the performance of CPI=1.5?
5.5 Media applications that play audio or video files are part of a class of workloads called “streaming” workloads; i.e., they bring in large amounts of data but do not reuse much of it. Consider a video streaming workload that accesses a 512 KiB working set sequentially with the following address stream:
0, 2, 4, 6, 8, 10, 12, 14, 16, …
5.5.1 [5] <§§5.4, 5.8> Assume a 64 KiB direct-mapped cache with a 32-byte block. What is the miss rate for the address stream above? How is this miss rate sensitive to the size of the cache or the working set? How would you categorize the misses this workload is experiencing, based on the 3C model?
5.5.2 [5] <§§5.1, 5.8> Re-compute the miss rate when the cache block size is 16 bytes, 64 bytes, and 128 bytes. What kind of locality is this workload exploiting?
5.5.3 [10] <§5.13> “Prefetching” is a technique that leverages predictable address patterns to speculatively bring in additional cache blocks when a particular cache block is accessed. One example of prefetching is a stream buffer that prefetches sequentially adjacent cache blocks into a separate buffer when a particular cache block is brought in. If the data is found in the prefetch buffer, it is considered as a hit and moved into the cache and the next cache block is prefetched. Assume a two-entry stream buffer and assume that the cache latency is such that a cache block can be loaded before the computation on the previous cache block is completed. What is the miss rate for the address stream above?
Cache block size (B) can affect both miss rate and miss latency. Assuming a 1-CPI machine with an average of 1.35 references (both instruction and data) per instruction, help find the optimal block size given the following miss rates for various block sizes.
![]()
5.5.4 [10] <§5.3> What is the optimal block size for a miss latency of 20×B cycles?
5.5.5 [10] <§5.3> What is the optimal block size for a miss latency of 24+B cycles?
5.5.6 [10] <§5.3> For constant miss latency, what is the optimal block size?
5.6 In this exercise, we will look at the different ways capacity affects overall performance. In general, cache access time is proportional to capacity. Assume that main memory accesses take 70 ns and that memory accesses are 36% of all instructions. The following table shows data for L1 caches attached to each of two processors, P1 and P2.

5.6.1 [5] <§5.4> Assuming that the L1 hit time determines the cycle times for P1 and P2, what are their respective clock rates?
5.6.2 [5] <§5.4> What is the Average Memory Access Time for P1 and P2?
5.6.3 [5] <§5.4> Assuming a base CPI of 1.0 without any memory stalls, what is the total CPI for P1 and P2? Which processor is faster?
For the next three problems, we will consider the addition of an L2 cache to P1 to presumably make up for its limited L1 cache capacity. Use the L1 cache capacities and hit times from the previous table when solving these problems. The L2 miss rate indicated is its local miss rate.
|
L2 Size |
L2 Miss Rate |
L2 Hit Time |
|
1 MB |
95% |
5.62 ns |
5.6.4 [10] <§5.4> What is the AMAT for P1 with the addition of an L2 cache? Is the AMAT better or worse with the L2 cache?
5.6.5 [5] <§5.4> Assuming a base CPI of 1.0 without any memory stalls, what is the total CPI for P1 with the addition of an L2 cache?
5.6.6 [10] <§5.4> Which processor is faster, now that P1 has an L2 cache? If P1 is faster, what miss rate would P2 need in its L1 cache to match P1’s performance? If P2 is faster, what miss rate would P1 need in its L1 cache to match P2’s performance?
5.7 This exercise examines the impact of different cache designs, specifically comparing associative caches to the direct-mapped caches from Section 5.4. For these exercises, refer to the address stream shown in Exercise 5.2.
5.7.1 [10] <§5.4> Using the sequence of references from Exercise 5.2, show the final cache contents for a three-way set associative cache with two-word blocks and a total size of 24 words. Use LRU replacement. For each reference identify the index bits, the tag bits, the block offset bits, and if it is a hit or a miss.
5.7.2 [10] <§5.4> Using the references from Exercise 5.2, show the final cache contents for a fully associative cache with one-word blocks and a total size of 8 words. Use LRU replacement. For each reference identify the index bits, the tag bits, and if it is a hit or a miss.
5.7.3 [15] <§5.4> Using the references from Exercise 5.2, what is the miss rate for a fully associative cache with two-word blocks and a total size of 8 words, using LRU replacement? What is the miss rate using MRU (most recently used) replacement? Finally what is the best possible miss rate for this cache, given any replacement policy?
Multilevel caching is an important technique to overcome the limited amount of space that a first level cache can provide while still maintaining its speed. Consider a processor with the following parameters:
5.7.4 [10] <§5.4> Calculate the CPI for the processor in the table using: 1) only a first level cache, 2) a second level direct-mapped cache, and 3) a second level eight-way set associative cache. How do these numbers change if main memory access time is doubled? If it is cut in half?
5.7.5 [10] <§5.4> It is possible to have an even greater cache hierarchy than two levels. Given the processor above with a second level, direct-mapped cache, a designer wants to add a third level cache that takes 50 cycles to access and will reduce the global miss rate to 1.3%. Would this provide better performance? In general, what are the advantages and disadvantages of adding a third level cache?
5.7.6 [20] <§5.4> In older processors such as the Intel Pentium or Alpha 21264, the second level of cache was external (located on a different chip) from the main processor and the first level cache. While this allowed for large second level caches, the latency to access the cache was much higher, and the bandwidth was typically lower because the second level cache ran at a lower frequency. Assume a 512 KB off-chip second level cache has a global miss rate of 4%. If each additional 512 KB of cache lowered global miss rates by 0.7%, and the cache had a total access time of 50 cycles, how big would the cache have to be to match the performance of the second level direct-mapped cache listed above? Of the eight-way set associative cache?
5.8 Mean Time Between Failures (MTBF), Mean Time To Replacement (MTTR), and Mean Time To Failure (MTTF) are useful metrics for evaluating the reliability and availability of a storage resource. Explore these concepts by answering the questions about devices with the following metrics.
|
MTTF |
MTTR |
|
3 Years |
1 Day |
5.8.1 [5] <§5.5> Calculate the MTBF for each of the devices in the table.
5.8.2 [5] <§5.5> Calculate the availability for each of the devices in the table.
5.8.3 [5] <§5.5> What happens to availability as the MTTR approaches 0? Is this a realistic situation?
5.8.4 [5] <§5.5> What happens to availability as the MTTR gets very high, i.e., a device is difficult to repair? Does this imply the device has low availability?
5.9 The Exercise examines the single error correcting, double error detecting (SEC/DED) Hamming code.
5.9.1 [5] <§5.5> What is the minimum number of parity bits required to protect a 128-bit word using the SEC/DED code?
5.9.2 [5] <§5.5> Section 5.5 states that modern server memory modules (DIMMs) employ SEC/DED ECC to protect each 64 bits with 8 parity bits. Compute the cost/performance ratio of this code to the code from 5.9.1. In this case, cost is the relative number of parity bits needed while performance is the relative number of errors that can be corrected. Which is better?
5.9.3 Consider a SEC code that protects 8 bit words with 4 parity bits. If we read the value 0×375, is there an error? If so, correct the error.
5.10 For a high-performance system such as a B-tree index for a database, the page size is determined mainly by the data size and disk performance. Assume that on average a B-tree index page is 70% full with fix-sized entries. The utility of a page is its B-tree depth, calculated as log2(entries). The following table shows that for 16-byte entries, and a 10-year-old disk with a 10 ms latency and 10 MB/s transfer rate, the optimal page size is 16 K.
5.10.1 [10] <§5.7> What is the best page size if entries now become 128 bytes?
5.10.2 [10] <§5.7> Based on 5.10.1, what is the best page size if pages are half full?
5.10.3 [20] <§5.7> Based on 5.10.2, what is the best page size if using a modern disk with a 3 ms latency and 100 MB/s transfer rate? Explain why future servers are likely to have larger pages.
Keeping “frequently used” (or “hot”) pages in DRAM can save disk accesses, but how do we determine the exact meaning of “frequently used” for a given system? Data engineers use the cost ratio between DRAM and disk access to quantify the reuse time threshold for hot pages. The cost of a disk access is $Disk/accesses_per_sec, while the cost to keep a page in DRAM is $DRAM_MB/page_size. The typical DRAM and disk costs and typical database page sizes at several time points are listed below:

5.10.4 [10] <§§5.1, 5.7> What are the reuse time thresholds for these three technology generations?
5.10.5 [10] <§5.7> What are the reuse time thresholds if we keep using the same 4 K page size? What’s the trend here?
5.10.6 [20] <§5.7> What other factors can be changed to keep using the same page size (thus avoiding software rewrite)? Discuss their likeliness with current technology and cost trends.
5.11 As described in Section 5.7, virtual memory uses a page table to track the mapping of virtual addresses to physical addresses. This exercise shows how this table must be updated as addresses are accessed. The following data constitutes a stream of virtual addresses as seen on a system. Assume 4 KiB pages, a 4-entry fully associative TLB, and true LRU replacement. If pages must be brought in from disk, increment the next largest page number.
4669, 2227, 13916, 34587, 48870, 12608, 49225
TLB
|
Valid |
Tag |
Physical Page Number |
|
1 |
11 |
12 |
|
1 |
7 |
4 |
|
1 |
3 |
6 |
|
0 |
4 |
9 |
Page table
|
Valid |
Physical Page or in Disk |
|
1 |
5 |
|
0 |
Disk |
|
0 |
Disk |
|
1 |
6 |
|
1 |
9 |
|
1 |
11 |
|
0 |
Disk |
|
1 |
4 |
|
0 |
Disk |
|
0 |
Disk |
|
1 |
3 |
|
1 |
12 |
5.11.1 [10] <§5.7> Given the address stream shown, and the initial TLB and page table states provided above, show the final state of the system. Also list for each reference if it is a hit in the TLB, a hit in the page table, or a page fault.
5.11.2 [15] <§5.7> Repeat part 5.11.1, but this time use 16 KiB pages instead of 4 KiB pages. What would be some of the advantages of having a larger page size? What are some of the disadvantages?
5.11.3 [15] <§§5.4, 5.7> Show the final contents of the TLB if it is 2-way set associative. Also show the contents of the TLB if it is direct mapped. Discuss the importance of having a TLB to high performance. How would virtual memory accesses be handled if there were no TLB?
There are several parameters that impact the overall size of the page table. Listed below are key page table parameters.
|
Virtual Address Size |
Page Size |
Page Table Entry Size |
|
32 bits |
8 KB |
4 bytes |
5.11.4 [5] <§5.7> Given the parameters shown above, calculate the total page table size for a system running 5 applications that utilize half of the memory available.
5.11.5 [10] <§5.7> Given the parameters shown above, calculate the total page table size for a system running 5 applications that utilize half of the memory available, given a two level page table approach with 256 entries. Assume each entry of the main page table is 6 bytes. Calculate the minimum and maximum amount of memory required.
5.11.6 [10] <§5.7> A cache designer wants to increase the size of a 4 KiB virtually indexed, physically tagged cache. Given the page size shown above, is it possible to make a 16 KiB direct-mapped cache, assuming 2 words per block? How would the designer increase the data size of the cache?
5.12 In this exercise, we will examine space/time optimizations for page tables. The following list provides parameters of a virtual memory system.

5.12.1 [10] <§5.7> For a single-level page table, how many page table entries (PTEs) are needed? How much physical memory is needed for storing the page table?
5.12.2 [10] <§5.7> Using a multilevel page table can reduce the physical memory consumption of page tables, by only keeping active PTEs in physical memory. How many levels of page tables will be needed in this case? And how many memory references are needed for address translation if missing in TLB?
5.12.3 [15] <§5.7> An inverted page table can be used to further optimize space and time. How many PTEs are needed to store the page table? Assuming a hash table implementation, what are the common case and worst case numbers of memory references needed for servicing a TLB miss?
The following table shows the contents of a 4-entry TLB.

5.12.4 [5] <§5.7> Under what scenarios would entry 2’s valid bit be set to zero?
5.12.5 [5] <§5.7> What happens when an instruction writes to VA page 30? When would a software managed TLB be faster than a hardware managed TLB?
5.12.6 [5] <§5.7> What happens when an instruction writes to VA page 200?
5.13 In this exercise, we will examine how replacement policies impact miss rate. Assume a 2-way set associative cache with 4 blocks. To solve the problems in this exercise, you may find it helpful to draw a table like the one below, as demonstrated for the address sequence “0, 1, 2, 3, 4.”
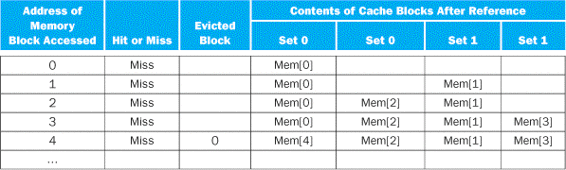
Consider the following address sequence: 0, 2, 4, 8, 10, 12, 14, 16, 0
5.13.1 [5] <§5.4, 5.8> Assuming an LRU replacement policy, how many hits does this address sequence exhibit?
5.13.2 [5] <§5.4, 5.8> Assuming an MRU (most recently used) replacement policy, how many hits does this address sequence exhibit?
5.13.3 [5] <§5.4, 5.8> Simulate a random replacement policy by flipping a coin. For example, “heads” means to evict the first block in a set and “tails” means to evict the second block in a set. How many hits does this address sequence exhibit?
5.13.4 [10] <§5.4, 5.8> Which address should be evicted at each replacement to maximize the number of hits? How many hits does this address sequence exhibit if you follow this “optimal” policy?
5.13.5 [10] <§5.4, 5.8> Describe why it is difficult to implement a cache replacement policy that is optimal for all address sequences.
5.13.6 [10] <§5.4, 5.8> Assume you could make a decision upon each memory reference whether or not you want the requested address to be cached. What impact could this have on miss rate?
5.14 To support multiple virtual machines, two levels of memory virtualization are needed. Each virtual machine still controls the mapping of virtual address (VA) to physical address (PA), while the hypervisor maps the physical address (PA) of each virtual machine to the actual machine address (MA). To accelerate such mappings, a software approach called “shadow paging” duplicates each virtual machine’s page tables in the hypervisor, and intercepts VA to PA mapping changes to keep both copies consistent. To remove the complexity of shadow page tables, a hardware approach called nested page table (NPT) explicitly supports two classes of page tables (VA ⇒ PA and PA ⇒ MA) and can walk such tables purely in hardware.
Consider the following sequence of operations: (1) Create process; (2) TLB miss; (3) page fault; (4) context switch;
5.14.1 [10] <§5.6, 5.7> What would happen for the given operation sequence for shadow page table and nested page table, respectively?
5.14.2 [10] <§5.6, 5.7> Assuming an x86-based 4-level page table in both guest and nested page table, how many memory references are needed to service a TLB miss for native vs. nested page table?
5.14.3 [15] <§5.6, 5.7> Among TLB miss rate, TLB miss latency, page fault rate, and page fault handler latency, which metrics are more important for shadow page table? Which are important for nested page table?
Assume the following parameters for a shadow paging system.

5.14.4 [10] <§5.6> For a benchmark with native execution CPI of 1, what are the CPI numbers if using shadow page tables vs. NPT (assuming only page table virtualization overhead)?
5.14.5 [10] <§5.6> What techniques can be used to reduce page table shadowing induced overhead?
5.14.6 [10] <§5.6> What techniques can be used to reduce NPT induced overhead?
5.15 One of the biggest impediments to widespread use of virtual machines is the performance overhead incurred by running a virtual machine. Listed below are various performance parameters and application behavior.

5.15.1 [10] <§5.6> Calculate the CPI for the system listed above assuming that there are no accesses to I/O. What is the CPI if the VMM performance impact doubles? If it is cut in half? If a virtual machine software company wishes to obtain a 10% performance degradation, what is the longest possible penalty to trap to the VMM?
5.15.2 [10] <§5.6> I/O accesses often have a large impact on overall system performance. Calculate the CPI of a machine using the performance characteristics above, assuming a non-virtualized system. Calculate the CPI again, this time using a virtualized system. How do these CPIs change if the system has half the I/O accesses? Explain why I/O bound applications have a smaller impact from virtualization.
5.15.3 [30] <§5.6, 5.7> Compare and contrast the ideas of virtual memory and virtual machines. How do the goals of each compare? What are the pros and cons of each? List a few cases where virtual memory is desired, and a few cases where virtual machines are desired.
5.15.4 [20] <§5.6> Section 5.6 discusses virtualization under the assumption that the virtualized system is running the same ISA as the underlying hardware. However, one possible use of virtualization is to emulate non-native ISAs. An example of this is QEMU, which emulates a variety of ISAs such as MIPS, SPARC, and PowerPC. What are some of the difficulties involved in this kind of virtualization? Is it possible for an emulated system to run faster than on its native ISA?
5.16 In this exercise, we will explore the control unit for a cache controller for a processor with a write buffer. Use the finite state machine found in Figure 5.40 as a starting point for designing your own finite state machines. Assume that the cache controller is for the simple direct-mapped cache described on page 465 (Figure 5.40 in Section 5.9), but you will add a write buffer with a capacity of one block.
Recall that the purpose of a write buffer is to serve as temporary storage so that the processor doesn’t have to wait for two memory accesses on a dirty miss. Rather than writing back the dirty block before reading the new block, it buffers the dirty block and immediately begins reading the new block. The dirty block can then be written to main memory while the processor is working.
5.16.1 [10] <§5.8, 5.9> What should happen if the processor issues a request that hits in the cache while a block is being written back to main memory from the write buffer?
5.16.2 [10] <§5.8, 5.9> What should happen if the processor issues a request that misses in the cache while a block is being written back to main memory from the write buffer?
5.16.3 [30] <§5.8, 5.9> Design a finite state machine to enable the use of a write buffer.
5.17 Cache coherence concerns the views of multiple processors on a given cache block. The following data shows two processors and their read/write operations on two different words of a cache block X (initially X[0]=X[1]=0). Assume the size of integers is 32 bits.
|
P1 |
P2 |
|
X[0] ++; X[1] = 3; |
X[0] = 5; X[1] +=2; |
5.17.1 [15] <§5.10> List the possible values of the given cache block for a correct cache coherence protocol implementation. List at least one more possible value of the block if the protocol doesn’t ensure cache coherency.
5.17.2 [15] <§5.10> For a snooping protocol, list a valid operation sequence on each processor/cache to finish the above read/write operations.
5.17.3 [10] <§5.10> What are the best-case and worst-case numbers of cache misses needed to execute the listed read/write instructions?
Memory consistency concerns the views of multiple data items. The following data shows two processors and their read/write operations on different cache blocks (A and B initially 0).
|
P1 |
P2 |
|
A = 1; B = 2; A+=2; B++; |
C = B; D = A; |
5.17.4 [15] <§5.10> List the possible values of C and D for an implementation that ensures both consistency assumptions on page 470.
5.17.5 [15] <§5.10> List at least one more possible pair of values for C and D if such assumptions are not maintained.
5.17.6 [15] <§§5.3, 5.10> For various combinations of write policies and write allocation policies, which combinations make the protocol implementation simpler?
5.18 Chip multiprocessors (CMPs) have multiple cores and their caches on a single chip. CMP on-chip L2 cache design has interesting trade-offs. The following table shows the miss rates and hit latencies for two benchmarks with private vs. shared L2 cache designs. Assume L1 cache misses once every 32 instructions.
|
Private |
Shared |
|
|
Benchmark A misses-per-instruction |
0.30% |
0.12% |
|
Benchmark B misses-per-instruction |
0.06% |
0.03% |
Assume the following hit latencies:
|
Private Cache |
Shared Cache |
Memory |
|
5 |
20 |
180 |
5.18.1 [15] <§5.13> Which cache design is better for each of these benchmarks? Use data to support your conclusion.
5.18.2 [15] <§5.13> Shared cache latency increases with the CMP size. Choose the best design if the shared cache latency doubles. Off-chip bandwidth becomes the bottleneck as the number of CMP cores increases. Choose the best design if off-chip memory latency doubles.
5.18.3 [10] <§5.13> Discuss the pros and cons of shared vs. private L2 caches for both single-threaded, multi-threaded, and multiprogrammed workloads, and reconsider them if having on-chip L3 caches.
5.18.4 [15] <§5.13> Assume both benchmarks have a base CPI of 1 (ideal L2 cache). If having nonblocking cache improves the average number of concurrent L2 misses from 1 to 2, how much performance improvement does this provide over a shared L2 cache? How much improvement can be achieved over private L2?
5.18.5 [10] <§5.13> Assume new generations of processors double the number of cores every 18 months. To maintain the same level of per-core performance, how much more off-chip memory bandwidth is needed for a processor released in three years?
5.18.6 [15] <§5.13> Consider the entire memory hierarchy. What kinds of optimizations can improve the number of concurrent misses?
5.19 In this exercise we show the definition of a web server log and examine code optimizations to improve log processing speed. The data structure for the log is defined as follows:

Assume the following processing function for the log:
topK_sourceIP (int hour);
5.19.1 [5] <§5.15> Which fields in a log entry will be accessed for the given log processing function? Assuming 64-byte cache blocks and no prefetching, how many cache misses per entry does the given function incur on average?
5.19.2 [10] <§5.15> How can you reorganize the data structure to improve cache utilization and access locality? Show your structure definition code.
5.19.3 [10] <§5.15> Give an example of another log processing function that would prefer a different data structure layout. If both functions are important, how would you rewrite the program to improve the overall performance? Supplement the discussion with code snippet and data.
For the problems below, use data from “Cache Performance for SPEC CPU2000 Benchmarks” (http://www.cs.wisc.edu/multifacet/misc/spec2000cache-data/) for the pairs of benchmarks shown in the following table.
|
a. |
Mesa / gcc |
|
b. |
mcf / swim |
5.19.4 [10] <§5.15> For 64 KiB data caches with varying set associativities, what are the miss rates broken down by miss types (cold, capacity, and conflict misses) for each benchmark?
5.19.5 [10] <§5.15> Select the set associativity to be used by a 64 KiB L1 data cache shared by both benchmarks. If the L1 cache has to be directly mapped, select the set associativity for the 1 MiB L2 cache.
5.19.6 [20] <§5.15> Give an example in the miss rate table where higher set associativity actually increases miss rate. Construct a cache configuration and reference stream to demonstrate this.