Biologically Inspired Computer Vision (2015)

Part III
Modelling

Chapter 10
From Neuronal Models to Neuronal Dynamics and Image Processing

Matthias S. Keil

10.1 Introduction

Neurons make contacts with each other through synapses: the presynaptic neuron sends its output to the synapse via an axon and the postsynaptic neuron receives it via its dendritic tree (“dendrite”). Most neurons produce their output in the form of virtually binary events (action potentials or spikes). Some classes of neurons (e.g., in the retina) nevertheless do not generate spikes but show continuous responses. Dendrites were classically considered as passive cables whose only function is to transmit input signals to the soma (the cell body of the neuron). In this picture, a neuron integrates all input signals and generates a response if their sum exceeds a threshold. Therefore, the neuron is the site where computations take place, and information is stored across the network in synaptic weights (“connection strengths”). This “connectionist” point of view on neuronal functioning inspired neuronal networks learning algorithms such as error backpropagation [1], and the more recent deep-learning architectures [2]. Recent evidence, however, suggest that dendrites are excitable structures rather than passive cables, which can perform sophisticated computations [3–6]. This suggests that even single neurons can carry out far more complex computations than previously thought.

Naturally, a modeler has to choose a reasonable level of abstraction. A good model is not necessarily one which incorporates all possible details, because too many details can make it difficult to identify important mechanisms. The level of detail is related to the research question that we wish to answer, but also to our computational resources [7]. For example, if our interest was to understanding the neurophysiological details of a small circuit of neurons, then we probably would choose a Hodgkin–Huxley model for each neuron [8] and also include detailed models of dendrites, axons, and synaptic dynamic and learning. A disadvantage of the Hodgkin–Huxleymodel is its high computational complexity. It requires about floating point operations (FLOPS) for the simulation of ms of time [9].

Therefore, if we want to simulate a large network with many neurons, then we may omit dendrites and axons, and use a simpler model such as the integrate-and-fire neuron model (which is presented in the following) or the Izhikevich model [10]. The Izhikevich model offers the same rich spiking dynamics as the full Hodgkin–Huxley model (e.g., bursting, tonic spiking), while having a computational complexity similar to the integrate-and-fire neuron model (about and FLOPS ms, respectively). Further simplifications can be made if we aim at simulating psychophysical data, or at solving image processing tasks. For example, spiking mechanisms are often not necessary then, and we can compute a continuous response (as opposed to binary spikes) from the neuron's state variable (e.g., membrane potential) by thresholding (half-wave rectification, e.g., ) or via a sigmoidal function (“squashing function”, e.g., ).

This chapter approaches neural modeling and computational neuroscience, respectively, in a tutorial-like fashion. This means that basic concepts are explained by way of simple examples, rather than providing an in-depth review on a specific topic. We proceed by first introducing a simple neuron model (the membrane potential equation), which is derived by considering a neuron as an electrical circuit. When the membrane potential equation is augmented with a spiking mechanism, it is known as the leaky integrate-and-fire model. “Leaky” means that the model forgets exponentially fast about past inputs. “Integrate” means that it sums its inputs, which can be excitatory (driving the neuron toward its response threshold) or inhibitory (drawing the state variable away from the response threshold). Finally, “fire” refers to the spiking mechanism.

The membrane potential equation is subsequently applied to three image processing tasks. Section 10.3 presents a reaction-diffusion-based model of the retina, which accounts for simple visual illusions and afterimages. Section 10.4 describes a model for segregating texture features that is inspired by computations in the primary visual cortex [11]. Finally, Section 10.5 introduces a model of a collision-sensitive neuron in the locust visual system [12]. The last section discusses a few examples where image processing (or computer vision) methods also could explain how the brain processes the corresponding information.

10.2 The Membrane Equation as a Neuron Model

In order to derive a simple yet powerful neuron model, imagine the neuron's cellmembrane (comprising dendrites, soma, and axon) as a small sphere. The membrane is a bilayer of lipids, which is – Å thick ( Å m nm). It isolates the extracellular space from a cell's interior and thus forms a barrier for different ion species, such as Na⁺ (sodium), K⁺ (potassium), and (chloride). Now if the ionic concentrations in the extracellular fluid and the cytoplasm (the cell's interior) were all the same, then one would be probably dead. Neuronal signaling relies on the presence of ionic gradients. With all cells at rest (i.e., neither input nor output), about half of the brain's energy budget is consumed for moving Na⁺ to the outside of the cell and K⁺ inward (the – pump). Some types of neurons also pump outside (via the transporter). The pumping mechanisms compensate for the ions that leak through the cell membrane in the respective reverse directions, driven by electrochemical gradients. At rest, the neuron therefore maintains a dynamic equilibrium.

We are now ready to model the neuron as an electrical circuit, where a capacitance (cell membrane) is connected in parallel with a (serially connected) resistance and a battery. The battery sets the cell's resting potential . In particular, all (neuron-, glia-, muscle-) cells have a negative resting potential, typically mV. The resting potential is the value of the membrane voltage when all ionic concentrations are in their dynamic equilibrium. This is, of course, a simplification because we lump together the diffusion potentials (such as or ) of each ion species. The simplification comes at a cost, however, and our resulting neuron model will not be able to produce action potentials or spikes by itself (the binary events by which many neurons communicate with each other) without explicitly adding a spike-generating mechanism (more on that in Section 10.2.2). By Ohm's law, the current that leaks through the membrane is , where the leakage conductance is just the inverse of the membrane resistance. The charge which is kept apart by a cell's membrane with capacitance is . Whenever the neuron signals, the distribution of charges changes, and so does the membrane potential, and thus will be nonzero. In other words, a current will flow, carried by ions. Assuming some fixed value for , the change in will be slower for a higher capacitance (better buffering capacity). Kirchhoff's current law is the equivalent of current conservation , or

10.1

The right-hand side corresponds to current flows due to excitation and inhibition (this is discussed later in the following). Biologically, current flows occur across protein molecules that are embedded in the cell membrane. The various protein types implement specific functions such as ionic channels, enzymes, pumps, and receptors. These “gates” or “doors” through the cell membrane are highly specific, such that only particular information or substances (such as ions) can enter or exit the cell. Strictly speaking, each channel which is embedded in a neuron's cell membrane would correspond to an RC-circuit ( is the resistance, is the capacitance) such as Eq. (10.1). But fortunately, neurons are very small – this is what justifies the assumption that channels are uniformly distributed – and the potential does not vary across the cell membrane: The cell is said to be isopotential, and it can be adequately described by a single RC-compartment.

Let us assume that we have nothing better to do than waiting for a sufficiently long time such that the neuron reaches equilibrium. Then, by definition, is constant, and thus . What remains from the last equation is just , or . In the absence of excitation and inhibition, we have and the neuron will be at its resting potential. But how long do we have to wait until equilibrium is reached? To find this out, we just move all terms with to one side of the equation, and the term which contains time to the other. This technique is known as separation of variables, and permits integration in order to convert the infinitesimal quantities and into “normal” variables (we formally rename the corresponding integration variables for time and voltage as and , respectively),

10.2

where . We further define . Integration of the left-hand side gives . With the (membrane) time constant of the cell , the above equation yields

10.3

It is easy to see that for we get , where in the absence of external currents (this confirms our previous result). The time that we have to wait until this equilibrium is reached depends on : The higher the resistance , and the bigger the capacitance , the longer it will take (and vice versa).

The constant has to be selected according to the initial conditions of the problem. For example, if we assume that the neuron is at rest when we start the simulation, then , and therefore

10.4

10.2.1 Synaptic Inputs

Neurons are not loners but are massively connected to other neurons. The connection sites are called synapses. Synapses come in two flavors: electrical and chemical. Electrical synapses (also called gap junctions) can directly couple the membrane potential of neighboring neurons. In this way, distinct networks of specific neurons are formed, usually between neurons of the same type. Examples of electrically coupled neurons are retinal horizontal cells [13, 14], cortical low-threshold-spiking interneurons, and cortical fast-spiking interneurons [15, 16] (interneurons are inhibitory). Sometimes chemical and electrical synapses even combine to permit reliable and fast signal transmission, such as it is the case in the locust, where the lobula giant movement detector (LGMD ) connects to the descending contralateral movement detector (DMCD ) [17–20].

Chemical synapses are far more common than gap junctions. In one cubic millimeter of cortical gray matter, there are about one billion () chemical synapses (about in the whole human brain). Synapses are usually plastic. Whether they increase or decrease their connection strength to a postsynaptic neuron depends on causality. If a presynaptic neuron fires within some 5–40 ms before the postsynaptic neuron, the connection gets stronger (potentiation: “P”) [21]. In contrast, if the presynaptic spike arrives after activation of the postsynaptic neuron, synaptic strength is decreased (depression: “D”) [22]. This mechanism is known as spike-time-dependent plasticity (STDP), and can be identified with Hebbian learning [23, 24]. Synaptic potentiation is thought to be triggered by backpropagating calcium spikes in the dendrites of postsynaptic neuron [25] Synaptic plasticity can occur over several timescales, short term (ST) and long term (LT). Remember these acronyms if you see letter combinations such as “LTD,” “LTP,” “STP,” or “STD”.

An activation of fast, chemical synapses causes a rapid and transient voltage change in the postsynaptic neuron. These voltage changes are called postsynaptic potentials (PSPs). PSPs can be either inhibitory (IPSPs) or excitatory (EPSPs). Excitatory neurons depolarize their target neurons ( will get more positive as a consequence of the EPSP), whereas inhibitory neurons hyperpolarize their postsynaptic targets. How can we model synapses? PSPs are caused by a temporary increase in membrane conductance in series with a so-called synaptic reversal battery (also synaptic reversal potential, or synaptic battery). The synaptic input defines the current on the right-hand side of Eq. (10.1),

10.5

The last equation sums synaptic inputs, each with conductance and reversal potential . Notice that whether an input acts excitatory or inhibitory on the membrane potential depends usually on whether the synaptic battery is bigger or smaller than the resting potential . Just consider only one type of excitatory and inhibitory input. Then we can write

10.6

(for all simulations, if not otherwise stated, we assume and omit the physical units). How do we solve this equation? After converting the differential equation into a difference equation, the equation can be solved numerically with standard integration schemes, such as Euler's method, Runge–Kutta, Crank–Nicolson, or Adams–Bashforth (see, e.g., chapter 6 in Ref. [26] and chapter 17 in Ref. [27] for more details). Typically, model neurons are integrated with a step size of ms or less, as this is the relevant timescale for neuronal signaling. If the simulation focuses more on perceptual dynamics (or biologically inspired image processing tasks), then one may choose a bigger integration time constant as well. The ideal integration method is stable, produces solutions with a high accuracy, and has a low computational complexity. In practice, of course, we have to make the one or the other trade-off.

Remember that is called leakage conductance, which is just the inverse of the membrane resistance. For constant capacitance , the leakage conductance determines the time constant of the neuron: bigger values of will make it “faster” (i.e., less memory on past inputs), while smaller values will cause a higherdegree of lowpass filtering of the input. and are the excitatory and inhibitory synaptic batteries, respectively.

For the synaptic current (mainly and ) is inward and negative by convention. The membrane thus gets depolarized. This is a signature of an EPSP. In the brain, the most common type of excitatory synapses release glutamate (a neurotransmitter).¹ The neurotransmitter diffuses across the synaptic cleft, and binds on glutamate-sensitive receptors in the postsynaptic cell membrane. As a consequence, ion channels will open, and and (and also via voltage sensitive channels) will enter the cell.

Agonists are pharmacological substances that do not exist in the brain, but open these channels as well. For instance, the agonist NMDA² will open excitatory, voltage-sensitive NMDA-channels. AMPA³ is another agonist that activates fast excitatory synapses. However, AMPA-synapses will remain silent in the presence of NMDA, and vice versa. Therefore one can imagine the ionic channels as locked doors. For their opening, the right key is necessary, which is either a specific neurotransmitter, or some “artificial” pharmacological agonist. The “locks” are the receptor sites to which a neurotransmitter or an agonist binds. The reversal potentials of the fast AMPA-synapse is about 80–100 mV above the resting potential. Usually, AMPA-channels co-occur with NMDA-channels, and this may enhance the computational power of a neuron [28].

For the membrane is hyperpolarized. For , it gets less sensitive to depolarization, and accelerates the return to for any synaptic input. Presynaptic release of GABA⁴ can activate three subtypes of receptors: GABA, GABA, and GABA (as before, they are identified through the action of specific pharmalogicals)⁵

Why are the synaptic batteries also called reversal potentials ? For excitatory input, imposes an upper limit on . This means that no matter how big will be, it can drive the neuron only up to . In order to understand this, consider , the so-called driving potential: if , then the driving potential is high, and the neuron depolarizes fast. The closer gets to , the smaller the driving potential, until the excitatory current eventually approaches zero. (Analog considerations hold for the inhibitory input).

What is the value of at equilibrium? Equilibrium means that does not change with , and then the left hand side of Eq. (10.6) iszero. Of course this implies that all excitatory and inhibitory inputs vary sufficiently slowly and we can consider them as being constant. Otherwise expressed, the neuron reaches the equilibrium before a significant change in or takes place. Then, solving Eq. (10.6) for yields

10.7

The time until the equilibrium is reached depends not only on , but on all other active conductances. As a consequence, a neuron which receives continuous input from other neurons can react faster than a neuron which starts from [30]. (Ongoing cortical activity is the normal situation, where it is thought that excitation and inhibition are just balanced [31]).

A specially interesting case is defined by , which is called silent or shunting inhibition. It is silent because it only becomes evident if the neuron is depolarized (and hyperpolarized if more than one type of inhibition is considered). Shunting inhibition decreases the time constant of the neuron, thus making it faster. In this way, the return to the resting potential is accelerated for excitatory and inhibitory input. Furthermore, divisive inhibition is a special form of shunting inhibition if . With spiking neurons, however, pure divisive inhibition does not seem to exist. In that case, shunting inhibition is rather subtractive [32] and cannot act as a gain control mechanism. But in networks with balanced excitation and inhibition, the choice is ours: if we change the balance between excitation and inhibition, then the effect on a neuron's response will be additive and subtractive, respectively. If we leave the balance unchanged and increase or decrease excitation and inhibition in parallel, then a multiplicative or divisive effect on a neuron's response will occur [33].

10.2.2 Firing Spikes

Equation (10.6) represents the membrane potential of a neuron, but could represent different quantities as well. For example, could be interpreted directly as response probability if we set, for example, , , and . Accordingly, in the latter case we have . Another possibility is to set . As neuronal responses are only positive, however, has to be half-wave rectified, meaning that we take as the output of the neuron.⁶ Naturally, half-wave rectification makes sense only if negative values of can occur. Because of the absence of explicit spiking, the neuron's output represents a (mean) firing rate, usually interpreted as spikes per second.

When should one use Eq. (10.6) or (10.7)? This depends mainly on the purpose of the simulation. When the synaptic input consists of spikes, then one needs some mechanism to convert them into continuous quantities. The lowpass filtering characteristics of Eq. (10.6) will do that. For instance, spikes are necessary for implementing spike-time-dependent plasticity (STDP), which modifies synaptic strength dependent on pre- and postsynaptic activity. For some purposes (e.g., biologically inspired image processing), spikes are not strictly necessary, and one can use the (mean or instantaneous) firing rate (or activity, that is, the rectified membrane potential) of presynaptic neurons directly as input to postsynaptic neurons. In that case, either Eq. (10.6) or (10.7) could be used. The steady-state solution (Eq. (10.7)), however, has less computational complexity, as one does not need to integrate it numerically. Recall that when using the steady-state solution, one implicitly assumes that the synaptic input varies on a relatively slow timescale, such that the neuron can reach its equilibrium state at each instant.

It is straightforward to convert (10.6) into a leaky integrate-and-fire neuron. The term “leaky” refers to the leakage conductance , and the neuron would only be a perfect integrator for As soon as the membrane potential crosses the neuron's response threshold , we record a pulse with some amplitude in the neuron's response. Otherwise, the response is usually defined as being zero:

1 if V>Vthresh % Vthresh = response threshold

2 % response is a pulse with amplitude ‘SpikeAmp’

3 response = SpikeAmp;

4 % reset membrane potential (afterhyperpolarization)

5 V = Vreset;

6 else

7 response = 0; % else, the neuron stays silent

8 end

In order to account for afterhyperpolarization (i.e., the refractory period), is set to some value after each spike. Usually, is chosen. The refractory period of a neuron is the time that the ionic pumps need to reestablish the original ion charge distributions. Within the absolute refractory period, the neuron will not spike at all or spiking probability will be greatly reduced (relative refractory period). Other spiking mechanisms are conceivable as well. For example, we can define the model neuron's response as being identical to firing rate , and add a spike to whenever . Then would represent a spiking threshold :

1 if V>Vthresh % ‘Vthresh’ = spiking threshold

2 % add a spike with amplitude ‘SpikeAmp’ to current ...

membrane potential ‘V’

3 response = V + SpikeAmp;

4 % reset membrane potential (refractory period)

5 V = Vreset;

6 else

7 response = max(V,0); % otherwise, rate-code-like ...

response (by half-wave rectification of ‘V’)

8 end

The response thus switches between a rate code () and a spike code () [34, 35]. A typical spike train produced by the latter mechanism is shown in Figure 10.1(b).

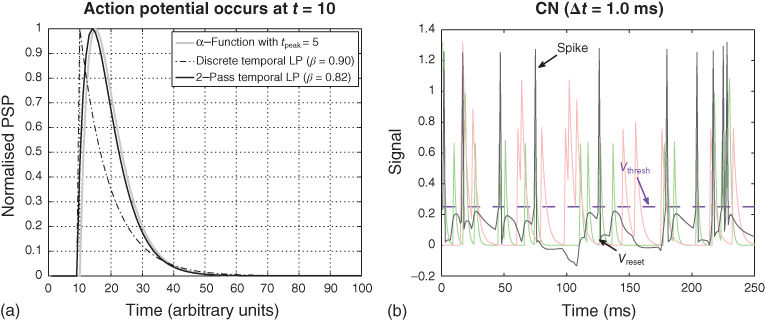
Figure 10.1 Spikes and postsynaptic potentials. (a) The figure shows three methods for converting a spike (value one at , that is ) into a postsynaptic potential (PSP). The -function with (Eq. (10.8)) is represented by the gray curve. The result of lowpass filtering the spike once (via Eq. (10.10) with ) is shown by the dashed line: The curve has a sudden rise and a gradual decay. Finally, applying two times the lowpass filter (each with ) to the spike results in the black curve. Thus, a 2-pass lowpass filter can approximate the -function reasonably well. (b) The figure shows PSPs and output of the model neuron Eq. (10.6) endowed with a spike mechanism. Excitatory (, pale green curve) and inhibitory (, pale red curve) PSPs cause corresponding fluctuations in the membrane potential (black curve). As soon as the membrane potential crosses the threshold (dashed horizontal line), a spike is added to , after which the membrane potential is reset to . The half-wave rectified membrane potential represents the neuron's output. The input to the model neuron were random spikes which were generated according to a Poisson process (with rates and spikes per second, respectively). The random spikes were converted into PSPs via simple lowpass filtering (Eq. (10.10)) with filter memories and , respectively, and weight . The integration method was Crank (not Jack)–Nicolson with step size ms. The rest of the parameters of Eq. (10.6) were , , , and .

How are binary events such as spikes converted into PSPs? A PSP has a sharp rise and a smooth decay, and therefore is usually broader than the spike by which it was evoked. Assume that a spike arrives at time at the postsynaptic neuron. Then the time course of the corresponding PSP (i.e., the excitatory or inhibitory input to the neuron) is adequately described by the so-called α-function:

10.8

The constant is chosen such that matches the desired maximum of the PSP. The Heaviside function is zero for , and otherwise. It makes sure that the PSP generated by the spike at starts at time . The total synaptic input into the neuron is , multiplied with a synaptic weight .

Instead of using the -function, we can simplify matters (and accelerate our simulation) by assuming that each spike causes an instantaneous increase in or , respectively, followed by an exponential decay. Doing so just amounts to adding one simple differential equation to our model neuron:

10.9

The time constant determines the rate of the exponential decay (faster decay if smaller), is the synaptic weight, and is the Kronecker delta function, which is just one if its argument is zero: The th spike increments by . The last equation lowpass filters the spikes. An easy-to-compute discrete version can be obtained by converting the last equation into a finite difference equation, either by forward or backward differencing (details can be found in section S8 of Ref. [36]):

10.10

For forward differentiation, , where is the integration time constant that comes from approximating by . For backward differencing, . The degree of lowpass filtering (filter memory on past inputs) is determined by . For , the filter output just reproduces the input spike pattern (the filter is said to have no memory on past inputs). For , the filter ignores any input spikes, and stays forever at the value with which it was initialized (“infinite memory”). For any value between zero and one, filtering takes place, where filtering gets stronger with increasing .

When one or more spikes are filtered by Eq. (10.10), then we see a sudden increase in at time , followed by a gradual decay (Figure 10.1(a), dashed curve). This sudden increase stands in contrast to the gradual increase of the PSP as predicted by Eq. (10.8) (Figure 10.1(a), gray curve). A better approximation to the shape of a PSP results from applying lowpass filtering twice, as shown by the black curve in Figure 10.1(a). This is tantamount to cascade two times equation (10.10) for each synaptic input Eq. (10.6).

10.3 Application 1: A Dynamical Retinal Model

The retina is a powerful computational device. It transforms light intensities of different wavelengths – as captured by cones (and rods for low-light vision) – into an efficient representation which is sent to the brain by the axons of the retinal ganglion cells [37]. The term “efficient” refers to redundancy reduction (“decorrelation”) in the stimulus on the one hand, and coding efficiency at the level of ganglion cells, on the other. Decorrelation means that predictable intensity levels in time and space are suppressed in the responses of ganglion cells [38, 39]. For example, a digital photograph of a clear blue sky has a lot of spatial redundancy, because if we select a blue pixel, it is highly probable that its neighbors are blue pixels as well [40]. Coding efficiency is linked to metabolic energy consumption. Energy consumption increases faster than information transmission capacity, and organisms therefore seem to have evolved to a trade-off between increasing their evolutionary fitness and saving energy [41]. Retinal ganglion cells show efficient coding in the sense that noisy or energetically expensive coding symbols are less “used” [37, 42]. Often, the spatial aspects of visual information processing by the retina are grossly approximated by employing the difference-of-Gaussian (“DoG”) model (one Gaussian is slightly broader than the other) [43]. The Gaussians are typically two-dimensional, isotropic, and centered at identical spatial coordinates. The resulting DoG model is a convolution kernel with positive values in the center surrounded by negative values. In mathematical terms, the DoG-kernel is a filter that takes the second derivative of an image. In signal processing terms, it is a bandpass filter (or a highpass filter if a small kernel is used). In this way, the center–surround antagonism of (foveal) retinal ganglion cells can be modeled [44]: ON-center ganglion cells respond when the center is more illuminated than the surround (i.e., positive values after convolving the DoG kernel with an image). OFF-cells respond when the surround receives more light intensity than the center (i.e., negative values after convolution). The DoG model thus assumes symmetric ON- and OFF-responses; this is again a simplification: differences between biological ON- and OFF ganglion cells include receptive field size, response kinetics, nonlinearities, and light–dark adaptation [45–47]. Naturally, convolving an image with a DoG filter can neither account for adaptation nor for dynamical aspects of retinal information processing. On the other hand, however, many retinal models which target the explanation of physiological or psychophysical data are not suitable for image processing tasks. So, biologically inspired image processing means that the model should solve an image processing task (e.g., boundary extraction, dynamic range reduction), while at the same time it should produce predictions or have features which are by andlarge consistent with psychophysics and biology (e.g., brightness illusions, kernels mimicking receptive fields). In this spirit, we now introduce a simple dynamical model for retinal processing, which reproduces some interesting brightness illusions and could even account for afterimages. An afterimage is an illusory percept where one continues to see a stimulus which is physically not present any more (e.g., a spot after looking into a bright light source). Unfortunately, the author was unable to find a version of the model which could be strictly based on Eq. (10.6). Instead of that, here is an even simpler version that is based on the temporal lowpass filter (Eq. (10.10)). Let be a gray-level image with luminance values between zero (dark) and one (white). The number of iterations is denoted by (discrete time). Then

10.11

10.12

where ON-cell responses, OFF-cell responses, is the diffusion coefficient,is the diffusion operator (Laplacian), which was discretized as a convolution kernel with in the center, and in north, east, south, and west pixels. Corner pixels were zero. Thus, whereas the receptive field center is just one pixel, the surround is dynamically constructed by diffusion. Diffusion length (and thus surround size) depends on the filter memory constant and the diffusion coefficient (bigger values will produce a larger surround area).

Figure 10.2 shows four test images which were used for testing the dynamic retina model. Figure 10.2(a) shows a visual illusion (“grating induction”), where observers perceive an illusory modulation of luminance between the two gratings, although luminance is actually constant. Figure 10.3(a) shows that the dynamic retina predicts a wavelike activity pattern within the grating via . Because ON-responses represent brightness (perceived luminance) and OFF-responses represent darkness (perceived inverse luminance) , the dynamic retina correctly predicts grating induction. Does it also account for the absence of grating induction in Figure 10.2(b)? The corresponding simulation is shown in Figure 10.3(b), where the amplitude of the wave-like pattern is strongly reduced, and the frequency has doubled. Thus, the absence of grating induction is adequately predicted.

Figure 10.2 Test images All images have rows and columns. (a) The upper and the lower grating (“ìnducers”) are separated by a small stripe, which is called the test stripe. Although the test stripe has the same luminance throughout, humans perceive a wavelike pattern with opposite brightness than the inducers, that is, where the inducers are white, the test stripe appears darker and vice versa. (b) When the inducer gratings have an opposite phase (i.e., white stands vis-á-vis black), then the illusory luminance variation across the test stripe is weak or absent. (c) A real-world image or photograph (“camera”). (d) A luminance staircase, which is used to illustrate afterimages in Figure 10.4(c) and (d).

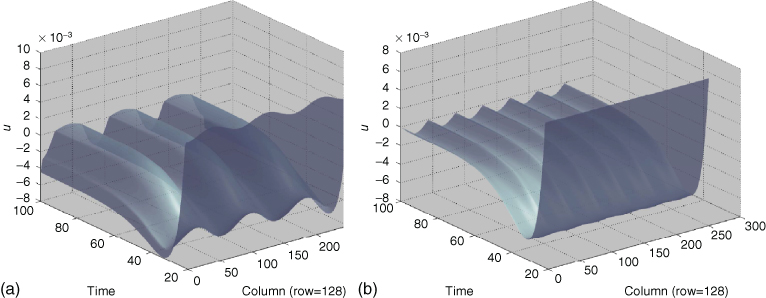
Figure 10.3 Simulation of grating induction. Does the dynamic retina (Eqs. (10.11) and (10.12)) predict the illusory luminance variation across the test stripe (the small stripe which separates the two gratings in Figure 10.2(a) and (b))? (a) Here, the image of Figure 10.2(a) was assigned to . The plot shows the temporal evolution of the horizontal line centered at the test stripe, that is, it shows all columns of for the fixed row number at different instances in time . Time increases toward the background. If values (ON-responses) are interpreted as brightness, and values (OFF-responses) as darkness, then the wave pattern adequately predicts the grating induction effect. (b) If the image of Figure 10.2(b) is assigned to (where human observers usually do not perceive grating induction), then the wavelike pattern will have twice the frequency of the inducer gratings, and moreover a strongly reduced amplitude. Thus, the dynamic retina correctly predicts a greatly reduced brightness (and darkness) modulation across the test stripe.

In its equilibrium state, the dynamic retina performs contrast enhancement or boundary detection, respectively. This is illustrated with the ON- and OFF-responses (Figure 10.4(a) and (b), respectively) to Figure 10.2(c). In comparison to an ordinary DoG-filter, however, the responses of the dynamic retina are asymmetric, with somewhat higher OFF-responses to a luminance step (not shown). A nice feature of the dynamic retina is the prediction of after images. This is illustrated by computing first the responses to a luminance staircase (Figure 10.2(d)), and then replacing the staircase image by the image of the cameraman (Figure 10.2(c)). Figure 10.4(c) and (d) shows corresponding responses immediately after the images were swapped. Although the camera man image is now assigned to , a slightly blurred afterimage of the staircase still appears in . The persistence of the afterimage depends on the luminance values: Higher intensities in the first image, and lower intensities in the second image will promote a prolonged effect.

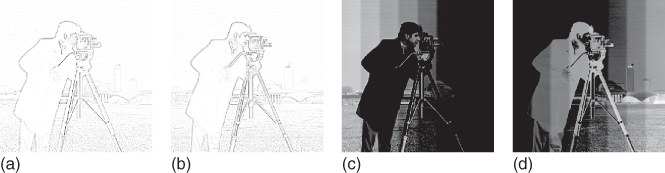
Figure 10.4 Snapshots of the dynamic retina. (a) This is the ON-response (Eq. (10.11) ) after iterations of the dynamic retina (Eqs. (10.11) and (10.12)), where the image of Figure 10.2(c) was assigned to . Darker gray levels indicate higher values of ). (b) Here the corresponding OFF-responses () are shown, where darker gray levels indicate higher OFF-responses. (c) Until , the luminance staircase (Figure 10.2(d)) was assigned to . Then the image was replaced by the image of the camera man. This simulates a retinal saccade. As a consequence, a ghost image of the luminance staircase is visible in both ON- and OFF-responses (approximately until ). From on, the ON- and OFF-responses are indistinguishable from (a) and (b). Here, brighter gray levels indicate higher values of . (d) Corresponding OFF-responses to (c). Again, brighter gray levels indicate higher values of . All simulations were performed with filter memory constants , , and diffusion coefficient .

10.4 Application 2: Texture Segregation

Networks based on Eq. (10.6) can be used for biologically plausible image processing tasks. Nevertheless, the specific task that one wishes to achieve may imply modifications of Eq. (10.6). As an example we outline a corresponding network for segregating texture from grayscale image (“texture system”). We omit many mathematical details at this point (cf. Chapter 4 in Ref. [11]), because they probably would make reading too cumbersome.

The texture system forms part of a theory for explaining early visual information processing [11]. The essential proposal is that simple cells in V1 (primary visual cortex) segregate the visual input into texture, surfaces, and (slowly varying) luminance gradients. This idea emerges quite naturally from considering how the symmetry and scale of simple cells relate to features in the visual world. Simple cells with small and odd-symmetric receptive fields (RFs) respond preferably to contours that are caused by changes in material properties of objects such as reflectance. Object surfaces are delimited by odd-symmetric contours. Likewise, even-symmetrical simple cells respond particularly well to lines and points, which we call texture in this context. Texture features are often superimposed on object surfaces. Texture features may be variable and be rather irrelevant in the recognition of a certain object (e.g., if the object is covered by grains of sand), but also may correspond to an identifying feature (e.g., tree bark). Finally, simple cells at coarse resolutions (i.e., those with big RFs of both symmetries) are supposed to detect shallow luminance gradients. Luminance gradients are a pictorial depth cue for resolving the three-dimensional layout of a visual scene. However, they should be ignored for determining the material properties of object surfaces.

The first computational step in each of the three systems consists in detecting the respective features. Following feature detection, representations of surfaces [48], gradients [49–51], and texture [11], respectively, are eventually build by each corresponding system. Our normal visual perception would then be the result of superimposing all three representations (brightness perception). Having three separate representations (instead of merely a single one) has the advantage that higher-level cortical information processing circuits could selectively suppress or reactivate texture and/or gradient representations in addition to surface representations. This flexibility allows for the different requirements for deriving the material properties of objects. For instance, surface representations are directly linked to the perception of reflectance (“lightness”) and object recognition, respectively. In contrast, the computation of surface curvature and the interpretation of the three-dimensional scene structure relies on gradients (e.g., shape from shading) and/or texture representations (texturecompression with distance).

How do we identify texture features? We start with processing a grayscale image with a retinal model which is based on a modification of Eq. (10.6):

10.13

is just the input image itself – so the center kernel (also known as the receptive field) is just one pixel. is the result of convolving the input image with a surround kernel that has at north, east, west, and south positions. Elsewhere it is zero. Thus, approximates the (negative) second spatial derivative of the image. Accordingly, we can define two types of ganglion cell responses: ON-cells are defined by and respond preferably to (spatial) increments in luminance. OFF-cells have and prefer decrements in luminance. Figure 10.5(b) shows the output of Eq. (10.13), which is the half-wave rectified membrane potential . Biological ganglion cell responses saturate with increasing contrast. This is modeled here by , where corresponds to self-inhibition – the more center and surround are activated, the stronger. Mathematically, , with a constant that determines how fast the responses saturate. Why did we not simply set (and ), and (and ) in Eq. (10.6) (vice versa for an OFF-cell)? This is because in the latter case the ON- and OFF-response amplitudes would be different for a luminance step (cf. Eq. (10.7)). Luminance steps are odd-symmetric features and are not texture. Thus, we want to suppress them, and suppression is easier if ON- and OFF-response amplitudes (to odd-symmetric features) are equal.

Figure 10.5 Texture segregation. Illustration of processing a grayscale image with the texture system. (a) Input image “Lena” with pixels and superimposed numbers. (b) The output of the retina (Eq. (10.13)). ON-activity is white, while OFF is black. (c) The analysis of the retinal image proceeds along four orientation channels. The image shows an intermediate result after summing across the four orientations (texture brightness in white, texture darkness in black). After this, a local WTA-competition suppresses residual features that are not desired, leading to the texture representation. (d) This is the texture representation of the input image and represents the final output of the texture system. As before, texture brightness is white and texture darkness is black.

In response to even-symmetric features (i.e., texture features) we can distinguish two (quasi one-dimensional) response patterns. A black line on a white background produces an ON–OFF–ON (i.e., LDL) response: a central OFF-response, and two flanking ON-responses with much smaller amplitudes. Analogously, a bright line on a dark background will trigger an OFF–ON–OFF or DLD response pattern. ON- and OFF-responses to lines (and edges) vary essentially in one dimension. Accordingly, we analyze them along four orientations. Orientation-selective responses (without blurring) are established by convolving the OFF-channel with an oriented Gaussian kernel, and subtract it from the (not blurred) ON-channel. This defines texture brightness. The channel for texture darkness is defined by subtracting blurred ON-responses from OFF-responses. Subsequently, even-symmetric response patterns are further enhanced with respect to surface features. In order to boost a DLD pattern, the left-OFF is multiplied with its central-ON and its right-OFF(analogous for LDL patterns). Note that surface response pattern (LD or DL, respectively) ideally has only one flanking response. Dendritic trees are a plausible neurophysiological candidate for implementing such a “logic” AND gate (simultaneous left and central and right response) [6].

In the subsequent stage the orientated texture responses are summed across orientations, leaving nonoriented responses (Figure 10.5(c)). By means of a winner-takes-all (WTA) competition between adjacent (nonoriented) texture brightness (“L”) and texture darkness (“D”), it is now possible to suppress the residual surface features on the one hand, and the flanking responses from the texture features, on the other. For example, an LDL response pattern will generate a competition between L and D (on the left side) and D and L (right side). Since for a texture feature the central response is bigger, it will survive the competition with the flanking responses. The flanking responses, however, will not. A surface response (say DL) will not survive either, because D- and L-responses have equal amplitudes. The local spatial WTA-competition is established with a nonlinear diffusion paradigm [52]. The final output of the texture system (i.e., a texture representation) is computed according to Eq. (10.6), where texture brightness acts excitatory, and texture darkness inhibitory. An illustration of a texture representation is shown in Figure 10.5(d).

10.5 Application 3: Detection of Collision Threats

Many animals show avoidance reactions in response to rapidly approaching objects or other animals [53, 54]. Visual collision detection also has attracted attention from engineering because of its prospective applications, for example, in robotics or in driver assistant systems. It is widely accepted that visual collision detection in biology is mainly based on two angular variables: (i) The angular size of an approaching object, and (ii) its angular velocity or rate of expansion (the dot denotes derivative in time). If an object approaches an observer with constant velocity, then both angular variables show a nearly exponential increase with time. Biological collision avoidance does not stop here, but computes mathematical functions (here referred to as optical variables) of and . Accordingly, three principal classes of collision-sensitive neurons have been identified [55]. These classes of neurons can be found in animals as different as insects or birds. Therefore, evolution came up with similar computational principles that are shared across many species [36].

A particularly well-studied neuron is the LGMD neuron of the locust visual system, because the neuron is relatively big and easy to access. Responses of the LGMD to object approaches can be described by the so-called eta-function: [56]. There is some evidence that the LGMD biophysically implements [57] (but see Ref. [58, 59]): logarithmic encoding converts the product into a sum, with representing excitation and inhibition. One distinctive property of the eta-function is a response maximum before collision would occur. The time of the response maximum is determined by the constant and always occurs at the fixed angular size .

So much for the theory – but how can the angular variables be computed from a sequence of image frames? The model which is presented below (first proposed in Ref. [12]) does not compute them explicitly, although its output resembles the eta-function. However, the eta-function is not explicitly computed either. Without going too far into an ongoing debate on the biophysical details of the computations which are carried out by the LGMD [53, 58, 60], the model rests on lateral inhibition in order to suppress self-motion and background movement [61].

The first stage of the model computes the difference between two consecutive image frames and (assuming grayscale videos):

10.14

where – we omit spatial indices and time for convenience. The last equation and all subsequent ones derives directly from equation (10.6). Further processing in the model proceeds along two parallel pathways. The ON-pathway is defined by the positive values of , that is . The OFF-pathway is defined by . In the absence of background movement, is related to angular velocity: if an approaching object is yet far away, then the sum will increase very slowly. In the last phase of an approach (shortly before collision), however, the sum increases steeply.

The second stage has two diffusion layers (one for ON, another one for OFF) that implement lateral inhibition:

10.15

where is the diffusion coefficient (cf. Eq. (10.12)). The diffusion layers act inhibitory (see below) and serve to attenuate background movement and translatory motion as caused by self-movement. If an approaching object is sufficiently far away, then the spatial variations (as a function of time) in are small. Similarly, translatory motion at low speed will also generate small spatial displacements. Activity propagation proceeds at constant speed and thus acts as a predictor for small movement patterns. But diffusion cannot keep up with those spatial variations as they are generated in the late phase of an approach. The output of the diffusion layer is and , respectively (the tilde denotes half-wave rectified variables).

The inputs into the diffusion layers and , respectively, are brought about by feeding back activity from the third stage of the model:

10.16

with excitatory input and inhibitory input ( and analogously). Hence, receives two types of inhibition from . First, directly inhibits via the inhibitory input . Second, gates the excitatory input : activity from the first stage is attenuated at those positions where . This means that can only decrease where and feedback from to assures also that the activity in will not grow further then. In this way, the situation that the diffusion layers continuously accumulate activity and eventually “drown” (i.e., at all positions ) is largely avoided.Drowning otherwise would occur in the presence of strong background motion, making the model essentially blind to object approaches. The use of two diffusion layers contributes to a further reduction of drowning.

The fifth and final stage of the model represents the LGMD neuron and spatially sums the output from the previous stage:

10.17

where and and analogously for . is a synaptic weight. Notice that, whereas and are two-dimensional variables in space, is a scalar. The final model output corresponds to the two half-wave rectified LGMD activities and , respectively. Figure 10.6 shows representative frames from two video sequences that were used as input to the model. Figure 10.7 shows the corresponding output as computed by the last equation. Simulated LGMD responses are nice and clean in the absence of background movement (Figure 10.7(a)). The presence of background movement, on the other hand, produces spurious LGMD activation before collision occurs (Figure 10.7(b)).

Figure 10.6 Video sequences showing object approaches. Two video sequences which served as input to Eq. (10.14). (a) Representative frames of a video where a car drives to a still observer. Except for some camera shake, there is no background motion present in this video. The car does actually not collide with the observer. (b) The video frames show a car (representing the observer) driving against a static obstacle. This sequence implies background motion. Here the observer actually collides with the balloon car, which flies through the air after the impact.

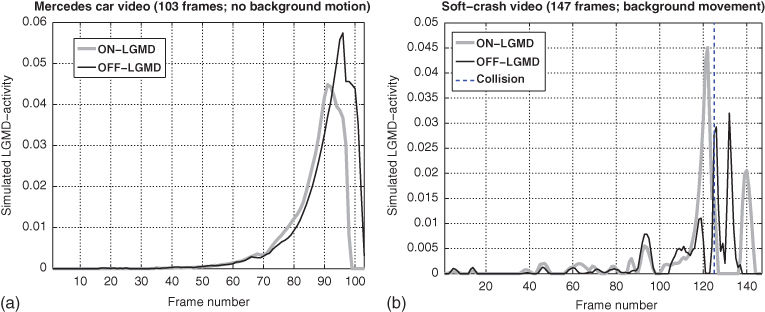
Figure 10.7 Simulated LDMD responses. Both figures show the rectified LGMD activities (gray curves; label “ON-LGMD”) and (black curves; label “OFF-LGMD”) as computed by Eq. (10.17). LGMD activities are one-dimensional signals that vary with time (the abscissa shows the frame number instead of time). (a) Responses to the video shown in Figure 10.6 (a). The observer does not move and no background motion is generated. Both LDMD responses peak before collision would occur. (b) Responses to the video shown in Figure 10.6 (b). Here the observer moves, and the resulting background motion causes spurious LGMD activity with small amplitude before collision. The collision time is indicated by the dashed vertical line. ON-LGMD activity peaks a few frames before collision. OFF-LGMD activity after collision is generated by the balloon car swirling through the air while it is moving away from the observer.

10.6 Conclusions

Neurodynamical models (which are suitable for processing real-world images) and PDE (partial differential equation)-based image processing algorithms typically differ in the way they are designed, and in their respective predictions with regard to neuroscience. PDE-based image processing algorithms derive often from an optimization principle (such as minimizing an energy functional). As a result, a set of differential equations is usually obtained, which evolves over time [62]. Many of these algorithms are designed ad hoc for specific image processing tasks (e.g., optical flow computation [63], segmentation [64], or denoising [65]), but they are usually not designed according to neuronal circuits. Similarly, they usually do not predict psychophysical results. Some remarkable exceptions, however, do exist. For example, the color enhancement algorithm described in reference [66] is based on a perceptually motivated energy functional, which includes a contrast term (enforcing local contrast enhancement) and a dispersion term (implementing the gray-world assumption and enforcing fidelity to the data). In a similar vein, the Retinex algorithm – for estimating perceived reflectance (lightness) – could also be casted into a variational framework [67]. An algorithm for tone mapping of high dynamic range images was originally motivated by compressing high contrasts while preserving low contrasts [68]. Although the authors did not explicitly acknowledge any inspiration from neuroscience, it is nevertheless striking how the algorithm resembles filling-in architectures [48]. Filling-in has been proposed as a mechanism for computing smooth representations of object surfaces in the visual system. Smooth representations imply that surfaces are “tagged” with perceptual values such as color, movement direction, depth, or lightness [69]. Filling-in is often modeled by (lateral) activity propagation within compartments, which are defined through contrast boundaries [70]. A recently proposed filling-in-based computer vision algorithm identifies regions with a coherent movement direction from a (initially noisy) optic flow field [71]. The algorithm proposes also a solution to the so-called aperture problem, and is based on corresponding computations of the brain's visual system [72]. A further method that resembles the filling-in process is image inpainting (e.g., Ref. [73]). Image inpainting completes missing regions by propagating the structure of the surround into that region. Although image inpainting has not been related to neurophysiological principles, similar (slow) filling-in effects seem to exist also in the brain (e.g., texture filling-in Ref. [74]).

Acknowledgments

MSK acknowledges support from a Ramon & Cajal grant from the Spanish government, the “Retención de talento” program from the University of Barcelona, and the national grants DPI2010-21513 and PSI2013-41568-P.

References

1. 1. Rumelhart, D.E., Hinton, G.E., and Williams, R.J. (1986) Learning representations by back-propagating errors. Nature, 323, 533–536.

2. 2. Hinton, G.E. and Salakhutdinov, R.R. (2006) Reducing the dimensionality of data with neural networks. Science, 313, 504–507.

3. 3. Mel, B. (1994) Information processing in dendritic trees. Neural Comput., 6, 1031–1085.

4. 4. Häusser, M., Spruston, N., and Stuart, G. (2000) Diversity and dynamics of dendritic signalling. Science, 290, 739–744.

5. 5. Segev, I. and London, M. (2000) Untangling dendrites with quantitative models. Science, 290, 744–750.

6. 6. London, M. and Häusser, M. (2005) Dendritic computation. Annu. Rev. Neurosci., 28, 503–532.

7. 7. Brette, R. et al. (2007) Simulation of networks of spiking neurons: a review of tools and strategies. J. Comput. Neurosci., 23, 349–398.

8. 8. Hodkin, A. and Huxley, A. (1952) A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol., 117, 500–544.

9. 9. Izhikevich, E. (2004) Which model to use for cortical spiking neurons? IEEE Trans. Neural Netw., 15, 1063–1070.

10.10. Izhikevich, E. (2003) Simple model of spiking neurons. IEEE Trans. Neural Netw., 14, 1569–1572.

11.11. Keil, M. (2003) Neural architectures for unifying brightness perception and image processing. PhD thesis. Universität Ulm, Faculty for Computer Science, Ulm, Germany, http://vts.uni-ulm.de/doc.asp?id=3042 (accessed 5 May 2015).

12.12. Keil, M., Roca-Morena, E., and Rodríguez-Vázquez, A. (2004) A neural model of the locust visual system for detection of object approaches with real-world scenes. Proceedings of the 4th IASTED International Conference, vol. 5119, Marbella, Spain, pp. 340–345.

13.13. Kolb, H. (1977) The organization of the outer plexiform layer in the retina of the cat: electron microscopic observations. J. Neurocytol., 6, 131–153.

14.14. Nelson, R. et al. (1985) Spectral mechanisms in cat horizontal cells, in Neurocircuitry of the Retina: A Cajal Memorial (ed. A. Gallego), Elsevier, New York, pp. 109–121.

15.15. Galarreta, M. and Hestrin, S. (1999) A network of fast-spiking cells in the neocortex connected by electrical synapses. Nature, 402, 72–75.

16.16. Gibson, J., Beierlein, M., and Connors, B. (1999) Two networks of electrically coupled inhibitory neurons in neocortex. Nature, 402, 75–79.

17.17. O'Shea, M. and Rowell, C. (1975) A spike-transmitting electrical synapse between visual interneurons in the locust movement detector system. J. Comp. Physiol., 97, 875–885.

18.18. Rind, F. (1984) A chemical synapse between two motion detecting neurons in the locust brain. J. Exp. Biol., 110, 143–167.

19.19. Killmann, F. and Schürmann, F. (1985) Both electrical and chemical transmission between the lobula giant movement detector and the descending contralateral movement detector neurons of locusts are supported by electron microscopy. J. Neurocytol., 14, 637–652.

20.20. Killmann, F., Gras, H., and Schürmann, F. (1999) Types, numbers and distribution of synapses on the dendritic tree of an identified visual interneuron in the brain of the locust. Cell Tissue Res., 296, 645–665.

21.21. Markram, H., Lubke, M., Frotscher, J., and Sakmann, B. (1997) Regulation of synaptic efficacy by coincidence of postsynaptic APs and EPSPs. Science, 275, 213–215.

22.22. Wang, H.-X. et al. (2005) Coactivation and timing-dependent integration of synaptic potentiation and depression. Nat. Neurosci., 8, 187–193.

23.23. Hebb, D. (1949) The Organization of Behavior, John Wiley & Sons, Inc., New York.

24.24. Song, S., Miller, K., and Abbott, L. (2000) Competitive Hebbian learning through spike-timing-dependent synaptic plasticity. Nat. Neurosci., 3, 919–926.

25.25. Magee, J. and Johnston, D.A. (1997) Synaptically controlled, associative signal for Hebbian plasticity in hippocampal neurons. Science, 275, 209–213.

26.26. Strang, G. (2007) Computational Science and Engineering, Wellesley-Cambride Press, Wellesley, MA.

27.27. Press, W. et al. (2007) Numerical Recipes - The Art of Scientific Computing, 3rd edn, Cambridge University Press, New York.

28.28. Mel, B. (1993) Synaptic integration in an excitable dendritic tree. J. Neurophysiol., 70, 1086–1101.

29.29. Jonas, P. and Buzsaki, G. (2007) Neural inhibition. Scholarpedia, 2, 3286.

30.30. van Vreeswijk, C. and Sompolinsky, H. (1996) Chaos in neuronal networks with balanced excitatory and inhibitory activity. Science, 274, 1724–1726.

31.31. Haider, B. et al. (2006) Neocortical network activity in vivo is generated through a dynamic balance of excitation and inhibition. J. Neurosci., 26, 4535–4545.

32.32. Holt, G. and Koch, C. (1997) Shunting inhibition does not have a divisive effect on firing rates. Neural Comput., 9, 1001–1013.

33.33. Abbott, L. and Chance, F. (2005) Drivers and modulators from push-pull balanced synaptic input. Curr. Biol., 147–155, doi: 10.1016/S0079-6123(05)49011-1.

34.34. Huxter, J., Burgess, N., and O'Keefe, J. (2003) Independent rate and temporal coding in hippocampal pyramidal cells. Nature, 425, 828–831.

35.35. Alle, H. and Geiger, J. (2006) Combined analog and action potential coding in hippocampal mossy fibers. Science, 311, 1290–1293.

36.36. Keil, M. and López-Moliner, J. (2012) Unifying time to contact estimation and collision avoidance across species. PLoS Comput. Biol., 8, e1002625, doi: 10.1371/journal.pcbi.1002625.

37.37. Pitkov, X. and Meister, M. (2012) Decorrelation and efficient coding by retinal ganglion cells. Nat. Neurosci., 15, 497–643.

38.38. Hosoya, T., Baccus, S., and Meister, M. (2005) Dynamic predictive coding by the retina. Nature, 436, 71–77.

39.39. Doi, E. et al. (2012) Efficient coding of spatial information in the primate retina. J. Neurosci., 32, 16256–16264.

40.40. Attneave, F. (1954) Some informational aspects of visual perception. Psychol. Rev., 61, 183–193.

41.41. Niven, J., Anderson, J., and Laughlin, S. (2007) Fly photoreceptors demonstrate energy-information trade-offs in neural coding. PLoS Biol., 5, e116.

42.42. Balasubramanian, V. and Berry, M. (2002) A test of metabolically efficient coding in the retina. Netw. Comput. Neural Syst., 13, 531–552.

43.43. Rodieck, R.W. (1965) Quantitative analysis of cat retinal ganglion cell response to visual stimuli. Vision Res., 5, 583–601.

44.44. Kuffler, S. (1953) Discharge patterns and functional organization of mammalian retina. J. Neurophysiol., 16, 37–68.

45.45. Chichilnisky, E. and Kalmar, R. (2002) Functional asymmetries in ON and OFF ganglion cells of primate retina. J. Neurosci., 22, 2737–2747.

46.46. Kaplan, E. and Benardete, E. (2001) The dynamics of primate retinal ganglion cell. Prog. Brain Res., 134, 17–34.

47.47. Pandarinath, J., an Victor, C., and Nirenberg, S. (2010) Symmetry breakdown in the ON and OFF pathways of the retina at night: functional implications. J. Neurosci., 30, 10006–10014.

48.48. Keil, M. et al. (2005) Recovering real-world images from single-scale boundaries with a novel filling-in architecture. Neural Netw., 18, 1319–1331.

49.49. Keil, M., Cristóbal, G., and Neumann, H. (2006) Gradient representation and perception in the early visual system - a novel account to Mach band formation. Vision Res., 46, 2659–2674.

50.50. Keil, M. (2006) Smooth gradient representations as a unifying account of Chevreul's illusion, Mach bands, and a variant of the Ehrenstein disk. Neural Comput., 18, 871–903.

51.51. Keil, M. (2007) Gradient representations and the perception of luminosity. Vision Res., 47, 3360–3372.

52.52. Keil, M. (2008) Local to global normalization dynamic by nonlinear local interactions. Physica D, 237, 732–744.

53.53. Rind, F. and Simmons, P. (1999) Seeing what is coming: building collision-sensitive neurons. Trends Neurosci., 22, 215–220.

54.54. Rind, F. and Santer, D. (2004) Collision avoidance and a looming sensitive neuron: size matters but biggest is not necessarily best. Proc. R. Soc. London, Ser. B, 271, S27–S29, doi: 10.1098/rsbl.2003.0096.

55.55. Sun, H. and Frost, B. (1998) Computation of different optical variables of looming objects in pigeon nucleus rotundus neurons. Nat. Neurosci., 1, 296–303.

56.56. Hatsopoulos, N., Gabbiani, F., and Laurent, G. (1995) Elementary computation of object approach by a wide-field visual neuron. Science, 270, 1000–1003.

57.57. Gabbiani, F. et al. (2002) Multiplicative computation in a visual neuron sensitive to looming. Nature, 420, 320–324.

58.58. Keil, M. (2011) Emergence of multiplication in a biophysical model of a wide-field visual neuron for computing object approaches: dynamics, peaks, & fits, Advances in Neural Information Processing Systems, vol. 24 (eds J. Shawe-Taylor, R. Zemel, P. Bartlett, F. Pereira, and K. Weinberger), pp. 469–477, http://arxiv.org/abs/1110.0433.

59.59. Keil, M. (2012) The role of neural noise in perceiving looming objects and eluding predators. Perception, S41, 162.

60.60. Gabbiani, F. et al. (1999) The many ways of building collision-sensitive neurons. Trends Neurosci., 22, 437–438.

61.61. Rind, F. and Bramwell, D. (1996) Neural network based on the input organization of an identified neuron signaling implending collision. J. Neurophysiol., 75, 967–985.

62.62. Chan, T., Shen, J., and Vese, L. (2003) Variational PDE models in image processing. Not. Am. Math. Soc., 50 (1), 14–26.

63.63. Aubert, G., Deriche, R., and Kornprobst, P. (1999) Computing optical flow via variational techniques. SIAM J. Appl. Math., 60, 156–182.

64.64. Vitti, A. (2012) The Mumford–Shah variational model for image segmentation: an overview of the theory, implementation and use. ISPRS J. Photogramm. Remote Sens., 69, 50–64.

65.65. Rudin, L., Osher, S., and Fatemi, E. (1992) Nonlinear total variation based noise removal algorithm. Physica D, 60, 259–268.

66.66. Palma-Amestoy, R. et al. (2009) A perceptually inspired variational framework for color enhancement. IEEE Trans. Pattern Anal. Mach. Intell., 31, 458–474.

67.67. Kimmel, R. et al. (2003) A variational framework for retinex. Int. J. Comput. Vision, 52, 7–23.

68.68. Fattal, R., Lischinski, D., and Werman, M. (2002) Gradient domain high dynamic range compression, in SIGGRAPH '02: ACM SIGGRAPH 2002 Conference Abstracts and Applications, ACM, New York.

69.69. Komatsu, H. (2006) The neural mechanisms of perceptual filling-in. Nat. Rev. Neurosci., 7, 220–231.

70.70. Grossberg, S. and Mingolla, E. (1987) Neural dynamics of surface perception: boundary webs, illuminants, and shape-from-shading. Computer Vision Graph. Image Process., 37, 116–165.

71.71. Bayerl, P. and Neumann, H. (2007) A fast biologically inspired algorithm for recurrent motion estimation. IEEE Trans. Pattern Anal. Mach. Intell., 3, 904–910.

72.72. Bayerl, P. and Neumann, H. (2004) Disambiguating visual motion through contextual feedback modulation. Neural Comput., 16, 2041–2066.

73.73. Bugeau, A. et al. (2010) A comprehensive framework for image inpainting. IEEE Trans. Image Process., 19, 2634–2645.

74.74. Motoyoshi, I. (1999) Texture filling-in and texture segregation revealed by transient masking. Vision Res., 39, 1285–1291.

¹ In the peripheral nervous system of vertebrates, excitatory synapses are activated instead by acetylcholine (ACh)² -Methyl-D-aspartat³ -Amino-3-hydroxy-5-methyl-4-isoxazole propionic acid⁴ From Ref. [29]: -aminobutyric acid⁵ GABA, are ligand-gated ion channels permeable to . Postsynaptic GABA are heptahelical receptors coupled to inwardly rectifying channels. Finally, GABA are ligand-gated channels, which are primarily expressed in the retina.⁶ In this case, the response threshold . For arbitrary thresholds, the right hand side would become .