Foundations of Algorithms (2015)

Chapter 11 Number-Theoretic Algorithms

Suppose Bob wants to send Alice a secret love note over the Internet, but he is afraid some of his friends might intercept the message and read it. If he could encode the message so that it appears as gibberish and only Alice could decode the gibberish back to the original message, he would not need to fear his friends intercepting the message. Number-theoretic algorithms can help Bob develop a system for doing this. We discuss such algorithms next.

Number theory is the branch of mathematics concerned with the properties of the integers. Number-theoretic algorithms are algorithms that solve problems involving the integers. For example, a number-theoretic algorithm might find the greatest common divisor of two integers. After reviewing basic number theory in Section 11.1, we present Euclid’s algorithm for finding the greatest common divisor in Section 11.2. Next, Section 11.3 reviews modular arithmetic, Section 11.4 shows an algorithm for solving modular linear equations, and Section 11.5 develops an algorithm for computing modular powers. Section 11.6 concerns algorithms for determining whether a number is prime. An important application of number-theoretic algorithms is in cryptography, which is the discipline concerned with encrypting a message sent from one party to another, so that someone who intercepts the message will not be able to decode it. In Section 11.7 we present the Rivest-Shamir-Adelman (RSA) public-key cryptosystem, which is a system that does this.

Before proceeding, we note that in this chapter we revert back to developing algorithms as we did in Chapters 2 through 6. However, unlike the methods presented in those chapters, number-theoretic algorithms are concerned with solving a certain type of problem (namely ones involving the integers); they are not algorithms that share a common technique.

11.1 Number Theory Review

We review some basic elements of number theory.

• 11.1.1 Composite and Prime Numbers

The set

is called the set of integers. For any two integers n, h ∈ Z, we say h divides n, denoted h|n, if there is some integer k such that n = kh. If h|n, we also say n is divisible by h, n is a multiple of h, and h is a divisor or factor of n.

Example 11.1

We have that 4|20 since 20 = (5) (4). The integer 3 does not divide 20 since there is no integer k such that 20 = (k) (3).

Example 11.2

The divisors of 12 are

An integer n > 1 whose only positive divisors are 1 and n is called a prime number or simply a prime. A prime number has no factors. An integer n > 1 that is not prime is called a composite number. A composite number has at least one factor.

Example 11.3

The first 10 primes are

Example 11.4

The integer 12 is composite because it has the divisors 2, 3, 4, and 6. The integer 4 is composite because it has the divisor 2.

• 11.1.2 Greatest Common Divisor

If h|n and h|m, then h is called a common divisor of n and m. If n and m are not both zero, the greatest common divisor of n and m, denoted gcd(n, m), is the largest integer that divides both of them.

Example 11.5

The positive divisors of 24 are

and the positive divisors of 30 are

So the common positive divisors of 24 and 30 are

and the value of gcd(24, 30) is 6.

We have the following theorems concerning common divisors:

Theorem 11.1

If h|n and h|m, then for any integers i and j

Proof: Since h|n and h|m, there exist integers k and l such that n = kh and m = lh. Therefore,

which means h| (in + jm).

Before proceeding, we need more definitions. For any two integers n and m, where m ≠ 0, the quotient q of n divided by m is given by

and the remainder r of dividing n by m is given by

The remainder is denoted n mod m. It is not hard to see that if m > 0 then 0 ≤ r < m, and if m < 0 then m < r ≤ 0. So we have

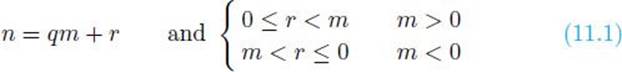
The division algorithm says not only that the integers q and r in Equality 11.1 exist but also that they are unique.

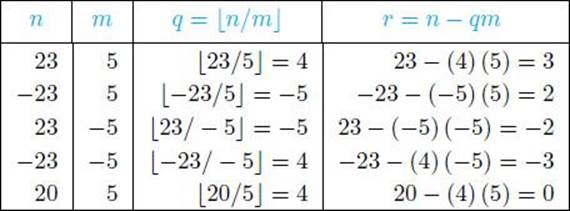
Example 11.6

The following table shows some quotients and remainders:

Theorem 11.2

Let n and m be integers, not both 0, and let

That is, d is the smallest positive linear combination of n and m. Then

Proof: Let i and j be the integers that yield the minimal value d. That is, d = in + jm. Furthermore, let q and r be the quotient and remainder respectively, of dividing n by d. Then owing to Equality 11.1 and the fact that d is positive,

We therefore have

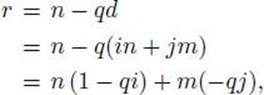
which means that r is a linear combination of n and m. Since d is the smallest positive linear combination of n and m and r < d, we conclude r = 0, which means d|n. Similarly, d|m. Therefore, d is a common divisor of m and n, which means

Since the gcd(n, m) divides both n and m, and d = in + jm, Theorem 11.1 implies gcd(n, m)|d. We conclude

Combining these last two inequalities, we have d = gcd(n, m).

Example 11.7

We have that gcd(12, 8) = 4, and

Corollary 11.1

Suppose n and m are integers, not both 0. Then every common divisor of n and m is a divisor of gcd(n, m). That is, if h|n and h|m, then

Proof: By the preceding theorem, gcd(n, m) is a linear combination of n and m. The proof now follows from Theorem 11.1.

Example 11.8

As shown in Example 11.5, the common positive divisors of 24 and 30 are

and the value of gcd(24, 30) is 6. As the previous corollary implies, 1, 2, 3, and 6 all divide 6.

Theorem 11.3

Suppose we have integers n ≥ 0 and m > 0. If we let r = nmodm, then

If n = 0, r = m and the equality obviously holds. Otherwise, we will show that gcd(n, m) and gcd(m, r) each divide each other. It is left as an exercise to show that two positive integers divide each other if and only if they are equal, which will complete the proof of the theorem. First we show gcd(n, m)| gcd(m, r). If we let d′ = gcd(n, m), then d′|n and d′|m. Furthermore,

where q is the quotient of n divided by m, which means n is a linear combination of m and r. Theorem 11.1 therefore implies d″|n. Since d″|m and d″|n, Corollary 11.1 implies

which completes the proof of this direction. Next show gcd(m, r)| gcd(n, m). If we let d″ = gcd(m, r), then d″|m and d″|r. Furthermore,

where q is the quotient of n divided by m, which means n is a linear combination of m and r. Theorem 11.1 therefore implies d″|n. Since d″|m and d″|n, Corollary 11.1 implies

which completes the proof of this direction.

Example 11.9

According to the previous theorem,

because 16 = 64 mod 24. We can continue in this manner to determine gcd(64, 24). That is,

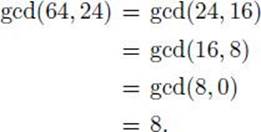
• 11.1.3 Prime Factorization

Every integer greater than one can be written as a unique product of primes. We next develop theory that proves this assertion.

Two integers n and h, not both zero, are called relatively prime if gcd(n, h) = 1.

Example 11.10

The integers 12 and 25 are relatively prime because gcd(12, 25) = 1. The integers 12 and 15 are not relatively prime because gcd(12, 15) = 3.

Theorem 11.4

If h and m are relatively prime, and h divides nm, then h divides n. That is, gcd(h, m) = 1 and h|nm implies h|n.

Proof: Theorem 11.2 implies there are integers i and j such that

Multiplying this equality by n yields

Clearly, h divides the first term on the left-hand side of this equality, and, since h|nm, h also divides the second term. Therefore, h divides the left-hand side, which means h divides n.

Example 11.11

The integers 9 and 4 are relatively prime, 9|72, and 72 = 18 × 4. As the previous theorem implies, 9|18.

Corollary 11.2

Given integers n, m, and prime integer p, if p|nm, then p|n or p|m (inclusive).

Proof: The proof follows easily from Theorem 11.4.

The theorem that follows is called the unique factorization theorem and the fundamental theorem of arithmetic.

Theorem 11.5

Every integer n > 1 has a unique factorization as a product of prime numbers. That is,

where p₁ < p₂ < · · · < p_j are primes, and this representation of n is unique. The integer k_i is called the order of p_i in n.

Proof: We use induction to prove such a representation exists.

Induction base: We have 2 = 2¹.

Induction hypothesis: Suppose all integers m such that 2 ≤ m < n can be written as a product of prime numbers.

Induction step: If n is prime, then n = n¹ is our representation. Otherwise, n is composite, which means there exists integers m, h > 1 such that

Clearly m, h < n. Therefore, by the induction hypothesis, m and h can each be written as a product of primes. That is,

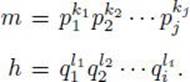
Since n = mh,

We obtain our desired representation by grouping primes that are equal and arranging the terms according to increasing values of the primes. This completes the induction proof.

The fact that the product is unique follows from Corollary 11.2 and is left as an exercise.

Example 11.12

We have that

The previous theorem says the representation on the right-hand side of this equality is unique.

Theorem 11.6

The gcd(n, m) is a product of the primes that are common to n and m, where the power of each prime in the product is the smaller of its orders in n and m.

Proof: The proof is left as an exercise.

Example 11.13

We have 300 = 2² × 3¹ × 5² and 1,125 = 3² × 5³. So gcd(300, 1,125) = 2⁰ × 3¹ × 5² = 75.

• 11.1.4 Least Common Multiple

A concept similar to that of the greatest common divisor is that of the least common multiple. If n and m are both nonzero, the least common multiple of n and m, denoted lcm(n, m), is the smallest positive integer that they both divide.

Example 11.14

The lcm(6, 9) = 18 because 6|18, 9|18, and there is no smaller positive integer that they both divide.

Theorem 11.7

The lcm(n, m) is a product of the primes that are common to n and m, where the power of each prime in the product is the larger of its orders in n and m.

Proof: The proof is left as an exercise.

Example 11.15

We have 12 = 2² ×3¹ and 45 = 3² ×5¹. So lcm(12, 45) = 2² ×3² ×5¹ = 180.

11.2 Computing the Greatest Common Divisor

Theorem 11.6 gives us a straightforward way to compute the greatest common divisor of two such integers. We simply find the unique factorizations for the two integers, determine which primes they have in common, and determine the greatest common divisor to be a product whose terms are these common primes, where the power of each prime in the product is the smaller of its orders in the two integers. Example 11.13 illustrated this. Another example follows:

Example 11.16

We have

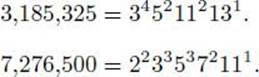
So

The problem with the previous technique is that it is not easy to find the unique factorization of an integer. You would have had some difficulty factoring the integers in the previous example if we had not given you the factorization. Now imagine the difficulty if the integers had 25 digits instead of 7. Indeed, no one has ever found a polynomial-time algorithm for determining the factorization of an integer. Next we show a more efficient way to compute the greatest common divisor.

• 11.2.1 Euclid’s Algorithm

Theorem 11.1 gives us a straightforward method for determining the greatest common divisor of two integers. Example 11.9 illustrates the method. Namely, to find the gcd(n, m) we recursively apply the equality in the theorem until m = 0, and then we return n. This method is called Euclid’s algorithm because it was developed by Euclid around 300 B.C. The algorithm follows:

Algorithm 11.1

Euclid’s Algorithm

Problem: Compute the greatest common divisor of a positive integer and a nonnegative integer.

Inputs: a positive integer n and a nonnegative integer m.

Outputs: the greatest common divisor of n and m.

Example 11.17

We find the greatest common divisor of the numbers in Example 11.16 using Algorithm 11.1.

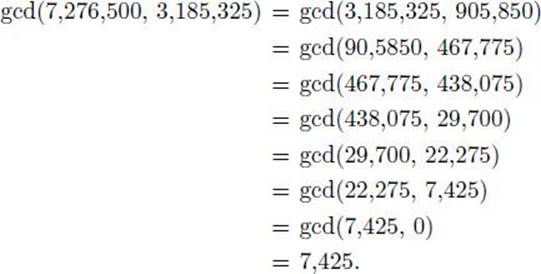
It seemed pretty easy for us to compute the greatest common divisor using Euclid’s algorithm. Let’s analyze Algorithm 11.1 to see just how easy it is. First we need a lemma and a theorem.

Lemma 11.1

If n > m ≥ 1 and the call gcd(n, m) (in Algorithm 11.1) results in k recursive calls where k ≥ 1, then

where f_k is the kth number in the Fibonacci sequence.

Proof: The proof is by induction.

Induction base: Suppose the call gcd(n, m) results in 1 recursive call. Since m ≥ 1

Since n > m, we have n ≥ 2, which means

Induction hypothesis: Assume the lemma is true if k − 1 recursive calls are made.

Induction step: Show the lemma is true if k ≥ 2 recursive calls are made. We need to show

The first recursive call is gcd(m, n mod m). Since there are k recursive calls in all, this call must require k − 1 recursive calls. Since k ≥ 2, there is at least one more recursive call, which means n mod m ≥ 1. Therefore, since m > n mod m, the conditions of the induction hypothesis are satisfied, which means

So we’ve arrived at one of the inequalities we needed to show. Towards showing the other, we have

where q is the quotient of dividing n by m. Since n > m, q ≥ 1. Inequality 11.2 and Equality 11.3 therefore imply

This completes the proof.

Theorem 11.8

(Lamé) For every integer k ≥ 1 if n > m ≥ 1 and m ≤ f_k, the kth number in the Fibonacci sequence, then the call gcd(n, m) (in Algorithm 11.1) results in less than k recursive calls.

Proof: The proof follows immediately from the previous lemma.

Next we analyze Algorithm 11.1. Recall from Section 9.2 that in numeric algorithms, the number(s) that is the input is not the input size. Rather, the input size is the number of characters it takes to write the input. If we use binary encoding, the input size is the number of bits it takes to encode the number(s), which is about equal to the lg of the number(s).

Analysis of Algorithm 11.1

Worst-Case Time Complexity (Euclid’s Algorithm)

Basic operation: one bit manipulation in the computation of a remainder.

Input size: the number of bits s it takes to encode n and the number of bits t it takes to encode m. That is,

Without loss of generality, we will analyze the case where 1 ≤ m < n. That is, if m = n, there will be no recursive calls, while if m > n, the first recursive call will be gcd(m, n), which means the first argument is larger.

We will not determine the exact time complexity. Rather we will first show the number of recursive calls Calls(s, t) is Θ(t), and then we will find a bound for the worst-case time complexity.

First we show Calls(s, t) is in O(t). Assuming m ≥ 2, let f_k be the number in the Fibonacci sequence such that

In Example B.9 in Section B.2.1 we show that

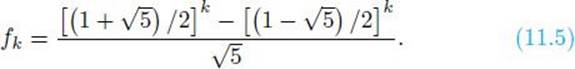
Either k − 1 is odd or k − 2 is odd. Without loss of generality, assume k − 1 is odd. Owing to Equality 11.5 and Inequality 11.4, we have

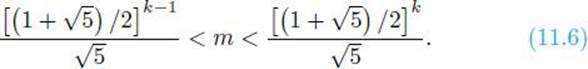
Owing to Equality 11.4, Theorem 11.8 implies

Inequalities 11.6 and 11.7 imply that

It is left as an exercise to show that the call gcd(f_k+1, f_k) requires exactly k − 1 recursive calls. We conclude that

where W calls(s, t) is the worst-case number of recursive calls for input size s, t.

For each recursive call, we compute one remainder. It is left as an exercise to show that, if we use the standard long division algorithm (as discussed in Section 2.6) to compute the remainder, the worst case number of bit manipulations needed to compute r = n mod m for m < n is bounded above by

where q is the quotient of dividing n by m, and c is a constant. We will show if r > 0, then, for the input size sufficiently larger, the worst case number of bit manipulations needed to compute r is bounded above by

To that end, since q = (n − r)/m and 1 ≤ r < m,

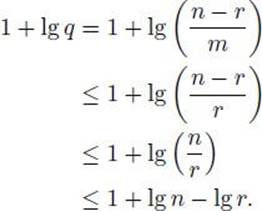
This last inequality along with Relation 11.9 establishes Bound 11.10. Owing to this bound, the total number of bit manipulations needed to compute all remainders in all recursive calls is bounded above by

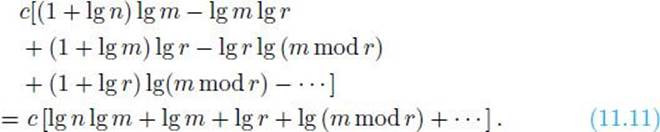
Relation 11.8 implies the number of recursive calls is bounded above by dt, where d is a constant greater than 0. This means the number of terms in Bound 11.11 is bounded above by dt. Therefore, since n > m > r > m mod r > · · · (where the dots denote the remaining terms in Bound 11.11), we conclude from Bound 11.11 that

• 11.2.2 An Extension to Euclid’s Algorithm

Theorem 11.1 entails that there are integers i and j such that

Knowledge of these integers will be important to our algorithm for solving modular linear equations in the next section. Next we modify Algorithm 11.1 to also produce these integers. In this version we make gcd a variable because so doing makes the proof of the correctness of the algorithm more transparent.

Algorithm 11.2

Euclid’s Algorithm 2

Problem: Compute the greatest common divisor of a positive integer and a nonnegative integer.

Inputs: a positive integer n and a nonnegative integer m.

Outputs: the greatest common divisor gcd of n and m, and integers i and j such that gcd = in + jm.

Algorithm 11.2 clearly has the same time complexity as Algorithm 11.1. So we need only prove it is correct. Before doing this, we show an example of applying it.

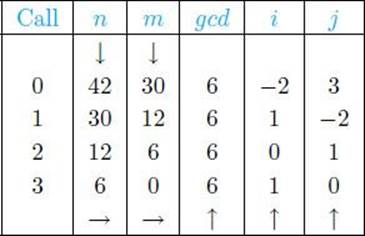
Example 11.18

Table 11.1 illustrates the flow of Algorithm 11.2 when the top-level call is

The values returned at the top level are gcd = 6, i = −2, and j = 3.

Next we prove Algorithm 11.2 is correct.

• Table 11.1 The values determined by Algorithm 11.2 when n = 42 and m = 30. The top-level call is labeled 0; the three recursive calls are labeled 1–3. The arrows show the order in which the values are determined.

Theorem 11.9

The values of i and j returned by Algorithm 11.2 are integers such that

Proof: The proof is by induction.

Induction base: In the last recursive call m = 0, which means the gcd(n, m) = n. Since the values of i and j are assigned values 1 and 0, respectively, in that call, we have that

Induction hypothesis: Assume in the kth recursive call the values determined for i and j are such that

Then the values returned by that call for i′ and j′ [to the (k − 1)st recursive call] are values such that

Induction step: We have for the (k − 1)st call that

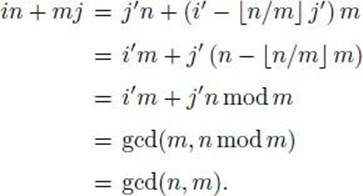
The second to the last equality is due to the induction hypothesis, and the last equality is owing to Theorem 11.3.

Notice that the value Algorithm 11.2 returns for j in the final recursive call can be any integer. We choose 0 for simplicity. Choosing a different integer yields a different (i, j) pair with the gcd(n, m) = in + jm.

11.3 Modular Arithmetic Review

We develop modular arithmetic within the context of group theory. So first we review that theory.

• 11.3.1 Group Theory

A closed binary operation ∗ on a set S is a rule for combining two elements of S to yield another element of S. We have the following definition:

Definition

A group G = (S, ∗) is a set S together with a closed binary operation ∗ on S satisfying the following:

1. * is associative. That is, for all a, b, c ∈ S

2. There is an identity element e in S. That is, for each a ∈ S

3. For each a ∈ S there exists an inverse element a′ such that

Example 11.19

The integers Z with addition constitute a group. The identity element is 0, and the inverse of a is −a.

Example 11.20

The nonzero real numbers with multiplication constitute a group. The identity element is 1, and the inverse of a is 1/a.

Example 11.21

Let S = (a, b, e) and assign

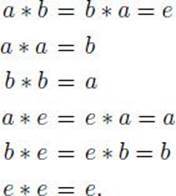
It is left as an exercise to show (S, ∗) is a group.

Can an element in a group have more than one inverse? The theorem that follows shows the answer is no.

Theorem 11.10

The inverse of each element in a group is unique.

Proof: Suppose a′ and a″ are both inverses of a. Then

However,

We conclude from the previous two equalities that a′ = a″.

Theorem 11.11

If there exists elements a and b in a group such that a ∗ b = a or b ∗ a = a, then b is the identity element e in the group.

Proof: If a ∗ b = a then

where a′ is the inverse of a. However,

Combining these two equalities proves this case. The other case is proved in the same way.

The last theorem establishes the result that the identity element in a group is unique.

A group G = (S, ∗) is said to be commutative (or abelian) if for all a, b ∈ S,

A group G = (S, ∗) is said to be finite if S contains a finite number of elements. The groups in Examples 11.19, 11.20, and 11.21 are all commutative, while only the one in Example 11.21 is finite.

• 11.3.2 Congruency Modulo n

We start with a definition.

Definition

Let m and k be integers and n be a positive integer. If n|(m − k) we say m is congruent to k modulo n, and we write

Example 11.22

Since 5|(33 − 18),

Recall m mod n gives the remainder when m is divided by n. The following theorem shows we can recognize congruence using the mod function.

Theorem 11.12

We have that m ≡ k mod n if and only if

Proof: The proof is left as an exercise.

Example 11.23

We already know 33 ≡ 18 mod 5. As the preceding theorem implies, 33 mod 5 = 18 mod 5 = 3.

The following theorem concerning congruency will be needed in Section 11.7 when we develop the RSA cryptosystem.

Theorem 11.13

Suppose n₁, n₂, … , n_j are pairwise relatively prime and

Then for all integer m and k,

if and only if, for 1 ≤ i ≤ j,

Proof: Suppose, for 1 ≤ i ≤ j, that

Then there exist integers h₁, h₂, … , h_j such that

It is left as an exercise to use Theorem 11.4 to show that this equality and the fact that n₁, n₂, … , n_j are pairwise relatively prime implies

where c is an integer. We then have

Since c is an integer, this means m ≡ k mod n.

In the other direction, if m ≡ k mod n, then there is an integer h such that

Therefore,

which means, for each i, m−k is a multiple of n_i. This completes the proof.

Example 11.24

The integers 2, 5, and 9 are pairwise relatively prime, and

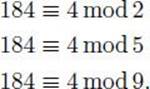
Since 2 × 5 × 9 = 90, the previous theorem implies

Next we show congruency modulo n is an equivalence relation.

Theorem 11.14

For any positive integer n, congruency modulo n is an equivalence relation on the set of all integers. That is,

1. (reflexivity)

2. (symmetry)

3. (transitivity)

Proof: The proof is left as an exercise.

The set of all integers congruent to m modulo n is called the equivalence class modulo n containing m. Since congruency is an equivalence relation, any integer in a given class determines the class. For a given integer m, it is the set

Example 11.25

The equivalence class modulo 5 containing 13 is

We denote the equivalence class modulo n containing m by [m]_n. So the equivalence class in the preceding example is denoted [13]₅. It can also be denoted [3]₅, [8]₅, and so on. Usually we denote an equivalence class using the smallest nonnegative integer in the class. So the equivalence class in the preceding example is usually denoted [3]₅. The set of all equivalence classes modulo n is denoted Z_n. That is,

Example 11.26

We have

For two members of Z_n we define addition as follows:

For this definition to make sense, the result must not depend on which members of [m]_n and [k]_n we choose. We show that next. We need to show that if

To that end, there exists integers i and j such that

So

which means s + t ∈ [m + k]_n.

Example 11.27

We have

Theorem 11.15

For every positive integer n_, (Z_n, +) is a finite commutative group.

Proof: The associativity and commutivity of + follows readily from the associativity and commutivity of + for the integers. The identity element is [0]₅. The additive inverse of [m]_n is [n − m]_n = [−m]_n since

Example 11.28

Consider the group (Z₅, +). Recall

The additive inverse of [1]₅ is [5 − 1]₅ = [4]₅. Note that

Similarly, the additive inverse of [2]₅ is [3]₅. Note that

For two members of Z_n we define multiplication as follows:

For this definition to make sense, the result must not depend on which members of [m]_n and [k]_n we choose. We need to show that if

It is left as an exercise to show this.

Example 11.29

We have

Now (Z_n, ×) is not always a group because there exists n (namely nonprimes) for which not every element in Z_n has a multiplicative inverse. That is, if we let [1]_n be the identity element, there exists [m]_n such that there is no k for which [m]_n × [k]_n = [1]_n.

Example 11.30

Consider

Suppose [6]₉ has a multiplicative inverse [k]₉. Then

which means there exists an integer i such that

Therefore, Theorem 11.2 implies 1 is the gcd(6, 9), which clearly is not the case.

The problem in the previous example is that 6 and 9 are not relatively prime. It seems if we include only numbers relatively prime to n, we will have a group. The next theorem proves this is so. First we develop notation for this set. Let

Clearly if n is prime, then Z^∗n = Z_n − {[0]_n}. It is not hard to see that one member of [m]_n is relatively prime to n if and only if all members are. So we need only look at the first n − 1 integers to determine the members of Z^∗n.

Example 11.31

We have that

Theorem 11.16

For every positive integer n_, (Z^∗_n, ×) is a finite commutative group.

Proof: Owing to Corollary 11.2 any divisor of m×k must be either a divisor of m or of k. Therefore, if m and k are each relative prime to n, m × k is relatively prime to n, which means × is a closed binary operation on Z^∗n. The associativity and commutivity of × follows readily from the associativity and commutivity of × for the integers. The identity element is [1]_n. If m is relatively prime to n, Theorem 11.2 says there exists integers i and j such that

which means

So [j]_n is the inverse of [m]_n.

Example 11.32

For the group (Z^∗₉, ×), we have the following multiplicative inverses:

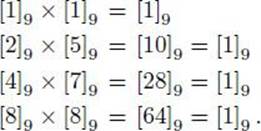
Theorem 11.17

The number of elements in Z^∗n is given by Euler’s totient function, which is

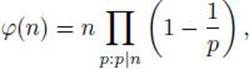
where the product is over all primes that divide n, including n if n is prime.

Proof: The proof can be found in Graham et al. (1989).

Note, if p is prime, that

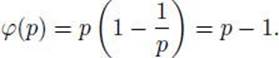
Example 11.33

The number of elements in Z^*₉ is

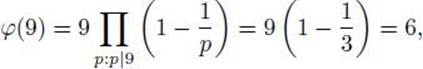
which can be verified by counting in Example 11.31.

Example 11.34

The number of elements in Z^∗₆₀ is

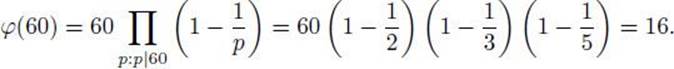
Example 11.35

Since 7 is prime, the number of elements in Z^∗₇ is

• 11.3.3 Subgroups

If G = (S, ∗) is a group, S′ ⊆ S, and G′ = (S′, ∗) is a group, then G′ is said to be a subgroup of G. It is called a proper subgroup if S′ ≠ S.

Example 11.36

For E, the set of even integers, and Z, the set of integers, (E, +) is a proper subgroup of (Z, +).

Before proceeding, we develop some useful notation. Given a group G = (S, ∗), and a ∈ S with inverse a′, for k > 0 we define

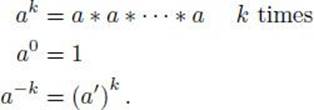
Suppose we have a group G = (S, ∗) and a subset S′ ⊆ S such that for every a, b ∈ S′, a ∗ b ∈ S′. Then S′ is said to be closed relative to ∗.

Theorem 11.18

Suppose we have a finite group G = (S, ∗), and a nonempty subset S′ ⊆ S, which is closed relative to ∗. Then (S′, ∗) is a subgroup of G.

Proof: Clearly, associativity holds. Let a ∈ S′. It is left as an exercise to show that since G is finite, there exist integers k, m ≥ 1 such that

Multiplying both sides of this equality by the inverse of a^k yields

where e is the identity element. Since S′ is closed, this means e is in S′. Next we show the inverse of every a ∈ S′ is in S′. As just shown, for every such a there is an m such that e = a^m. If m = 1, a = e, which means the inverse of a is e, and we already know e is in S′. Otherwise,

which means a^m−1 is the unique inverse of a. However, since S′ is closed, a^m−1 is in S′. This completes the proof.

Theorem 11.19

(Lagrange) Suppose we have a finite group G = (S, ∗), and a subgroup G′ = (S′, ∗) of G. Then

where |S| denotes the number of elements in S.

Proof: The proof can be found in Jacobson (1951).

Example 11.37

Consider the group (Z₁₂, +). It is left as an exercise to show that if

then (S′, +) is a subgroup of (Z₁₂, +). We have |S′| = 4, |Z₁₂| = 12, and 4|12 as the previous theorem implies.

Corollary 11.3

If G′ = (S′, ∗) is a proper subgroup of G = (S, ∗), then

Proof: The proof follows immediately from the preceding theorem.

Suppose we have a finite group G = (S, ∗), and a ∈ S. Let

Clearly, ⟨a⟩ is closed under ∗. So, because of Theorem 11.18, (⟨a⟩, ∗) is a subgroup of G. This group is called the subgroup generated by a. If the subgroup generated by a is G, we call a a generator of G.

Example 11.38

Consider the group (Z₆, +). We have

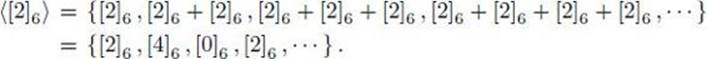
The previous example illustrates that once we obtain the identity element when generating the subgroup, we can stop because we will only repeat items already generated. The next theorem obtains this result. First we need a definition. Given a group, the order of group element a, denotedord(a), is the least positive integer t such that a^t = e, where e is the identity element.

Theorem 11.20

Suppose we have a finite group G = (S, ∗) and a ∈ S. Let t = ord(a). Then the subgroup ⟨a⟩ generated by a consists of the following t distinct elements:

Proof: First we show these elements are distinct. Suppose for 1 ≤ k < j ≤ t we have

Since j > k,

where i ≥ 1: Owing to these last two equalities and Theorem 11.11, we have aⁱ = e. Since i < t, we have a contradiction. Next we show there are no other elements in this subgroup. If k > t, then there exist positive integers q and r such that

We then have

If r = 0, a^r = e = a^t; otherwise 1 ≤ r < t. This completes the proof.

Owing to the previous theorem, we have

where t = ord(a), Note that the number of elements in ⟨a⟩ is ord(a).

Example 11.39

Consider the group (Z₆, +). We have

and

Clearly,

So [1]₆ is a generator of Z₆.

Example 11.40

Consider the group (Z^∗9, ×). Recall

We have

It is left as an exercise to show that

So [2]₉ is a generator of Z^∗9.,

Example 11.41

Consider the group (Z^∗7, ×). Recall that

We have

Corollary 11.4

Suppose we have a finite group G = (S, *) and a ∈ S. Let t = ord(a). Consider the sequence

Two elements aⁱ and a^j in this sequence are equal if and only if

This implies the sequence is cyclic with period t, and t is the smallest period for the sequence. That is, for 0 ≤ k < t and all i ≥ 0,

and t is the smallest number with this property.

Proof: The proof follows from the previous theorem and is left as an exercise.

Example 11.42

Consider the group (Z^∗5, ×). This table shows the powers of [4]₅:

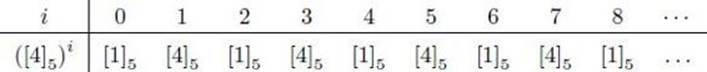
whereas this table shows the powers of [3]₅:

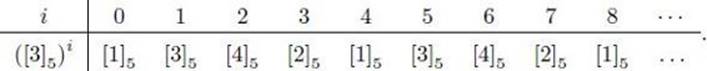
In this group, ord([4]₅) = 2 and ord([3]₅) = 4. Note the cyclical nature of the powers relative to these orders as implied by Corollary 11.4. Note further that [3]₅ is a generator of Z^∗₅.

Corollary 11.5

Suppose we have a finite group G = (S, ∗) with identity element e. Then for all a ∈ S,

where |S| denotes the number of elements in S.

Proof: From Theorem 11.20, the number of elements in the subgroup ⟨a⟩ generated by a is ord(a). Therefore, from Theorem 11.19, |S| = ord(a) × k for some integer k, and so

which completes the proof.

Theorem 11.21

(Euler) For any integer n > 1, for all [m]_n ∈ Z^∗_n,

Proof: The proof follows immediately from Theorem 11.17 and Corollary 11.5.

Example 11.43

Consider the group (Z^∗20, ×). We have that

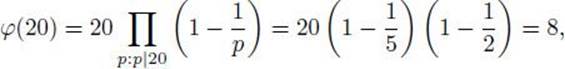
and

as the previous theorem implies.

Theorem 11.22

(Fermat) If p is prime, then for all [m]_p ∈ Z^∗_p,

Proof: The proof follows from the previous theorem and the fact that ϕ(p) = p − 1 if p is prime.

Example 11.44

Consider the group . We have that

as the previous theorem implies.

11.4 Solving Modular Linear Equations

Next we discuss solving the modular equation

for x, where x is an equivalence class modulo n, and m, n > 0. We will apply this result in Section 11.7 when we develop the RSA cryptosystem.

Let ⟨[m]_n⟩ be the subgroup generated by [m]_n relative to the group (Z_n+). Since ⟨[m]_n⟩= {[0]_n, [m]_n, [2m]_n,…}, Equation 11.12 has a solution if and only if

Example 11.45

Consider the group (Z₈, +). Since

the equation

has a solution if and only if [k]₈ is [0]_8, [6]_8, [4]₈, or [2]₈. For example, solutions to

are x = [2]₈ and x = [6]₈.

The following theorem tells us precisely the elements of the set ⟨[m]_n⟩

Theorem 11.23

Consider the group (Z_n, +). For any [m]_n Z_n, we have that

where d = gcd(n, m). This means

Proof: First show ⟨[d]_n⟩ ⟨[m]_n⟩. Owing to Theorem 11.2, there exists integers i and j such that

Owing to the previous equality, for any integer k,

which means [kd]_n = [kim]_n, and therefore [kd]_n ⟨[m]_n⟩, We conclude that ⟨[d]_n⟩ ⟨[m]_n⟩.

Next show ⟨[m]_n⟩ ⟨[d]_n⟩. Since d|m, there is an integer i such that m = id. Therefore, for any integer k,

which means [km]_n ⟨[d]_n⟩. We conclude ⟨[m]_n⟩ ⟨[d]_n⟩.

The final result follows from the results just established and Theorem 11.20.

Corollary 11.6

The equation

has a solution if and only if d|k, where d = gcd(n, m).

Furthermore, if the equation has a solution, it has d solutions.

Proof: As mentioned at the beginning of this section, the equation has a solution if and only if

Since Theorem 11.23 implies

this means the equation has a solution if and only d|k′ for some k′ [k]_n. Since [k]_n is an equivalence class modulo n and d|n, clearly d|k′ for one k′ [k]_n if and only if it does so for all members of [k]_n. This proves the first part of the corollary.

As to the second part, according to Theorem 11.23, ord([m]_n) = n/d. Therefore, owing to Corollary 11.4, the sequence

has period n/d and the first n/d items are distinct. This means, if [k]_n ⟨[m]_n⟩, that [k]_n appears exactly d times in the set

Clearly, each of these appearances is owing to a different member of Z_n. This completes the proof.

Corollary 11.7

The equation

has a solution for every equivalence class [k]_n if and only if gcd(n, m) = 1 Furthermore, if this is the case, each [k]_n has a unique solution.

Proof: The proof follows immediately from Corollary 11.6.

Corollary 11.8

The equivalence class [m]_n has a multiplicative inverse modulo n if and only if gcd(n, m) = 1. That is, the equation

has a solution if and only if gcd(n, m) = 1. Furthermore, if it has an inverse, that inverse is unique.

Proof: The proof follows immediately from Corollary 11.6. The uniqueness actually also follows from Theorem 11.16.

Example 11.46

Consider the group (Z₈, +). Since gcd(8, 6) = 2, according to Theorem 11.23,

which agrees with our result in Example 11.45. Owing to Corollary 11.6, the equation

has exactly two solutions when [k]₈ is any member of ⟨[6]₈⟩. In Example 11.45, we noted the two solutions when [k]₈ = [4]₈ are x = [2]₈ and x = [6]₈.

Example 11.47

Consider again the group (Z₈, +). Since gcd(8, 5) = 1, according to Theorem 11.23,

According to Corollary 11.7, the equation

has exactly one solution when [k]₈ is any member of ⟨[5]₈⟩. For example, when [k]₈ = [3]₈, the solution is x = [7]₈.

Example 11.48

Consider Z₉. Since gcd(9, 6) = 3, Corollary 11.8 implies [6]₉ does not have a multiplicative inverse modulo 9. Since gcd(9, 5) = 1, Corollary 11.8 implies [5]₉ does have a multiplicative inverse modulo 9. That inverse is [2]₉.

Theorem 11.24

Let d = gcd(n, m) and let i and j be integers such that

(We know from Theorem 11.2 that such i and j exist.) Suppose further d|k. Then the equation

has solution

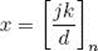
Proof: Owing to Equality 11.13, we have

Since is an integer, we can multiply both sides of this equality by , yielding

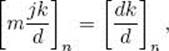
which means

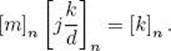
This proves the theorem.

Example 11.49

Consider the equation

We have gcd(8, 6) = 2,

and 2|4. Therefore, the previous theorem implies the equation

has solution

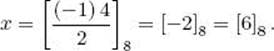
Theorem 11.25

Suppose the equation

is solvable, x = [j]_n is one solution, and d = gcd(n, m). Then the d distinct solutions of this equation are

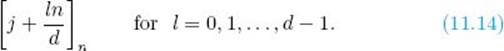
Proof: Owing to Corollary 11.6, there are exactly d solutions. Clearly,

So the d modulo classes in Expression 11.14 are all distinct. We complete the theorem by showing each of these classes is a solution to the equation. Since [j]_n is a solution of

Therefore, for l = 0, 1, · · ·, d − 1,

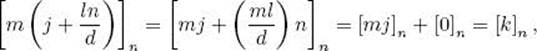
which means is also a solution to the equation.

Example 11.50

In Example 11.49, we showed that one solution of

is [6]₈. Since gcd(8, 6) = 2, the previous theorem implies the other solution is

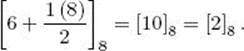
Corollary 11.6, Theorem 11.24, and Theorem 11.25 enable us to write a simple algorithm for solving modular linear equations. That is, we first employ Corollary 11.6 to see if a solution exists. If one does, we then use Theorem 11.24 to find one solution and Theorem 11.25 to find the other solutions. The algorithm follows:

Algorithm 11.3

Solve Modular Linear Equation

Problem: Find all solutions to a modular linear equation

Inputs: positive integers m and n, and integer k.

Outputs: if the equation [m]_n x = [k]_n is solvable, all solutions to it.

The input size in Algorithm 11.3 is the number of bits it takes to encode the input, which is given by

The time complexity includes the time complexity of Algorithm 11.2 (Euclid’s Algorithm 2), which we already know is O(st), plus the time complexity of the for-l loop. Since d can be as large as m or n, this time complexity is worst-case exponential in terms of the input size. However, we can do nothing about this since the problem requires that we compute and display an exponential number of values in the worst case.

11.5 Computing Modular Powers

For an element [m]_n Z_n and nonnegative integer k, the problem of computing

is called the problem of computing modular powers. Examples 11.43 and 11.44 showed the computation of some modular powers. Another example follows.

Example 11.51

Consider Z₂₀. We have

In Example 11.51 we determined the power simply by taking 7 to the 11th power. Clearly, this method has exponential time complexity in terms of the input size (approximately the logarithms of the numbers). Next we develop a more efficient algorithm.

The algorithm requires we represent k as a binary number. Let

be the ordered set of binary digits in that representation. For example, since the binary representation of 13 is 1101, if k = 13,

The algorithm now follows. We say that the algorithm uses the method of repeated squaring. The reason is obvious.

Algorithm 11.4

Compute Modular Power

Problem: For an element [m]_n Z_n and nonnegative integer k, compute ([m]_n)^k.

Inputs: positive integer n, and nonnegative integers m and k.

Outputs: ([m]_n)^k.

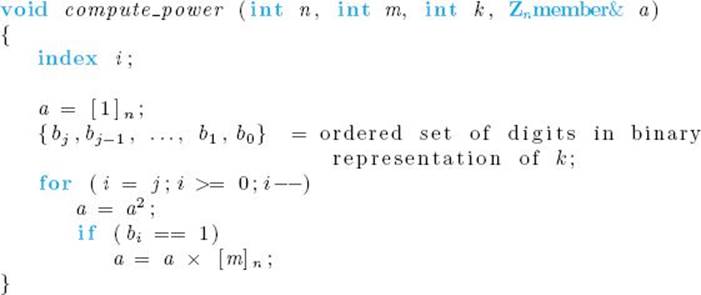
Next we show an example of applying Algorithm 11.4.

Example 11.52

Suppose

Since the binary representation of 45 is 101101,

Table 11.2 shows the state of a after each iteration of the for-i loop in Algorithm 11.4 given this input. The final value of a, namely [147]₂₅₇, is the value of ([5]₂₅₇)⁴⁵.

In Table 11.2, k_i is the value determined by the high-order j − i + 1 bits in the binary representation of k. That is,

• Table 11.2 The state of a after each iteration of the for-i loop in Algorithm 11.4 when n = 257, m = 5, and k = 45. The third row shows the value determined by the high-order j − i + 1 bits in the binary representation of k.

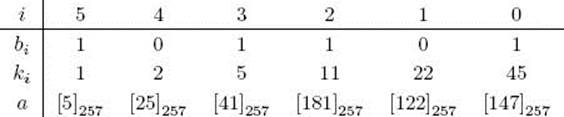
For example,

Clearly, k₀ = k. We will use these variables to prove the correctness of the algorithm, which we do next.

Theorem 11.26

After each iteration of the for-i loop in Algorithm 11.4,

Since k₀ = k, this means the final value of a is ([m]_n)^k.

Proof: The proof is by induction.

Induction base: We assume a minimal binary representation; so the high-order bit b_j equals 1. Therefore,

Before entering the for-i loop, a = [1]_n. Since b_j equals 1, the if condition is true in the first iteration, which means the instruction a = a × [m]_n executes. Therefore, we have

after the first iteration.

Induction hypothesis: Suppose after the iteration with index value i that

Induction step: We need to show that, after the iteration with index value (i − 1),

There are two cases: If b_i−1 = 0, clearly

Since the condition in the if statement is false, only the instruction a = a² changes the value of a. Since by the induction hypothesis the previous value of a is ([m]_n)^ki, we have

after this iteration.

If b_i−1 = 1, clearly

Since the condition in the if statement is true, the instruction a = a×[m]_n also executes. So in this case,

after this iteration.

It is straightforward that, if we let s be the number of bits it takes to encode the input, the time complexity of Algorithm 11.4 is in O(s³).

11.6 Finding Large Prime Numbers

Finding large prime numbers is necessary to the success of the RSA public-key cryptosystem, which is discussed in Section 11.7. After discussing searching for a large prime number, we show an algorithm for testing whether a number is prime.

• 11.6.1 Searching for a Large Prime

To find a large prime number, we randomly select integers of the appropriate size and test whether each selected integer is prime until one is found to be prime. When we use this method, an important consideration is the likelihood of finding a prime when an integer is chosen at random.

The prime distribution theorem, which we give next, enables us to approximate this likelihood.

The prime distribution function π(n) is the number of primes that are less than or equal to n. For example, π(12) = 5 since there are five primes, namely 2, 3, 5, 7, and 11, that are less than or equal to 12. The prime number theorem shown in Theorem 11.27, gives an approximation of π(n).

Theorem 11.27

We have that

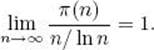
Proof: The proof can be found in Hardy and Wright (1960).

Owing to the previous theorem, for large values of n we can use n/ ln n as an estimate of the number of primes less than or equal to n. Therefore, if we randomly choose an integer between 1 and n according to the uniform distribution, the probability of it being prime is about

Example 11.53

If we randomly choose an integer between 1 and n = 10¹⁶ according to the uniform distribution, the probability of it being prime is about

Suppose we choose 200 such numbers at random. The probability of them all not being prime is then about

Example 11.54

If we randomly choose an integer between 1 and n = 10¹⁰⁰ according to the uniform distribution, the probability of it being prime is about

Suppose we choose 200 such numbers at random. The probability of them all not being prime is then about

As noted at the beginning of this section, to find a large prime number we randomly select numbers in the appropriate range, and we then check them for being prime until one is found to be prime. We see from the previous examples that it should not take very long (relative to the size of the numbers in the range) to find a prime. Next we discuss how we check whether a number is prime.

• 11.6.2 Checking if a Number Is Prime

At the beginning of Section 9.2 we showed a straightforward algorithm for determining if a number is prime. However, as discussed in that section, the algorithm has exponential-time complexity in the worst case. So it cannot be used to check large numbers. Note that this inefficient algorithm finds a factor of the number if it is composite. So the algorithm can be used (repeatedly) to factor a number.

Until recently no one had ever found a polynomial-time algorithm for the prime-checking problem, and many thought it to be NP-complete. The standard efficient algorithm for prime-checking was a Monte Carlo algorithm called the Miller-Rabin Randomized Primality Test, which appeared in Rabin (1980). If a number is prime, then this algorithm says the number is always prime. However, very rarely, the algorithm will declare a composite number to be prime. This happens so rarely, that the algorithm could essentially be counted upon for accuracy. The Miller-Rabin algorithm does not find a factor of the number if it determines the number is composite. So it cannot be used for factoring.

Finally, in 2002, Agrawal et al. succeeded in developing a polynomial-time algorithm for the prime-checking problem. That algorithm is described here.

A Polynomial-Time Algorithm

First we need further results from number theory.

Definition

Let f(x) and g(x) be polynomials with integral coefficients. If the coefficients of each power of x are congruent modulo n, we say that f(x) and g(x) are congruent modulo n, and we write

Example 11.55

We have

because

Example 11.56

We have

because

Missing powers are assumed to have coefficient 0.

Example 11.57

We have

because

Example 11.58

We have

because

This last example illustrates something interesting. Owing to Theorem 11.22, for all integers x,

but yet the polynomials x⁵ and x are not congruent modulo 5.

Next we show a theorem that gives a straightforward way to determine whether a number is prime. But first we need a lemma.

Lemma 11.2

If n is prime then for all integers m,

Proof: We have that

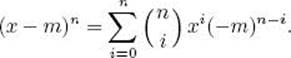
Therefore,

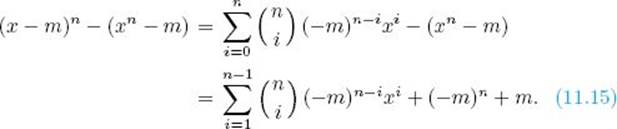
Since n is prime, clearly for 1 < i ≤ n − 1,

Therefore, for each i the coefficient of xⁱ in Equality 11.15 is congruent to 0 modulo n. So we only need to show

If n = 2

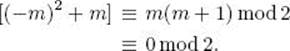
The last step is owing to the fact that either m or m + 1 is even. If n > 2, then n is odd and therefore

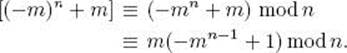
Now if m is a multiple of n, then m ≡ 0 mod n. Otherwise, owing to Theorem 11.22, (−mⁿ⁻¹ + 1) ≡ 0 mod n. This completes the proof.

Theorem 11.28

Suppose m and n are relatively prime. Then n is prime if and only if

Proof: Owing to Lemma 11.2, the congruence is satisfied if n is prime.

In the other direction, suppose n is composite. Let q be a factor of n and let k be the order of q in n. It is left as an exercise to show Since n is relatively prime to m, clearly q^k is relatively prime to (−m)^n−q. Therefore, does not contain q^k as a factor, which means it is not congruent to 0 modulo n. However, this expression is one of the coefficients in Equality 11.15. This completes the proof.

Example 11.59

The numbers 9 and 2 are relatively prime. As Theorem 11.28 implies,

since

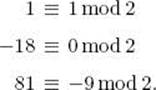
Example 11.60

The numbers 9 and 4 are relatively prime and 4 is not prime. Theorem 11.28 implies

It is left as an exercise to expand the exponent and illustrate this result.

Theorem 11.28 yields a straightforward algorithm for determining if a number is prime. That is, given an integer n, we choose an integer m relatively prime to n and determine whether Congruence 11.16 is satisfied. However, since we need to evaluate n + 1 coefficients in the left-hand side of Congruence 11.16, this algorithm has exponential time complexity. We do a ‘trick’ to improve on this. However, first we need more definitions.

As is the case for integers, the mod function returns the remainder when one polynomial is divided by the other. That is,

is the polynomial that is the remainder when f(x) is divided by g(x). The following example illustrates this idea.

Example 11.61

Since

then

Now suppose f(x), g(x), and h(x) are polynomials with integral coefficients. If

we write

Example 11.62

We have that

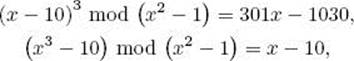
and

So

Example 11.63

We have that

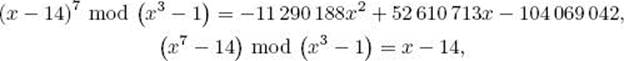
and

So

Example 11.64

We have that

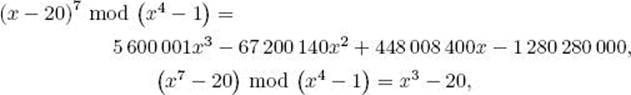
and

So

The previous examples illustrate the truth of the following theorem:

Theorem 11.29

Suppose n and r are prime. Then for all integers m,

Proof: The proof follows from Lemma 11.2 and is left as an exercise.

If the previous theorem said that n is prime if and only if Congruence 11.17 were satisfied, we would immediately be able to improve on using Congruence 11.16 to test whether a number was prime. That is, the computation of (xⁿ − m) mod(x^r − 1) is trivial, and Knuth (1998) develops an algorithm for computing (x − m)ⁿ mod (x^r − 1), which uses fast Fourier multiplication and whose time complexity is in . So, if Theorem 11.29 were ‘if and only if’ and r were small, we could fairly quickly replace the determination of Congruence 11.16 to that of a congruence involving far fewer coefficients. The following example illustrates this.

Example 11.65

Suppose we want to determine whether 11 is prime and Theorem 11.29 is ‘if and only if.’ Choose m = 4 and r = 3. We have

and

We now check whether

instead of checking whether

So we have reduced the problem of testing for 12 congruencies to that of testing for three.

The problem in this procedure is that Theorem 11.29 is not ‘if and only if’ even if we choose m relatively prime to n. That is, some composites will satisfy Congruence 11.17 for certain values of m and r, where m is relatively prime to n. So if we simply check whether the congruence is satisfied for particular values, a composite may pass the test. We solve this problem by choosing an appropriate r and checking for several values of m. In this way, no composites will be found to be prime, and we still have a polynomial-time algorithm. After presenting the algorithm, we obtain these results. Before we do this, we need some additional notation.

Recall that the order of group element a, denoted ord(a), is the least positive integer t such that a^t = e, where e is the identity element. Given the group is then the least positive integer t such that ([n]_r)^t = [1]_r. That is, it is the least positive integer such that

We call this the order of n modulo r and we denote it as ord_r(n).

Algorithm 11.5

Polynomial Determine Prime

Problem: Determine whether an integer is prime.

Inputs: an integer n > 1.

Outputs: if n is prime, true; if n is composite, false.

Correctness of the Algorithm

Next we prove the algorithm is correct. First we prove the algorithm always determines that a prime is prime.

Theorem 11.30

If a prime number is the input to Algorithm 11.5, the algorithm returns true.

Proof: If n is prime, then for all r < n,

which means false cannot be returned in the first while loop. Since n and r are prime, owing to Theorem 11.29, false cannot be returned in the second

while loop. We conclude the algorithm exits with the last instruction, and that instruction returns true.

It is more difficult to prove the algorithm always determines a composite number to be composite. We do that next. First we need the following two lemmas, which generalize Lemma 11.2 and Theorem 11.29.

Lemma 11.3

Suppose g(x) is a polynomial with integer coefficients and n is prime. Then

Proof: Let

Then

Furthermore, the coefficient of xⁱ in [g(x)]ⁿ is

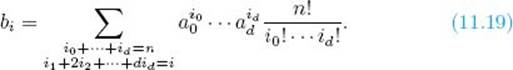
Case 1: i ≠ jn for any j. Then, as can be seen from Equality 11.18, the coefficient of xⁱ in g(xⁿ) is 0. Furthermore, as can be seen from Equality 11.19, i_j ≠ n for all j in all of the terms that comprise b_i. However, then n divides each term, which means n|b_i, and b_i ≡ 0 mod n. This proves this case.

Case 2: i = jn for some j where 0 ≤ j ≤ d. Then, as can be seen from Equality 11.18, the coefficient of xⁱ in g(xⁿ) is a_j. Furthermore, if we take i_j = n, we have ji_j = jn = i. Therefore, as can be seen from Equality 11.19, one of the terms in b_i is

For each of the other terms in b_i, clearly we will have i_k ≠ n for every k, which means n divides the term, and the term is congruent to 0 modulo n. This case now follows from the fact that Theorem 11.22 says

This completes the proof.

Lemma 11.4

Suppose g(x) is a polynomial with integer coefficients, and n and r are prime. Then

Proof: The proof follows from the previous lemma and is left as an exercise.

We also need the following lemmas:

Lemma 11.5

If r and q are prime, q divides r − 1, and q ≥ 4√rlg n, then q|ord_r(n) if and only if

Proof: If we let t = ord_r(n), then, owing to the fact that r is prime, Theorem 11.17, and Theorem 11.19, there exists an integer k such that r − 1 = tk. Since q divides r − 1 and q is prime, Corollary 11.2 implies q|t or q|k. Now we prove the ‘if and only if’:

Suppose and by way of contradiction, suppose q. Since q|t or q|k, this means q|k. Therefore, since r − 1 = tk, there exists an integer j such that r − 1 = tjq, which means (r − 1) /q = tj. However, then we have which means

This contradiction proves q|t.

In the other direction, suppose q divides t. Since q ≥ 4√rlgn,

Since t = ord_r(n), this means

which completes the proof.

Lemma 11.6

If n is composite, q is prime, and q divides q|ord_r(n), then there is a prime factor p of n such that

Proof: Let p₁, p₂,…, p_k be the prime factors of n. It is left as an exercise to show

where lcm is the least common multiple. Since q|ord_r(n) and q is prime, Theorem 11.7 implies there is some p_i such that q|ord_r(p_i). This completes the proof.

Our proof of the next theorem relies heavily on the following lemma. The proof of this lemma requires algebra that is beyond the scope of this text. For the reader familiar with abstract algebra, we present the results that prove this lemma at the end of this section. Now we merely state it.

Lemma 11.7

Suppose the second while loop in Algorithm 11.5 is exited because switch is true. If p is as in Lemma 11.6, and we let l = 2√rlg n, then there is a polynomial

with the following property: If we let

then

1. J_g(x) is closed under multiplication.

2. There is an integer such that for

then

Proof: See the end of this section.

We can now prove our main result.

Theorem 11.31

If a composite number is the input to Algorithm 11.5, the algorithm returns false.

Proof: If the number is composite and the first while loop is abruptly ended owing to the return statement in it, false is returned and we are done. If the first while loop is exited because r = n − 1, then n must be prime. So we will assume a composite is entered and the first while loop is exited because switch is true. Then, owing to Lemma 11.5, q divides ord_r(n). Suppose by way of contradiction that the algorithm returns true. Then, owing to the second while loop, for 1 ≤ m ≤ l = 2√rlg n,

which means

where p is as in Lemma 11.6. Therefore, each term (x−m) in g(x) in Lemma 11.7 individually satisfies Congruence 11.20, which means

Therefore, n J_g(x) where J_g(x) is as defined in Lemma 11.7. Furthermore, p J_g(x) owing to Lemma 11.4, and trivially 1 J_g(x).

Now consider the set

Owing to Part 1 of Lemma 11.7, E ∈ J_g(x). Furthermore,

Therefore, by the pigeonhole principle, there are two elements nⁱp ^j and n^hp^k in E with i ≠ h or j ≠ k such that

So, owing to Part 2 of Lemma 11.7, we have

where a is as in that lemma. Since p|n, n is composite, and i, j ≤ √r,

Similarly, since h, k ≤ √r,

However, since a > n²√^r/_2, Congruence 11.21 therefore implies

Since p|n and either i ≠ h or j ≠ k, this last equality implies for some integer s ≥ 1 that

However, in the first step of the algorithm we checked whether n is of the form p^s for s ≥ 2. Therefore, s = 1 and n is prime. This contradiction proves the theorem.

Time Complexity of the Algorithm

Next we discuss the time complexity of Algorithm 11.5. First we need some lemmas and a theorem.

Lemma 11.8

Let q_m be the largest prime factor of m. Then there exists a positive constant c and integer N such that for n > N

Proof: The proof can be found in Baker and Harman (1996).

Lemma 11.9

Let π(m) be the number of primes less than or equal to m. Then for m ≥ 1,

Proof: The proof can be found in Apostol (1997).

Lemma 11.10

Given positive integers m and n, the product

has at most m² lg n prime factors.

Proof: Each term has at most m lg n prime factors, and there are m terms.

Theorem 11.32

There exists positive constants c₁ and c₂ and integer N such that for every n > N there is a prime r in the interval

such that the largest prime factor q of r − 1 satisfies

Proof: For the moment, let c₁ and c₂ be arbitrary positive integers. Owing to Lemma 11.8. there exists a positive constant c and integer N such that for c₂ (lg n)⁶ > N,

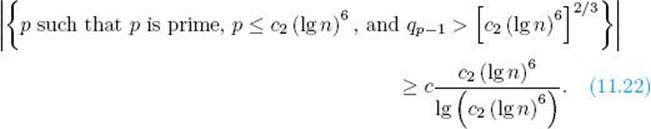
It is left as an exercise to show that Equality 11.22 implies

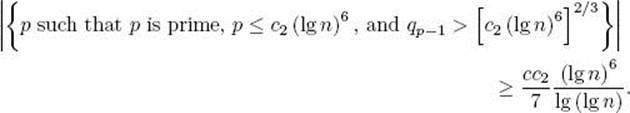
If we let m = c₁ (lg n)⁶ in Lemma 11.9, we obtain, after some manipulations, that the number of primes less than or equal to c₁ (lg n)⁶ is no greater than

Combining Inequalities 11.22 and 11.23, we obtain that the number of primes p in the interval

satisfying

is greater than or equal to

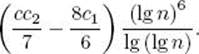
Call such primes special primes. Recall that c₁ and c₂ were arbitrary positive integers. Now choose c₁ ≥ 4⁶. We then have, for any special prime p,

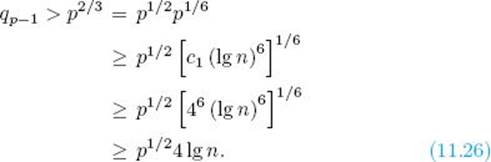
The first inequality is owing to Inequalities 11.24 and 11.25, and the second is owing to Inequality 11.25.

Now choose c₂ so that . We then have for n > N that the number of special primes is greater than or equal to

Now let x = c₂ (lg n)⁶. Then

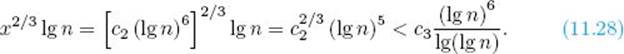
Owing to Lemma 11.10, the product

has at most x^2/3lg n prime factors. Therefore, due to Inequalities 11.27 and 11.28, there is at least one special prime r that does not divide .

We will show that r satisfies the conditions of the theorem. Clearly, r satisfies the first two conditions owing to Inequalities 11.24 and 11.26. So if we let q = q_r−1, we need only show

To that end, suppose

Then Therefore, since r does not divide , we only need to show

to obtain a contradiction. Since Inequality 11.25 says , we only need to show

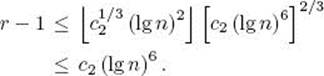
However, this last inequality does hold, due to Inequality 11.24. This contradiction completes the proof.

Analysis of Algorithm 11.5

Worst-Case Time Complexity (Polynomial Determine Prime)

Basic operation: one-bit manipulation.

Input size: the number of bits s it takes to encode n, which is given by

To determine whether n is of the form k^j, the number of roots checked is in O(s). That is, we need to check n^1/2, n^1/3,…, n^1/m, where m = lg n. Using the brute-force technique discussed in Section 2.6, the time complexity of checking each root is in O(s²). Therefore, the total time complexity of this determination is in

Owing to Theorem 11.32, the number of passes through the first while loop is in O(s⁶). Let’s discuss the work done in each pass. Since r < n, if we use Algorithm 11.1, the time complexity of the computation of the gcd(n, r) is in O(s²). Suppose we use the algorithm presented at the beginning of Section 9.2 to determine if r is prime and to find the largest prime factor of r − 1. There are at most r^1/2 passes through the while loop in that algorithm, and, using the brute-force technique discussed in Section 2.6, the time complexity of the computation of the remainder in each pass is in O(s²). Therefore, the total time complexity is in O(r^1/2s²), which means, owing to Theorem 11.32, that time complexity is in O(s³s²) = O(s⁵). Again using the techniques in Section 2.6, the time complexity of incrementing r and of checking the exit condition in the first while loop is in O(s²). Therefore, the total time complexity of the first while loop is in

Since r < c(lg n)⁶, it is possible to obtain a tighter bound than the one just developed. However, as we shall see, the second while loop dominates our final bound anyway.

The number of passes through the second while loop is in O(r^1/2s), which means, owing to Theorem 11.32, that the number of passes is in O(s³s) = O(s⁴). As we mentioned following Theorem 11.29, the time complexity of the congruence determination in that loop is in O(rs²) if we use Fast Fourier multiplication, which means, again owing to Theorem 11.32, that time complexity is in O(s⁶s²) = O(s⁸). Therefore, the total time complexity of the second while loop is in

We conclude that

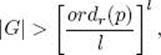
Agrawal et al. (2002) note that in practice Algorithm 11.5 might be much faster than the bound just obtained. Indeed, they prove that, if a conjecture they make is true, a heuristic time complexity for the algorithm is in O(s⁶).

Results that Prove Lemma 11.7

Next we state the lemmas that prove Lemma 11.7. The section requires knowledge of abstract algebra. First we explain our notation. Given a ring R, we denote the corresponding polynomial ring by R[x]. For example, the polynomial ring corresponding to Z_n is denoted by Z_n[x]. Given a ring Rand an ideal L in R, the factor ring consisting of the forms {r + l: l L} is denoted R/L. Furthermore, if r R, and L is the ideal consisting of all multiples of r, we denote R/L by R/r. For example, Z_n could be denoted by Z/n. As another example, given a polynomial ring R(x) and polynomial f(x) R(x), the factor ring determined by the ideal consisting of all multiples of f(x) is denoted R(x)/f(x). Given a prime p, we will be interested in the ring (actually field) Z_p, the polynomial ring Z_p[x], and the factor ring Z_p[x]/h(x).

We have the following lemmas, which we state without proof. The proofs use standard algebraic manipulations, can be developed in sequence, and can be found in Agrawal et al. (2002).

Lemma 11.11

Let p and r be prime with p ≠ r.

1. If h(x) is a factor of x^r − 1, and m ≡ k mod r, then

2. If we let ord_r(p) be the order of p modulo r, then (x^r − 1)/(x − 1) factors into polynomials, which are irreducible over Z_p and which have degree ord_r(p).

Suppose the second while loop in Algorithm 11.5 is exited because switch is true, p is as in Lemma 11.6, and we let l = 2√r lg n. Owing to Part 2 of the preceding lemma, there is a polynomial h(x), which is a factor of x^r − 1, is irreducible over Z_p, and has degree ord_r(p). The following lemmas all assume the second while loop in Algorithm 11.5 is exited because switch is true, p is as in Lemma 11.6, h(x) is the polynomial just described, and l = 2√r lg n.

Lemma 11.12

In Z_p[x]/h(x), let G be the group generated by the l binomials

That is,

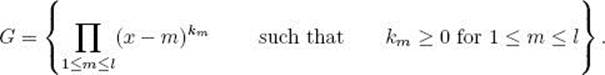
Then G is cyclic and

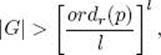
where |G| is the number of elements in G.

Lemma 11.13

Let G be the group in the previous lemma, g(x) be a generator of G, and a_g be the order of g(x) in Z_p[x]/h(x). Then

Proof: Since l = 2√r lg n and q ≥ 4√r lgn, we have q ≥ 2l. Since Lemma 11.6 says q|ord_r(p), this means ord_r(p) ≥ 2l. Owing to the previous lemma, we then have

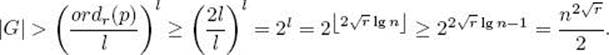
The proof now follows from the fact that g(x) is a generator of G.

Lemma 11.14

Let g(x) be as in the previous lemma. Then the set

is closed under multiplication.

Lemma 11.15

Let g(x), a_g, and J_g(x) be as in the previous lemmas. Then for all m, k J_g(x), if

then

It is straightforward that Lemma 11.7 follows from the preceding lemmas if we let a = a_g.

11.7 The RSA Public-Key Cryptosystem

Recall the situation discussed at the beginning of this chapter concerning Bob wanting to send Alice a secret love note over the Internet. We noted that if he could encode the message so that it appears as gibberish and only Alice could decode the gibberish back to the original message, he would not need to fear his friends intercepting the message. Public-key cryptosystems enable Bob to do this. After describing such systems, we present the RSA public-key cryptosystem.

• 11.7.1 Public-Key Cryptosystems

A public-key cryptosystem consists of a set of permissible messages, a set of participants such that each participant has a public key and a secret key, and a network for sending messages among the participants. The set of permissible messages might include all character sequences of some given length or less. If we let

then each participant x’s public key pkey_x and secret key skey_x determine functions pub_x and sec_x, respectively, from M to M, which are inverses of each other. That is, for each b M

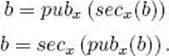
Now the public keys of all participants are known to all the participants, but the secret key of x is known only to x. So, for example, if Bob wants to send Alice a secret love note b, he and Alice do the following:

1. Bob computes c = pub_Alice(b) using Alice’s public key, pkeyAlice. The message c is called ciphertext. It is unreadable.

2. Bob sends ciphertext c to Alice.

3. Alice computes b = secAlice(c) using her secret key skeyAlice.

Example 11.66

Suppose Bob wants to send Alice the message ‘I love you.’ The steps are as follows:

1. Bob computes

Suppose the result is ‘@!##% * (!’.

2. Bob sends this message to Alice. Bob’s friends see ‘@!##% * (!’.

3. Alice computes

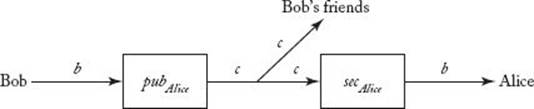
The application of pub_Alice in Step 1 is called encryption, while the application of secAlice in Step 3 is called decryption. These steps are illustrated in Figure 11.1. Note that since only Alice knows secAlice, only she can decode the ciphertext c back to the original message b. So Bob’s friends see only the ciphertext.

This method will work as long as it is not possible (or at least it is very difficult) to determine skey_x from pkey_x. Next we show a system that makes it very difficult to do so.

Figure 11.1 Bob encrypts his message b using Alice’s public key, and Alice decrypts it using her secret key. Bob’s friends see only the ciphertext c.

• 11.7.2 The RSA Cryptosystem

The RSA cryptosystem relies on the facts that we can find large primes fairly readily, but we have no efficient method for factoring a large number. After presenting the method, we discuss these facts further.

The System

In the RSA public-key cryptosystem, each participant creates his public key and secret key according to the following steps:

1. Select two very large prime numbers, p and q. The number of bits needed to represent p and q might be 1024.

2. Compute

The formula for ϕ(n) is owing to Theorem 11.17.

3. Select a small prime number g that is relatively prime to ϕ(n).

4. Using Algorithm 11.3, compute the multiplicative inverse [h]_ϕ(n) of [g]_ϕ(n). That is,

Owing to Corollary 11.8, this inverse exists and is unique.

5. Let pkey = (n, g) by the public key, and skey = (n, h) be the secret key.

The set of permissible messages is Z_n. The function corresponding to the public key pkey = (n, g) is

where b Z_n, and the function corresponding to the secret key skey = (n, h) is

The values of these functions can be computed using Algorithm 11.5.

For this system to be correct, the functions corresponding to the public and secret keys must be inverses of each other. Next we prove this is the case.

Theorem 11.33

The functions in Equalities 11.29 and 11.30 are inverses of each other.

Proof: Owing to Equalities 11.29 and 11.30, for any b Z_n

So we need to show only that

To that end, let m b. (Recall b Z_n.) Then m^gh b^gh. We will show

Since g and h are multiplicative inverses modulo ϕ(n) = (p − 1)(q − 1),

which means there is an integer k such that

There are two cases.

Case 1: Assume [m]_p ≠ [0]_p. We then have

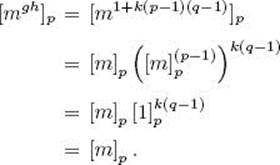
The third equality above is due to Theorem 11.22.

Case 2: If [m]_p = [0]_p,

So we’ve established Equality 11.31. Similarly,

Owing to Equalities 11.31 and 11.32,

and

Due to Theorem 11.13, we therefore have

which means

This completes the proof.

Discussion

As mentioned previously, the success of the RSA cryptosystem relies on the facts that we can find large primes fairly readily, but we have no efficient method for factoring a large number. That is, we can find a large prime as follows. First, we randomly choose integers of the appropriate size. As discussed at the beginning of Section 11.6.1, it should not take very long even to find a fairly large prime. For each integer chosen, we can then use Algorithm 11.5, which is polynomial-time, to check whether the number is prime. We do this until we find two large primes. As discussed in Section 11.6.2, even before Algorithm 11.5 was developed, the Miller-Rabin Randomized Primality Test was used to efficiently check with a very low error rate whether a number was prime. Indeed, the Miller-Rabin Randomized Primality Test may still be the algorithm of choice for prime checking since its time complexity is in O(es³), where s is the number of bits it takes to encode the input, and e is an integer chosen such that the probability the algorithm makes an error is no greater than 2^−e. So if we choose e to be only 40, the probability of an error is no greater than 2⁻⁴⁰ = 9. 094 9 × 10⁻¹³.

On the other hand, no one has ever found a polynomial-time algorithm for factoring a number. The possibility exists that one could find the value of h in the secret key skey = (n, h) without factoring n. However, no one has found an efficient way to do this either. Currently we can achieve security with the RSA cryptosystem if integers containing around 1024 or more bits are used.

EXERCISES

Section 11.1

1. Find the positive divisors of the following integers.

(a) 72

(b) 31

(c) 123

2. Prove that if h|m and m|n, then h|n.

3. Show that two integers divide each other if and only if they are equal.

4. Let p and q be two prime numbers. If p = q + 2, then p and q are called “twin prime numbers.” Find two pairs of twin prime numbers.

5. Prove that gcd(n, m) = gcd(m, n).

6. Prove that if m and n are both even, then gcd (m, n) = 2 gcd (m/2, n/2).

7. Prove that if n ≥ m > 0, then gcd (m, n) = gcd (m, n − m).

8. Prove that if p is a prime number and 0 < h < p, then gcd(p, h) = 1.

9. Use Corollary 11.2 to show that the prime factorization of an integer, as discussed in Theorem 11.5, is unique.

10. Write each of the following integers as a product of prime numbers.

(a) 123

(b) 375

(c) 927

11. Prove Theorem 11.6.

12. Prove Theorem 11.7.

13. Prove that for positive integers m and n, gcd(m, n) = lcm(m, n) iff m = n.

Section 11.2

14. Illustrate the flow of Algorithm 11.1 when the top-level call is gcd (68, 40).

15. Write an iterative version of Algorithm 11.1. Your algorithm should only use a constant amount of memory [i.e., the space complexity function is in θ(1)].

16. Write an algorithm that uses Algorithm 11.1 to express a rational number in its lowest terms. You may assume that this rational number is given in the form of a fraction m/n where m and n are integers.

17. Illustrate the flow of Algorithm 11.2 when the top-level call is Euclid (64,40,gcd,i,j).

18. Write an algorithm that uses subtraction to compute the greatest common divisor. (See Exercise 7.) Analyze your algorithm.

Section 11.3

19. Show that (S, *) of Example 11.21 is a group.

20. Prove Theorem 11.12.

21. The following was left as an exercise in the proof of Theorem 11.13. Show that there exists an integer c such that h₁ = cn₂n₃ · · · n_j.

22. Prove Theorem 11.14.

23. Show that if s [m]_n and t [k]_n, then s × t [m × k]_n.

24. Show that if G=(S, *) is a finite group and a S, then there exists integers k,m ≥ 1 such that a^k = a^ka^m.

25. Show that if S={[0]₁₂,[3]₁₂,[6]₁₂,[9]₁₂}, then (S,+) is a subgroup of (Z₁₂,+).

26. Use Theorem 11.19 to prove Corollary 11.3.

27. Consider the group . Show that .

Section 11.4

28. Solve the following modular equations.

(a) [8]₁₀ x = [4]₁₀ (b) [4]₁₇ x ≡ [5]₁₇

29. Implement Algorithm 11.3 and run it on various problem instances.

30. Find all solutions to the equations [1]₇ x = [3]₇ and [12]₉ x = [6]₉.

Section 11.5

31. Compute ([3]₇₃)¹² by raising 3 to the 12^th power.

32. Compute ([7]₇₃)¹⁵ by raising 7 to the 15^th power.

33. Use Algorithm 11.4 to compute ([3]₇₃)¹².

34. Use Algorithm 11.4 to compute ([7]₇₃)¹⁵.

35. Implement Algorithm 11.4, and run it on various problem instances.

Section 11.6

36. Find the number of prime numbers that are less than or equal to 100.

37. If an integer between 1 and 10,000 is randomly chosen according to the uniform distribution, approximately what is the probability of it being prime?

38. Suppose we randomly choose 100 numbers between 1 and 10,000 according to the uniform distribution. Approximately, what is the probability of all of them not being prime?

39. Show that if n is prime and 1 < k ≤ n − 1, then B(n,k) ≡ 0 mod n, where B(n,k) denotes the binomial coefficient.

40. Show that if q is a factor of n and k is the order of q in n, then q^k where B(n,q) denotes the binomial coefficient.

41. Are 9x³ + 2x and x²− 4 congruent modulo 2?

42. Show that (x − 9)⁴ is not congruent to (x⁴ − 9) modulo 4.

43. Show that (x − 5)³ is congruent to (x³ − 5) modulo 3.

44. Prove Theorem 11.29.

45. Implement Algorithm 11.5 and run it on different problem instances.

46. Use Lemma 11.3 to prove Lemma 11.4.

47. The following was left as an exercise in the proof of Lemma 11.6. Show ord_r(n)|lcm(ord_r(p₁), ord_r(p₂),…,ord_r(p_k)).

48. Use Inequality 11.22 to obtain the inequality that follows it.

Section 11.7

49. What is the difference between a public key and a secret key?

50. Consider an RSA cryptosystem using p = 7, q = 11 and g = 13.

(a) Compute n.

(b) Compute ϕ.

(c) Find h.

51. Consider an RSA cryptosystem using p = 23, q = 41 and g = 3. Encipher the message [847]₉₄₃.

52. Use the RSA cryptosystem of Exercise 51 to decrypt the encrypted message found in that exercise.

53. In an RSA cryptosystem, show that if ϕ(n) can be discovered, then the cryptosystem may be compromised.

Additional Exercises

54. Prove that there are infinitely many prime numbers.

55. Show that the gcd operator is associative. That is, for all integers m, n, and h, we have gcd (m, gcd(n, h)) = gcd (gcd(m, n),h).

56. Prove that if m is odd and n is even, then gcd (m, n) = gcd (m, n/2).

57. Prove that if m and n are both odd, then gcd (m, n) = gcd ((m − n)/2, n). 58. Find the necessary condition to have equation mx ≡ my mod n imply x ≡ y mod n.

59. Assuming that p is a prime number, find the solutions of the equation x² = [1]_p.

60. In an RSA cryptosystem, let p and q be the large primes, let n = pq, and let pub be the public key. Show that pub(a)pub(b) is congruent to pub(ab) modulo n.