Knowledge-based Configuration: From Research to Business Cases, FIRST EDITION (2014)
Part III. Advanced Topics
Chapter 12. Redundancy Detection in Configuration Knowledge
Alexander Felferniga, Florian Reinfranka, Gerald Ninausa and Paul Blazekb, aGraz University of Technology, Graz, Austria, bcyLEDGE, Vienna, Austria
Abstract
Configuration systems exploit a knowledge base for determining solutions of interest for the user. The development and maintenance of such knowledge bases is a time-consuming and error-prone task. For example, redundant constraints are specified that often increase both the effort for calculating a solution and efforts related to knowledge base development and maintenance. In this chapter we present two alternative algorithms that can be exploited for the determination of minimal cores (minimal nonredundant constraint sets). The first algorithm (SEQUENTIAL) is the better choice for centralized scenarios where the degree of redundancy is low. The second one (COREDIAG) is especially useful for distributed knowledge engineering scenarios where the degree of redundancy can become high.
Keywords
Knowledge-based Configuration; Redundancy Detection; Knowledge Engineering
Acknowledgments
The work presented in this chapter was partially funded by the Austrian research promotion agency (grant number: 827587).
12.1 Introduction
The central element of a constraint-based application is a knowledge base (constraint set). When developing and maintaining constraint sets, users are often defining faulty constraints (the system calculates solutions that are not allowed or no solution can be found; (Bakker et al., 1993; Felfernig et al., 2004)) or redundant constraints (both also known as anomalies), which are not needed to express the domain knowledge in a complete fashion (Dechter and Dechter, 1987; Fahad and Qadir, 2008; Levy and Sagiv, 1992; Liberatore, 2005; Piette, 2008; Sabin and Freuder, 1999). In this chapter we focus on situations where users are defining redundant constraints that, when deleted from the constraint set, do not change the semantics of the remaining constraints. This might happen for performance reasons or due to the fact that knowledge engineers are not aware of the redundancy. We focus on the latter situation.
More formally, redundancy can be described as follows: if ![]() is a set of constraints and one constraint
is a set of constraints and one constraint ![]() is redundant, then
is redundant, then ![]() is inconsistent. In this context,
is inconsistent. In this context, ![]() is the negation1 of C: if
is the negation1 of C: if ![]() then
then ![]() .
.
Redundancy elimination in knowledge bases is a topic extensively investigated by AI research. Redundant constraints play a role, for example, in the development and maintenance of configuration knowledge bases (Sabin and Freuder, 1999). The authors introduce concepts for the detection of redundant constraints in conditional constraint satisfaction problems (CCSPs). The approach is based on the idea of analyzing the solution space of the given problem (on the level of individual solutions) in order to detect different types of redundant constraints. Piette (2008) provides a discussion of the role of redundancy elimination in SAT solving. The author introduces an (incomplete) algorithm for the elimination of redundant clauses and show its applicability on the basis of an empirical study. The role of redundancies in ontology development is analyzed by Fahad and Qadir (2008). The authors point out the importance of redundancy elimination and discuss typical modeling errors that occur during ontology development and maintenance. Grimm and Wissmann (2011) introduce algorithms for redundancy elimination in OWL ontologies. The authors propose an algorithm that computes redundant axioms by exploiting prior knowledge of the dispensibility of axioms. Levy and Sagiv (1992) analyze two types of redundancies in Datalog programs. First, they interpret redundancy in terms of reachability (i.e., rules and predicates are eliminated that are not part of any derivation tree). Second, redundancy is defined on the basis of the concepts ofminimal derivation trees, which do not include any pair of identical atoms where one is the predecessor of the other one. The redundancy detection algorithm introduced by Chmeiss et al. (2008) corresponds to the SEQUENTIAL algorithm discussed in this chapter. The work of Belov et al. (2012) is in the line of the COREDIAG algorithm originially introduced by Felfernig et al. (2011) in the sense of applying the idea of subformula checking to the identification of redundant clauses (e.g., in SAT solving).
All the mentioned approaches focus on the identification of redundant constraints in centralized scenarios where one or a few knowledge engineers are interested in identifying redundant constraints. In such scenarios it is assumed that only a small subset of the given constraints is redundant (this assumption is also denoted as low redundancy assumption; Grimm and Wissmann, 2011). In this chapter we go one step further and propose an algorithm that is especially useful in distributed knowledge engineering scenarios where we can expect a larger number of redundant constraints due to the fact that different contributors add constraints that are related to the same topic (see, e.g., Chklovski and Gil, 2005; Richardson and Domingos, 2003). We denote the assumption of larger sets of redundant constraints the high redundancy assumption. For example, we envision a scenario where a large number of users propose constraints to be applied by a constraint-based configuration or recommendation engine (Felfernig and Burke, 2008) and the task of an underlying algorithm is to identify minimal sets of constraints that retain the semantics of the original constraint set. We denote such constraint sets as minimal cores. Note that the following discussions are based on the assumption of consistent constraint sets. Methods for consistency restoration are discussed in Bakker et al. (1993), Felfernig et al. (2004, 2012), Friedrich and Shchekotykhin (2005). Also refer to Felfernig et al. (2014)2 and Friedrich et al. (2014).3
The major contributions of this chapter are the following. First, we introduce the algorithms SEQUENTIAL and COREDIAG which allow the determination of redundant constraints. COREDIAG is especially applicable in the context of distributed (community-based) knowledge engineering scenarios whereas SEQUENTIAL should be applied in “standalone” scenarios where the redundancy degree of knowledge bases is rather low. Second, we compare the performance of SEQUENTIAL and COREDIAG using a financial service knowledge base.
The remainder of this chapter is organized as follows. In Section 12.2 we introduce an example configuration knowledge base from the automotive domain. In Section 12.3 we introduce a basic algorithm for the determination of redundant constraints in centralized settings (SEQUENTIAL). In Section 12.4 we introduce the COREDIAG algorithm. Thereafter we report the results of a performance evaluation (Section 12.5). Section 12.6 concludes the chapter.
12.2 An Example Configuration Knowledge Base
For illustration purposes we use the following car configuration task thoughout this chapter.4 The variable type represents the type of the car, pdc is the park distance control feature, fuel represents the average fuel consumption per 100 kilometers, a skibag allows convenient ski stowage inside the car, and 4-wheel represents the gear type (4-wheel supported or not supported). These variables represent the possible combinations of customer requirements. The configuration knowledge base ![]() defines additional restrictions on the set of possible customer requirements
defines additional restrictions on the set of possible customer requirements ![]() .5
.5
• ![]()
• ![]()
![]()
![]()
![]()
![]()
• ![]()
![]()
![]()
![]()
![]()
![]()
• ![]()
![]()
![]()
![]()
![]()
![]()
A configuration (see Hotz et al., 20146) for our example configuration task would be ![]() {4-wheel = no, fuel = 4l, type = city, skibag = no, pdc = yes}.
{4-wheel = no, fuel = 4l, type = city, skibag = no, pdc = yes}.
12.3 Determining Redundant Constraints
Let us now consider a simple adaptation of the original set of constraints ![]() , which we denote with
, which we denote with ![]() .
. ![]() includes an additional constraint
includes an additional constraint ![]() , which has been added by a knowledge engineer.
, which has been added by a knowledge engineer.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
It is obvious that ![]() is redundant since it does not further restrict the solution space defined by
is redundant since it does not further restrict the solution space defined by ![]() . In order to discuss constraint redundancy on a more formal level, we introduce the following definitions.
. In order to discuss constraint redundancy on a more formal level, we introduce the following definitions.
Definition
Redundant Constraint
Let ![]() be a constraint of the configuration knowledge base
be a constraint of the configuration knowledge base ![]() .
. ![]() is called redundant iff
is called redundant iff ![]() . If this condition is not fulfilled,
. If this condition is not fulfilled, ![]() is said to be nonredundant. Redundancy can also be analyzed by checking
is said to be nonredundant. Redundancy can also be analyzed by checking ![]() for consistency. If consistency is given,
for consistency. If consistency is given, ![]() is nonredundant.
is nonredundant.
This definition is based on the definition of Dechter and Dechter (1987). Iterating over each constraint of ![]() , executing the nonredundancy check
, executing the nonredundancy check ![]() and deleting redundant constraints from
and deleting redundant constraints from ![]() results in a set of nonredundant constraints (theminimal core). If the nonredundancy check fails (no solution can be found), the constraint
results in a set of nonredundant constraints (theminimal core). If the nonredundancy check fails (no solution can be found), the constraint ![]() is redundant and can be deleted from
is redundant and can be deleted from ![]() . Otherwise,
. Otherwise, ![]() is nonredundant.
is nonredundant.
Definition
Minimal Core
Let ![]() be a configuration knowledge base.
be a configuration knowledge base. ![]() is denoted as minimal core iff
is denoted as minimal core iff ![]() is consistent. Obviously,
is consistent. Obviously, ![]() .
.
The principle of the following algorithm (SEQUENTIAL - Algorithm 12.1) is often used for determining such redundancies (see, e.g., Boufkhad and Roussel, 2000; Chmeiss et al., 2008; Fourdrinoy et al., 2007; Grimm and Wissmann, 2011; Piette, 2008).
Algorithm 12.1
SEQUENTIAL ![]()

The approach of SEQUENTIAL is straightforward (see, e.g., Boufkhad and Roussel, 2000; Chmeiss et al., 2008; Fourdrinoy et al., 2007; Grimm and Wissmann, 2011; Piette, 2008): each individual constraint ![]() is evaluated with regard to redundancy by checking whether
is evaluated with regard to redundancy by checking whether ![]() is still inconsistent with
is still inconsistent with ![]() . Instead of checking the inconsistency of
. Instead of checking the inconsistency of ![]() , SEQUENTIAL systematically reduces the number of constraints to be checked in
, SEQUENTIAL systematically reduces the number of constraints to be checked in ![]() . Given a configuration knowledge base
. Given a configuration knowledge base ![]() and its complement
and its complement ![]() , the (in)consistency check of
, the (in)consistency check of ![]() can be reduced to the inconsistency check of
can be reduced to the inconsistency check of ![]() where
where ![]() . If we assume that
. If we assume that ![]() , and
, and ![]() then the consistency check of
then the consistency check of ![]() can be reduced to
can be reduced to ![]() . In the SEQUENTIAL algorithm this property is exploited correspondingly.
. In the SEQUENTIAL algorithm this property is exploited correspondingly.
If ![]() is inconsistent,
is inconsistent, ![]() can be considered redundant. If
can be considered redundant. If ![]() is consistent with
is consistent with ![]() is a nonredundant constraint since its deletion induces consistency with
is a nonredundant constraint since its deletion induces consistency with ![]() . Applying the algorithm SEQUENTIAL to our example
. Applying the algorithm SEQUENTIAL to our example ![]() results in
results in ![]() =
= ![]() since
since ![]() is inconsistent and no further constraint
is inconsistent and no further constraint ![]() can be deleted from
can be deleted from ![]() such that
such that ![]() is still inconsistent. Table 12.1 shows an execution trace of the SEQUENTIAL redundancy detection algorithm on basis of our (redundant) example configuration knowledge base
is still inconsistent. Table 12.1 shows an execution trace of the SEQUENTIAL redundancy detection algorithm on basis of our (redundant) example configuration knowledge base ![]() .
.
Table 12.1
Example execution trace of SEQUENTIAL. The set of redundant constraints is ![]() .
.

The problem of checking whether a given constraint can be inferred from the remaining part of a constraint set has shown to be Co-NP-complete in the general case (Piette, 2008). There exist alternative algorithms that have a better runtime performance compared to SEQUENTIAL in situations with a large amount of redundant constraints in ![]() . Large amounts of redundant constraints typically occur in distributed knowledge engineering scenarios where a large number of users specify rules that in the following have to be aggregated into one consistent constraint set (see, e.g., Chklovski and Gil, 2005).
. Large amounts of redundant constraints typically occur in distributed knowledge engineering scenarios where a large number of users specify rules that in the following have to be aggregated into one consistent constraint set (see, e.g., Chklovski and Gil, 2005).
In the following section we introduce the COREDIAG algorithm, which is a valuable alternative to SEQUENTIAL in situations with a large number of redundant constraints. After having introduced COREDIAG we will analyze the performance of both algorithms (SEQUENTIAL and COREDIAG) on the basis of a financial services knowledge base (Section 12.5).
12.4 CoreDiag
The COREDIAG algorithm (together with CORED; Felfernig et al., 2011) is based on the principle of divide-and-conquer: whenever a set ![]() , which is a subset of
, which is a subset of ![]() , is inconsistent with
, is inconsistent with ![]() , it is or contains a minimal core (i.e., a set of constraints that preserve the semantics of
, it is or contains a minimal core (i.e., a set of constraints that preserve the semantics of ![]() ). In our implementation, CORED is responsible for determining such minimal cores, COREDIAG returns the complement of a minimal core, which is a maximal set of redundant constraints in
). In our implementation, CORED is responsible for determining such minimal cores, COREDIAG returns the complement of a minimal core, which is a maximal set of redundant constraints in ![]() . CORED is based on the principle of QUICKXPLAIN (seeFelfernig et al., 2014);7 as a consequence a minimal core (minimal set of constraints that preserve the semantics of
. CORED is based on the principle of QUICKXPLAIN (seeFelfernig et al., 2014);7 as a consequence a minimal core (minimal set of constraints that preserve the semantics of ![]() ) can be interpreted as a minimal conflict (i.e., a minimal set of constraints that are inconsistent with
) can be interpreted as a minimal conflict (i.e., a minimal set of constraints that are inconsistent with ![]() ).
).
CORED allows the determination of preferred minimal cores since the algorithm is based on the assumption of a strict lexicographical ordering of the constraints in ![]() . On an informal level, a preferred minimal core can be characterized as follows: if we have different options for choosing a minimal core, we would select the one with the most agreed-upon constraints. For more details on the role of strict lexicographical orderings of constraints refer to the work of Junker (2004) and Felfernig et al. (2012).
. On an informal level, a preferred minimal core can be characterized as follows: if we have different options for choosing a minimal core, we would select the one with the most agreed-upon constraints. For more details on the role of strict lexicographical orderings of constraints refer to the work of Junker (2004) and Felfernig et al. (2012).
The COREDIAG algorithm (see Algorithm 12.2) generates ![]() from
from ![]() . It then activates CORED (see Algorithm 12.3), which determines a minimal core on the basis of a divide-and-conquer strategy that divides the constraints in
. It then activates CORED (see Algorithm 12.3), which determines a minimal core on the basis of a divide-and-conquer strategy that divides the constraints in ![]() into two subsets (
into two subsets (![]() and
and ![]() ), with the goal to figure out whether one of those subsets already contains a minimal core. If
), with the goal to figure out whether one of those subsets already contains a minimal core. If ![]() contains a minimal core,
contains a minimal core, ![]() is not further taken into account. If
is not further taken into account. If ![]() contains only one element (
contains only one element (![]() ) and
) and ![]() is still consistent, then
is still consistent, then ![]() is part of the minimal core.
is part of the minimal core.
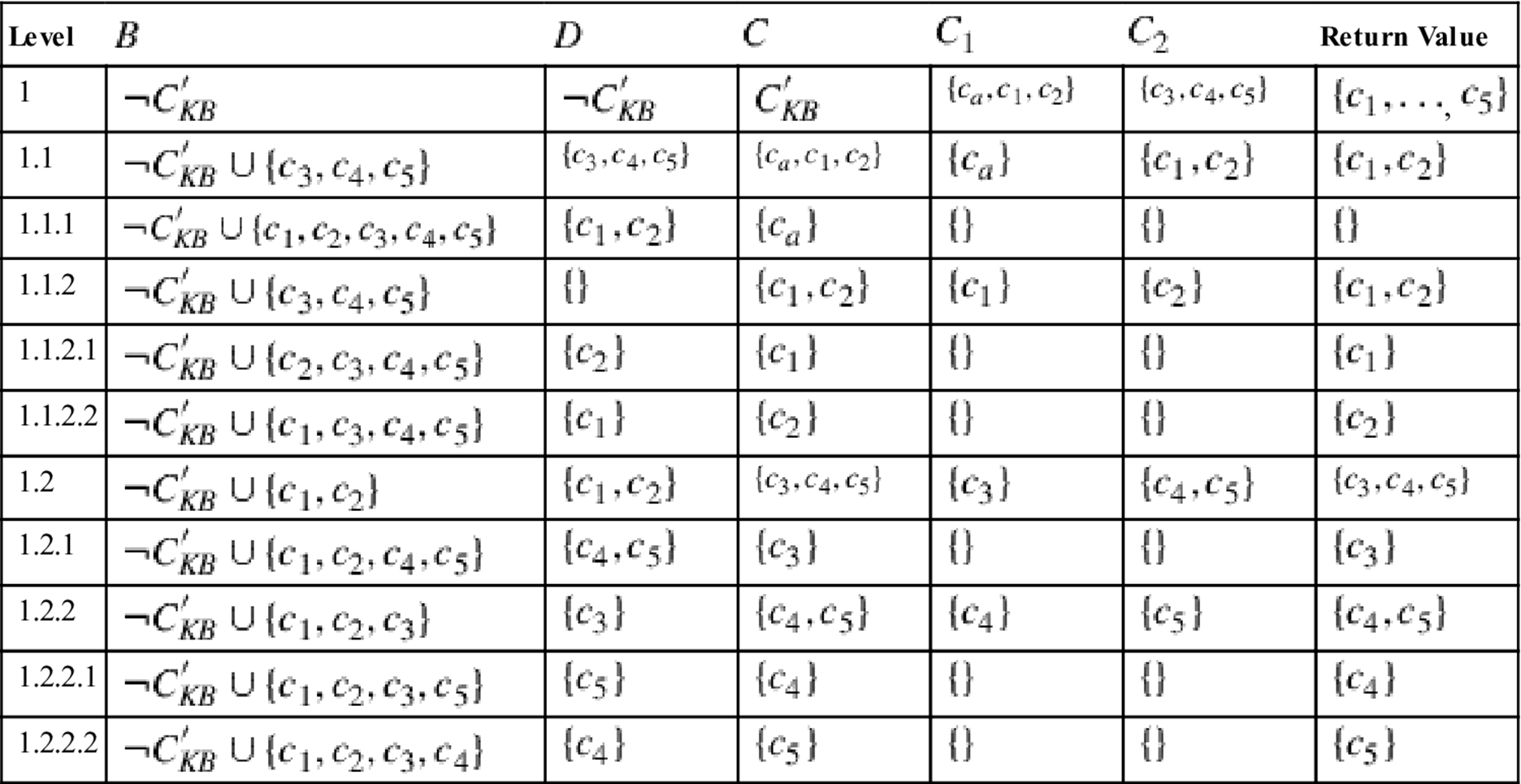
Table 12.2 shows an execution trace of the COREDIAG redundancy detection algorithm on basis of our (redundant) example configuration knowledge base ![]() . In this context, the recursive function CORED is responsible for determining a minimal core (if one exists). The basic approach of CORED is to identify a minimal conflict set CS for
. In this context, the recursive function CORED is responsible for determining a minimal core (if one exists). The basic approach of CORED is to identify a minimal conflict set CS for ![]() such that
such that ![]() is inconsistent. The identified conflict set represents the minimal core and
is inconsistent. The identified conflict set represents the minimal core and ![]() the set of redundant constraints.
the set of redundant constraints.
Algorithm 12.2
COREDIAG ![]()
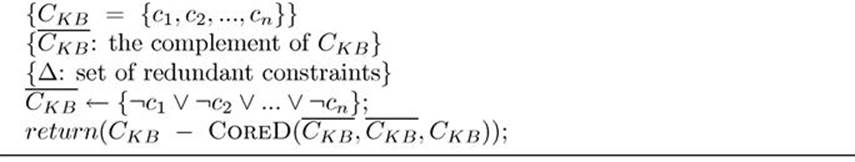
Algorithm 12.3
CORED![]()

Table 12.2
Example execution trace of COREDIAG.
12.5 Evaluation
We now compare the performance of COREDIAG with the SEQUENTIAL algorithm discussed in Section 12.3. The worst case complexity (and best case complexity) of SEQUENTIAL in terms of the number of needed consistency checks is ![]() (the number of constraints in
(the number of constraints in ![]() ). Worst case and best case complexity are identical since SEQUENTIAL checks the redundancy of each individual constraint
). Worst case and best case complexity are identical since SEQUENTIAL checks the redundancy of each individual constraint ![]() with respect to
with respect to ![]() . In contrast, the worst case complexity of COREDIAG depends on the number of redundant constraints in
. In contrast, the worst case complexity of COREDIAG depends on the number of redundant constraints in ![]() . The worst case complexity of COREDIAG in terms of the number of needed consistency checks is
. The worst case complexity of COREDIAG in terms of the number of needed consistency checks is ![]() , where
, where ![]() is the number of constraints in
is the number of constraints in ![]() and
and ![]() is the minimal core size. The best case complexity in terms of the number of needed consistency checks can be achieved if all constraint elements of the minimal core are positioned in one branch of the CORED search tree:
is the minimal core size. The best case complexity in terms of the number of needed consistency checks can be achieved if all constraint elements of the minimal core are positioned in one branch of the CORED search tree: ![]() . Consequently, the performance of COREDIAG heavily relies on the number of constraints contained in the minimal core (the lower the number of constraints in the minimal core, the better the performance of COREDIAG).
. Consequently, the performance of COREDIAG heavily relies on the number of constraints contained in the minimal core (the lower the number of constraints in the minimal core, the better the performance of COREDIAG).
Figure 12.1 shows a comparison of the performance of SEQUENTIAL and COREDIAG with regard to a financial service knowledge base (Felfernig et al., 2011). In addition to the original version (redundancy rate = ∼0 –10%) three knowledge bases with the redundancy rates 50%, 75%, and 87.5% were generated. For example, a knowledge base with a redundancy rate of 50% was generated by simply duplicating each constraint of the original knowledge base. Starting with a redundancy rate of 50% we can observe a transition in the runtime performance (COREDIAG starts to perform better than SEQUENTIAL) due to the increased number of redundant constraints.
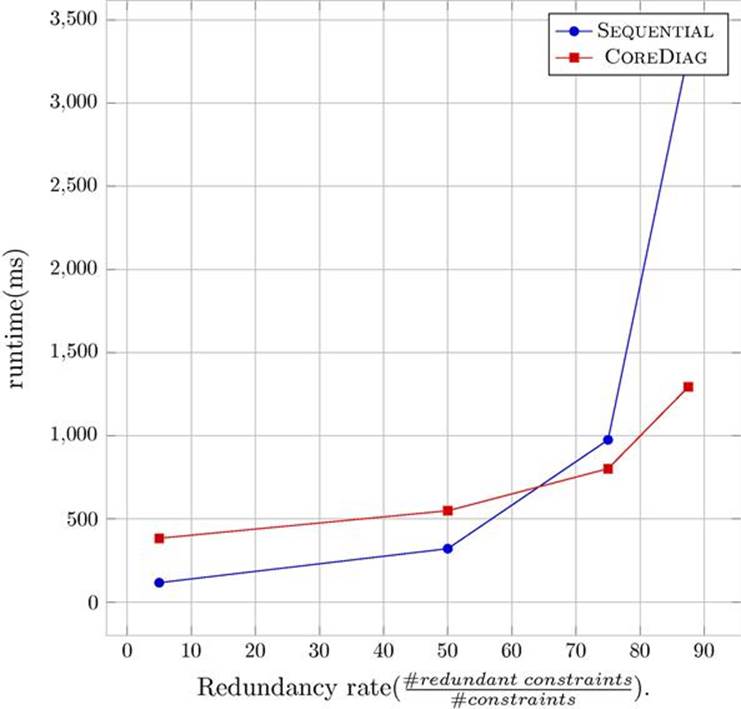
FIGURE 12.1 Performance of SEQUENTIAL and COREDIAG for a financial services knowledge base (see Felfernig et al. 2011).
12.6 Conclusion
Intelligent support of redundancy detection is a building block of intuitive knowledge engineering support. In this chapter we have discussed two algorithms that can be applied for the identification of minimal cores (i.e., minimal sets of constraints that preserve the semantics of the original knowledge base). The SEQUENTIAL algorithm can be applied in settings where the number of redundant constraints in the knowledge base is low. The second algorithm (COREDIAG) is more efficient but restricted in its application to knowledge bases that contain a large number of redundant constraints. For an in-depth analysis of theoretical issues related to the identification of redundancies refer to Liberatore (2005, 2008a,b).
References
1. Bakker R, Dikker F, Tempelman F, Wogmim P. Diagnosing and solving over-determined constraint satisfaction problems. In: 13th International Joint Conference on Artificial Intelligence, Chambery, France. 1993:276–281.
2. Belov A, Janota M, Lynce I, Marques-Silva J. On computing minimal equivalent subformulas. In: Principles and Practices of Constraint Programming (CP 2012) No 7514 in Lecture Notes in Computer Science. Québec City, QC, Canada: Springer; 2012;158–174.
3. Boufkhad Y, Roussel O. Redundancy in random SAT formulas. In: 17th National Conference on Artificial Intelligence (AAAI-00), Austin, Texas. 2000:273–278.
4. Chklovski T, Gil Y. An analysis of knowledge collected from volunteer contributors. In: 20th National Conference on Artificial Intelligence (AAAI-05), Pittsburg, Pennsylvania. 2005:564–571.
5. Chmeiss A, Krawczyk V, Sais L. Redundancy in CSPs. In: Ghallab M, Spyropoulos CD, Fakotakis N, Avouris NM, eds. 18th European Conference on Artificial Intelligence (ECAI 2008), Patras, Greece. 2008;907–908.
6. Dechter A, Dechter R. Removing redundancies in constraint networks. In: 6th National Conference on Artificial Intelligence (AAAI-87), Seattle, Washington. 1987:105–109.
7. Fahad M, Qadir M. A framework for ontology evaluation. In: Supplementary Proceedings of the 16th International Conference on Conceptual Structures (ICCS 2008), Toulouse, France. 2008;149–158.
8. Felfernig A, Burke R. Constraint-based recommender systems: Technologies and research issues. In: ACM International Conference on Electronic Commerce (ICEC08), Innsbruck, Austria. 2008:17–26.
9. Felfernig A, Friedrich G, Jannach D, Stumptner M. Consistency-based diagnosis of configuration knowledge bases. Artificial Intelligence. 2004;152(2):213–234.
10. Felfernig A, Zehentner C, Blazek P. CoreDiag: Eliminating redundancy in constraint sets. In: 22nd International Workshop on Principles of Diagnosis (DX’2011), Murnau, Germany. 2011;219–224.
11. Felfernig A, Schubert M, Zehentner C. An efficient diagnosis algorithm for inconsistent constraint sets. Artificial Intelligence for Engineering Design, Analysis and Manufacturing (AI EDAM). 2012;26(1):53–62.
12. Felfernig A, Reiterer S, Reinfrank F, Ninaus G, Jeran M. Conflict detection and diagnosis in configuration. In: Felfernig A, Hotz L, Bagley C, Tiihonen J, eds. Knowledge-based Configuration – From Research to Business Cases. Waltham, MA: Morgan Kaufmann Publishers; 2014:73–87. (Chapter 7).
13. Fourdrinoy O, Grégoire E, Mazure B, Saïs L. Eliminating redundant clauses in SAT instances. In: 4th International Conference on Integration of AI and OR Techniques in Constraint Programming for Combinatorial Optimization Problems No 4510 in Lecture Notes in Computer Science. Brussels, Belgium: Springer; 2007:71–83.
14. Friedrich G, Shchekotykhin K. A general diagnosis method for ontologies. In: 4th International Semantic Web Conference (ISWC05) No 3729 in Lecture Notes in Computer Science. Galway, Ireland: Springer; 2005:232–246.
15. Friedrich G, Jannach D, Stumptner M, Zanker M. Knowledge engineering for configuration systems. In: Felfernig A, Hotz L, Bagley C, Tiihonen J, eds. Knowledge-based Configuration – From Research to Business Cases. Waltham, MA: Morgan Kaufmann Publishers; 2014:139–155. (Chapter 11).
16. Grimm S, Wissmann J. Elimination of redundancy in ontologies. In: The Semantic Web: Research and Applications, 8th Extended Semantic Web Conference (ESWC 2011) No 6643 in Lecture Notes in Computer Science. Heraklion, Greece: Springer; 2011;260–274.
17. Hotz L, Felfernig A, Stumptner M, Ryabokon A, Bagley C, Wolter K. Configuration knowledge representation and reasoning. In: Felfernig A, Hotz L, Bagley C, Tiihonen J, eds. Knowledge-based Configuration – From Research to Business Cases. Waltham, MA: Morgan Kaufman Publishers; 2014:41–72. (Chapter 6).
18. Junker U. QUICKXPLAIN: Preferred explanations and relaxations for over-constrained problems. In: McGuinness DL, Ferguson G, eds. 19th International Conference on Artifical Intelligence (AAAI’04). AAAI Press 2004:167–172.
19. Levy A, Sagiv Y. Constraints and redundancy in Datalog. In: 11th Symposium on Principles of database systems, San Diego, California. 1992:67–80.
20. Liberatore P. Redundancy in logic I: CNF propositial formulae. Artificial Intelligence. 2005;163(2):203–232.
21. Liberatore P. Redundancy in logic II: 2CNF and horn propositional formulae. Artificial Intelligence. 2008a;172(2–3):265–299.
22. Liberatore P. Redundancy in logic III: Non-monotonic reasoning. Artificial Intelligence. 2008b;172(11):1317–1359.
23. Piette C. Let the solver deal with redundancy. In: 20th IEEE International Conference on Tools with Artificial Intelligence (ICTAI’08), Dayton, Ohio. 2008:67–73.
24. Richardson M, Domingos P. Building large knowledge bases by mass collaboration. In: 2nd International Conference on Knowledge Capture (K-CAP 2003), Sanibel Island, Florida. 2003;129–137.
25. Sabin, M., Freuder, E. 1999. Detecting and resolving inconsistency and redundancy in conditional constraint satisfaction problems. AAAI 1999 Workshop on Configuration (AAAI Technical Report WS-99-05), Orlando, Florida, 90–94.
1We denote the negation of ![]() also the complement of C.
also the complement of C.
2Chapter 7.
3Chapter 11.
4A configuration task consists of a configuration knowledge base (![]() ) and a set of customer requirements (
) and a set of customer requirements (![]() ); a formal definition can be found in Chapter 6.
); a formal definition can be found in Chapter 6.
5Note that the presented concepts are as well applicable to other types of knowledge representations such as SAT or description logics.
6Chapter 6.
7Chapter 7.